基于故障指示器的单相接地故障区段定位方法的研究
2021-03-19高宏宇王岩乔建
高宏宇,王岩,乔建
(1. 东北电力大学 电气工程学院,吉林 吉林 132012;2.吉林省电力有限公司吉林供电公司,吉林 吉林 132012)
0 引 言
故障指示器在整个系统中所扮演的角色是最基础的控制采集单元的角色。这个测控单元的性能指标主要包括数据传输可靠性、数据采集可靠性和数据类型[1]。这些指标直接对于配网自动化有着巨大的影响。故障指示器具有很多功能,但在故障定位方面,主要用到的功能包括四个方面:远程通信、遥测、遥信和遥控。首先是遥信功能,这种功能实际上就是对各种信息的采集,如元件电源是否正常、通信是不是流畅以及开关位置等[2-5];对于遥测功能,主要完成的是对于正常运行以及故障时各种电量信号的采集;对于遥控功能,即从远方进行控制,因此要求可以接受从远处控制中心传来的命令,从而在远方就能控制启动以及开关的闭合;对于远程通信功能,在这个领域内就要求其能够对故障前后电网中的一些电量信息进行上传和监控[6-8]。故障指示器的广泛使用为配网单向接地故障定位带来了很大的方便。本文以故障指示器为基础,结合零序电流能量和矩阵算法实现了故障的准确定位。
1 基于故障指示器配网自动化系统的特点
图1为在配电网中装有故障指示器的线路,这些故障指示器分别安装在固定距离的开关柱上,对于这些开关柱上的电量如电流、电压、功率方向和各个开关的状态等都有信息采集功能。在采集完这些信息后,会将信息通过通信网络上传到自动控制主站。
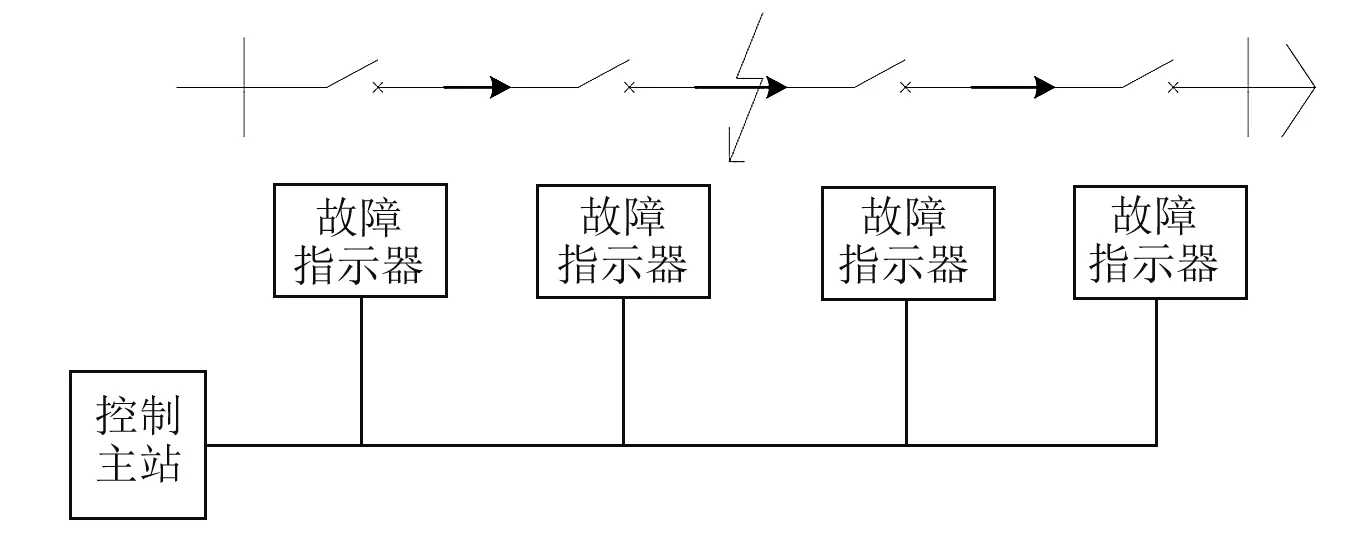
图1 安装故障指示器的配电线路
除此之外,还可以经由通信网络接受到主站传来的指令,进行一些倒闸等的操作。综上所述,当配电网发生故障的时候,这些故障信息可以利用故障指示器进行采集,再将采集到的信息经通信系统上传至控制主站,然后通过主站的分析,确定出发生故障的区段,最后通过遥控倒闸的操作实现故障隔离。
2 基于故障指示器故障定位的矩阵算法
以故障指示器为基础,在馈线自动化技术中,应用于故障区段定位中的的矩阵算法就是将故障之后以及故障之前的信息通过故障指示器的通信通道,上传到主站的控制中心。之后,再通过控制中心对这些信息进行矩阵运算,从而得到故障区间的过程。在故障区段定位应用的算法中,使用的矩阵算法是通用算法,其实现过程如下。
起初,对于任何一个配电网系统,都可以针对这个系统的拓扑结构形成一个矩阵,这个矩阵称之为网络描述矩阵D。如果这个配电网的系统发生了故障,由该系统中各个节点处的故障指示器检测到的信息,将信息向主站上传,形成一个新矩阵,即故障信息矩阵G。之后将前面得到的两个矩阵进行乘法处理,这样就可以得到一个新的矩阵。但通过这个矩阵还不能直接找出故障区间,对于这个矩阵进行所谓的格式化处理之后,就可以得到进行故障区间判定时要用的矩阵,称之为故障判断矩阵P。对这个得到的矩阵P内元素进行分析,就可以知道发生故障的位置在哪两个节点之间。
下面对于该算法的具体实现过程进行详细的说明。首先找到一个具有节点的网络,如图2所示。

图2 简单的馈线网络
对该网络进行编号,参与编号的节点就是网络范围内的断路器以及开关柱上的故障指示器。图2所示的网络有节点数6个,因此这个网络可以列出一个6×6阶的方阵。如果节点i以及节点j中间存在线路上的直接联系,也就是说这两个点是所谓的临近点,这个时候对于在i行i列或是在j行j列的数值设定成1,之后把这个矩阵的其他的数值设定成0。这样就形成了前面所说的可以反映网络的拓扑结构的矩阵,即网络描述矩阵D。

(1)
利用相似的形成方法,这个网络里形成的故障信息矩阵G也同样为6×6阶的矩阵。本文使用对于故障的判定标准为:在各个节点的故障指示器处预定一个故障信息比较值,这里取零序电流能量。故障出现之后,如果说检测到节点i上的故障指示器的零序电流能量值的计算值大于这个使用的整定值,那么就会把所要形成的这个矩阵的i行i列的元素设定为0。反之把位于i行i列的元素设定为1。对于其他元素,都将数值设定为0。根据前面所分析的网络的矩阵形成方式,可以结合故障出现的位置,得到故障信息矩阵,即:

(2)
在前面的两个方阵都形成之后,可以把这两个方阵作乘法处理。之后对于这个运算结果进行所谓的规格化。通过上面的运算之后就得到所需要的矩阵,即最终的方阵P。
P=g(D×G)
(3)
式中:D为网络描述矩阵;G为故障信息矩阵。在这里,要具体的介绍一下规格化的操作,该方法的描述如下:对于前面所列出的方阵D中各值dmj,dnj,…,dkj=1。由于矩阵G中的固定一个值gjj也为1,并且gmm,gnn,…,gkk这些值里面为0的数字大于等于2,因此把D×G矩阵里面的j行j列的元素进行了格式化运算,也就是把在j行j列的所有元素设定为0。如果有些元素不符合上面的两个条件,则这些元素的值不发生变化。由上面的网络图的具体的故障区段情况,可以得到如下矩阵,即故障判断矩阵P。
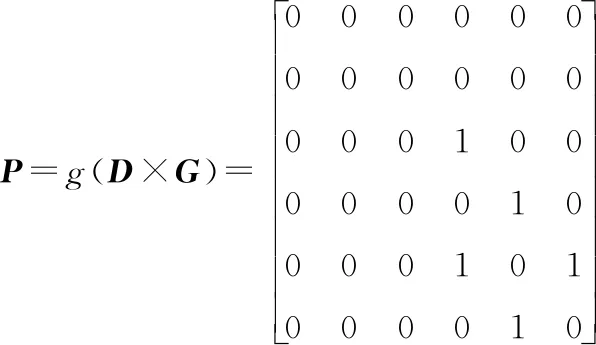
(4)
之后就可以判定发生故障时故障点所位于整条线路的区间了。具体方法可以由前面给出的故障判断矩阵看出来,在矩阵P中,如果对于矩阵P中某个元素pij∧pji=1,那么位于节点i以及节点j之间的这个区间发生了故障。对于上面例子可以由P矩阵看出来对于元素p34∧p43=1,则故障位于节点3以及节点4之间。
3 仿真验证
该系统为中性点经消弧线圈接地系统,电压等级为6 kV,这里对于仿真过程中线路参数的设定如下:R1=0.012 64 Ω/km、R0=0.375 4 Ω/km;L1=0.935 6 mH/km,L0=4.124 2 mH/km;C1=12.81 μF/km,C0=7.749 μF/km。对于消弧线圈,在这里设置L=1.5 H、R=30 Ω。对于线路负载,这里使用的是三相串联RLC模块,将系统的各个有功负荷设置为10 MW。
模型中共3条6 kV输电线路,均采用π型等效电路模型,其中故障线路为线路3。在故障线路上设置四个故障指示器,故障点位于故障指示器2和故障指示器3之间。将三相电压电流测量模块作为故障指示器,从而实现对故障点前后零序电流信号的测量。将故障指示器检测到的A、B、C三相线路的故障电流引出,通过加法器相加,得到三倍的零序电流,进行仿真验证。
系统模型中,仿真系统运行时间为0.2 s,故障时刻0.045 s,当线路3出现某一相的故障时,检测到的系统发生接地的线路三倍零序电流值如图3所示。
图3中:第一个波形图为系统发生金属性接地时故障点前后故障指示器所检测到的三倍零序电流波形;第二个波形图为系统发生非金属性接地时,设置过渡电阻2 000 Ω,故障点前后故障指示器所检测到的三倍零序电流波形。当故障发生前系统中零序电流为零,在系统发生故障之后系统中开始出现零序电流,并且此时的零序电流中含有大量的奇次谐波。随着时间的推移谐波快速衰减,故障状态过渡到了稳态。由于故障发生在故障指示器2和故障指示器3之间,因此这里将故障指示器2与故障指示器3检测到的零序电流波形进行对比。很明显,当线路发生故障后,故障点前后故障指示器检测到的零序电流幅值具有十分明显的变化,且该方法同时适用于金属性接地与非金属性接地。
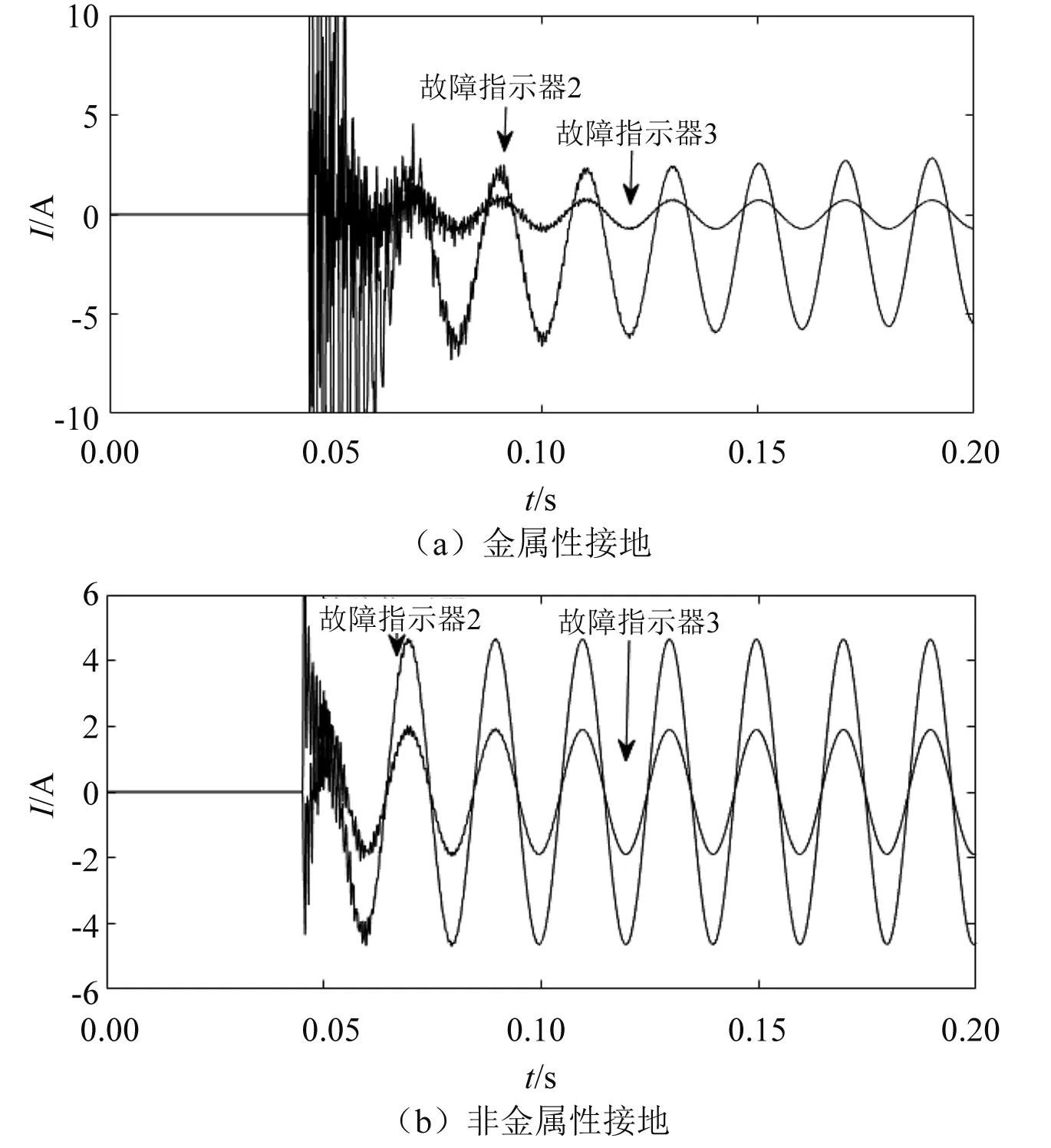
图3 系统发生单相接地短路故障零序电流波形图
对故障线路各个故障指示器检测到的零序电流进行采样分析,利用离散形式下的电流能量计算公式,得到各个监测点检测到的零序电流能量值。为验证该区段定位方法的有效性,将在故障距离和过渡电阻方面考虑不同种影响因素,并对影响因素进行仿真。
(1)当故障距离为3 km时,故障位置位于故障指示器1与故障指示器2之间,故障区段定位仿真结果如表1所示。
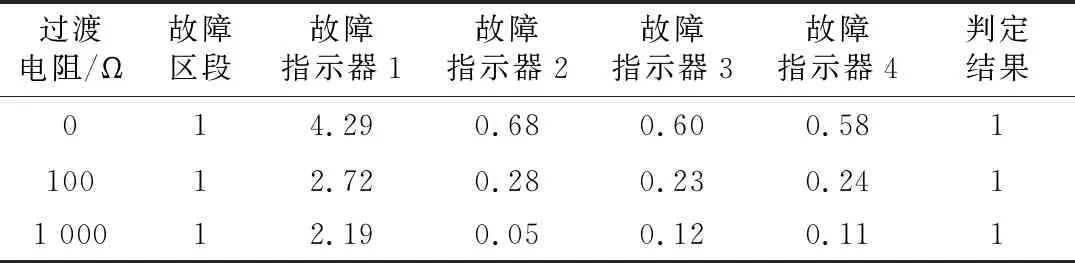
表1 故障区段定位仿真结果
(2)当故障距离为8 km时,故障位置在故障指示器2与故障指示器3之间,故障区段定位仿真结果如表2所示。

表2 故障区段定位仿真结果
(3)当故障距离为15 km时,故障位置在故障指示器3与故障指示器4之间,故障区段定位仿真结果如表3所示。
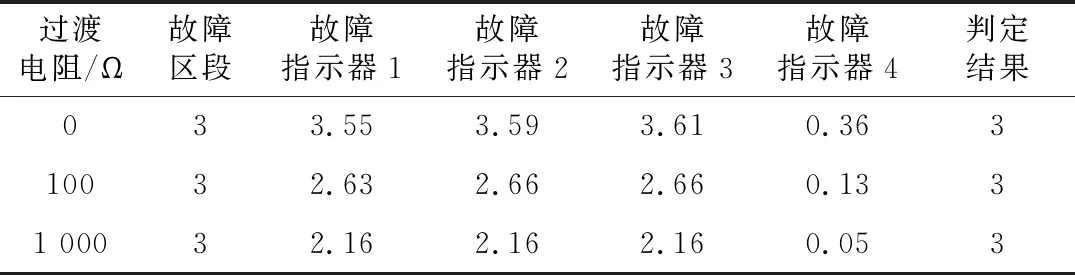
表3 故障区段定位仿真结果
4 结束语
通过以上分析可知,在基于故障指示器的区段定位方法中,以零序电流能量作为特征量,形成故障信息矩阵,可准确找到故障区段,且该方法不受故障距离的影响,仿真结果充分说明了该方法的有效性和实用性。
