基于Pushover分析的T型刚构桥易损位置确定

王平波 张潇

为快速确定T型刚构桥的易损位置，文章采用Pushover静力弹塑性分析方法，选择墩顶节点作为控制节点，集中荷载作为水平侧向力，控制节点的最大位移取0.1 m，分为100步逐级加载。分析结果表明：T型刚构桥的易损位置为墩底和墩顶，且墩底更容易发生破坏。同时，采用了OpenSees有限元软件，通过计算顺桥向地震动激励下各个截面曲率最大值，根据墩身方向的曲率包络图，验证Pushover分析结果的正确性。

Pushover分析; T型刚构桥; 塑性铰; 损伤位置

U448.23+1   A

[定稿日期]2021-03-18

[作者简介]王平波（1995～），男，硕士，主要从事桥梁损伤识别及健康监测研究。

确定损伤位置是桥梁损伤模式识别中非常重要的一步，弹塑性时程分析被认为是一种较为可靠的方法。但是由于其计算耗时，结果处理繁杂，并不能快速确定结构的易损位置。相比而言，Pushover分析方法具有简单、实用、计算效率高以及结果较为准确等特点，是一种具有较好应用前景的结构弹塑性地震响应分析方法[1]。

KrawinklerH等详细总结了Pushover分析方法的基本原理、实施步骤以及该方法的优缺点和适用范围[2]。Kilar V等应用pushover方法计算了9层框架结构的最大位移，并与弹塑性时程分析结果进行了对比，发现两者非常接近[3]。王东升等给出了一个利用Pushover分析方法评价桥梁抗震安全性的工程实例，并发现Pushover分析方法能够有效地评估桥梁结构的抗震性能[4]。潘龙等针对规则普通桥梁结构，提出了基于Pushover分析的桥梁地震损伤评估模型，该方法避免了非线性动力分析的繁琐，用简便的手段描述结构非线性特性，评价结构遭受不同地震烈度时的损伤程度[5]。王克海等采用pushover方法对一座6跨简支梁桥进行了抗震性能的分析计算，为静力弹塑性分析方法在桥梁工程中的应用提供了参考[6]。

上述学者主要采用Pushover分析来确定结构目标位移和判断结构的抗震承载力。但是采用Pushover分析来预测结构行为的还比较少，采用Pushover分析可以大致预测结构在地震作用下的行为，即预测结构从弹性—开裂—屈服—倒塌的全过程，模拟结构塑性铰出现的先后顺序和位置，找出结构的薄弱环节。

本文采用Pushover静力弹塑性分析方法，以快速确定T型刚构桥的易损位置。同时，结合OpenSees有限元软件，计算顺桥向地震动激励下各个截面曲率最大值，根据墩身方向的曲率包络图，验证Pushover分析结果的正确性。

1 Pushover分析方法

Pushover分析也叫静力弹塑性分析，其采用荷载控制或位移控制的方式，在加载过程中根据构件屈服程度而动态调整结构刚度，直至结构控制点达到目标位移或结构被推覆为止[7]。

1.1 基本原理

Pushover分析将复杂的动力弹塑性问题转化为简单的静力弹塑性问题[8]，试图用静力方法来近似反映结构的动力特性。其基本原理是：在结构上作用某种单调递增的侧向荷载，来模拟地震惯性力，使结构各部分逐步达到弹塑性状态，进而获得结构在侧向荷载作用下的弹塑性性能，并以此作为结构抗震性能评估的依据。

在给定水平侧向荷载时，对结构进行Pushover分析时平衡方程的增量形式为：

KΔu=ΔF+ΔFu（1）

式中：K表示结构的侧移刚度矩阵，Δu表示水平侧向位移的增量列向量，ΔF表示水平侧向力的增量列向量，ΔFu表示结构中不平衡力的列向量。

在进行Pushover分析时，有2种加载控制方式，即侧向位移控制和侧向力控制。当采用侧向位移控制时，增加侧向位移产生的侧向力增量可按式（1）计算。Pushover分析并没有很严密的理论推导，有两个基本假定，即：忽略高阶振型对结构的影响，结构的响应由基本振型控制;结构的变形由形状向量Φ表示，在加载过程中，结构的形状向量Φ保持不变。严格来说，该假定不完全准确，它忽略了高阶振型对结构的影响。但是，对于由基本振型控制的结构来说，Pushover分析方法能够很好的预测结构地震动力反应。

1.2 实施步骤

本文采用Pushover分析方法对结构进行行为分析，即预测结构在侧向荷载作用下，相关构件在各个阶段所处的状态，找出塑性铰在结构中出现的位置和顺序，相应的步骤如下：

（1）建立结构有限元模型;

（2）根据结构所用材料的本构关系，计算结构各单元的塑性铰特性;

（3）对结构进行静力分析，计算在初始荷载作用下的结构内力情况;

（4）选择控制节点和侧向力分布模式;

（5）根据所选的加载模式，对结构进行逐级加载，在结构中某一构件出现开裂或屈服后，对其刚度进行折减，在原有侧向荷载的基础上继续施加一定的侧向荷载，继续“Push”，直到结构中新的构件开裂或者屈服;

（6）不断重复步骤（5），直至控制节点达到目标位移或者结构倒塌。

2 应用实例

2.1 模型概况

2.1.1 桥型及布置

从桥梁地震损伤诊断出发，选择两跨T型预应力混凝土连续刚构桥结构，进行振动台模型的设计。主梁为对称布置，每跨4.6 m，总长9.2 m，桥墩高度为5 m。

2.1.2 主要材料

考慮到模型尺寸要求以及浇筑方便，承台、桥墩和主梁均采用C40细骨料混凝土;钢筋采用HRB335钢筋，箍筋直径8 mm，纵筋直径10 mm;钢筋混凝土容重ρ=2 600 kg/m3，钢筋混凝土部分包括桥墩承台以及主梁，共计20.13 t。

2.1.3 布置及构造

为方便配重以及实验加载过程中安全，主梁采用U型梁，配重块放在U型槽中。主梁宽度为75 cm，主梁长度为920 cm，肋板厚度为12 cm。梁高分为等高段和变高段，其中变高段采用二次抛物线。

桥墩采用空心墩，在墩底设置50 cm高的实心段。墩底实心段为46 cm×75 cm的矩形截面，空心段中空心部分为26×51 cm的矩形。在墩底和墩顶分别设置15 cm和8 cm的空心过渡段。

2.2 T型刚构桥的Pushover分析

2.2.1 有限元模型的建立

采用Midas/Civil建立T型剛构桥的有限元模型，图1所示。主梁划分了34个单元，桥墩划分了14个单元。约束条件与实验时保持一致，即墩底固结，主梁两端纵向放开，桥墩与主梁固结。

2.2.2 设定塑性铰特性值

在计算各单元的塑性铰特性值之前，要确定结构所用材料的本构关系，混凝土采用Mander本构模型，混凝土类型为无约束混凝土，并忽略混凝土的抗拉强度; HRB335钢筋采用双折线模型，钢筋屈服强度为335 MPa。

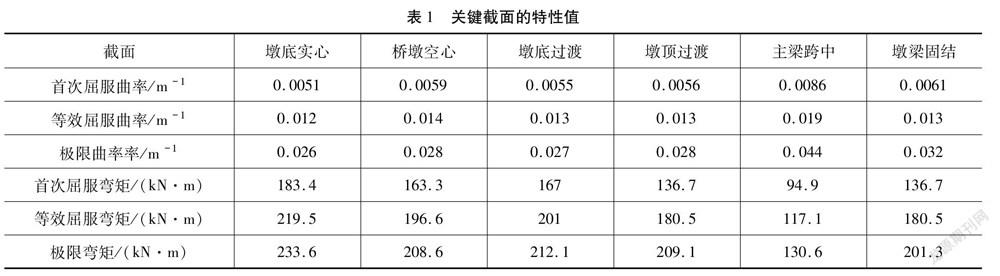
根据材料的本构关系，计算出T型刚构桥各单元截面的特性值，表1展示了几个关键截面的特性值。

2.3.3 选择控制节点对结构进行Pushover分析

在Pushover分析过程中，控制节点起着监控结构位移的作用，因此，控制节点的选择应当满足以下两个条件：①控制节点的位移应为结构的最大位移;②控制节点位移变化能够反映结构的受力特性。

水平侧向力的分布模式应当能够合理地反映出结构的惯性力分布[9]，目前在Pushover分析中常用的侧向荷载模式有均匀分布、倒三角分布、集中荷载分布及振型分布等。

考虑到初始荷载作用下结构的非线性，首先对结构进行静力分析，计算出结构在初始荷载作用下的结构内力。在对结构进行静力分析后，选择控制节点对结构进行逐级加载。本文选择墩顶节点作为控制节点，控制节点的最大位移暂取0.1 m;同时，为简化计算，水平侧向力采用集中荷载，分为100步逐级加载。

2.3 T型刚构桥的易损位置确定

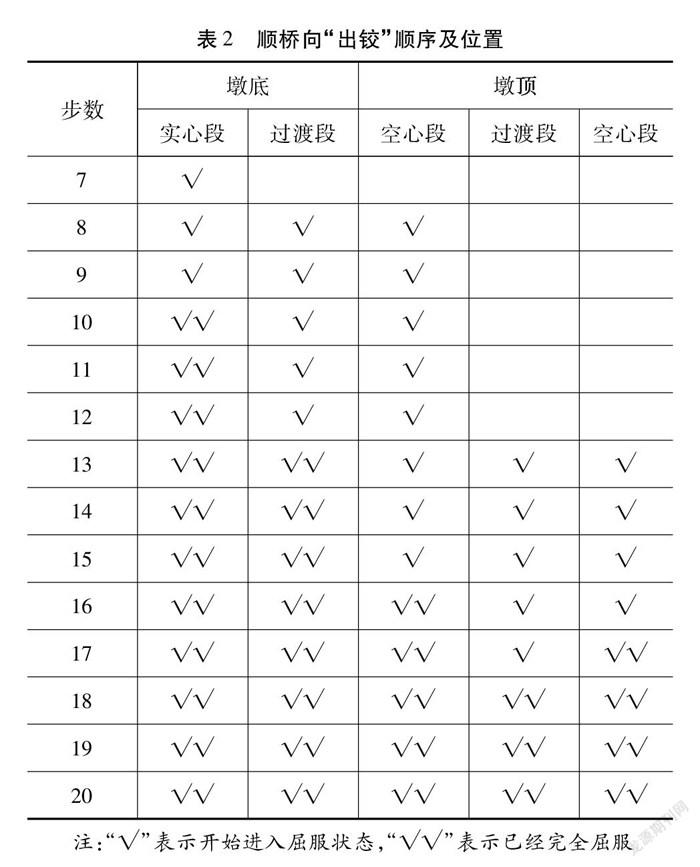
由于该T型刚构桥在顺桥向地震激励下的损伤模式更为丰富，故仅分析T型刚构桥顺桥向的易损位置。在Pushover分析完成后，可查看每一步“Push”过程中结构各单元所处的状态，T型刚构桥顺桥向“出铰”顺序及位置如表2所示。

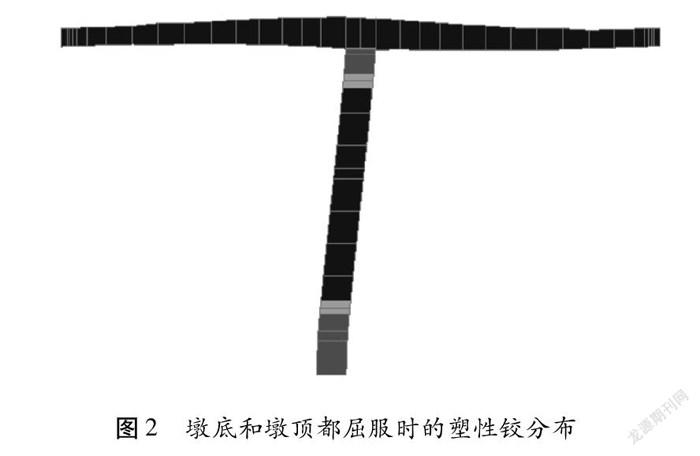
由表2可知，在第7步的时候，墩底实心段开始出现塑性铰，紧接着，墩底过渡段和墩底空心段也开始塑性铰。到了第13步，墩顶开始出现塑性铰，并在第18步的时候，墩底和墩顶均完全屈服。由此可以判定T型刚构桥的薄弱位置为墩底截面和墩顶截面。在第20步时，即在墩底和墩顶均已完全屈服时，结构的塑性铰分布如图2所示。

2.4 OpenSees对比分析

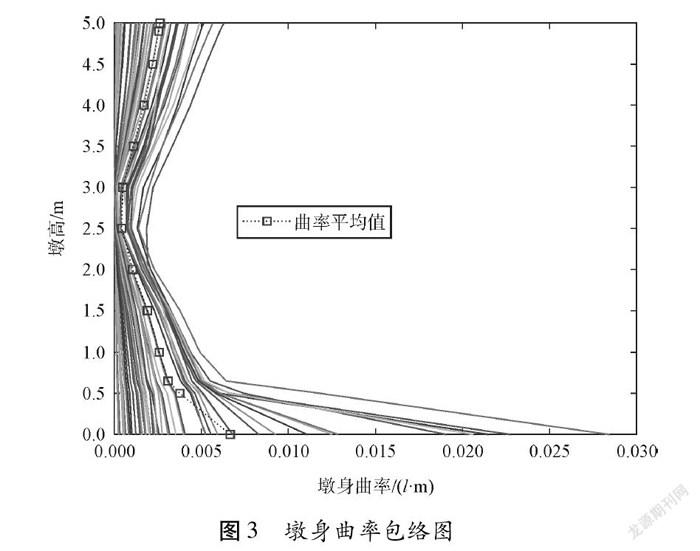
为验证Pushover分析的正确性，采用OpenSees有限元软件对上述结果进行验证。按照地震动的三要素：幅值、频谱特性和持时，在PEER地震中心选取了48条地震波。与Pushover分析方向保持一致，设定地震激励方向为顺桥向，得到每条地震波作用下各个截面曲率最大值，绘制沿墩身方向的曲率包络图，如图3所示。图中实线表示每条地震波的曲率包络图，虚线表示取平均后的包络图。

由曲率包络图可知，在地震动作用下，墩底和墩顶的曲率最大，更容易发生破坏，且墩底的曲率值要大于墩顶的曲率值，即墩底要先于墩顶破坏，这也与Pushover分析的破坏顺序一致。故该T型刚构桥顺桥向的易损位置为墩底截面和墩顶截面。

3 结论

本文采用Pushover静力弹塑性分析方法，对T型刚构桥进行了静力推倒分析，得到如下结论：

（1）Pushover分析计算效率高，实施步骤简单，能够快速确定结构的易损位置T型刚构桥顺桥向的易损位置为墩底和墩顶，且墩底更容易发生破坏;

（2）采用了OpenSees有限元软件，通过计算顺桥向地震动激励下各个截面曲率最大值，根据墩身方向的曲率包络图，验证Pushover分析结果的正确性;

（3）Pushover分析方法仅限于基本振型其主导作用的简单结构，对于受高阶振型影响的复杂结构，还需要进一步地研究。

参考文献

[1] 唐必刚. 基于Pushover和能力谱法的桥梁结构抗震性能研究[D].长沙：湖南大学，2010.

[2] KrawinklerH，Seneviratna G D P K . Pros and cons of a pushover analysis of seismic performance evaluation[J]. Engineering Structures， 1998， 20（4/6）：452-464.

[3] Kilar V， Fajfar P. Peter Fajfar. Simple Pushover Analysis of Buildings Structures. 11th World Co- [J]. Earthquake Engineering & Structural Dynamics， 1997， 26（2）.

[4] 王东升， 翟桐. 利用Push—over方法评价桥梁的抗震安全性[J]. 世界地震工程， 2000， 16（2）：47-47.

[5] 潘龙， 孙利民， 范立础. 基于推倒分析的桥梁地震损伤评估模型与方法[J]. 同济大学学报：自然科学版， 2001， 29（1）：10-14.

[6] 王克海， 季金文， 叶英华. 静力弹塑性分析（Pushover Analysis）在多跨简支梁桥中的应用[J]. 世界地震工程， 2008（1）：132-136.

[7] 张仁龙. 基于推倒分析的桥梁抗震性能评估[D].武汉：华中科技大学，2008.

[8] 李献. 连续刚构桥的静力推覆及其损伤分析[D].长沙：长沙理工大学，2013.

[9] 李贞新. 基于推倒分析法的连续梁桥地震响应简化分析方法研究[D].成都：西南交通大学，2008.

3618501908283