基于改进遗传算法的标签印刷生产调度技术
2021-03-18
(南京理工大学机械工程学院,南京 210094)
0 引言
近年来,全球新技术革命和产业变革正在给制造企业的生产经营活动带来质的变化[1]。企业生产规模扩大的同时,客户需求也越来越复杂,企业为了满足客户的个性化需求,逐步趋向MTO(Make To Order)的生产模式[2]。
标签印刷产品是一种用于简要标明物品的名称、质量、尺寸和用途等的复合材料,它主要以涂硅保护纸作为底纸,在底纸背面涂上离型涂层粘附在涂有粘合剂的防粘纸上,最后经过印刷、模切等工序成为成品标签。标签印刷产品具有种类多、印量小、印品的不可替代性等特点。在日益激烈的市场竞争下,中小型标签印刷企业面临着增强市场竞争力、提高产品加工效率、降低生产成本的迫切需求[3]。但目前我国绝大多数的中小标签印刷企业仍然以传统粗放式生产管理方式为主,企业的信息化水平较低[4],虽然部分企业通过引进企业资源计划(Enterprise Resource Planning,ERP)生产管理系统来提高生产效率,但由于大部分企业所使用的ERP 系统侧重于财务管理[5],缺乏完善的生产调度模块,无法发挥真正有效的作用。
近年来,车间调度问题由于其多约束性、计算复杂和不确定性等特性,一直受到国内外研究学者的广泛关注[6]。国内外学者通过研究和发展,提出了回溯搜索算法[7]、教与学算法[8]、猴群算法[9]和鲸鱼优化算法[10]等算法。刘巍巍等[11]提出用改进变邻域搜索算法求解柔性作业车间调度问题,采用遗传算法进行最优解搜索,并将搜索的结果作为变邻域搜索算法的初始解,提高了初始解的质量。Ye 等[12]以完工时间最小化为目标,提出了平均撤出时间启发式求解零等待车间调度问题(No-Wait Flow shop Scheduling Problem,NWFSP),插入过程采用了目标值增量法来降低算法的计算复杂度。印刷车间调度问题相较普通车间调度问题有所不同,印刷生产的工艺流程较为固定,但部分工艺环节的不确定性与复杂程度较高。针对这些问题,Duan 等[13]提出了一种基于动态增量进化算法的高性能实时数字印刷生产调度算法,相较于规则的启发式算法,该算法具有更高、更稳定的订单准时交货率。赵怡然[14]以作业排序优化为目标研究了印刷行业的生产计划排程,设计了一种循环操作模式的遗传算法,并建立手工排程与自动排程相结合的印刷企业排程系统。
目前国内外的研究主要是基于纸张印刷生产问题,而对于标签印刷生产调度问题的研究相对较少,本文主要针对标签印刷生产调度问题进行研究。上述研究对于求解标签印刷车间调度问题提供了有效的方法,标签印刷过程除具有普通印刷生产加工工艺流程较为固定、部分工艺生产复杂度高等特点外,在实际生产过程中,由于标签印品种类多,根据客户的个性化要求,部分工艺环节存在多台设备可供选择的情况,因此具有柔性作业车间调度的特点。基于以上标签印刷车间调度问题的特点,本文构建了以最小化最大完工时间为优化目标的柔性作业车间调度问题(Flexible Job-shop Scheduling Problem,FJSP)调度模型,并提出了一种改进遗传算法对该模型进行求解,从而对标签印刷车间的调度问题进行研究。
1 标签印刷行业生产管理现状
1.1 标签印刷生产工艺流程
标签印刷产品应用广泛,具有使用方便、撕下即贴、价格便宜等特点。大多数标签印刷产品采用不干胶印刷工艺,图1 展示的是不干胶标签印刷产品的结构图。标签印刷最底层为承印物,在承印物背面涂上离型涂层,粘附在涂有粘合剂的防粘纸上。印刷完成后通过模切工序将防粘纸轧印出所需形状,使用时撕下即贴。
标签印刷工艺流程主要包括印前、印中、印后三个部分。印前包括购买原材料、原稿设计、图像录入、印前图文处理、刀模定制、印刷版制版、油墨调色、机器调机等。其中,油墨调色和调机都非常依赖车间师傅的技术经验,具有很大的不确定性。印中主要包括产品印刷、模切、烫金。印后处理主要包括产品质量检验、分条等。根据客户需求不同,部分标签印刷产品需要进行表面加工,主要包括上光、覆膜、电化铝烫、压痕等操作。
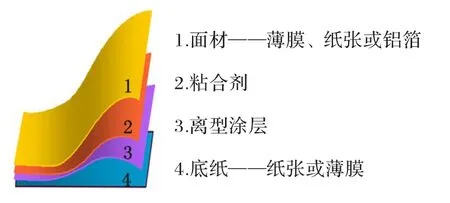
图1 不干胶印刷产品结构Fig.1 Structure of pressure sensitive adhesive printing product
在实际的车间生产过程中,普通不干胶标签的印刷生产工艺流程如图2 所示。上料工序包括开卷、机器调机和油墨调色等工序,但因为这些工序都是人工进行操作,所以在后续的工序研究中直接从印刷工序开始研究。目前不干胶印刷有凸版印刷、胶版印刷、网版印刷、柔印版印刷和凹版印刷这五种印刷方式,其中凸版印刷和胶版印刷方式是目前最为广泛使用的印刷方式。模切又可分为全切、压痕和半切三种模切方式,模切后进入烫金工序,模切与烫金既可以是两台机器,也可以是同一台机器既实现模切工序,又完成烫金工序。品检和分条是标签印刷生产的最后两道工序环节。

图2 不干胶标签印刷工艺流程Fig.2 Procedure of pressure sensitive adhesive label printing
1.2 标签印刷生产过程中存在的问题分析
标签印刷行业在MTO 的生产模式下,其生产过程中存在的特点主要包括:
1)印品种类多、单次印刷量少。标签印刷产品应用领域广泛,且同一产品的标签根据客户企业个性化需求不同,其生产工艺、材料、配色均有所不同,且单次印刷量少,颜色和刀模切换频繁。因此,多品种小批量是标签印刷生产调度的特点,也是难点。
2)客户个性化需求高。客户对标签的大小尺寸、使用材料、颜色配色、图案布局、表面处理工艺以及交货期等需求都因人而异。因此,在满足不同客户需求的前提下,要提高加工效率,对企业车间生产进度的安排提出了很高的要求。
3)不确定性程度高。标签印刷生产的上料准备工序包含了调机、油墨调色工序,而调机和调色时间非常依赖车间师傅经验,不确定性很大。标签印刷产品虽然加工工序严格,但在实际生产中,存在部分工序有多台机器可选择的情况,因此标签印刷生产过程存在较大的柔性。
4)突发状况发生频繁。对于中小企业来说,由于其管理不善,经常会发生紧急订单插入、设备故障、原材料逾期到货等突发事件,传统的人工排产难以保证重调度的高效性与可行性。
在实际生产过程中,对于标签印刷生产过程中存在的多品种、小批量和客户个性化需求高的问题,企业所使用的手工排产方式无法在问题实质上进行有效解决。本文通过结合标签印刷生产过程中存在工序柔性的特点,将柔性作业车间调度模型应用到标签印刷生产调度问题中,构建标签印刷生产调度问题的静态调度模型,并采用改进遗传算法进行求解,从而实现自动排产功能,有效提高加工效率。针对生产过程中突发状况发生频繁这一问题,在实现本文静态车间调度的基础上可以进一步展开动态车间调度,从而有效解决这一问题。针对上述问题的分析,本文对标签印刷生产车间的调度问题开展了相关研究。
2 问题描述
标签印刷企业柔性作业车间调度问题描述为:有n个印品需要在m台加工机器上进行加工,每个印品包含一道及以上的加工工序,工序顺序是提前确定好的,每道工序存在一台及以上的设备可供使用加工,但同一工序所使用的设备不同,加工时间也不同,最终目标是确定每个印品的每道工序在不同机器上的加工顺序,从而使得最大完工时间取得最优值。
下面是针对该车间调度模型的假设:
1)每台机器同一时刻只能加工一个印品。
2)每道工序只能在一台机器上加工。
3)每个印品在加工过程中必须按照既定的工序进行加工,前一道工序加工完以后立即送下一道工序加工。
4)加工过程不允许中断。一件印品一旦开始加工,必须加工到最后一道工序完工,不允许中途停工插入其他工件。
下面对有关符号进行说明:
1)Ji为印品i(i=1,2,…,n);
2)Kq为印品加工工序q(q=1,2,…,p);
3)Mj为机器j(j=1,2,…,m);
4)Di为印品i的交货期;
5)Siq为印品i的第q道工序的开始加工时间;
6)Tiq为印品i的第q道工序的结束加工时间;
7)Ciq为印品i的第q道工序的加工时间;
8)Ciqj为印品i的第q道工序在机器j上的加工时间;
9)Cij为印品i在机器j上的加工时间;
10)Xiqj印品i的第q道工序在机器j上加工其他;
11)Ci为印品Ji的加工完工时间;
12)Cmax为最长完工时间,Cmax=
本文针对标签印刷企业作业车间调度问题采用最长完工时间最短指标为评价指标,相应的数学模型如下。
优化目标:

约束条件:

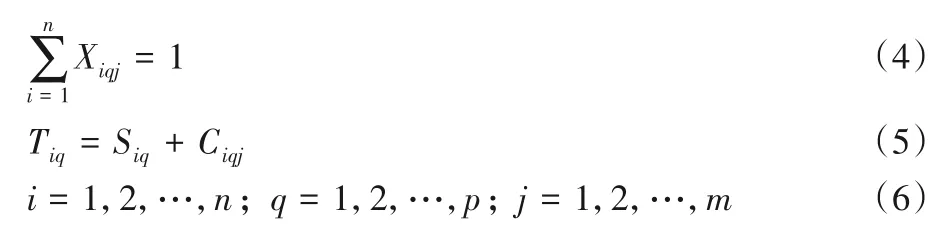
式(1)为优化目标函数,式(2)表示工序约束,式(3)和式(4)表示对加工机器的约束,式(5)表示每一个印品的每道工序开始加工时不能被中断,式(6)表示各下标变量的取值范围。
3 算法操作分析与设计
本文研究标签印刷企业车间调度问题时采用整数编码对简单遗传算法做了改进,根据图3 所示的运算流程,主要步骤为:1)取代传统的二进制编码,根据待优化问题参数集进行整数编码,生成随机初始种群;2)计算染色体适应度值,结合精英解保留策略[15]和轮盘赌法选择适应度值最高的染色体传递给子代染色体;3)进行交叉、变异操作,并采用设计的动态自适应交叉和变异概率,从而得到新的子代染色体;;4)通过迭代次数判断是否结束运行,当满足迭代次数时,将得到的具有最大适应度值的染色体确定为最优解,并通过解码输出最优解。
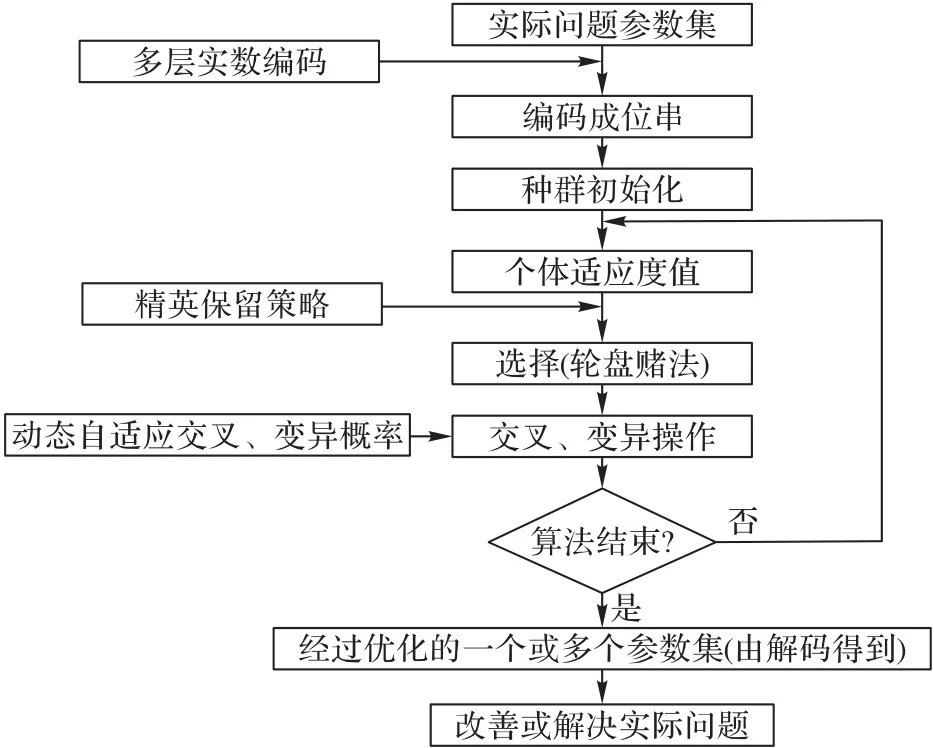
图3 改进遗传算法运算流程Fig.3 Operation flow of the improved genetic algorithm
1)编码。
本文研究的车间调度模型中,待加工印品个数为n,当印品ni的工序个数为mj时,染色体长度为整数串,即每个染色体分为两部分:前半段nimj部分表示所有印品的加工顺序,而后半段nimj部分表示印品加工前半段染色体所对应的工序时的机器号。如图4所示,该染色体包含24个元素,表示有4 个待加工印品,每个印品有3 道工序,共有3 台加工机器去完成所有工序加工。

图4 染色体编号Fig.4 Chromosome codes
图5 为所有待加工印品的加工顺序,其中,该序列中的第一个3 表示待加工印品3 的第一道工序,第二个3 表示待加工印品3 的第二道工序,以此类推所有待加工印品的加工工序顺序。图6所示为加工每道工序时所对应的机器号,其中,M1表示机器1,M2表示机器1,以此类推所有待加工印品加工每道工序时所使用的机器。
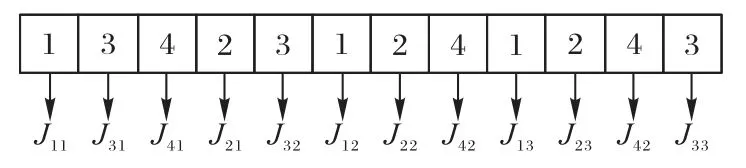
图5 染色体前12位Fig.5 Top 12 chromosomes

图6 染色体后12位Fig.6 Last 12 chromosomes
2)解码。
求得最佳染色体个体后,需要通过解码确定每个印品的每道工序在机器上的加工顺序。本文从染色体的第1 个基因位开始对染色体的所有基因顺序进行解码,假设第I个基因为a,该基因是第X个出现,则该位基因解码表示为a*100 +X,且解码前与解码后的染色体长度保持不变。
3)适应度函数。
在本调度模型中,染色体适应度值函数即为优化指标f,f越大,即工件最长完工时间越短,染色体适应度值越好。适应度计算公式为:

4)选择操作。
选择操作时运用精英解保留策略和轮盘赌法相结合的策略,选择出种群中适应度值最大的染色体直接传递给子代染色体,然后通过轮盘赌法选择其余适应度值较好的染色体传递给子代染色体,染色体选择概率为:
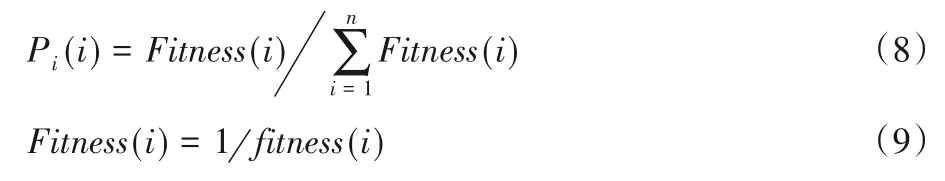
其中:Pi(i)表示在每次的选择中染色体i被选中的概率。
5)交叉操作。
交叉操作分为以下两个步骤:

图7 交叉操作算法Fig.7 Crossover operation algorithm
②交叉后产生新的子代染色体S1'和S2',但S1'和S2'染色体存在某些工件有多余工序和某些工件缺失工序的不可行性问题。比如S1'染色体,在前部分染色体中,工件2出现4 道工序,而工件3 只有2 道工序。S2'染色体的前部分染色体中,工件3 出现4 道工序,而工件2 只有2道工序,因此,对S1'和S2'染色体,分别需要用多余的工序代替缺失的工序,如S1'染色体中用缺失的工件3 的第3 道工序去替换多余的工件2的第4道工序。S2'染色体中用缺失的工件2 的第3 道染色体去替换多余的工件3 的第4 道染色体,并按照交叉前染色体部分显示的每个工件每道工序所使用的机器加工顺序来调整S1'和S2'的至部分的机器加工顺序,调整后的染色体如图8所示。

图8 变异操作算法1Fig.8 Mutation operation algorithm 1
6)变异操作。
通过变异操作可以获得新的子代染色体,从而促使种群进一步进化。本文进行染色体变异操作的步骤:从种群中随机选择父代变异染色体,在前部分染色体中,随机选择两个变异位置Pos1 和Pos2,对调Pos1 和Pos2 位置的元素,并将Pos1 和Pos2 位置上工序所对应染色体后部分中机器加工顺序进行对调,从而得到新的子代染色体。如图9所示,假设随机选择的变异位置Pos1=3,Pos2=3。

图9 变异操作算法2Fig.9 Mutation operation algorithm 2
7)改进的自适应交叉和变异概率。
传统的遗传算法在进行交叉与变异操作时都是选择固定的交叉概率和变异概率,这对求最优解增加了难度。当交叉概率和变异概率取较小数值时会造成搜索范围变小的情况,不利于寻优。而取较大数值时,极易导致在得到最优个体时经过交叉和变异操作后使个体适应度降低。因此,本文在算法操作过程中设计了如式(1)~(3)所示的动态自适应交叉和变异概率,从两个方面改进最优解的寻优过程。一方面,根据个体在种群中的适应度值大小来给予相应的交叉概率和变异概率,规则是适应度值较大的相对给予较大的交叉概率和变异概率,适应度值较小的相对给予较小的交叉概率和变异概率。另一方面,通过采用动态概率遍历种群,使个体在前期以较大的概率进行交叉和变异操作,扩大寻优范围,保证算法不出现早熟现象,而在后期则以较小的概率进行交叉和变异操作,使在前期得到的优良个体不会因为较大的概率而降低适应度值,也进一步加快算法收敛。
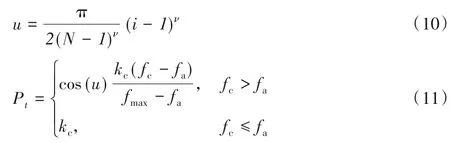
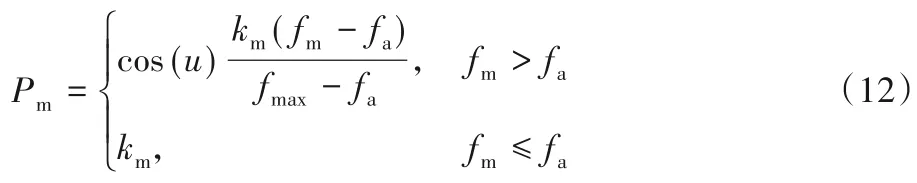
式(10)~(12)中:i为当前迭代次数,迭代到第N次时迭代结束,ν为调整参数,取值范围为区间[1,5]内的整数;Pt为交叉概率;Pm为变异概率;kc和km为常数,取值范围为[0,1];fc和fm分别为两交叉个体较大的适应度值和两变异个体较大的适应度值;fa为种群的平均适应度值;fmax为当前种群最大的适应度值。
4 基准算例仿真及验证
本文以文献[16]的Ft06基准算例来验证改进后的遗传算法的性能。通过Matlab 2019a在Windows 10的64位操作系统上实现。改进遗传算法中的主要参数设置为:种群规模N=100,代沟GGAP=0.9,进化代数G=100,交叉概率Pc和变异概率Pm分别由式(11)和式(12)确定,其中,参数取值为kc=0.9,km=0.12,ν分别取1、2、3、4、5,将改进遗传算法在ν取值分别为1、2、3、4、5 时的运行结果和标准遗传算法(Genetic Algorithm,GA)运行结果进行比较,结果如表1所示。

表1 改进遗传算法与标准遗传算法结果对比Tab.1 Result comparison between the improved genetic algorithm and standard genetic algorithm
由表1 中数据可知,本文算法多次运行的最优解均优于标准遗传算法的最优解,而且当ν=3 时,本文算法的平均迭代次数明显低于标准遗传算法。图10 是当ν=3 时算例进化曲线,通过运算很快得到最佳个体为[3 3 2 6 1 1 3 2 6 4 2 4 5 3 4 6 2 1 1 1 5 4 5 2 3 6 5 2 3 4 5 5 6 1 6 4],图11 是当ν=3 时本文改进算法与标准遗传算法进化对比,由图11 可知,本文算法进化到第12代已经得到最优解,而标准遗传算法迭代到50代才得到最优解。
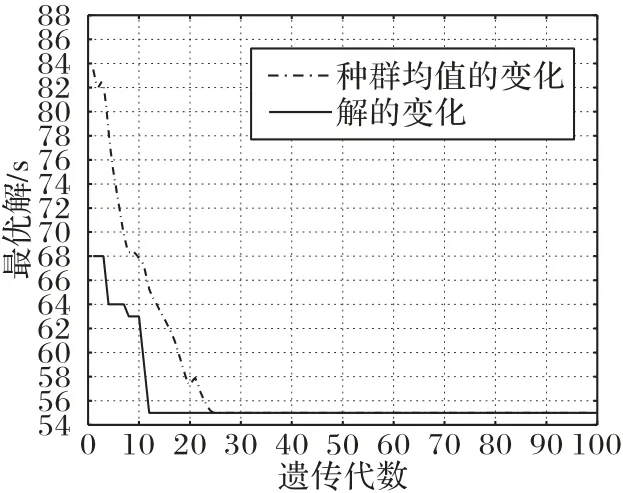
图10 Ft06算例进化曲线Fig.10 Evolution curve of Ft06 example
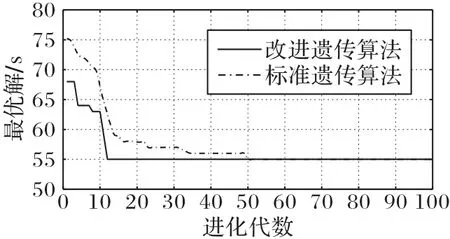
图11 不同算法进化曲线对比Fig.11 Comparison of evolution curves of different algorithm
本文进一步采用文献[17]、文献[18]和文献[19]相同的8× 8、10 × 10 和15× 10 的FJSP 标准算例和文献中的方法来验证算法的稳定性和寻优性能,测试结果如表2所示。由表2可以看出,在3 个标准测试算例中,本文的改进算法均在较短时间内获得了最优解,T表示本文算法求得最优解的时间。

表2 改进遗传算法与其他算法结果对比 单位:sTab.2 Result comparison between the improved genetic algorithm and other algorithms unit:s
根据上述研究可知,本文提出的改进遗传算法不仅具有良好的搜索能力,还有更高的搜索速度,从而验证了本文算法是可行且高效的。
5 标签印刷企业车间静态调度仿真分析
本文以某标签印刷厂的实际生产车间为背景,运用本文所提出的改进遗传算法进行仿真,得出调度方案,并与企业当天实际手工排产方案进行比较分析,从而验证本文改进算法的有效性。运行参数设置为:种群规模N=100,代沟GGAP=0.9,交叉概率Pc=0.8,变异概率Pm=0.6,进化代数G=100。
5.1 标签印刷企业车间实际情况描述
该企业是一家专业生产高档标签印刷制品的印刷企业,具有印刷车间、模切(烫金)车间、品检车间、分条车间。车间主要用于加工不干胶标签,其加工过程主要涉及5 道工序,加工顺序分别为:印刷、模切、烫金、品检、分条。车间有8 台机器,机器1、2 为预涂感光版(Pre-coated photoSensitive plate,PS版)印刷机,机器3 为数字印刷机、机器4、5 为激光数控模切机、机器6 为烫金机、机器7 为品检机、机器8 为分条机。待加工印品的每道工序可选机器如表3 所示,每道工序加工时间如表4所示,时间单位是分钟(min)。
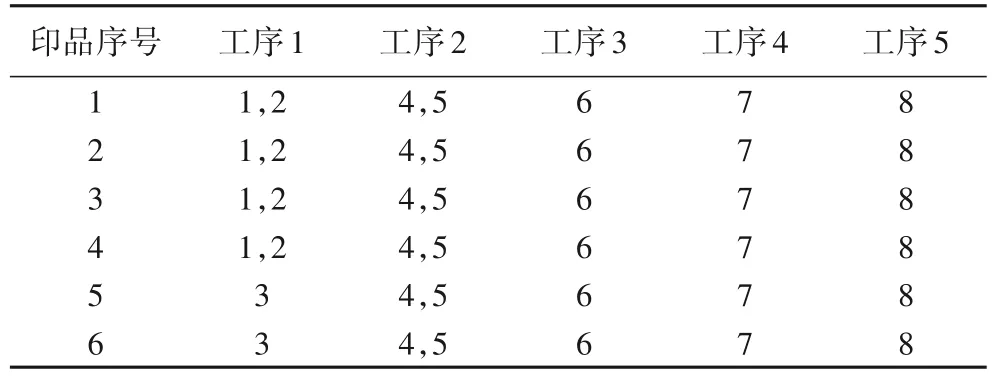
表3 各工序可选机器Tab.3 Selectable machines for different procedures
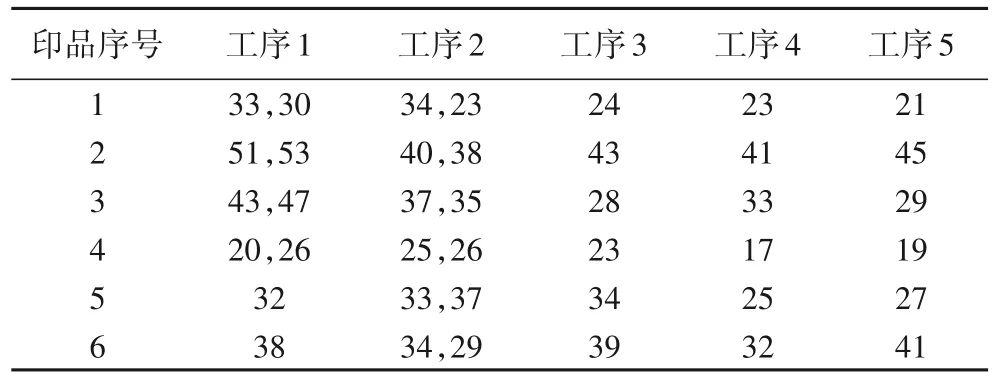
表4 工序加工时间单位:minTab.4 Procedure processing timeunit:min
5.2 仿真结果分析
由如图12 所示的算法搜索过程可知,所有印品迭代到第10次时已经得到最优解。图13所示的加工排产甘特图中,横坐标表示印品加工时间,纵坐标表示工序所使用设备,同一色块表示同一种标签的不同加工工序在不同设备上进行加工,比如,模块201 表示印品2 的第一道加工工序——印刷,且该工序在100 min 时刻在第一台机器上开始加工,至148 min 时刻完成该道工序的加工。由图13 可知,完成6 种标签印刷印品的加工完工时间为322 min,而该标签印刷企业实际当天加工生产该笔订单的时间为648 min,加工效率提高50.3%。由此可见,本文提出的求解标签印刷生产调度模型的改进遗传算法可以有效提高加工效率,大大提高机器使用率,缩短了印品生产加工周期,可以直接用于标签印刷企业的实际生产调度。

图12 改进遗传算法搜索过程Fig.12 Search process of the improved genetic algorithm
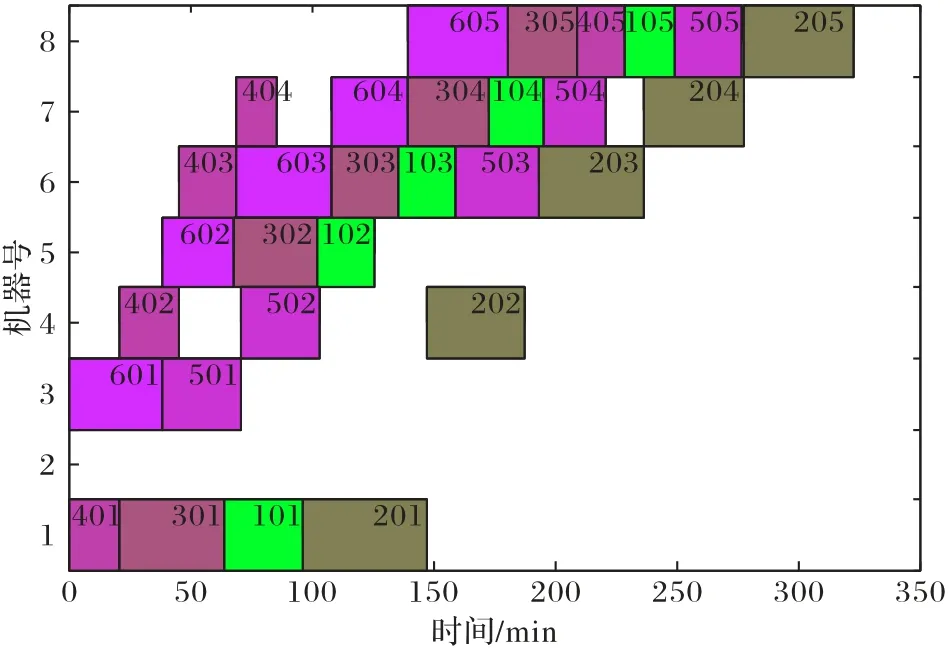
图13 加工排产甘特图Fig.13 Gantt diagram of production scheduling
6 结语
本文基于标签印刷生产过程中存在印品种类多、单次印刷量少、客户个性化需求高等问题,并针对其车间调度问题复杂程度高、具有不确定性等特点,构建了以最小化最大完工时间为优化目标的FJSP 调度模型,并提出了一种改进遗传算法对该模型进行求解。算法首先从编码方式和个体选择两方面进行改进,整数编码方式具有稳定性好、收敛快等特点,在选择阶段采用轮盘赌法并引入精英解保留策略来确保算法的收敛性。还提出了一种动态自适应交叉和变异概率,在前期实现较大范围寻优,避免算法发生早熟现象,后期保证得到的最优个体不遭到破坏,实现较快收敛。实验过程采用标准算例对算法的有效性和稳定性进行了验证,并针对某标签印刷企业的实际生产情况,利用本文的改进遗传算法求解出该标签印刷车间的生产调度方案,与实际手工排产完工时间进行比较分析得出,在该模型下加工效率提高了50.3%,使得机器使用率大大提高,缩短了印品生产加工周期,有效解决了交货期不准时的问题,进一步表明了本文算法求解标签印刷产品生产调度问题的可行性和有效性。
但本文研究只针对标签印刷生产加工的静态车间调度模型,在实际生产过程中,经常会发生紧急订单插入、设备故障、原材料逾期到货等突发事件,因此,在后续的研究中会继续对动态车间调度问题进行深入研究。
