基于k-means++的动态构建空间主题R树方法
2021-03-18
(江苏大学计算机科学与通信工程学院,江苏镇江 212013)
0 引言
随着移动互联网的迅猛发展,推动了基于地理位置信息服务(Location-Based Service,LBS)的大量普及。最典型的例子就是地图类的服务,比如百度地图、高德地图、外卖平台等,伴随着的还有空间数据的极速增长。由于空间数据的多维性以及位置关系的多样性,空间数据的处理与存储问题已经成为了亟待解决的问题。大多数空间数据索引的构建是通过R-树来完成的,R-树是B-树在高维上的扩展[1],R-树结构简明、动态性高、适用范围广[2]。在进行R-树树空间区域检索时,从根节点出发,由顶向下逐层缩小范围直到叶子节点满足搜索条件。
目前,学术界对R-树的研究主要有两个方面:一种是针对空间聚类算法方面的研究;另一种是针对R-树结构相关算法调整方面的研究。聚类算法构建R-树中,将R-树操作中的分裂算法改进为聚类算法中的多路分裂,对R-树的研究转向为聚类构建。2016 年胡昱璞[2]提出动态确定k值的空间聚类算法(Dynamical K-Value spatial Clustering algorithm,DKSC),该算法通过聚类划分空间数据,把同一子空间的数据组织在同一个子树下,从根节点到叶子节点逐层构建R-树,形成高效的R-树空间索引。2017 年彭召军等[3]针对传统的k-means聚类算法对初始值非常敏感,聚类过程较为复杂的问题,在R*-树的构建过程中引入聚类技术,对R*-树的基本结构加以改进,提高索引树的空间利用率。R-树相关算法的调整研究,一般是对R-树插入算法中的分裂算法重构或是改变插入节点模式。2017 年杨泽雪[4]针对已有的QR-树(Quad R-tree,QR-tree)索引结构在节点分配中,可能存在较小的对象落入较大的节点中的问题,提出一种混合空间索引结构松散QR-树(Loose Quad R-tree,LQR-tree),有效地解决了节点下移的问题,弥补了QR-树的查询缺陷。
现有的聚类构建R-树方法存在着各种优缺点。例如利用k-medoids 算法[5-6]聚类空间数据,构造索引的过程中,需要指定聚类数k值,这不符合空间数据的分布不规律性,k值不定;又如利用聚类算法构建空间数据索引时,初始聚类中心随机或指定选取,聚类结果容易受到离群空间数据的干扰;现有的聚类构建R-树方法中,改进了各类聚类算法,但仅仅是基于空间数据地理位置上的改进,并没有考虑空间数据文本间的联系,在聚类中心的选取上未考虑语义级的选取,只是基于欧氏距离的选取。
k-means++[7-8]聚类算法对k-means 算法确定初始聚类中心提出改进,步骤如下:1)从数据集中随机选择一个样本作为初始聚类中心;2)计算每个样本到聚类中心的距离;3)选取距离前一个聚类中心距离最远的样本作为新的聚类中心;4)重复步骤2)、3)得到k个聚类中心。本文就是对聚类中心选取以及k值确定作出优化。
主题模型主要利用吉布斯采样、变分推断、非负矩阵分解等机器学习算法从高维稀疏的文本特征空间中推断出潜在主题信息[9]。以潜在狄利克雷分布(Latent Dirichlet Allocation,LDA)模型[10]为代表的主题模型是一种非监督的机器学习方法,它能有效地提取大规模文档集和语料库中的隐含主题,其良好的降维能力、建模能力及扩展性,使其成为近年来主题挖掘领域中热门研究方向之一[11]。空间数据包含空间位置数据和空间文本数据[12-14],现有的构建R-树仅仅是对空间位置数据进行划分;而空间文本数据,例如:肯德基、沙县小吃,是具有关联性的文本数据,可划分为美食,是对文本数据的分类。因此,将主题模型LDA 引入进R-树的构建中理论上具有可行性[15]。
现有的R-树空间聚类技术在聚类中心的选取上通常通过随机指定或者只计算空间数据间的欧氏距离,未考虑空间数据中文本数据间的主题相关度。本文在k-means++的基础上,提出了一种动态k值构建空间主题R-树(Topic R-Tree,TR-tree)方法,通过引入LDA 主题模型,优化聚类中心选取、优化聚类测度函数来动态确定k值,使得聚类算法构建R-树结构更加紧凑,R-树节点间文本数据关联性更高,从而提高R-树检索效率。
1 相关定义
针对k-means++的动态构建空间主题R-树方法中存在的问题,进行如下定义:
定义1聚类均值点:
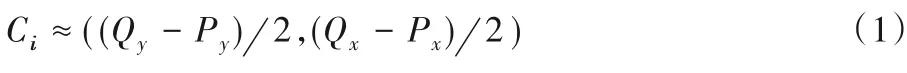
数据均值点Ci(i=1,2,…,k)为划分区域的距离中心最近的空间数据,其中Q、P分别为可以划分一个区域的两个空间数据。
定义2距离指标:

其中:n表示一个区域下空间数据的数量;D表示区域面积(m2);若一个区域下的空间数据到数据均值点Ci的距离小于R,则将该数据记为Ci的邻近空间数据。
定义3聚类测度函数:
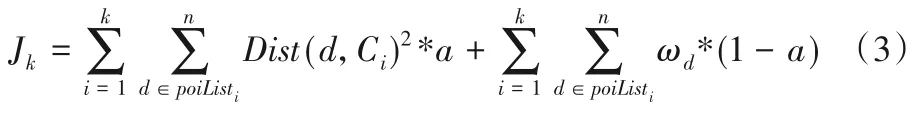
聚类测度函数的作用是在聚类划分的过程中,直到聚类测度函数值收敛,此时确定聚类数k值。本文设计的聚类测度函数将距离及主题概率结合,得到poiListi中与每个数据均值点Ci的距离,以及它们的主题概率之和。其中,poiListi为邻近空间数据集,d指poiListi中的单个空间数据,k为聚类数,Ci为数据均值点,a为关于距离及主题的平衡参数,取值在0~1。a越大代表倾向距离影响因素,越小代表倾向主题概率影响因素,ωd为每个空间数据与数据均值点相同的主题的概率。在每次划分一个区域后通过距离指标R得到其邻近空间数据后,计算此时对应k值的聚类测度函数Jk,并与上一个k值所对应的Jk-1比较;若此时函数收敛则取当前k值为当前区域聚类数,若函数分散则继续划分,从而动态确定k值。
2 构建TR-tree
k-means++算法优化了k-means算法的聚类中心选取的问题,但同样在k值选取上采用先确定k值。在不确定的空间数据中,先确定k值不符合实际空间数据的分布,因此本文改进了k-means++算法,采取动态确定k值的算法,更符合空间数据分布不确定的情况,使得聚类算法构建R-树结构更紧凑,R-树空间索引效率更高。
算法的基本思想是:获取指定的最小外接矩形,将其看作一个大类,初始聚类数k=1,根据定义1 得到最小外接矩形(Minimum area Bounding Rectangle,MBR)[16]初始类数据均值点;通过定义2距离指标R得到当前数据均值点Ci邻近空间数据集poiListi;通过文本主题分类对poiListi中的poi数据进行分类,得到每个空间数据的主题分布概率ωd;计算当前k值对应的聚类测度函数值Jk;将Jk与前一次聚类测度函数值Jk-1进行比较,若此时函数收敛,则取当前k值为当前R-树这一层的聚类数;若此时函数发散,则通过距离选取距离前一个数据均值点最远的空间数据作为后续数据均值点,得到后续MBR;对新的MBR继续划分,直至k值递增至M;其中M为R-树节点的最大条目数,对于R-树中的节点,M和m分别为一个节点中的最大和最小条目数,如果节点是根节点,则该节点所容纳的条目数范围为2~M;如果节点不是根节点,则该节点所容纳的条目数范围为m~M。通过主题概率,找出poiListi中出现次数最多的地理数据作为聚类中心,再递归找出各个MBR 的聚类中心PK;以k个聚类中心PK作为根节点的子节点,进行聚类构建R-树,构建R-树时,优先选取与PK主题概率相似度较高的空间数据并且该空间数据满足距离指标R,保证每个节点上的子树主题概率相似度较高,PK为poiListi中出现概率最高的空间数据,在进行R-树构建时,又优先选择与PK主题概率相似的空间数据,因此提高了子树的主题关联度;假设父节点有n个空间数据,检查每个聚类后的空间数据个数N,子节点的聚类个数为k,若N=n/k,则此时停止分配;若N>n/k则通过距离分配到最近的且未填满的PK;以每个子节点作为子树的根节点重复进行聚类构建R-树,形成主题R-树。
构建TR-tree主要分为3个步骤:
步骤1 得到k个聚类数,例如图1 所示,C1和C16可划分一个MBR,C8为该区域初始聚类均值点,选取距离C8最远的C16划分新的区域R2;计算此时的J2,函数分散继续划分,选取距离C16最远的C1及距离C1最远的C11为新的区域R1,再次判断J3;从而得到聚类数k值。

图1 确定k个聚类簇Fig.1 Determination of k clusters
步骤2 聚类中心的确定:通过步骤1得到每个数据均值点Ci的邻近空间数据集poiListi,将出现概率最多的数据作为此区域的聚类中心。
步骤3 构建空间主题R-树:构建时优先选择邻近空间数据集poiListi中与聚类中心PK主题相似度较高的空间数据,例如图2 所示,根据一个空间区域初始数据均值点为C6,通过距离指标R得到poiListi={C5,C6,C7,C8,C9},计算主题概率,计算聚类测度函数值并且重新划分;得到R3、R4、R5、R6空间区域并且对其中主题概率较大的空间数据作为聚类中心;在构建R-树时,C5满足R3、R5 的距离指标R,但其主题概率偏向C2,因此划分到R3中,构建的R-树如图3所示。
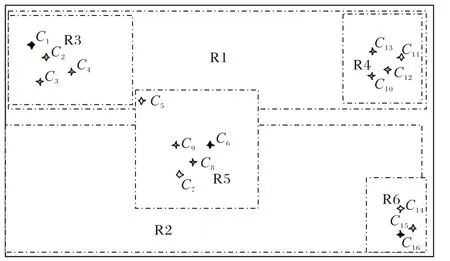
图2 根据距离指标划分MBRFig.2 MBR division by distance index
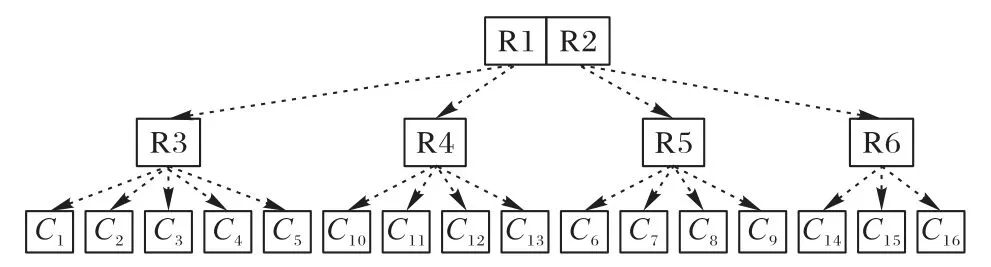
图3 TR-treeFig.3 TR-tree
构建TR-tree算法伪代码如下。
输入:n个空间数据D={d1,d2,…,dn}
输出:子树头节点


3 实验与结果分析
3.1 实验环境与数据集
为了验证TR-tree 的性能,将本文提出的TR-tree 与R*-树[3]、NDRKR-树(Nearest neighbor Dynamic K R-tree,NDRKRtree)[17]进行对比,R*-tree 采取改进的k-means 算法进行聚类构建,NDRKR-tree 采取改进的k-means 算法以及通过欧氏距离确定聚类测度函数,本文优化聚类测度函数,引入LDA 主题模型,进行以下对比实验。实验平台为2.3 GHz Inter Corei5 戴尔笔记本,操作系统为Window 10,编程语言是Python,编程工具为PyCharm。数据集分为两个部分:空间文本数据为阿里云天池公开的天猫商品描述文案数据(实际数据进行LDA 主题映射时,每一段语句都会分为很多类主题,选取主题概率最高的推断其为这类主题,对大量数据进行LDA主题映射有较好的主题分类);空间位置数据为公开的杭州市POI地理位置数据。
为了使实验结果具有代表性,实验数据中空间文本数据随机取天猫商品描述文案D1:15 000、D2:20 000、D3:25 000、D4:30 000 个,地理位置数据随机取杭州市公开的POI 数据D1:15 000、D2:20 000、D3:25 000、D4:30 000 个,将其整合为空间数据。实验参数:M为R-树节点的最大数目其与动态k值相关,平衡参数a代表主题与欧氏距离的关系。
3.2 性能及实验分析
取参数M=10,平衡参数a=0.2,TR-tree 与R*-tree、NDRKR-tree 进行构建时间、查找时间以及节点间重叠度进行对比实验。
3.2.1 构建R-tree时间
由图4 知,TR-tree 在整体的构建时间上相较于其他两个构建算法上时间略有增加,这主要是由于本文提出的算法在确定聚类中心时增加了LDA 主题映射从而增加了算法的时间复杂度。

图4 不同算法构建R-tree时间的对比Fig.4 Comparison of R-tree construction time of different algorithms
3.2.2 算法查找时间
从图5知TR-tree的查找效率相较于其他两个算法有明显的提升,尤其在数据量大的情况下较为明显,这是由于随着数据的增加,数据间的主题相关度更加明确,数据间的关联度也更高,从而提升了查找效率。
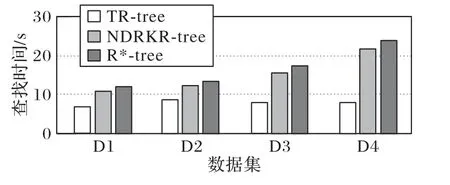
图5 不同算法查找时间的对比Fig.5 Comparison of search time of different algorithms
3.2.3 节点间重叠度
图6 为3 个算法在节点重叠度方面的比较,从结果可知TR-tree 在数据量越大时,节点间重叠度相较其他两个算法越小,正是由于数据间的主题相关度越高,子树节点间的主题更加明确,从而使节点的重叠度降低,从而查询效率越高。
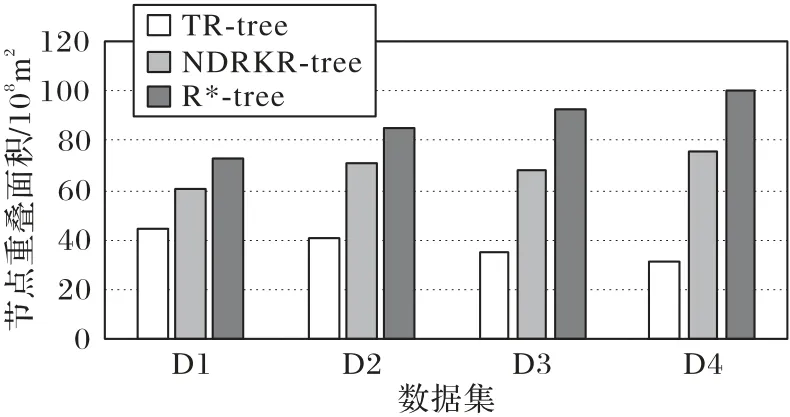
图6 不同算法节点间重叠度的对比Fig.6 Comparison of overlapping degree between nodes in different algorithms
3.2.4 多组平衡参数
表1表示取参数M=10,平衡参数分别为0.2、0.5、0.8下,数据集D1、D2、D3、D4 在TR-tree 算法中节点间的重叠度。由式(3)可知,a越小代表聚类测度函数与主题关联度越高,从结果可知随着数据的增大,a越小节点间的重叠度越小,间接说明主题关联度越高,TR-tree节点重叠度越低。

表1 不同平衡参数的节点重叠度Tab.1 Degree of overlapping degree between nodes with different balance parameters
表2 为TR-tree 在数据集D1、D2、D3、D4 时查找时间的实验数据。由表2 可知,当节点数目取20,a取0.2,数据量增大时,查找效率优于其他对比数据,表明当数据量增大时,主题映射较为准确,对聚类测度函数起到了约束作用,从而影响k值的确定以及节点间的关联度,进而提高了查找效率。
综上所述,本文提出的基于k-means++的空间主题R-树,在查找效率、节点间的重叠度在空间数据量较大时,优于其他两个对比算法。

表2 数据集查找时间 单位:sTab.2 Dataset search time unit:s
4 结语
在k-means++算法的基础上,本文结合LDA 主题模型,优化动态选取聚类中心算法,提高R-树子树的主题关联度;优化聚类测度函数,通过距离加主题概率确定聚类数k值,动态构建空间主题R-树。通过实验将本文方法TR-tree与R*-tree、NDRKR-tree 进行对比,验证了TR-tree 在空间查找效率以及节点重叠度方面具有明显的优势。接下来可对TR-tree 进行下一步的研究,主要在如何提高R-树的构建速度方面,在聚类测度函数中,需要计算空间数据间的距离,时间复杂度有待提升,以及如何对聚类测度函数进行进一步的优化。
