PID控制策略在大阵面天线横展控制系统中的应用仿真
2021-03-18陈曦,汤辉
陈 曦,汤 辉
(中国电子科技集团公司第三十八研究所,合肥 230088)
0 引 言
为适应现代战争的需要,一方面,雷达及电子对抗等装备的天线尺寸越来越大;另一方面,需要该类装备的大尺寸平面阵列天线在满足公路、铁路机动运输的前提下,进入阵地后能够快速架设和撤收,实现战斗和撤离形态的快速转换。在上述需求牵引下,世界领先的天线体积压缩技术应运而生。这种天线的特点是可压缩天线结构部分由多个生根于展开机构的独立列骨架或行骨架组成,这些骨架单元相互之间是柔性连接的,组成风琴式或风帆式结构。天线的刚度和精度由两个或多个液压驱动的展开机构保证。展开机构必须全行程严格同步,否则易造成天线骨架变形甚至撕裂。因此,在-40°~55°范围内,双(多)油缸同步技术成为技术实现和安全性的关键。
某型号天线阵面的双油缸同步横展和收缩状态示意图如图1所示。该大阵面天线结构以电液比例阀+液压油缸作为驱动机构带动天线骨架橫向展开与收缩,控制系统的核心任务是保证同一驱动对象的驱动机构之间的运动同步性。已知该型号的雷达天线阵面橫展时所使用的液压传动系统参数如下[3]:
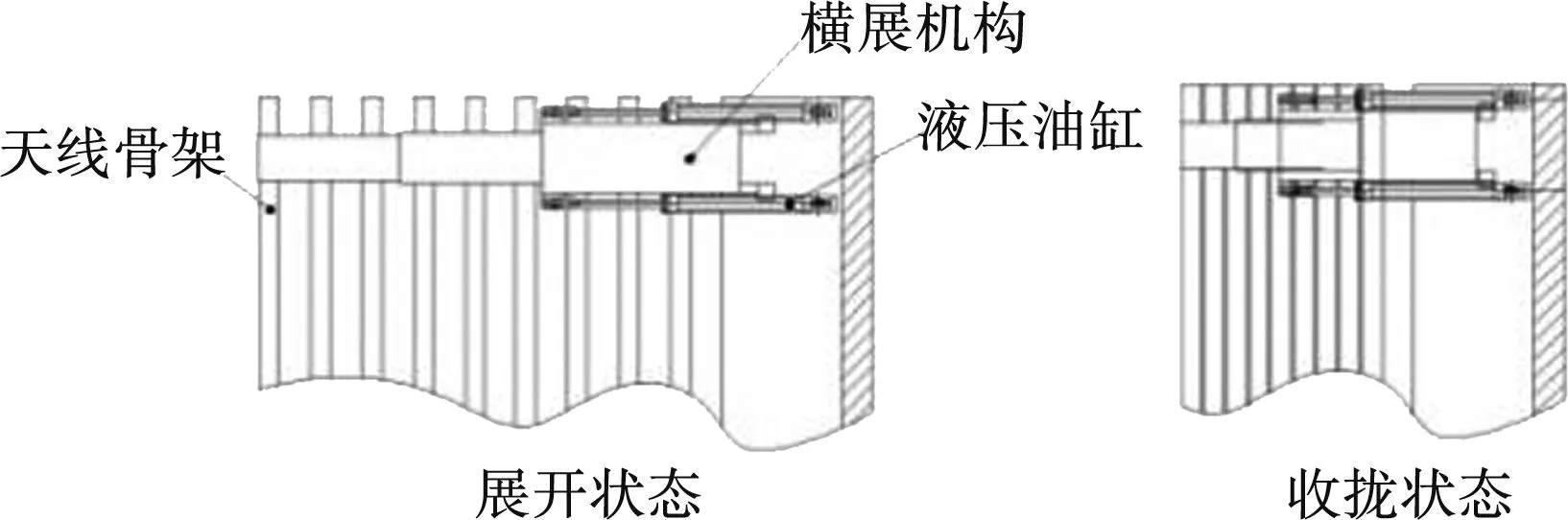
图1 部分天线阵面的伸展与收缩状态
液压缸无杆腔直径:D=63 mm;
液压缸有杆腔直径:d=40 mm;
液压源压力:Ps=1.6×107Pa;
液压油密度:ρ=0.87×103kg/m3;
液压缸的行程:L=705 mm;
工作压力:pL=1.0×106Pa。
根据推导[4]可得到单套比例阀控非对称液压缸系统的传递函数为
(1)
1 基于多段速同步调整算法的大阵面天线横展与收缩
图1所示的多油缸同步系统本质上依然是建立在双缸同步关系下的“一主多从”型同步,通过对双缸同步模型进行仿真,便可清晰地观察不同算法在多油缸同步控制中的表现。一个典型的双缸闭环同步控制系统框图如图2所示。
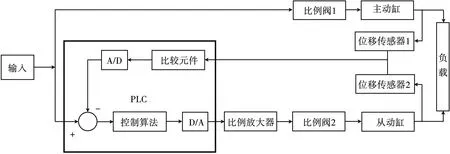
图2 双油缸闭环同步控制系统框图
系统的核心控制器是可编程控制器(PLC),位移传感器实时向PLC上传两个油缸各自的活塞杆相对于初始状态的位移量,PLC内的控制算法通过计算两缸的位移差值得到同步误差E,而后控制算法根据E值调整输出到比例放大器的信号,从而调整从动缸的运动速度,使两个液压油缸保持同步[1]。
目前工程上最常见的多驱动机构同步控制策略是多段速同步控制方法,即根据天线阵面的实际精度要求和具体结构形式设定两个油缸之间允许出现的最大位移同步误差值Emax,将同步误差E可能出现的取值范围[-Emax,Emax]分成n段,每一段设定一个固定的速度值,实现不同位移误差下的阶梯式调速。工作状态下PLC实时获取并比对位移传感器检测的位移量,判断出当前从动缸需要以何种速度与主动缸保持同步。速度的设定则是由PLC输出模拟量信号到比例放大器进而控制电液比例阀,达到调节液压油缸运动速度快慢的目的。
下面通过Simulink对这种算法进行仿真,系统仿真框图如图3所示。系统主要包含4个部分:两个油缸的独立信号源,用于表示上位机对油缸运行速度的控制;主动缸运动控制子系统;从动缸运动控制子系统,相比于主动缸子系统部分增加了多段速同步调整算法控制环节;位移误差计算环节,首先将主从双缸输出的速度信息进行积分获得实时位移,对两缸的位移差值分别叠加一个幅值在±1之间的均匀分布随机数模拟随机干扰之后,将两缸位移值作差得到位移差值,并将位移差值作为控制反馈输入至从动缸,进而调节从动缸速度,达到双缸同步的目的。

图3 Simulink中搭建的基于多段速同步控制方法的双缸位移同步控制系统仿真
设定仿真时间为10 s,最大同步误差Emax为20 mm,分别调整两个油缸子系统的控制信号输入来模拟不同的场景。当主动缸与从动缸的位移差为正时,从动缸需要提速追赶主动缸,例如当同步误差E∈[15,20)时,设置从动缸速度增至20 mm/s;当主动缸与从动缸的位移差为负时,从动缸需要减速等待主动缸,例如当同步误差E∈(-15,-10]时,设置从动缸速度降至5 mm/s。考虑到天线阵面在实际展开过程中不可避免地受到来自环境因素和自身结构变化导致的震荡的影响,仿真时对主从两缸每次采样时的位移值附加一个幅度在[-1,1]之间的均匀分布随机数,以此模拟真实的工程环境。
模拟情景1:某一油缸不动作
在实际工程中最常见的双缸同步故障原因有油路故障、电磁阀故障或结构件卡死等,导致其中一个油缸停滞不动。在MATLAB中设置主动缸速度为0 mm/s,从动缸正常启动,以多段速同步调整算法模拟控制从动缸的速度,仿真结果如图4、图5所示。
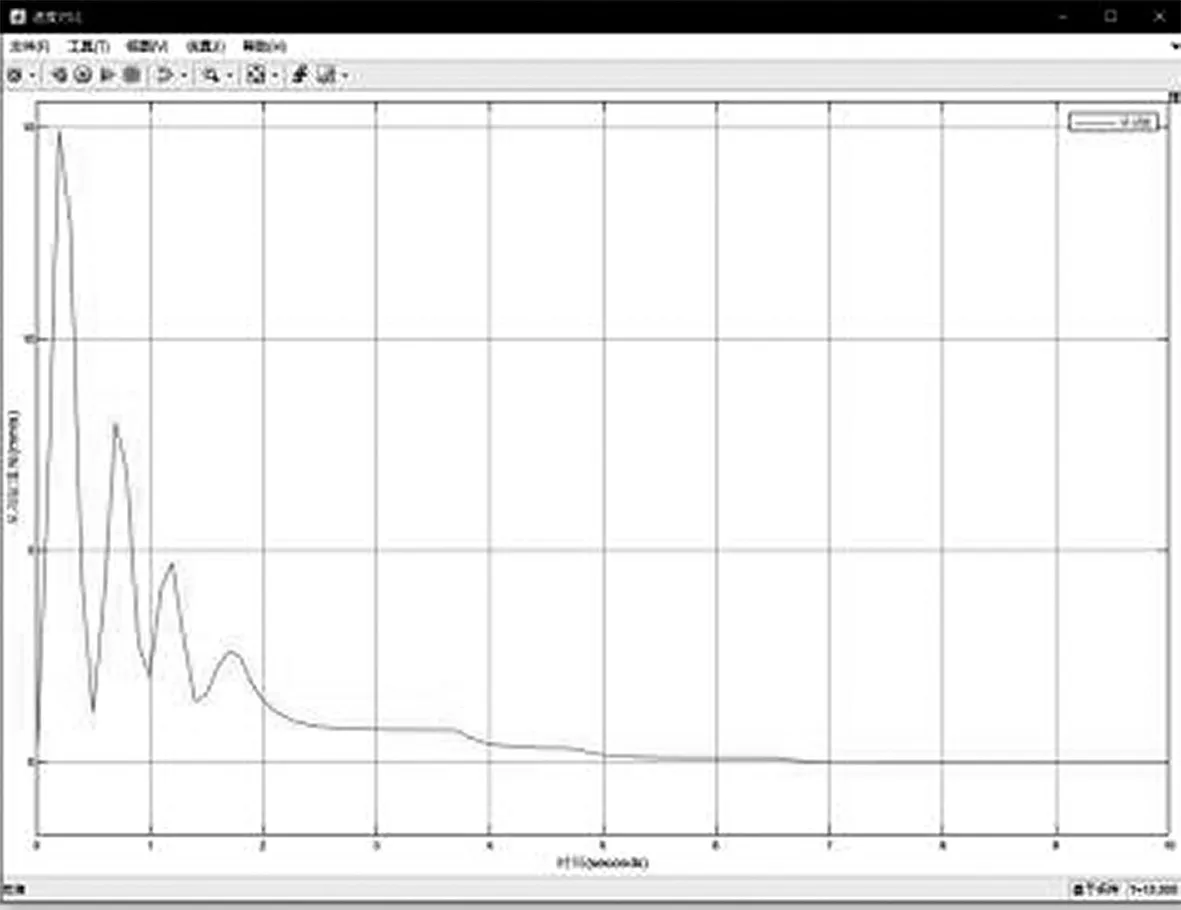
图4 从动缸运动速度随时间变化曲线
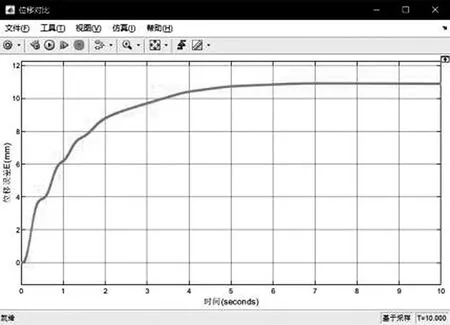
图5 两缸位移同步误差变化曲线
模拟情景2:从动缸在运行3 s后卡顿1 s
与上个模拟场景类似,在双缸同步过程中油路故障或者负载变化等原因可能导致某一油缸与另一油缸之间的位移差值瞬间变大。在MATLAB中将从动缸运行过程中的某一秒的速度置为零,模拟卡顿现象。仿真结果如图6、图7所示。
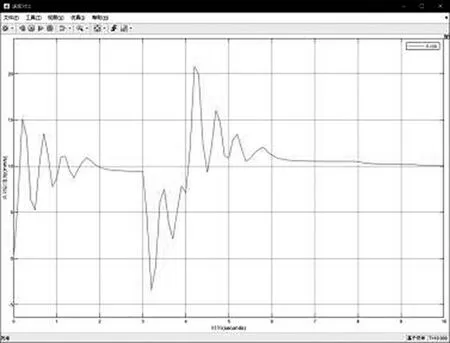
图6 从动缸运动速度随时间变化曲线
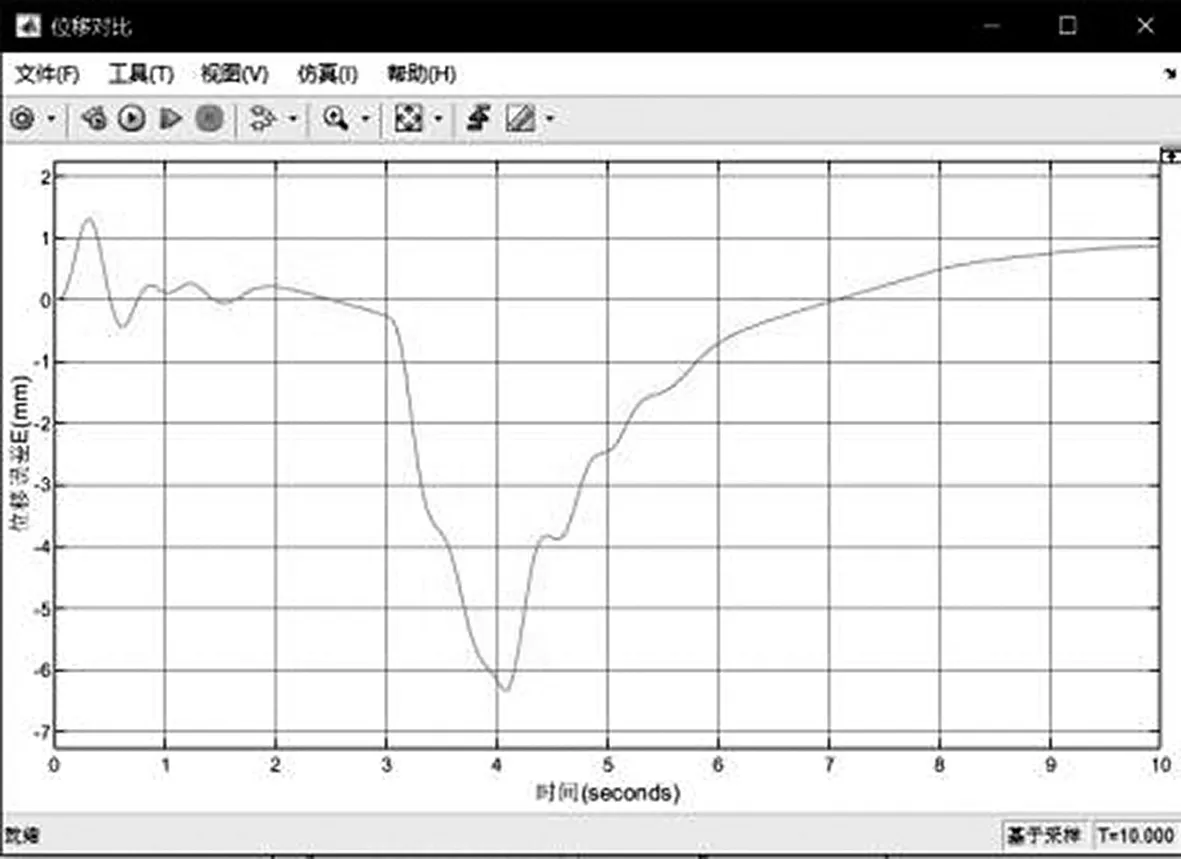
图7 两缸位移同步误差变化曲线
由上述不同场景的仿真结果可知,多段速同步调整算法能够适应精度要求不高的同步控制场景,算法结构简单,易于实现和调试,通用性强,但也可以看出该算法对突发情况的综合响应时间较长,最终达到稳态时难以消除静态误差,控制过程中振荡较大,抗干扰能力不强。
2 基于PID算法的双缸同步控制策略
在图1所示的天线阵面横展机构的实际工程应用中,为了获得对突发情况更快的响应速度、更好的抗干扰性以及更高的控制精度,选择以PID控制策略代替多段速同步调整算法。PID控制是工程领域一种较为成熟的算法。PID控制子程序通过对从动缸与主动缸之间的位移误差E(t)进行比例(P)、积分(I)和微分(D)的线性组合以构成控制量,对从动缸的速度进行校正和控制[2]。PID控制方程为
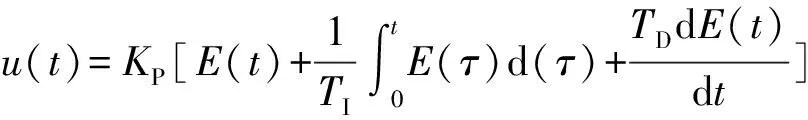
(2)
式中,KP为比例系数,用于加快系统的响应速度,提高系统的调节精度,成比例地控制信号的偏差信号,偏差一旦产生,控制器立即产生控制作用,快速减少偏差;TI为积分系数,主要用于消除系统的静态误差,提高系统的无差度,积分作用的强弱取决于积分时间常数,TI越大,积分作用越弱,反之越强,但若TI过小,在响应过程初期会产生积分饱和现象,从而引起响应过程的较大超调;TD为微分系数,主要用于改善系统动态特性,可以反映偏差信号的变化趋势,并能够在偏差值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间,但TD过大会降低系统的抗干扰性能。
利用前面计算出的系统传递函数,可在Simulink环境中轻松实现双缸同步的PID控制仿真。
在Simulink中设置仿真时间为10 s,双缸速度初始值为0,正常运行时速度均为10 m/s,选择“主从控制”策略搭建大阵面天线横展过程的仿真。如图8所示,主从两套阀控缸子系统分别形成闭环位置控制,以双缸位移差值作为反馈,使用PID算法调节从动缸的速度,最终实现双缸同步误差保持在零位附近。与上述仿真多段速同步调整算法时相同,在两缸位移量上分别叠加一个独立的、大小在±1之间的均匀分布随机数,用于模拟系统实际运行时可能出现的环境扰动。通过Simulink自带的PID参数调节器设定参数P=0.27,I=0.09,D=0.09,滤波器N=8.85。
如图8所示,在Simulink中搭建的基于PID控制的主从方式双缸位移同步控制系统与图3所示的系统基本相同,仅在从动缸控制子系统中将多段速同步调整算法模块替换为了PID控制模块[6]。
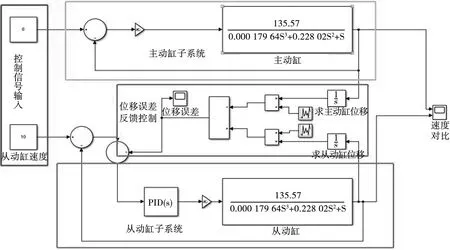
图8 Simulink中搭建的基于PID算法的双缸位移同步控制系统仿真
模拟场景1:主动缸因某种原因不动作
与分段控制仿真时相同,为了模拟实际工程中其中一个油缸停滞不动的情况,在MATLAB中设置主动缸速度为0 mm/s,从动缸正常启动,以PID算法模拟控制从动缸的速度,仿真结果如图9、图10所示。
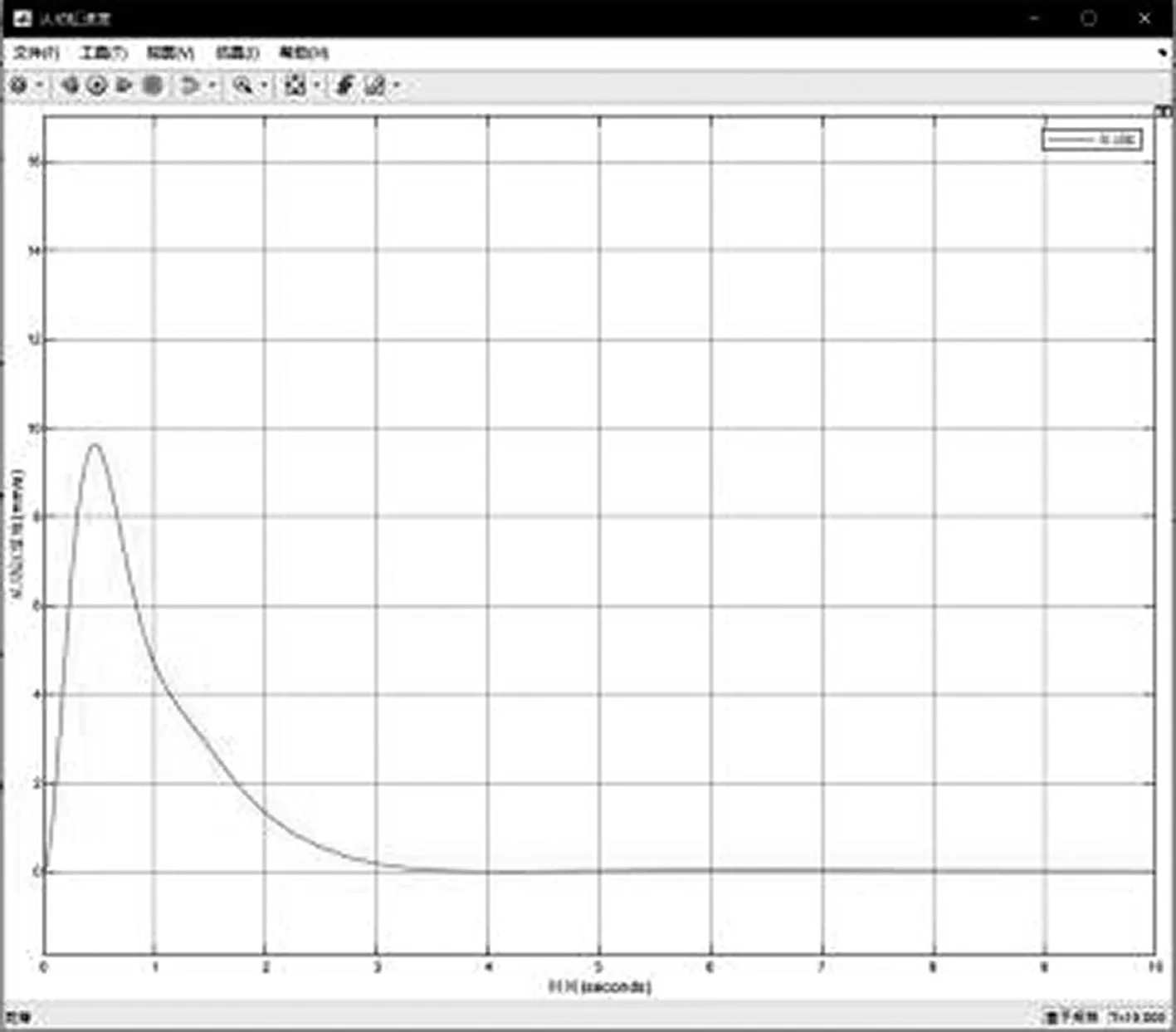
图9 模拟场景一从动缸速度变化曲线
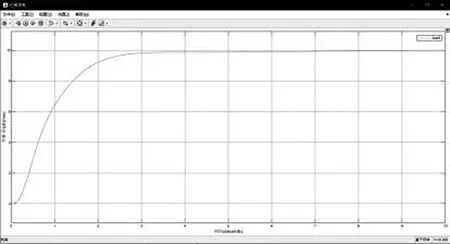
图10 模拟场景一双缸位移差曲线
与多段速同步调整算法相比,PID控制算法用时4 s便将速度降为零,累积同步位移误差更小,且调速曲线平滑,受随机误差干扰影响较小,加减速均响应迅速,在实际工程应用中这样快速、稳定的响应能够极大程度地避免故障对天线阵面的损坏。
模拟场景2:从动缸在运行3 s后卡顿1 s
与分段控制仿真时相同,为模拟双缸同步过程中由于油路故障或者负载变化等原因可能导致某一油缸与另一油缸之间的位移差值瞬间变大的情况,在MATLAB中将从动缸运行过程中的某一秒的速度置为零,模拟卡顿现象。仿真结果如图11、图12所示。
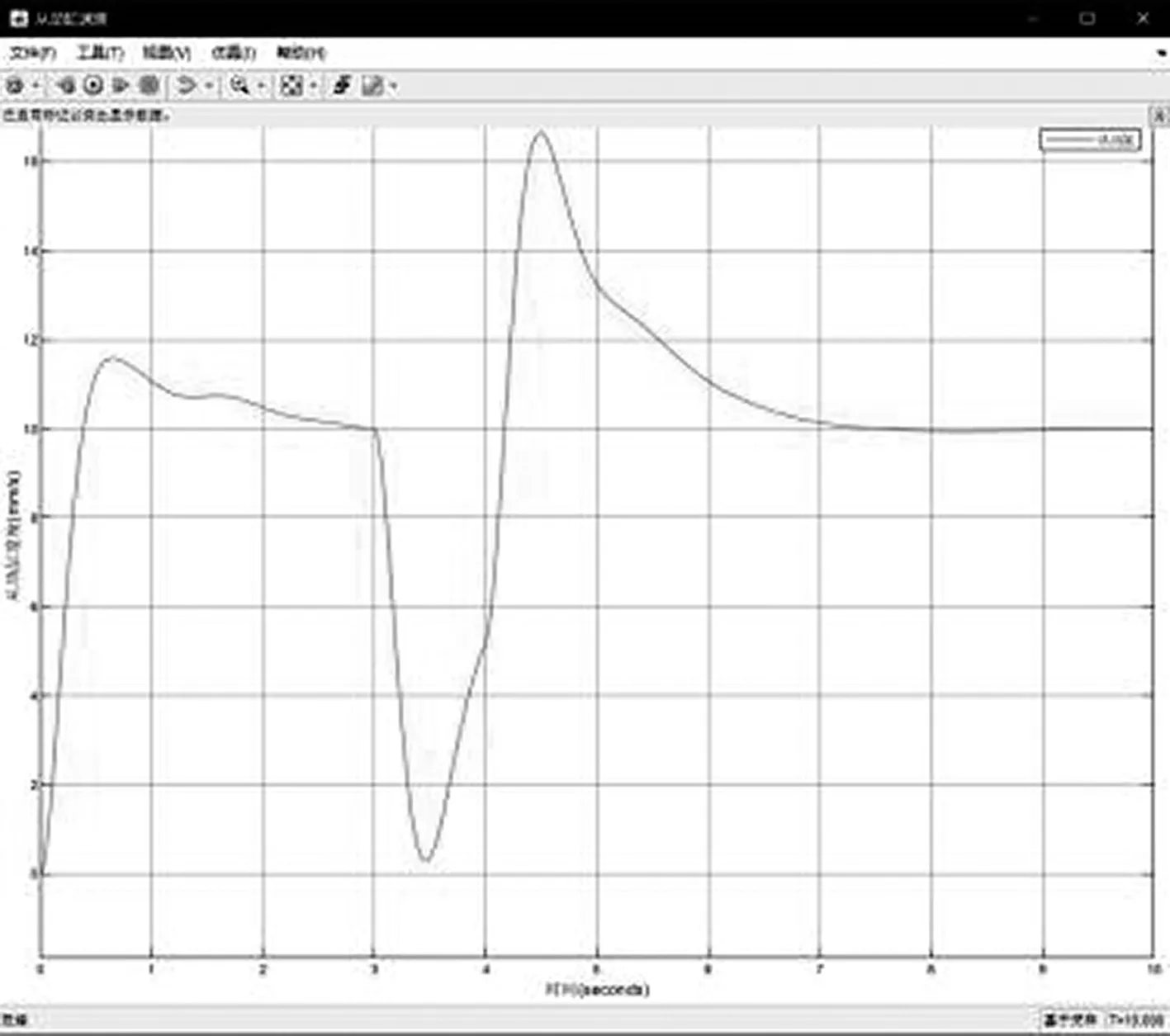
图11 模拟场景二从动缸速度变化曲线
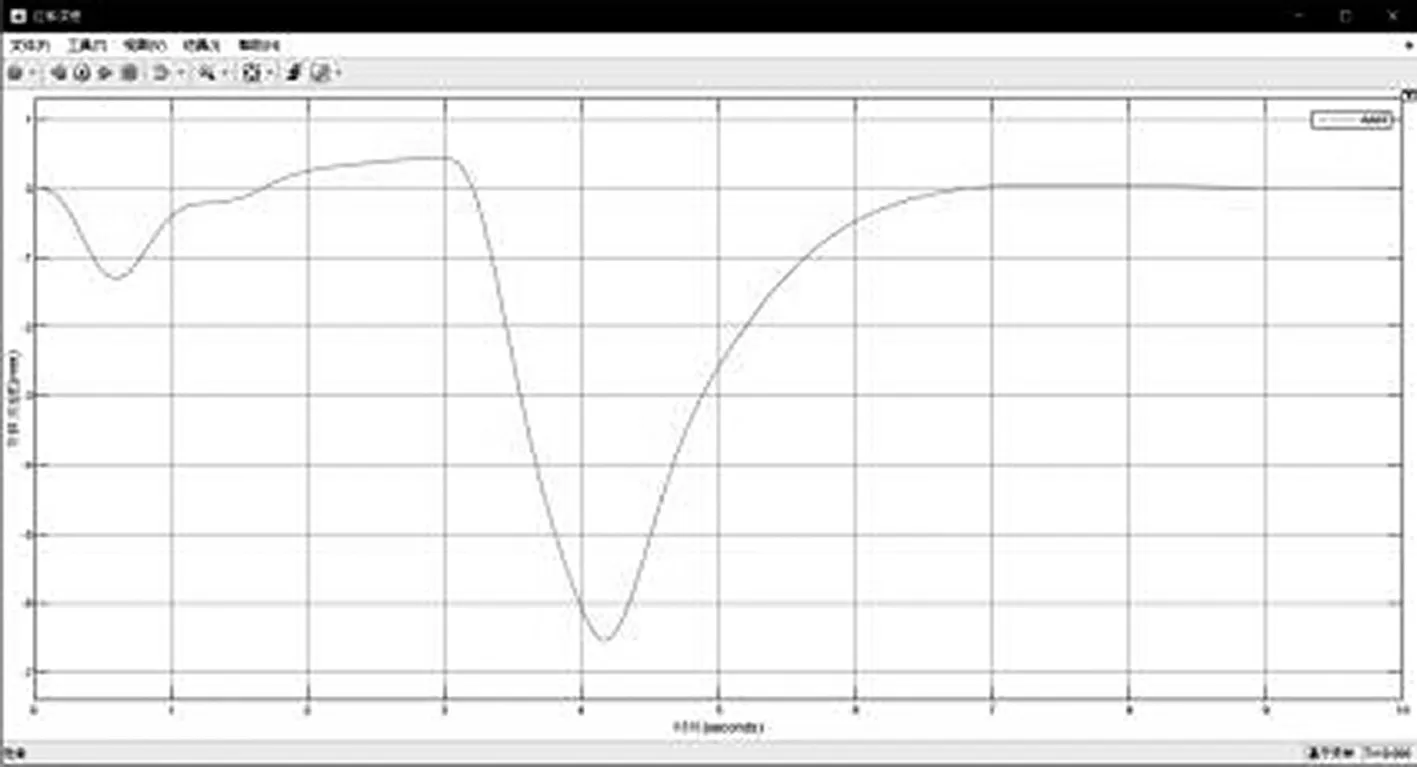
图12 模拟场景二双缸位移差曲线
通过设定仿真时间3 s时从动缸速度为零来模拟从动缸卡顿现象,仿真结果显示:PID控制算法能够更快速地在卡顿之后将位移差值缩小到0附近,几乎没有静态误差,与对比多段速同步调整算法相比,PID控制几乎不受随机干扰的影响。
3 结束语
通过对两种不同情景模式进行对比仿真可以发现,PID控制算法与多段速同步控制相比能够更好地利用系统动态过程中过去、现在和未来的主要信息,不仅超调量小,调速曲线更为平滑,振荡更少,抗干扰能力更强,同时能够有效消除静态误差,让双缸同步误差更趋近于零。
但必须说明的是,在无法获得系统传递函数时,PID控制算法在实际部署时对调试人员的经验有更高的要求,其P、I、D3个参数的调试比多段速同步调整算法更为繁琐,对不同的系统泛用性差,因此需要根据现场实际情况综合考虑。
