中空钢管混凝土叠合柱偏压力学性能研究

2021-03-17任庆新丁纪楠李明伦娄贺清

沈阳建筑大学学报（自然科学版） 2021年1期

任庆新,丁纪楠,李明伦,娄贺清

(1.沈阳建筑大学土木工程学院,辽宁沈阳 110168;2.沈阳建筑大学研究生院,辽宁沈阳 110168;3.沈阳市铁西区碧桂园房地产开发有限公司,辽宁沈阳 110021)

中空钢管混凝土叠合柱是由纵筋和箍筋构成骨架、核心部位配置钢管,并在钢管外部浇筑混凝土而形成的一种结构形式,是将钢筋混凝土与钢管有机结合起来而形成的构件,也可以看作钢管混凝土叠合柱的钢管中未灌注混凝土。相比于传统中空钢筋混凝土构件，内置空钢管可改善试件的刚度和延性，因此，这种构件具有抗弯刚度大、自重轻、施工便利、防火性好等特点,适用于桥梁结构中的桥墩、高层建筑中的大直径柱、各种支架柱以及送变点杆塔等结构。

目前,针对钢管混凝土叠合柱的研究已经比较完善,主要借助试验和有限元模拟,以截面形式、含钢管混凝土率、钢管与混凝土强度等为参数进行轴压、压弯等静力性能研究,考察其力学性能,分析受力过程中管外混凝土和钢管混凝土截面应力分布规律、钢管与管外混凝土及管内混凝土之间的相互作用,基于参数分析建议钢管混凝土叠合柱偏心受压的承载力实用计算方法[1-3]。关于中空钢筋混凝土柱的研究,主要集中在轴压性能[4-8]和薄壁桥墩抗震性能方面[9],关于中空钢管混凝土叠合柱的研究相对较少。基于此,笔者在已有试验的基础上,建立有限元计算分析模型,对中空钢管混凝土叠合柱偏压下的荷载-挠度全过程曲线进行分析,研究偏心率和内置钢管直径对其约束机理和承载力的影响,并结合叠加理论和极限平衡理论提出了偏压作用下的承载力简化计算公式。

1 有限元模型

1.1 模型参数

中空钢管混凝土叠合柱模型参数:高度H=1 800 mm,宽度B=200 mm,内钢管直径D=80 mm,钢管壁厚t=3 mm,混凝土保护层厚度为25 mm,钢管采用Q345B钢材,纵筋采用HRB335 8Φ12,箍筋采用HPB300Φ6.5@100,钢管外混凝土强度等级为C40,试件参数及构造如图1所示。

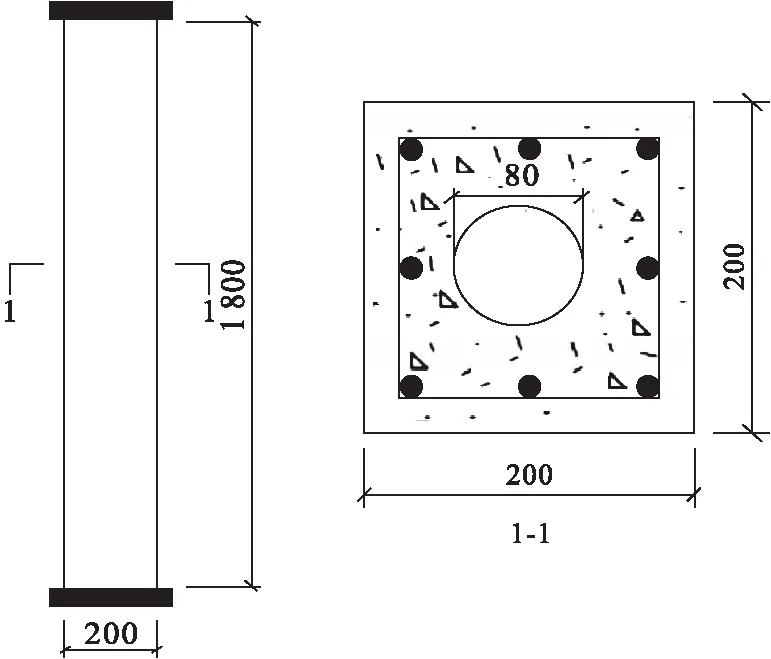
图1 试件参数及构造Fig.1 Dimensions and details of specimens

1.2 材料本构模型

笔者采用弹塑性模型来建立钢材本构关系,弹性模量和泊松比分别为206 GPa和0.3.钢管部分使用韩林海提供的五阶段应力-应变关系[11],钢筋部分使用双折线应力-应变关系,强化阶段弹性模量取0.01Es(Es表示钢材弹性模量)。混凝土本构采用塑形损伤模型,混凝土弹性模量Ec根据文献[12]取值,泊松比为0.2。箍筋外无约束混凝土采用M.M.Attard[13]提出的素混凝土本构关系模型,箍筋约束混凝土采用L.H.Han[2]提出的本构关系模型。

1.3 模型建立

构件有限元计算分析模型以及各单元类型如图2所示。采用结构化网格划分技术对各部件进行单元网格划分。

图2 有限元模型Fig.2 Finite element analysis model

钢筋内嵌于混凝土中,钢管与混凝土界面法向采用硬接触,切向采用库伦摩擦模型来模拟,摩擦系数取0.6[14]。将端板视为刚体,端板与混凝土端部采用绑定约束,端板与钢管端部采用壳-实体耦合,保证加载过程中钢管和混凝土与端板变形一致。试件加载点与端板结点区域的加载线耦合,对加载点约束X、Y方向的位移和绕Y、Z轴方向的转角,采用位移加载方式进行计算[15]。

1.4 模型验证

将有限元计算结果与文献[16]中的sc1、sc2和sc3试验结果比对。承载力对比结果见图3,图中Nue表示试验承载力,NuFEA表示有限元模拟计算承载力。破坏形态对比见图4。荷载-挠度曲线见图5,图中um表示侧向挠度,P表示荷载,同一参数进行两组试验。由图可知,有限元模型计算结果和试验结果吻合较好,因此笔者提出的有限元模型可以用来研究此类构件的受力性能。

图3 承载力对比Fig.3 Comparison of bearing capacities

图4 破坏形态对比Fig.4 Comparison of failure modes

图5 荷载-挠度曲线Fig.5 Load-deflection curves

2 有限元分析

基于上述有限元计算分析模型,对偏压下中空钢管混凝土叠合柱的工作机理进行研究。构件截面形式如图1所示,具体截面参数与试验试件一致,混凝土强度fcu=45 MPa,壁厚t=3 mm,钢管屈服强度fys=345 MPa,纵筋屈服强度fyl=400 MPa,纵筋直径为12 mm,箍筋屈服强度fyh=300 MPa,箍筋直径为6.5 mm,考虑钢管初始缺陷,初始偏心距按照H/1 000取值[13]。

2.1 荷载-挠度分析

中空钢管混凝土叠合柱参照钢筋混凝土的破坏形态,外围混凝土压溃时受拉钢筋没有屈服,为小偏压破坏;钢筋受拉屈服和试件达到峰值荷载几乎同时发生,为界限破坏;外围混凝土压溃时受拉钢筋已经屈服,为大偏压破坏。通过改变偏心距e,得到不同破坏模态下的荷载-位移(P-um)曲线如图6所示。图中关键点定义如下,Rc点:受压边缘纵筋开始屈服;Rt点:受拉边缘纵筋开始屈服;Sc点:钢管受压边缘开始屈服;St点:钢管受拉边缘开始屈服;P点:极限荷载Nu;U点:轴力下降到85%Nu。e=50 mm时,试件为小偏心受压破坏,破坏过程为受压区纵筋屈服→钢管受压区边缘屈服→构件达到峰值荷载→受拉区纵筋屈服;e=80 mm时,试件为界限破坏,破坏过程为受压区纵筋屈服→钢管受压区边缘屈服→受拉区纵筋屈服→构件达到峰值荷载→钢管受拉区边缘屈服;e=100 mm时,试件为大偏心受压破坏,破坏过程为受压区纵筋屈服→受拉区纵筋屈服→构件达到峰值荷载→受压区钢管屈服→受拉区钢管屈服。

图6 荷载-挠度关系曲线Fig.6 Load-deflection curves

从以上分析及图6可以看出,对于小偏心破坏试件,受拉区纵筋在试件达到其峰值荷载之后屈服;对于界限破坏试件,受拉区纵筋几乎和试件达到其峰值荷载同时屈服;对于大偏心破坏试件,受拉区纵筋在试件达到其峰值荷载之前屈服,因此可将受拉区钢筋的屈服作为组合柱不同破坏模式的标志。随着偏心距的增大,试件极限荷载减小,但延性显著提高,这是由于随着偏心距的增加,钢管逐渐由全部屈曲发展为受压单侧屈曲,部分处于弹性阶段的钢管使试件具有一定延性。

2.2 跨中截面混凝土纵向应力分布图

试件scl在受力过程中特征点Rc、P、U处跨中截面混凝土纵向应力分布情况如图7所示。由图可知,中和轴在加载过程逐渐向受压侧移动,混凝土受压区面积减小。 Rc点处由受压侧至受拉侧纵向应力逐渐降低且分布较为均匀;P点处角部混凝土应力值较大,且应力值随角部距离的增大而迅速减小。在试件达到极限荷载时,混凝土截面高应力位于压区角部和压区钢管处;随着跨中挠度的进一步增加,U点处混凝土角部和钢管两侧的应力值开始下降。

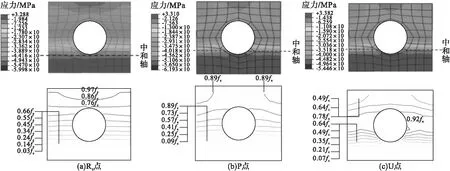
图7 特征点处跨中截面混凝土纵向应力分布

2.3 接触应力

接触应力即试件中钢管与混凝土之间的相互作用,反应破坏过程和约束机理。在钢管中截面选取代表点,点1位于钢管中截面受拉区最外边缘,点2位于钢管中截面受压区最外边缘(见图8)。

图8 接触应力位置Fig.8 Location of contact stresses

中空钢管混凝土叠合柱中截面代表点处P0-um关系曲线如图9所示。图中P0表示混凝土和钢管之间的接触应力,即外层钢筋混凝土对内钢管的约束作用,P0>0表示钢管与混凝土之间发生相互作用,P0=0表示钢管与混凝土的界面有分开趋势。

小偏心受压破坏试件的接触力-位移关系曲线如图9(a)所示。接触应力先增大后减小,压区钢管屈服先于混凝土被压碎。当压区钢管屈服时,由于钢管内部无支撑,因此压区钢管向内屈曲并与混凝土脱开;当拉区混凝土破坏时,钢管受拉侧并未屈服,且由于存在二阶效应,钢管拉区侧向变形增加,拉区的接触应力逐渐增大。

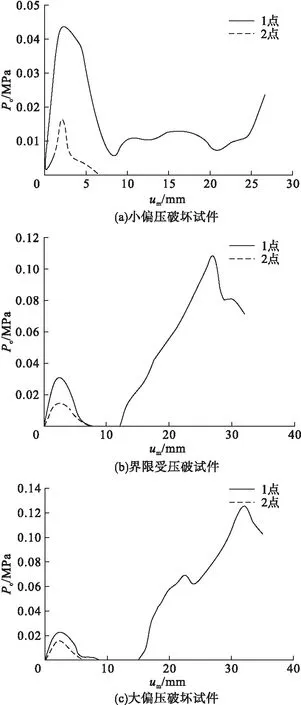
图9 不同破坏形式下接触应力-挠度关系曲线

界限受压破坏试件的接触力-位移关系曲线如图9(b)所示。相比小偏心受压试件,在初始阶段,接触应力明显降低,拉区混凝土破坏后和钢管脱开,内钢管拉区无混凝土约束,由于偏心距的增加,内钢管侧向挠度变形增加,因此变形后的钢管与拉区混凝土重新接触,由于压区钢管向内屈曲,压区钢管与混凝土脱开。

大偏心受压破坏试件的接触力-位移关系曲线如图9(c)所示。在初始阶段,受压区和受拉区的接触力低于界限受压破坏的试件,且由于偏心距的增加,当拉区混凝土破坏后,无约束的钢管侧向变形逐渐增加,与混凝土重新接触,且二者的接触应力随着偏心距的增加和侧向挠度的发展逐渐增大。

2.4 钢管直径对力学性能的影响

为分析内置空钢管直径对中空钢管混凝土叠合柱偏压性能的影响,笔者选取偏心距为50 mm试件进行研究,设置钢管直径D分别为60 mm、100 mm和140 mm。图10为内置不同直径钢管的中空钢管混凝土叠合柱荷载-挠度曲线。从图中可以看出,随着内置钢管直径的增大,试件受压区混凝土面积降低,因此极限荷载逐渐减小,当钢管直径由60 mm增加至100 mm和140 mm时,极限承载力分别降低了0.4%和5.8%。由于试件中含钢率的增加,刚度略微提高,钢管直径由100 mm增至140 mm时,试件刚度变化不大。

图10 钢管直径对荷载-挠度影响曲线

2.5 偏心率对力学性能的影响

图11为不同偏心率条件下荷载-挠度曲线。由图可知,偏心率对试件极限承载力的影响较明显,随着偏心率的增大,试件承受的极限荷载和刚度减小,当偏心率由0.2增至0.5时,极限承载力下降幅度最大,达到33%,极限承载力对应的跨中挠度不断增大,试件延性随着偏心率的增大而提高。

图11 偏心率对荷载-挠度影响曲线

3 压弯承载力计算

依据《钢管混凝土叠合柱技术规程》(CECS188—2018)[17],管外钢筋混凝土分担的轴力设计值按照《混凝土结构设计规范》(GB50010—2010)[18]中钢筋混凝土柱截面偏心受压承载力公式进行计算。当长细比大于22时,需考虑二阶效应带来附加弯矩的影响,笔者采用偏心距增大法考虑二阶效应对偏心受压承载力的影响。方形截面可按图12所示等效成工字型截面。

根据《钢管混凝土叠合柱技术规程》(CECS188—2018)[17],试件大偏心受压时,仅考虑轴力对外部钢筋混凝土正截面受压承载力的影响;小偏心受压时,轴力设计值在钢管混凝土与管外钢筋混凝土之间分配。中空钢管混凝土叠合柱在偏心受压条件下的承载力参考《钢管混凝土叠合柱技术规程》(CECS188—2018)[17],分为大偏心、小偏心两种情况进行分析。