基于线性互补问题的多体系统接触/碰撞动力学研究

张欣刚，齐朝晖，王 刚，国树东，吴志刚

(1. 青岛理工大学 理学院，青岛 266525; 2. 大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024;3. 大连理工大学 海洋科学与技术学院，辽宁 盘锦 124221)

随着智能机器人、航空航天等领域的发展，轻质化、柔性化、复杂化、快速化的机械系统得到了广泛的使用，同时也促进了多柔体系统动力学学科的蓬勃发展[1]。以航天科技为例，其空间结构往往以折叠状态固定在舱内，入轨后再逐步展开，如大型桁架式索网天线，大型太阳能电池阵,柔性抓取机械臂等[2]。为了控制航天器的重量，这些结构多为大型轻质柔性结构。这些柔性构件在展开过程中不仅呈现出大转动、大变形刚柔耦合的动力学特性，其部件也不可避免的要与周围环境或自身发生接触/碰撞[3]，由此产生的非光滑振动不仅给航天器的姿态控制带来较大的困难，甚至导致航天器的失稳[4]。因此，深入分析结构柔性以及碰撞、摩擦对系统动力学特性的影响具有切实的意义。

对碰撞的描述可分为两类：① 忽略碰撞的细节，认为碰撞在瞬间完成[5-7]；② 用弹簧模拟物体对变形的抵抗能力，用阻尼模拟能量耗散[8-10]。第一类方法又被称为离散分析方法，优点是简化了接触过程且计算效率高，缺点在于不能计算碰撞过程中碰撞力的大小以及作用过程，其线性补偿策略可能会违反摩擦接触时的能量守恒定律[11]。第二类方法又被称为连续分析方法，允许接触体在接触区域相互嵌入，接触力可表示为侵入量的明确函数[12]。其中Hertz接触理论是使用范围最广研究范围最悠久的接触力模型。文献[13]系统总结了Hertz接触模型的发展，并着重讨论了模型中阻尼系数的发展过程。

将多刚体系统中应用最为广泛的连续接触力模型直接引入到多柔体接触/碰撞动力学分析中并非完全适用[14]。连续接触力模型将接触力描述为变形量的明确函数，相当于引入一个本构关系。而柔体自身有其本构关系。引入连续接触力模型刻画柔体间的碰撞，相当于给系统叠加了本构关系，从而使得两者相互干扰：一方面，模型中刚度和阻尼参数的确定含有很大的不确定性[15-17]；另一方面，由于一次碰撞历程中相对速度可在较大的范围内取值，加之受到两类本构关系的干扰，往往会计算出负的接触力，从而与接触力的性质相违背。基于线性互补理论的非光滑动力学模型能够保证接触力的非负性，且能够高精度的求解持续接触状态下的接触力，不足之处在于需要区分不同的接触状态，且无法同时定性和定量的分析碰撞时刻的接触力演化过程[18]。

结合以上研究现状，本文首先分析了连续接触力模型在多柔体接触/碰撞分析中的不足，随后在非光滑动力学的体系下，将多柔体系统模型降噪[19]的思想引入柔体间动态接触力的建模与计算当中，建立了平均化缝隙与接触力之间的标准线性互补方程。这种互补关系可以综合考虑碰撞和平顺接触，在接触状态发生改变时不需切换模型。不仅保证了接触力的非负性，也在很大程度上简化了非光滑互补问题的分析和求解过程。

1 柔体间动态接触力模型

1.1 连续化模型

接触力可视为单面约束提供的约束反力，其重要力学特性是约束反力的单向性：沿缝隙函数gi增加方向的接触力值τi必须非负，而当缝隙函数gi大于零时τi必须为零。因此缝隙函数和法向接触力必然满足以下关系式

0≤gi⊥τi≥0

(1)

尽管上述关系符合客观事实，但由于缝隙函数本身与接触力并不存在明确的函数关系，因此我们仅能通过它定性的确定接触力是否为零，而难以确定其幅值。

为了刻画柔体间碰撞力的演化过程，一些学者将连续接触力引入到柔性多体系统接触/碰撞动力学中，例如应用很广泛的Lankarani和Nikravesh模型

(2)

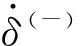
式(1)的一个特例是，当单面约束正在起作用时，由于缝隙函数及其一阶变化率均为零，因此退化为平顺接触时的线性互补关系

(3)

由动力学普遍原理可知，缝隙函数的二阶变化率与接触力存在函数关系，因此接触力可以被确定，大量算例也证实了这种关系的真实性。由此可见，平顺接触条件下不需人为设定接触力模型也可以高精度的求解接触力。事实上，连续接触力模型将图1(a)物体之间的瞬时碰撞抽象为图1(b)所示的等效系统。由图1可见，人为设定柔体之间的接触力模型相当于给系统叠加两个本构关系，从而带来了一定程度的干扰。

(a)

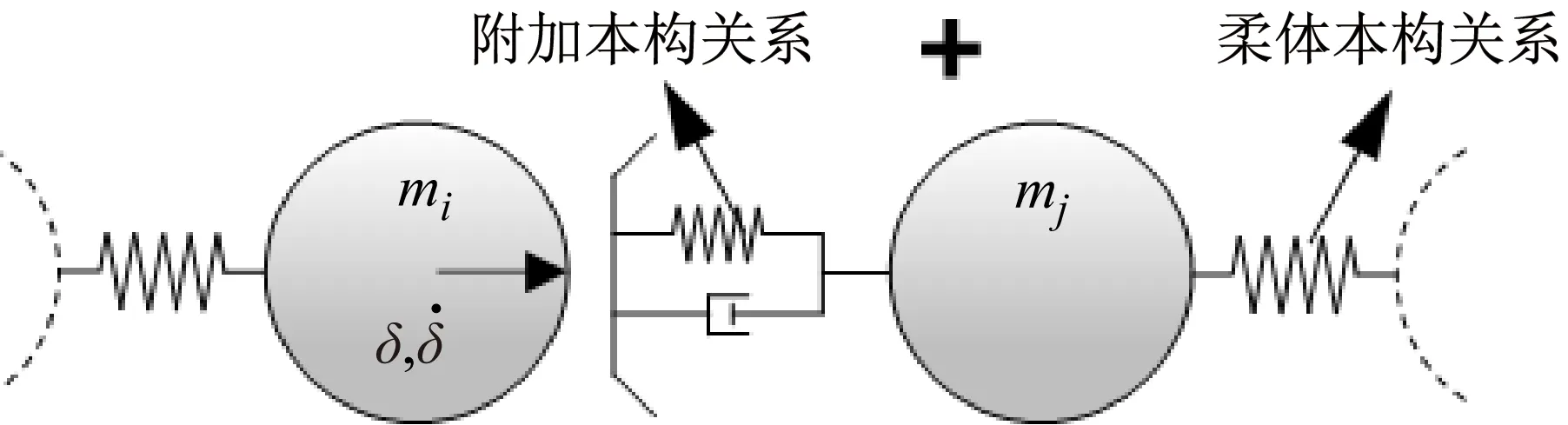
(b)图1 柔体间接触力模型Fig.1 Contact force model between two flexible bodies

1.2 互补问题的光滑化方法

类比库伦摩擦定律可见：一些物理上正确的数学描述往往无法用于数值分析。当所研究的系统无stick-slip运动状态的切换时，人们往往采用修正的库伦摩擦模型来代替。将间断函数连续化也是处理非光滑问题的一类被验证可行的方法。

类似地，将缝隙函数在短时间[t,t+h]内做泰勒展开，并保留到2阶,则ξ时刻的缝隙函数可表示为

(4)

(5)

由此可将接触力与缝隙函数的互补关系近似为

(6)

由于平均化缝隙函数表达式(5)中含有缝隙函数二阶变化率项，因此可确定接触力。经此近似以后的互补方程可以综合考虑接触与碰撞，且不必将接触过程人为的划分为多个状态。与式(6)等价的非线性方程形式为

(7)

2 接触/碰撞的线性互补方程

建立均匀化缝隙与接触力之间的标准线性互补方程，还需推导缝隙加速度与广义加速度之间以及广义加速度与接触力之间的函数关系。建立多柔体系统动力学方程的物理依据是虚功率原理，可表述为弹性体外力虚功率等于弹性体惯性力虚功率与弹性体变形虚功率之和

(8)

式中：r为物体内一点的矢径；σ和ε分别为该点处的广义应力和广义应变；f为作用在该点的外力。当给系统增加外力时，仅需计算该作用力的虚功率并叠加到系统虚功率方程中即可。

不考虑接触力时，系统的虚功率方程可由广义坐标q表示为

(9)

式中:M为广义质量阵;F为广义力阵。

接触力的虚功率可表示为

(10)

将接触点虚速度用广义速度表示，则式(10)可改写为

(11)

(12)

所有接触力虚功率之和为

(13)

式中

Kf=[Tf1e1,Tf2e2,…,Tfnen]

(14)

f=[f1,f2,…,fn]T

(15)

接触力对广义力的贡献即为Kff，如果式(9)所选的广义坐标独立，则系统动力学方程可由此写为

(16)

由式(16)，可将广义加速度由接触力线性表示

(17)

根据运动学关系，我们也总能将缝隙函数的变化率表示为广义坐标变化率的函数

(18)

(19)

综合式(7)以及式(17)～(19),并将其代入式(5),我们可以通过标准线性互补问题

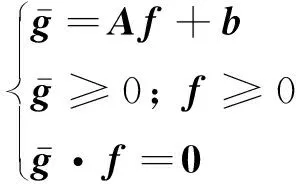
(20)

并通过求解其等价的非线性方程组(7)来求解接触力f，其中

(21)

(22)

求解式(20)得到接触力后，代入式(17)即可得到广义加速度。

用均匀化的缝隙函数与法向接触力建立互补方程，实际上是将突变的接触力进行了光滑化处理，当物体临近接触时接触力已经开始起作用，而当缝隙函数及其变化率均为零时，方程又可退化为平顺接触时的接触力方程。一方面能够解出接触力随时间的演化，另一方面严格满足互补条件，因此不会解出负接触力。

3 数值算例

例1：图2所示的弹性质量系统，各质量点均为mi=m=1 kg，弹簧刚度ki=k=104N/m。静止状态下间隙为零。左侧3号质点在外力作用下向左移动0.03 m，达到静平衡后释放并与右侧系统发生碰撞。分别采用弹簧阻尼模型以及所提线性互补方法进行数值仿真。弹性阻尼模型的等效刚度取140×106N/m3/2。

图2 弹簧质量系统Fig.2 Spring-mass system

为了进一步讨论连续接触力模型对柔体本构关系的影响，我们以Flores模型为例，分别计算不同恢复系数条件下的系统响应。图3分别给出了不同恢复系数、相同时刻不同恢复系数两种情况下的系统机械能时程曲线，图中cr表示恢复系数。

由图3(a)可见，恢复系数为1时为纯弹性碰撞，系统机械能守恒。但随着恢复系数的降低，在相同时刻，系统机械能并没有随着恢复系数的降低而降低，而是呈现一定的波动。图3(b)给出了相同时刻不同恢复系数条件下系统机械能的变化,更为直观了展示了这种波动。

除以上情况外，计算得到的恢复系数与预设的恢复系数也呈现了较大的差异，图4给出了不同接触力模型设定恢复系数与计算恢复系数的比较。

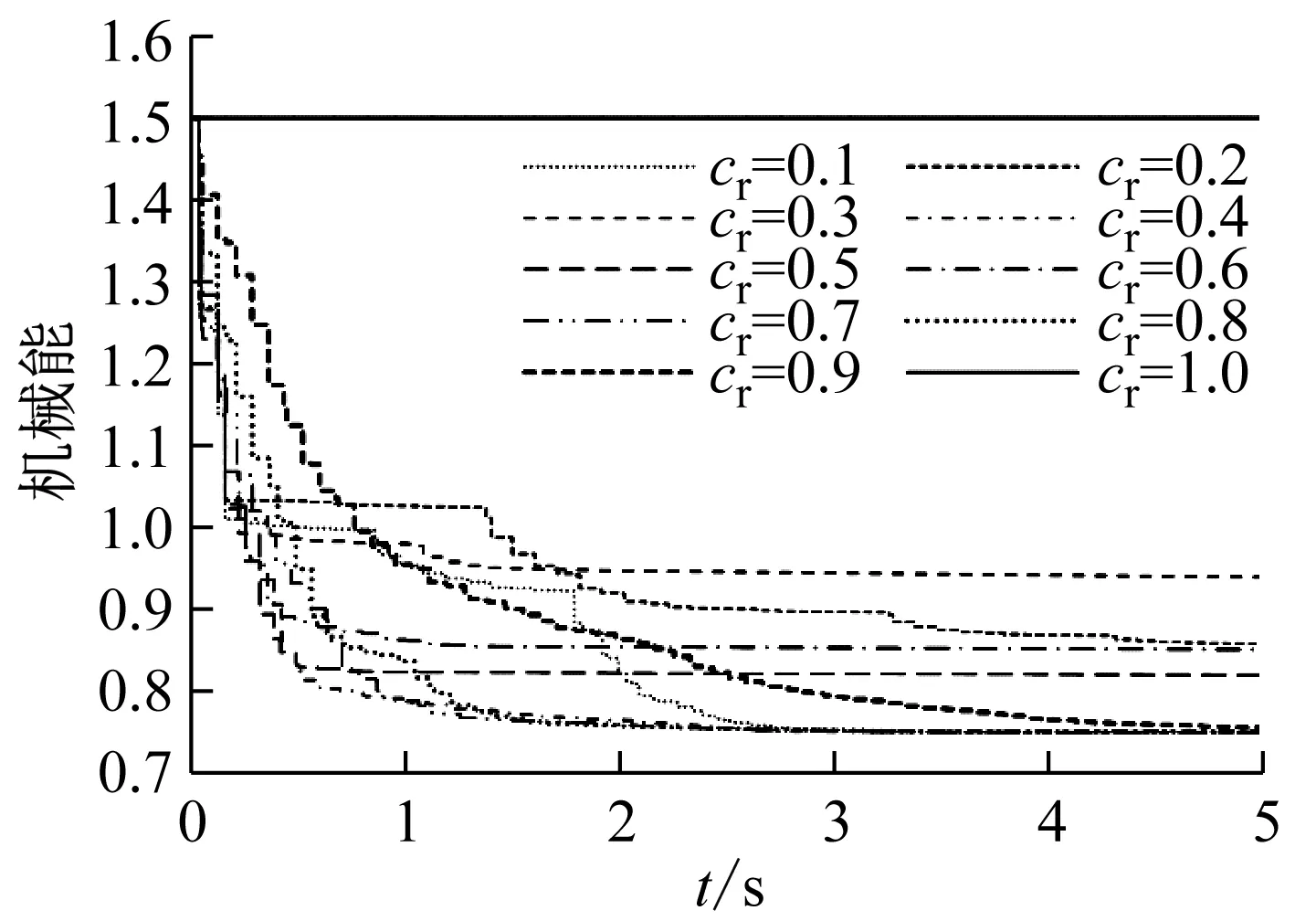
(a) 时程曲线

(b) 相同时刻不同恢复系数图3 系统机械能Fig.3 System energy

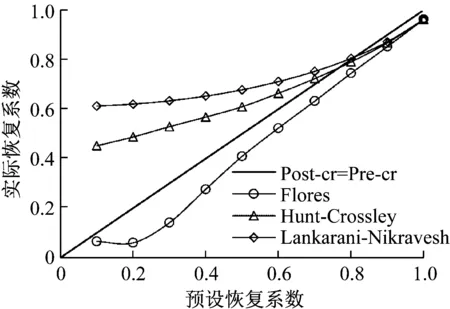
图4 预设与计算恢复系数关系Fig.4 Relation between the post and pre-restitution coefficients

对比图4以及文献[8]可见，Flores模型在计算刚体间碰撞时恢复系数与预设值吻合较好，但计算柔体间碰撞时就产生了较大的偏差。其余两种经典接触力模型[9,10]在计算刚体间高恢复系数碰撞问题时吻合较好，但计算柔体碰撞时也产生了一定的偏差。

除了以上两种情况外，将接触力模型引入到柔体间接触问题往往得到负的接触力。其主要源于两个方面：① 相对速度可在较大范围内取值；② 阻尼项中分母若含有恢复系数，则在低恢复系数时阻尼项绝对值被放大。如图5所示。其中各接触力模型及其适用范围可参照文献[20]的归纳总结。

由图5可见，对于分母中含有恢复系数的迟滞阻尼因子，在低恢复系数下其幅值就会被放大，加之相对速度在较大范围内取值，在低恢复系数情况下很容易计算出小于负1的阻尼项，如图6所示(Flores模型)。一次碰撞过程中接触力与侵入深度的关系如图7所示。当物体间相对速度为正(脱离)时，相对速度与初始相对速度之商为负，由于模型中阻尼项系数被分母中的恢复系数放大，则在物体脱离对方的时刻计算出了如图7所示的负接触力。

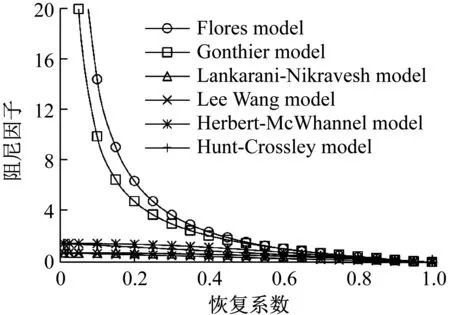
图5 阻尼因子与恢复系数关系Fig.5 Relation between damping factor and restitution coefficients

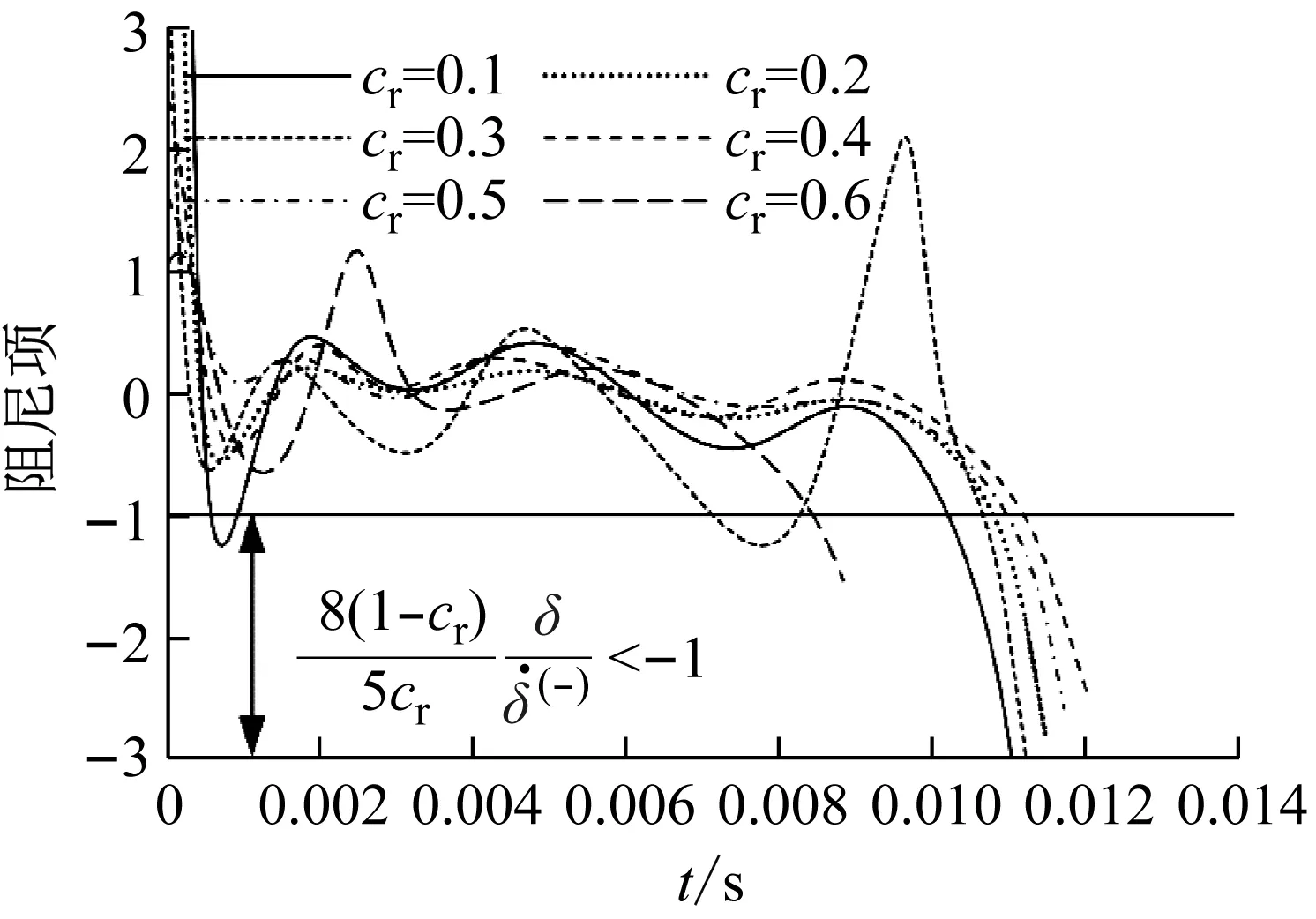
图6 阻尼项时程曲线Fig.6 Time plot of damping item

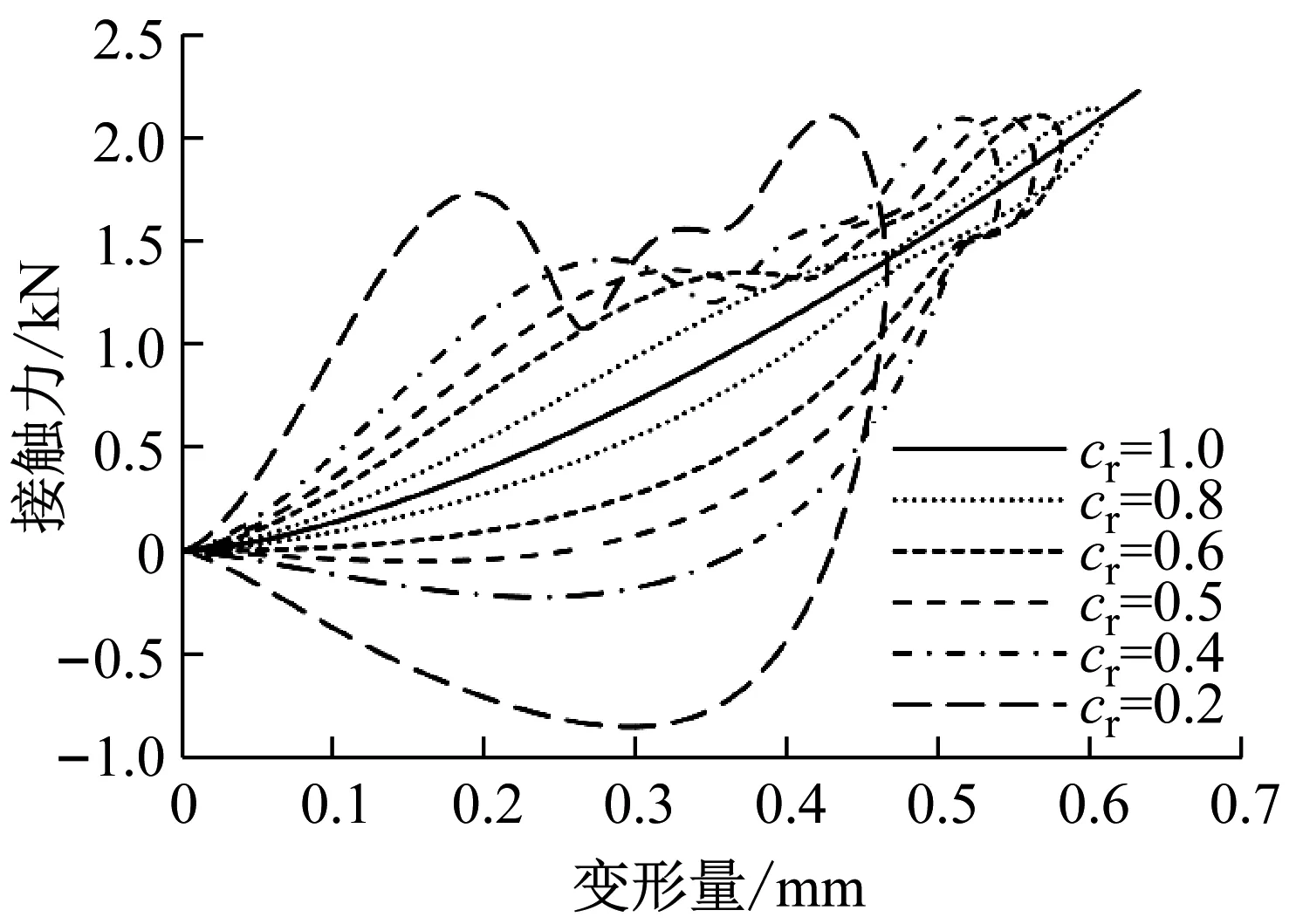
图7 接触力/嵌入量关系Fig.7 Contact force-deformation relation

采用所提线性互补方法时，实际缝隙函数与均匀化缝隙函数的关系如图8所示。由均匀化缝隙函数的表达式(5)可知，物体相互靠近时，缝隙函数大于零，其一阶变化率小于零，因此均匀化缝隙比真实缝隙要小一些，则在物体实际碰撞前的一个较短时间内接触力已经开始作用。并且h值越大，接触力作用的时间越早，接触力的峰值也随之降低。如图9所示。

图8 缝隙函数与均匀化缝隙函数关系Fig.8 Relation between normal gap and time-averaged gap

图9 不同参数h下的接触力时程曲线Fig.9 Time lapse of contact force with different h

图10给出了图9相应的接触力与实际缝隙函数的关系。与连续接触力模型相似，两者均可视为局部碰撞的连续化。但由于采用均匀化缝隙与接触力建立互补关系，因此物体在发生碰撞时也会有一定的嵌入量。另外，与冲量形式的摩擦碰撞线性互补模型[21-23]相比，优点在于可直接求解接触力的大小，且碰撞前后的状态依赖于柔体自身的本构关系，不必人为的设定冲量恢复系数。

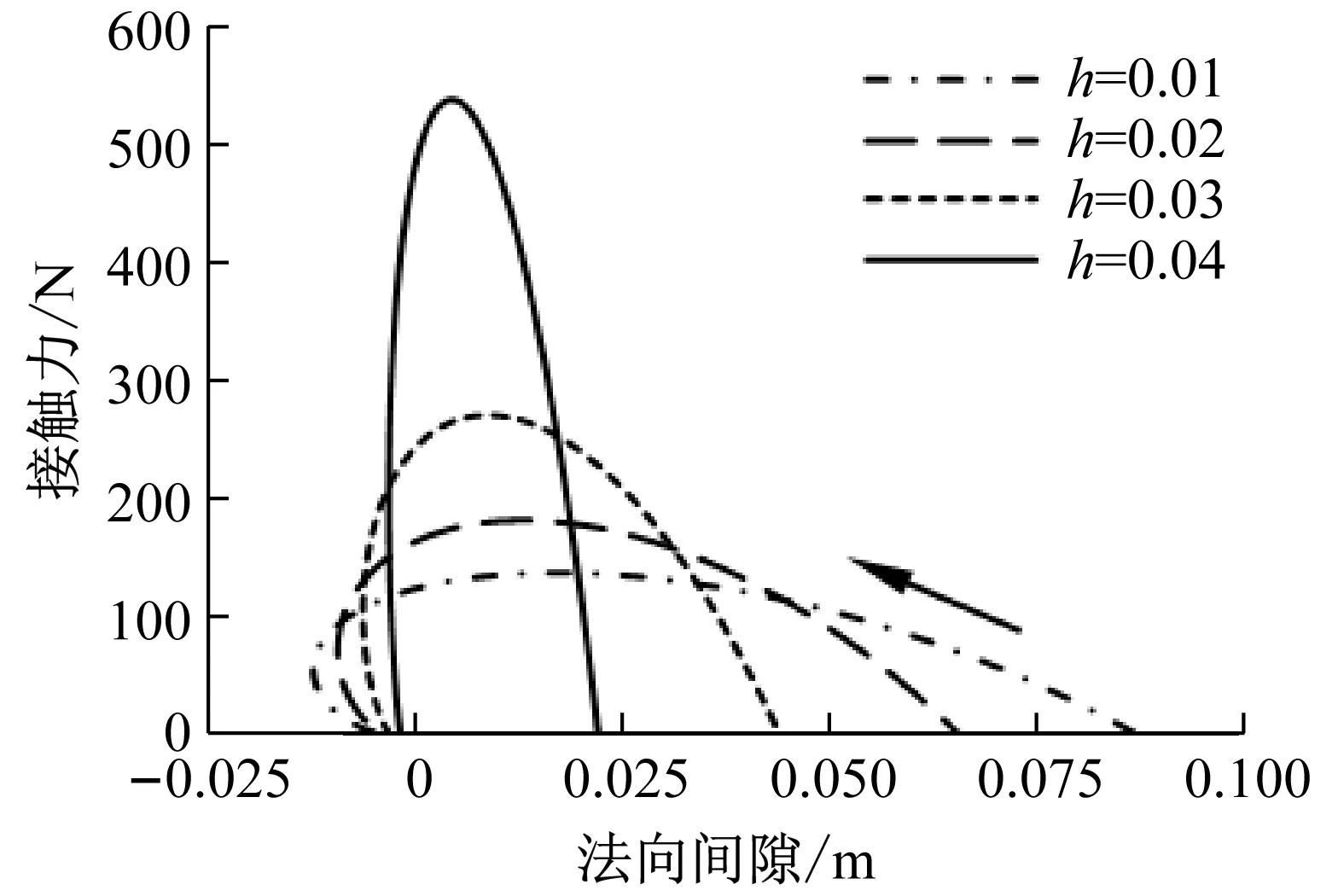
图10 接触力与缝隙函数的关系Fig.10 Contact force-gap relation

缝隙函数均匀化区间长度h对系统动力学响应以及接触力有着很大的影响，图11给出了不同光滑参数h下滑块3的位移时程曲线。

结合图11以及图9可见，均匀化区间长度h取值越大，接触力作用时间越长，碰撞效应将被磨平，位移曲线较为光滑。随着h值的减小，位移曲线逐渐吻合，更趋近于真实响应，但过低的h值也会使得所求接触力失真。建议h的取值应与碰撞时间在相同数量级。

图11 滑块3位移时程曲线Fig.11 Time lapse of the displacement of slider 3

实际上，除了碰撞力本身外，人们更为关心的是碰撞前后系统的动力学行为。图12给出了分别采用所提LCP方法以及连续接触力模型(CCF)计算的滑块3位移时程曲线以及接触力时程曲线，其中连续接触力模型中恢复系数取0.3。从中可见，除了连续接触力模型会计算出负接触力外，两种模型所求接触力略有差异，但系统动力学响应基本吻合。

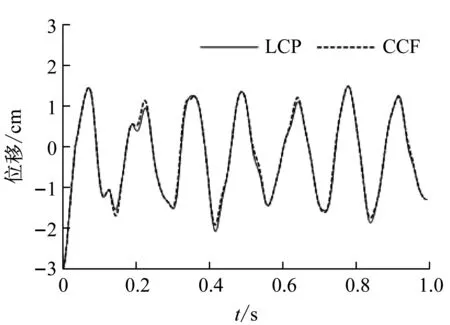
(a) 位移

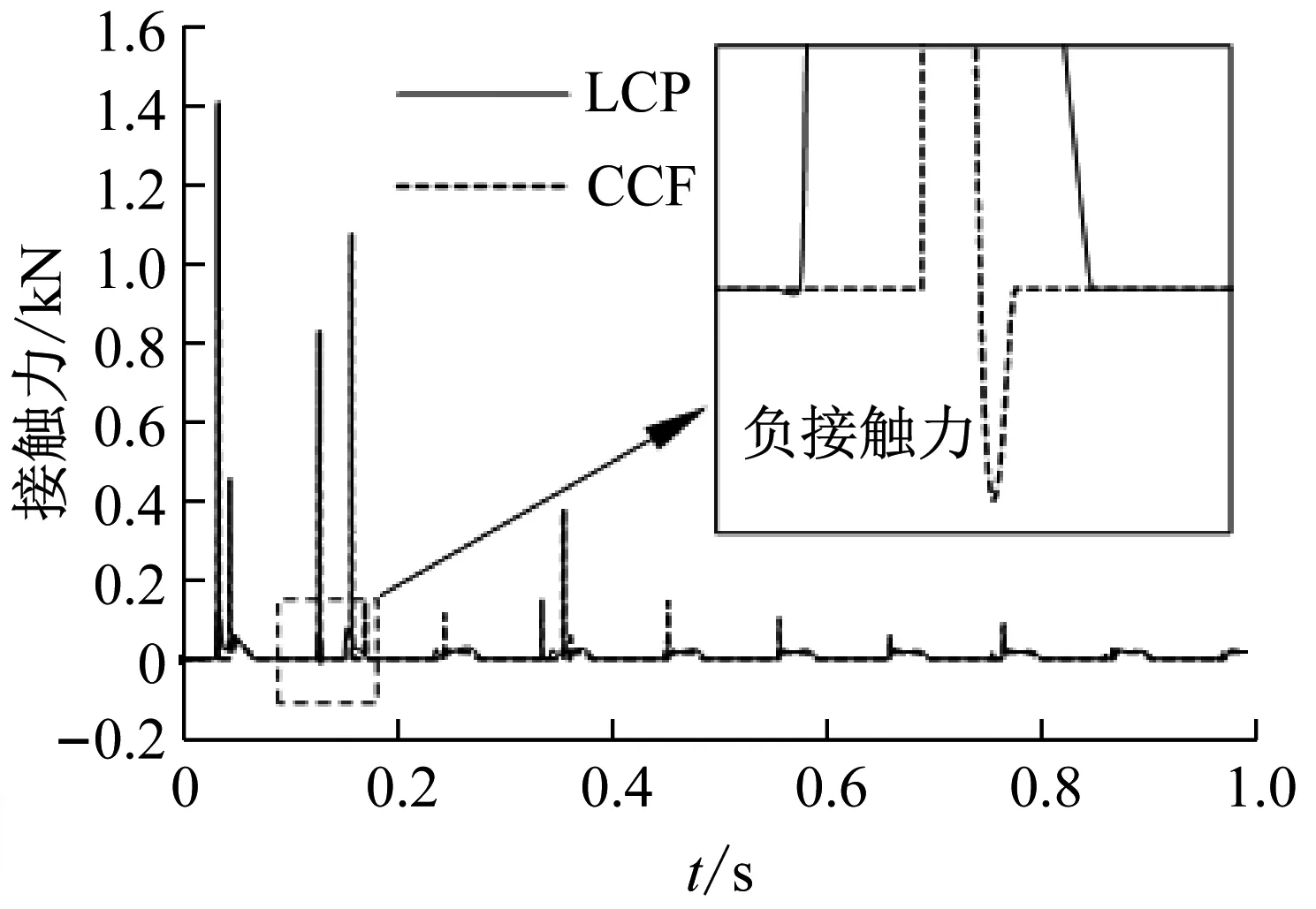
(b) 接触力图12 两种模型对比Fig.12 Comparison between CCF and LCP

例2本算例将给出所提方法在柔性多体系统接触/碰撞动力学中的应用。基于文献[19]所提的模型降噪方法以及文献[24]所提的大变形空间梁的共旋坐标法，将梁的广义应力修正为短时间内的平均应力

(23)

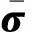
(24)

由于单元应变在共旋坐标系中为小量，因此式(8)可用单元刚度矩阵表示，并按照式(24)修改为

(25)

因此，修正后的节点内力为

(26)

式中：Ke为单元刚度矩阵；ue为单元局部参数，描述截面在单元坐标系下的位移和转动。

对于图13所示的柔性双摆机构，材料密度设为ρ=7 850 kg/m3，弹性模量E=2.1×109Pa，两根摆长均为L=2 m，截面积均为A=3×10-4m2。机构在重力加速度g=9.81 m/s2作用下，从水平静止位置落下并于刚性基础产生碰撞，假定平面光滑无摩擦。

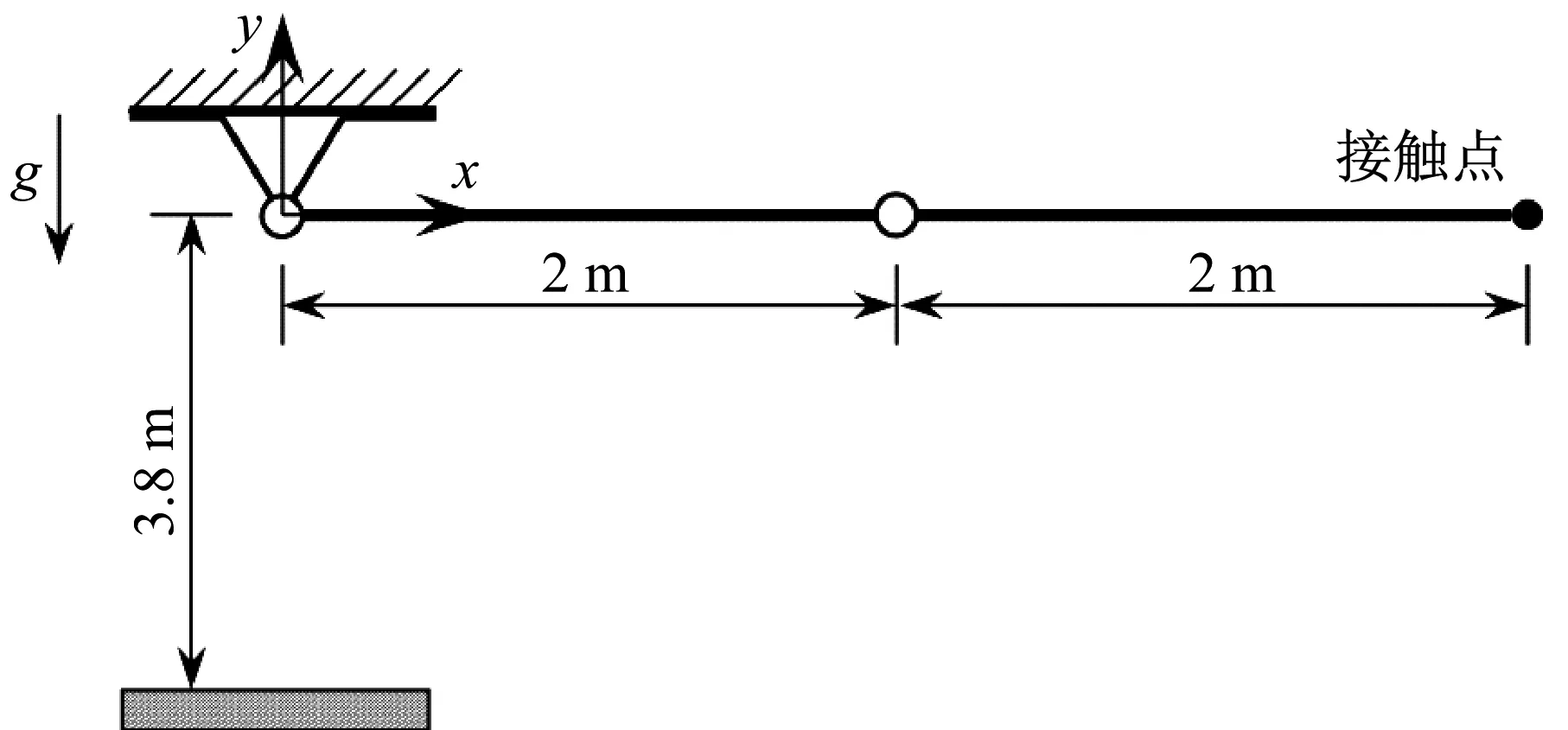
图13 自由下落并与基础碰撞的柔性双摆机构Fig.13 Free-falling flexible double pendulum mechanismimpact with foundation

采用MATLAB ode45常微分方程求解器对该问题进行数值积分，取精度控制参数εr=1.0×10-4和εa=1.0×10-6。得到双摆结构在不同时刻的构型图和碰撞力时程，分别如图14和图15所示。

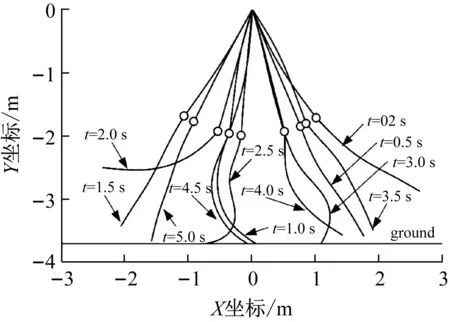
图14 双摆构型图Fig.14 Deformed configurations of flexible double pendulum

由图14和图15可见，当柔性双摆的材料刚度较小时(E=2.1×109Pa)，第二根摆在碰撞后变形很大。由于材料较柔，碰撞后杆端并没有弹离地面，而是进入平顺接触状态，沿平面滑动一段距离后脱离地面。

图15 接触力时程曲线Fig.15 Time lapse of normal contact force

多柔体系统的刚性以及接触非线性极大的增加了数值求解的困难，数值解的高频振荡也往往导致接触力求解失真。刚性积分器的算法阻尼往往不能有效地衰减高频振荡，往往通过在模型中引入少许线性阻尼或结构阻尼的方式进一步滤除高频振荡。采用文献[19]所提的模型降噪方法时可采用常规的积分器(如ode45)进行求解。此外，为了避免磨平碰撞效应，在滤除过高频率弹性振荡的前提下，模型中的降噪因子应尽可能的小，以提高数值解的精度。

4 结 论

为刻画柔体间动态接触力，选取当前时刻为起点的短时区间[t,t+h]内对缝隙函数进行均匀化，建立了均匀化缝隙函数与接触力之间的线性互补关系，该方法可综合考虑碰撞和平顺接触，不必在接触状态发生改变时切换模型，同时保证了接触力的非负性。为了降低高频成分对求解接触力的干扰，引入模型降噪方法滤除了过高频率的高频振荡成分，提高了数值求解的稳定性。

数值算例表明，所得结果在定性和定量两个方面都是合理的。该方法不仅适用于单点接触，同时也适用于柔体间的多点摩擦接触问题。将所提均匀化线性互补模型与模型降噪方法相结合，可成为求解大型复杂柔性多体系统接触碰撞问题的新途径。