基于改进天牛须算法的主汽温控制系统PID参数优化

仝家朋（华北电力大学 自动化系，河北 保定 071003）

0 引言

PID控制因简单可靠，在实际中应用非常广泛。在智能PID参数整定方面，有基于蝙蝠算法的设计[1]、基于H2函数的粒子群算法的设计[2]，优化方法众多。本文将天牛须算法（Beetle Antennae Search，BAS）用于PID控制参数优化。改进了BAS，把改进BAS应用于电厂主汽温控制系统PID参数优化中，并与粒子群算法、经验公式法的PID参数优化结果进行对比。

1 天牛须算法

BAS的计算过程是对天牛觅食行为的模拟。当天牛进行觅食时，其觅食策略是根据左右侧气味浓度来移动，从而找到食物。天牛有两只触须，当左边触须感受出气味浓度比右边强时，天牛就向左移动，否则就向右移动[3]。受此启发，食物气味就相当于适应度函数，天牛感受食物气味强度就相当于判断适应度函数的大小，天牛找到食物就相当于找到了全局最优值。

用公式描述BAS的觅食策略：用一个N维向量表示天牛的质心，天牛的两须位于质心的两侧，天牛的步长step与两须之间距离d的比值为一个固定值。天牛飞到下一步后，头的朝向是随机的，即右须指向左须的方向向量是随机的，定义如下：

式（1）中，rands(·)为随机函数；k代表空间的维度。获得方向向量后，定义左右须的位置如下：

式（2）、式（3）中，xl与xr分别为左右须的位置；xt为t时刻天牛的质心位置；d t为t时刻两须间距。此时便可以确定下一刻天牛的运动方向和距离，如下式所示：

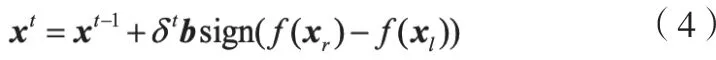
式（4）中，f(·)为被优化函数；δt是t时刻的搜索步长。初始时，大步长方便进行全局搜索，然后逐步减小步长值以进行精细搜索，如公式（5）所示：

式（5）中，g为迭代时步长的衰减系数。

在实际应用中，两须间的距离d t可随步长δt调整，如式（6）所示：

式（6）中，c为常数。

BAS的计算流程如下：①天牛初始位置为随机值；②用公式（1）和公式（5）更新须子方向和步长；③用公式（2）、公式（3）确定两须位置；④计算两须适应度值；⑤用公式（4）判断下一刻移动方向，更新天牛位置并计算新适应度值；⑥若循环到最大迭代次数或得到期望适应度值，则结束迭代过程，否则转回②，继续迭代。

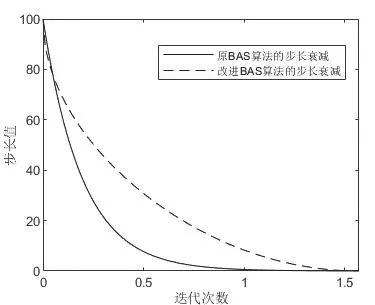
图1 改进前后BAS的步长下降趋势Fig.1 Declining step of BAS and improved BAS

2 BAS的改进

本文从两个角度对BAS进行改进：改进原BAS的步长衰减；加入了变异环节。

2.1 改进原BAS的步长衰减

原BAS是使用步长的固定衰减系数进行迭代，造成前期步长衰减过快、搜索精度低，中、后期步长衰减过慢、局部搜索效率慢[4]。经过多次试验，本文将原来的步长衰减公式变为式（7）的形式：

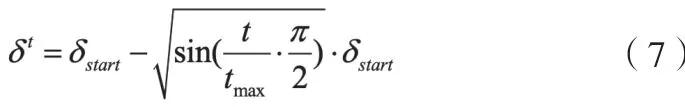
式（7）中，δt代表第t次迭代时的步长；δstart代表初始步长；tmax代表最大迭代次数。这样改进BAS与原BAS的步长下降的趋势如图1所示（设定δstart为100，tmax为158）。

从图1可看出，改进BAS的步长衰减在前期由快变缓，从而进行更多次大范围的搜索，更利于找到全局最优值的邻域；中期衰减较快，有利于算法快速缩小查找范围；后期衰减变慢，使算法查找更为精准。经实验测试，此下降趋势比原来的更符合算法需要。

2.2 加入变异环节

多次实验发现原BAS进行到最后阶段，其查找方式不足以找到最合适的最优值，常常陷于局部最优值。

本文在BAS中加入了变异环节，在算法的最后阶段发挥作用。该变异环节为：当步长值衰减到一定长度h时（即δt＞h时），算法中生成一个随机数作为概率，当概率小于一定值o的时候，公式（6）中的d t将按照公式（8）进行计算：

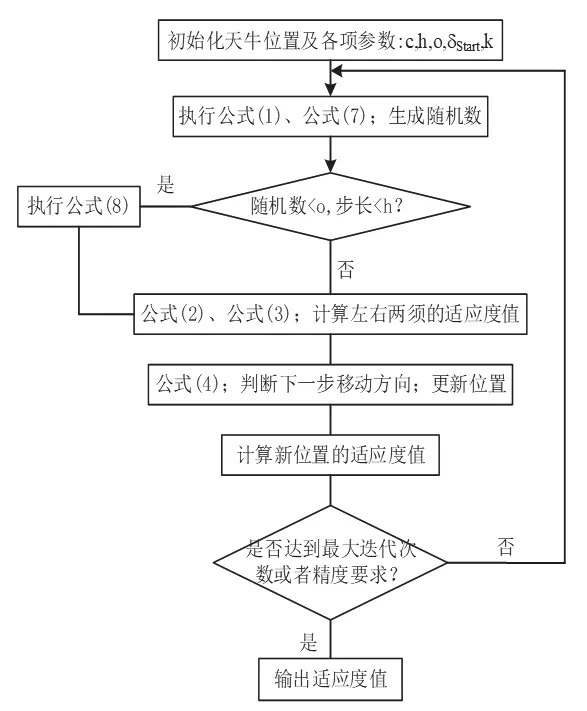
图2 改进BAS的计算流程Fig.2 Computing flow of improved BAS

式（8）中，rand(·)为随机函数。

该方法可以使算法拥有跳出局部最优的能力，扩大针对最终全局最优值的搜索范围。

2.3 算例测试

两次改进后，BAS计算流程如图2所示。

为了对比改进前后BAS的寻优效果，本文选取了8个测试函数来对算法进行测试[5]。这8个测试函数f1～f8分别为：Sphere、Rosenbrock、Rastrigin、Schaffers、Schwefel P2.26、Alpine、Ackley、Griewank。8个测试函数中前两个是单峰函数，可以检测算法的收敛速度；后6个是拥有大量局部极值的多峰函数，可以测试算法的全局搜索能力。

函数测试时，原BAS设定为：须子间距与步距大小之比c为2.5，每次迭代后步距衰减系数g为0.95。改进BAS设定为：c为2.5，变异概率o为0.3，限制值h=0.00004。在测试时，函数维度都设为二维，原BAS与改进BAS参数寻优初始位置都设为（5,5），步距δt初始值设为这8个函数的定义域范围两端值相减后绝对值的3%。例如，Rosenbrock函数对应的步距初始值为（|30-(30)|×0.03）。测试时，每个函数都独立运行100次，然后统计这100次结果的最好值、最差值、平均值、标准差，最多只统计到9位小数。迭代次数为3000时统计结果见表1，结果中的最好值加粗显示；改进BAS与BAS对应在函数f3、f8最优值随迭代次数的变化曲线如图3、图4所示。

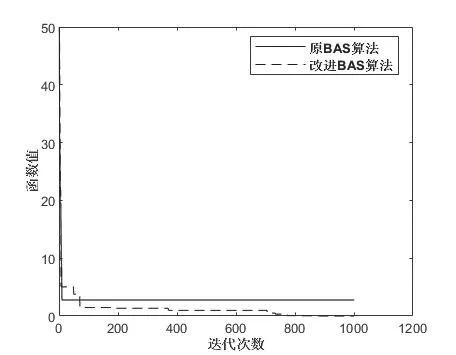
图3 函数f3最优值随迭代次数的变化曲线Fig.3 The curve of the optimal value of f3 follows the number of iterations

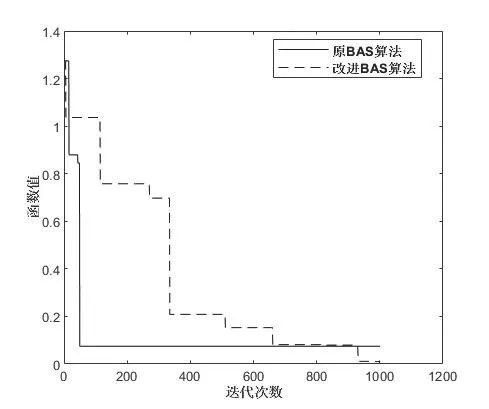
图4 函数f8最优值随迭代次数的变化曲线Fig.4 The curve of the optimal value of f8 follows the number of iterations

从表1可以看出，除了f1这样较简单的函数，其他函数上改进BAS都比BAS的表现好，更容易搜索到全局最优值且搜索效果更稳定。BAS在个别函数上最好值一项中能找到最优值0，但效果太不稳定，其对应的最差值表现的也更为不好，标准差较大。在这一点上改进BAS表现很好，而且随着迭代次数的增加，改进BAS的搜索结果也更好。从图3、图4中可以看出工作时改进BAS比BAS下降更快，搜索更快。

3 BAS优化主汽温系统PID参数

某电厂的主汽温控制系统[6]结构如图5所示，内回路采用PI控制，即比例积分控制器，外回路也采用PI控制，R为给定值。

表1 迭代3000次时测试结果Table 1 Test results at 3000 iterations

以该控制系统为测试系统。内环控制器参考前人的控制方式，其传递函数为kp1+ki1/s，其中kp1=10，ki1=0.0128；外环控制器的传递函数为kp+ki/s，使用改进BAS对外环控制器中的参数kp和ki进行寻找最优值，并与粒子群算法优化PID参数的方式、经验公式法设置PID参数的方式来进行对比。目标函数为能反映系统调节品质的绝对误差一阶矩积分ITAE，即：

利用经验公式法（临界比例度法）整定出的基本参数：kp=0.7399，ki=0.001327。

粒子群算法的设定为：迭代次数为100，设140个粒子，c1和c2均为1.4，惯性权重ω为0.7，单个粒子的维度为2，系统仿真时间为3000s，仿真步距为1s，最大速度Vmax为1，最小速度Vmin为-1，kp参数的寻优范围为[0,1]，ki参数的寻优范围为[0,1]。

改进BAS的设定为：迭代次数为2500，须子间距与步距的大小之比c为2.5，个体的维度为2，系统仿真时间为3000s，仿真步距为1s，kp参数的寻优范围为[0,1]，ki参数的寻优范围为[0,1]，步距δt初始值设为0.3，限制值h为0.00004，变异概率o为0.15。

基本BAS的设定值：迭代次数为2500，须子间距与步距的大小之比c为2.5，个体的维度为2，系统仿真时间为3000s，仿真步距为1s，kp参数的寻优范围为[0,1]，ki参数的寻优范围为[0,1]，步距δt初始值设为0.3，每次迭代后步距的衰减系数g为0.95。

本文基于Matlab2018a仿真平台来验证其有效性，电脑主频为2.60GHz，内存为8.00GB，CPU为i7-4720HQ。测试时，每个算法都独立运行100次，然后统计这100次结果的最好值、最差值、平均值、标准差，最多只统计到9位小数；另外，还统计这100次中在上升时间、超调量、调节时间3个指标上改进BAS比PSO好的情况。统计结果见表2，结果中的最好值加粗显示，经验公式法的标准差不进入比较，且经验公式的算法用时不进行测量。

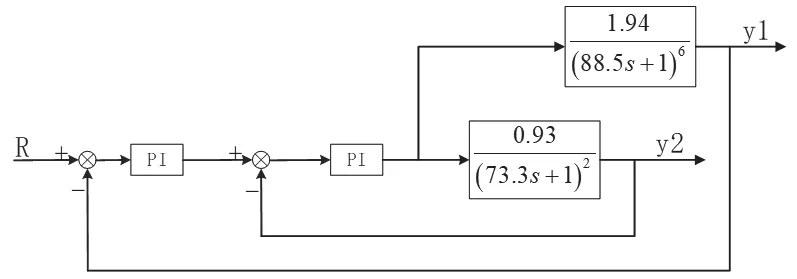
图5 主汽温控制系统结构图Fig.5 Structure drawing of main steam temperature control system

表2 4种算法的测试结果Table 2 Test results of four algorithms

从表2可以看出：经验公式法对应的响应曲线表现最差，其上升时间虽然短，但是超调量和调节时间都比较大；BAS算法对应的响应曲线最不稳定；改进BAS法对应的响应曲线的上升时间平均值比PSO法的略大一点，超调量平均值和PSO法的较为接近，但调节时间平均值比PSO法的要好，而且改进BAS对应的响应曲线在多次试验时表现更稳定。而在这100次中，改进BAS对应的响应曲线3个指标均比PSO好的情况发生了4次，其有两个指标比PSO好的情况发生了49次，只有一个指标比PSO好的情况发生了47次；在49次中，改进BAS对应的上升时间和超调量更好的情况发生了3次，上升时间和调节时间更好的情况发生了23次，超调量和调节时间更好的情况发生了23次。另外，从算法用时的角度看，改进BAS法的优化用时接近PSO法用时的一半（PSO算法此时迭代次数已到最少，再少则没有此时的搜索效果），较为可观。综上所述，改进BAS法优化控制器参数后，控制器表现更好，响应曲线表现更稳定，而且更有利于在算力较弱的设备上使用，更有利于在硬实时要求的环境中使用。

4 结论

本文在BAS的基础上进行改进，改变了原来的步长衰减趋势，在局部搜索时加入了变异环节。在主汽温系统控制器参数寻优后，改进BAS法对应的响应曲线表现更好，在3个指标上各有更好的优势。同时大幅度减少寻优用时，更有利于在算力较弱的设备上使用。当然，改进后的BAS也存在一些不足，较为明显的则是改进的BAS在高维度空间表现不佳。其进一步的改进方向可以为加入某些环节来增强该算法在高维度空间的搜索效果。