基于去相关化的低秩矩阵分解对口语能力的评估方法

林思岑

(西安医学院 外国语学院, 陕西 西安 710021)

0 引言

近年来，计算机辅助语言学习(Computer Aided Language Learning，CALL)作为一种提高非母语学外语口语能力的方法受到了广泛的关注。为了使CALL系统提供有用的辅导反馈，需要一个自动匹配的评分系统来评估非母语学生的发音质量、流利性和特定错误。

流利度评分系统一般由语音自动识别、流利度特征提取和评分模型组成。在流利性特征提取中，假设与外语口语流利性高度相关的特征被计算出来[1-3]。例如，长静默时间、每秒字数和交流持续时间是最常见的流利性特征[4]。评分模型是训练模型参数，将输入的流利性特征映射到相应的真实得分，然后用于预测输入话语得分的分类器。评分模型最常用的算法是线性回归[2]、支持向量机(SVM)[5-6]或高斯过程[7]。

分数建模是一个一般的有监督学习问题。因此，为了使模型得到可靠的训练，必须提供正确的真实分数作为目标输入。然而，要从人工评分的分数中获得正确的基本事实分数并非易事，因为这些分数包括由于人工评分的主观偏见造成的变异性。例如，每个人工评分可能会给相同的话语分配不同的分数。接着，通过消除人工评分的主观偏见来估计基本真实分数。最常用的方法是平均法，它通过平均有偏的分数来估计基本真实分数[8]；另一种是投票法，它基于多数人的意见[9]。

尽管平均和投票在实践中得到了成功的应用，但考虑到人工评分的偏见和评分模型度量，比如皮尔逊的相关性，关于它们是否能产生可靠的基本真实分数的问题仍然存在。因此，提出了一种基于去相关惩罚低秩矩阵分解的估计方法，并且本研究为了使结果更加准确，同时考虑了人工评分的主观偏见和皮尔逊的相关性。

1 基于深度神经网络的评分模型

1.1 深度神经网络模型结构

在此采用深度神经网络(Deep Neural Networks，DNN)作为评分模型。DNN是一种具有多个隐含非线性层的前馈神经网络[10]。对于输入流畅性特征向量x，每个隐藏层通过应用仿射变换和非线性映射将其输入向量从下一层转换到上一层，如式(1)-式(3)。

z0=x

(1)

y(l+1)=W(l)z(l)

(2)

z(l)=σ(y(l))

(3)

式中，W(l)表示l层的权重矩阵；σ(·)表示非线性激活函数。在最后一层中，softmax用于获得输入特征向量xt的第ith类si的概率，如式(4)。

(4)

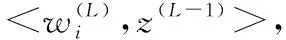
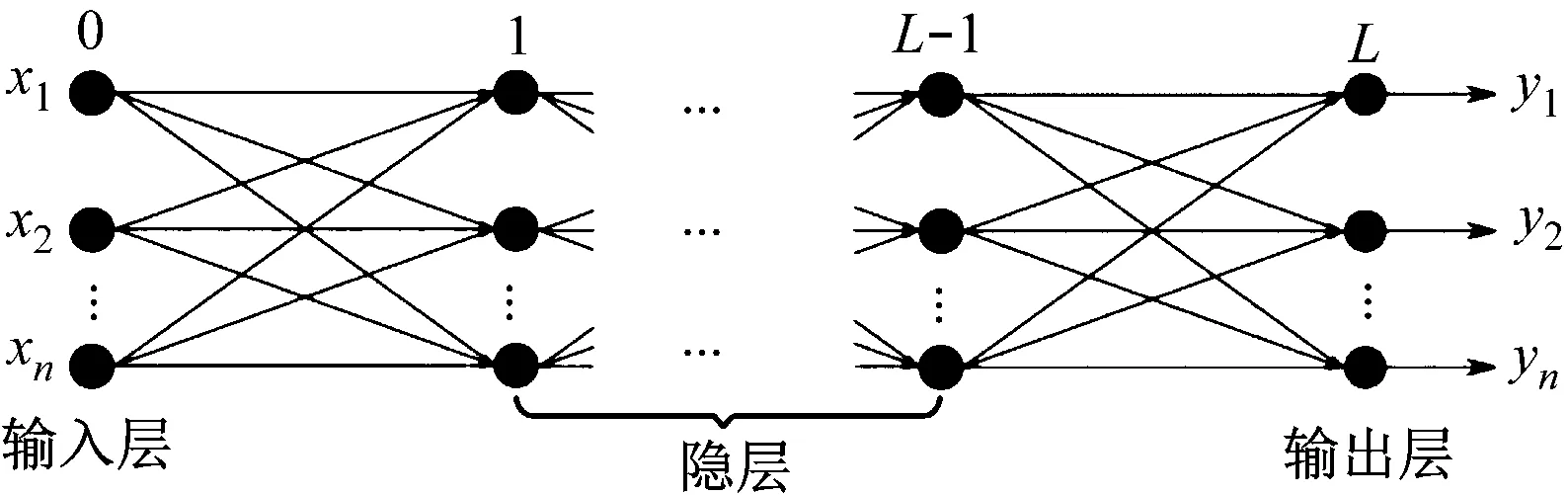
图1 DNN网络架构

1.2 训练语料库

为了训练基于DNN的评分模型，必须提供输入-输出对，(x1,y1),…,(xn,yn),其中xi是外语口语的流利特征向量，而yi是对应的真实分数。特征xi是由原始波形的流畅性特征提取计算的，如图2所示。

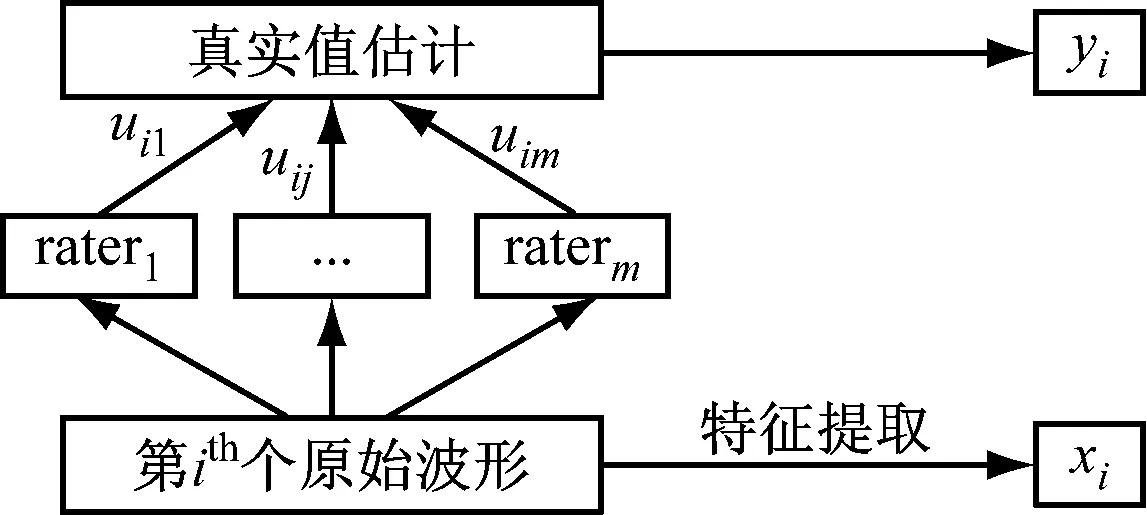
图2 训练语料准备程序

基本的真实分数yi通常是从m个人工评分的得分(ui1,ui2,…,uim)中获得。通常的估计值平均，如式(5)。

(5)

式中，uij表示第ith个话语的分数，由第jth个人工评分来评定。

1.3 评分模型度量

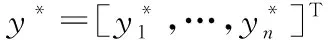
(6)

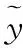
(7)

2 真实值估计问题

在这一节中，主要讨论真实值估计问题。

2.1 进行真实值评估的目的

在外语口语流利性评分模型中，由于设计了一个评分标准，并训练了人工评分员，使他们的评分之间保持高度的相关性，因此有时忽略了基本事实的估计问题。然而，评分者的评分存在分歧，为了训练DNN等计算评分模型，必须为每个输入特征确定一个单一的评分。

2.2 口语流利性评分中的基本事实估计问题

对于给定的人工评分矩阵U，其中(i,j)-th元素表示第j个人工评分分配的第i个话语的得分，如式(8)。

(8)

真实值估计的目的是寻找一种将(n×m)矩阵映射到n维向量y∈Rn的变换，该向量表示n个话语的估计真实得分。从这个意义上讲，式(5)中的传统平均值可以重写，如式(9)。

y=Um

(9)

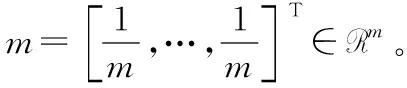
2.3 真实估计中的平均问题

在这项工作中，考虑了两个与使用平均值作为外语口语流利性得分的基本真实值估计有关的问题：(a)人工评分的主观偏见；(b)皮尔逊的相关度量。

首先，平均意味着在人工评分的解释中没有主观偏见，分数是在相同的标准下评分的，然而，很自然地假设每个人工评分都有特殊的不平等偏见；第二，平均不考虑皮尔逊估计的真实得分和人工评分的得分之间的相关性。这种相关性是一个重要的衡量标准，因为如果人工评分的得分之间的平均相关性为1.0，就不必估计基本事实。所以根据这些内容可知，期望估计的基本真实分数与人工评分的分数显示出高度的相关性。

3 解相关的低秩矩阵分解

在这项工作中，假设人工评分的得分矩阵U由人工评分的偏差向量w∈Rm和潜在得分向量y∈Rn相乘确定，如式(10)。

U≈ywT

(10)

换言之，假设Uij是由第j个人工评分的偏倚wj与第i个潜在得分yi的多重叠加来确定的。

因此，本研究的目标是将矩阵U分解为w和y，然后将y用作估计的真实分数。为了进行分解，将分数之间的去相关作为惩罚项，以最大限度地提高皮尔逊在估计的真实分数y和人工评分的分数U之间的相关性。

3.1 约束条件低秩矩阵分解

(11)

式中，损失函数L(γ,w,y)由重建误差和解相关惩罚项定义，如式(12)。

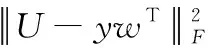
(12)

式中，γ控制解相关的贡献；R(y)测量估计的基本真实得分和人工评分得分之间的平均解相关，如式(13)。

(13)

式中，corr(Ui,y)表示第ith列向量Ui和y之间的皮尔逊相关性。另外，引入了非负归一化约束，例如0≤w≤1，因为流利度得分和人工评分的偏倚值是非负的，并且偏倚在0和1之间归一化。

3.2 对提出方法平均

从提出的方法的角度来看，常规平均的方法可以看作是本研究提出方法的一种特殊情况，其中w初始化为1n=[1,…,1]T和γ=0，那么w是固定值，所以式(11)可以改写，如式(14)。

(14)

3.3 随机投影梯度下降

在这项工作中，使用随机投影梯度下降(stochastic projected gradient descent，SPGD)算法来解决式(11)中的优化问题。虽然该算法较为简单，但对于合并约束条件是有效的。下面描述本研究中使用的SPGD算法，其中η是学习率。实验是通过使用Theano工具包实现的。

4 实验结果

在这一部分中，主要对提出的模型进行测试和结果评估。

4.1 实验环境和数据集

本研究的实验环境是在一台Windows 7 64位操作系统，16GB内存，Intel I7 3.5Ghz处理器的台式机上，使用的显卡为英伟达GTX 1080。实验采用的是Python 2.7语言进行数据处理。实验的数据集为FranÇis数据集[12]，该数据时长232小时，数据集包含经济，娱乐，新闻，口语，数字等法语语音，语音数据集共有404人参与录制(法国、加拿大、非洲等地的法语母语)平均每人录入392句；其中女性193人，占比48%。采用其中的80%数据作为训练集，剩下来的20%数据作为测试集，如表1所示。

表1 数据集中例句内容实例

每句话都由五位法语专家按1到5的比例打分。为了保持评分者之间的一致性，设计了评分量表，如表2所示。

表2 人工评分指南

每个人工评分的得分分布，如表3所示。

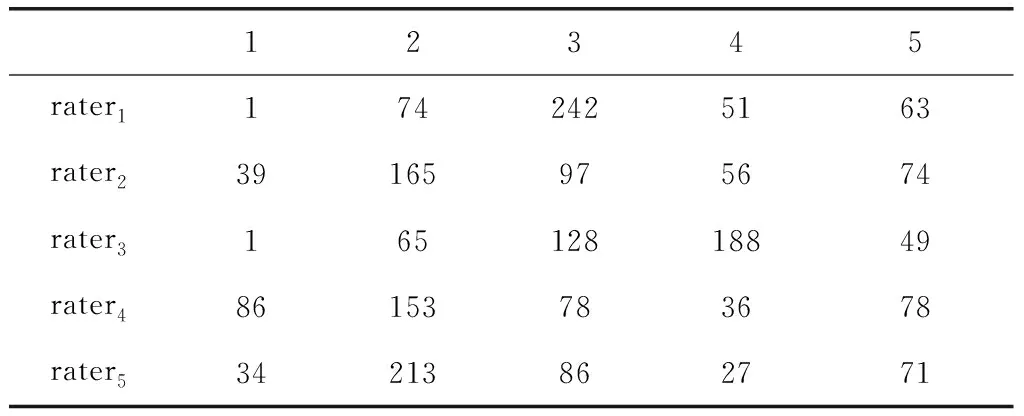
表3 人工评分的得分分布

评分之间的皮尔逊相关性，如表4所示。

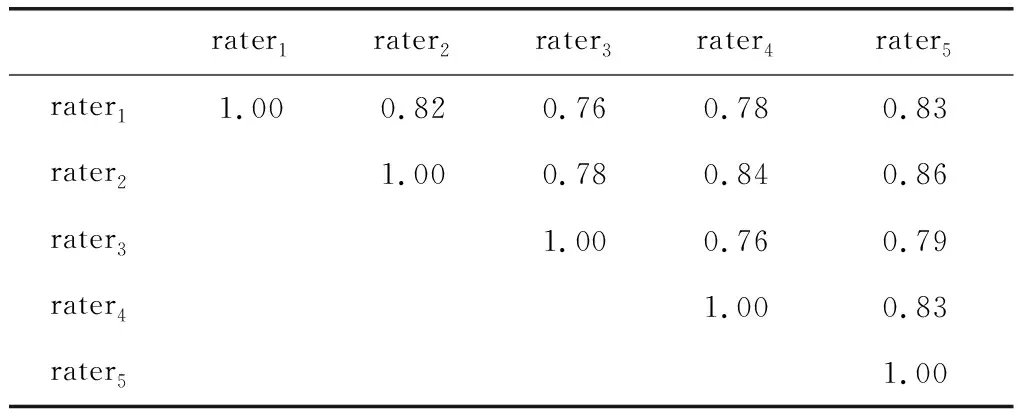
表4 等级间皮尔逊相关

(15)

实验中评估的估计方法，如表5所示。

“基线”是指传统的算术平均，“CASE-I”是平均方法，但以数值方式计算；“CASE-II”通过最大化皮尔逊相关度来估计基本真实得分；“CASE-III”通过消除人工评分的偏见和最大化皮尔逊相关度来估计得分。

表5 评估估计方法(w0=[1,…,1])

4.2 结果与评估

评估结果，如表6所示。

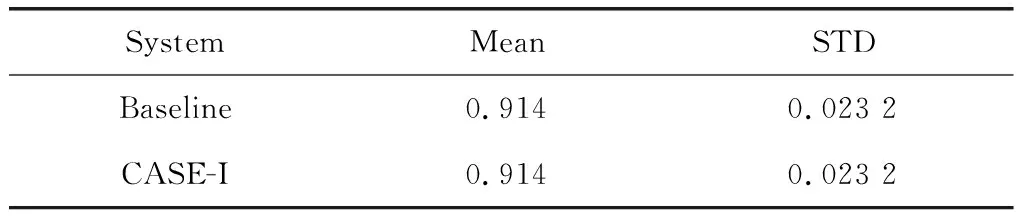
表6 评估结果

“Baseline”和“CASE-I”的性能相同，这意味着“Baseline”方法是该方法的一个特例。

改变γ值提出的方法的结果，如表7所示。

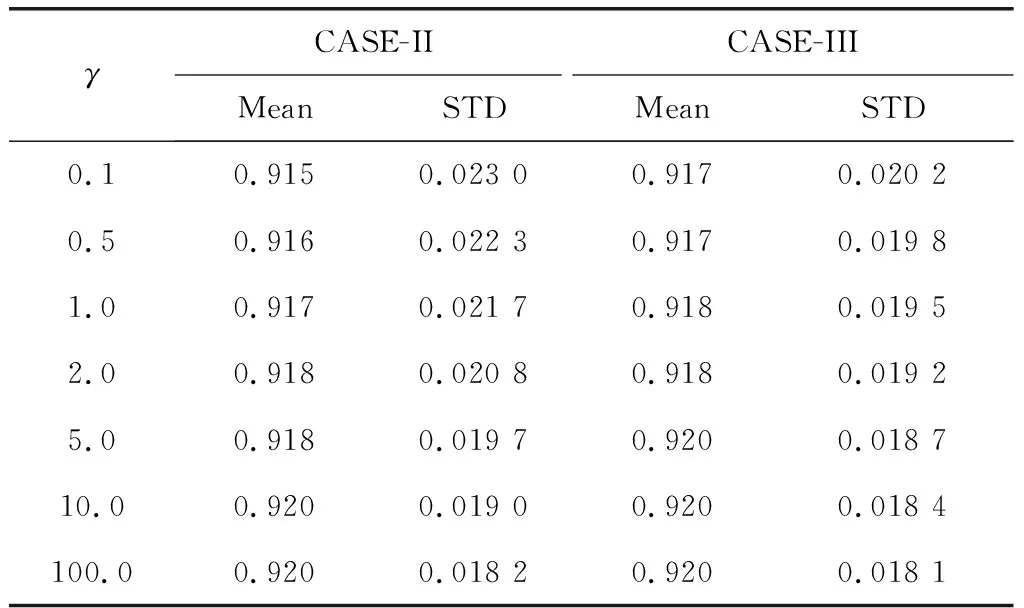
表7 提出方法的性能评估结果

可见，平均相关系数从0.914增加到最大值0.920，标准差从0.0232减小到0.01822。它还表明，“CASE-III”的表现略好于“CASE-II”。这意味着消除人工评分的偏见有助于增加平均相关性。虽然改进的幅度不大，但结果表明，该方法有助于提高估计的真实有效值的相关性，并减少估计的真实得分的变化。

4.3 人工打分的偏见归一化

表8 人工打分权重

从表中可知，rater3相对于他人表现出较高的偏向性，即rater3的得分高于他人，这与表3所示的得分分布有关。

5 总结

本文提出了一种基于约束条件的低秩矩阵分解的法语口语流利性得分的基本真实值估计方法。所提出的方法提供了一个通用的框架，用于消除人工评分的分数偏见，并包含其他信息，如皮尔逊的相关性。本研究还表明，传统的平均方法可以作为一个特殊的情况下提出的方法。

该方法的性能优于传统方法，但改进不大。因此认为其中一个原因是矩阵分解中缺乏非线性。因此，在未来的工作中，将引入非线性因素来分解人工评分的评分矩阵，并评估一个大规模的评分语料库。