边光滑有限元-边界元耦合法计算二维瞬态涡流场

王洋洋，蒋兴良

(输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044)

在瞬态涡流场研究中，常用的数值计算方法有积分法[1-2]、有限元法[3]、边界元法以及有限元边界元耦合法[4-7]. 虽然传统有限元法(FEM)[8]作为最成功的数值方法之一，已被广泛用于解决工程和科学的各种实际问题，但是因为其有固有的缺点，如剖分网格密度以及计算阶数的复杂程度都对有限元计算精度影响非常大. 单元数量的增加，及其插值函数精度的提高，才能得到更精确的数值解. 特别是在某些复杂的设计优化实例中，有限元法需要重复多次进行网格剖分以及重要部分网格加密操作，这不仅增加了设计的难度，而且还降低了设计计算的效率. 因此国内外学者一直致力于研究如何克服传统有限元法的缺点.

近年来，在努力开发先进数值方法时，文献[9]将无网格中的应变光滑技术与传统有限元法相结合，引入梯度光滑的操作概念，提出一系列广义梯度光滑有限元法. 其包括用梯度光滑技术分别对构造的节点光滑域、边光滑域以及面光滑域进行光滑操作而形成的点光滑有限元法(NS-FEM)[10]、边光滑有限元法(ES-FEM)[11]以及面光滑有限元法(FS-FEM)[12]. 3种方法各有优缺点. 相对于传统有限元法，NS-FEM在精度和效率方面有所提高. 但是NS-FEM在空间上是稳定的在时间上可能是不稳定的，并且由于“过软”特性而不能直接应用于解决动态问题[13]. 然而，ES-FEM可以克服时间不稳定性[14]，由于本文研究的是时变涡流场，因此克服时间不稳定性对于时变涡流场分析尤其重要. 此外，对于固体力学问题，具有线性积分的ES-FEM比线性有限元法更加准确和有效[15]. 至此，ES-FEM近年来得到了广泛的应用. 对于FS-FEM更适用于三维问题.

本文提出一种用ES-FEM与边界元耦合法计算二维瞬态涡流场. 该耦合法同时具有ES-FEM计算精度高以及边界元法占用计算机内存少等优点. 首先将问题域离散化为一组三角形单元，然后进一步构造与三角形单元边相关的积分域，采用伽辽金加权余量法，推导出基于边光滑有限元-边界元耦合算法的离散公式，在导体区域内采用ES-FEM，非导体区域内采用边界元法. 研究导体区域的磁场分布，并与测量结果和有限元-边界元耦合法计算结果进行对比. 计算结果表明，在相同网格密度条件下，基于ES-FEM边界元耦合法计算精度更高，该方法具有更好的应用前景.

1 电磁场的分析模型

电磁分析的问题实际上是在给定边界条件下求解一组麦克斯韦方程组的问题. 如图1所示，为开域涡流场求解区域示意图. 整个电磁场求解域分为涡流区V1和非涡流区V2，Γ1是V1和V2的内部边界，非涡流区V2包括无源电流的非涡流区和有源电流的非涡流区.V1区域内采用ES-FEM，V2区域内采用BEM, 在内部边界上满足的边界条件为

(1)

(2)

ν

(3)

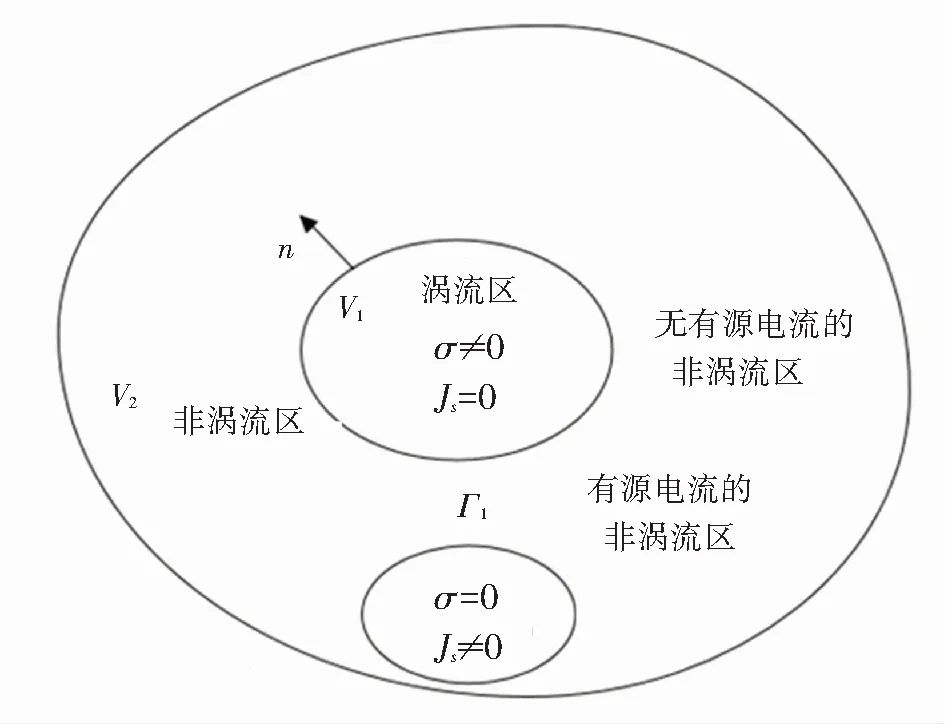
图1 开域涡流场求解示意图

2 边光滑有限元-边界元耦合法介绍

2.1 边光滑有限元法

边光滑有限元法是在求解有限元的基础上对其求解域进一步光滑，形成多个光滑子单元，然后在新形成的光滑子单元内引入梯度光滑操作，梯度光滑操作是指在新形成的光滑域上对有限元求解的系数矩阵进行光滑平均运算，其数学表达式为

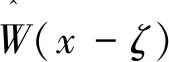
其中Ax为光滑域的面积. 图2为边光滑有限元法的计算流程图.

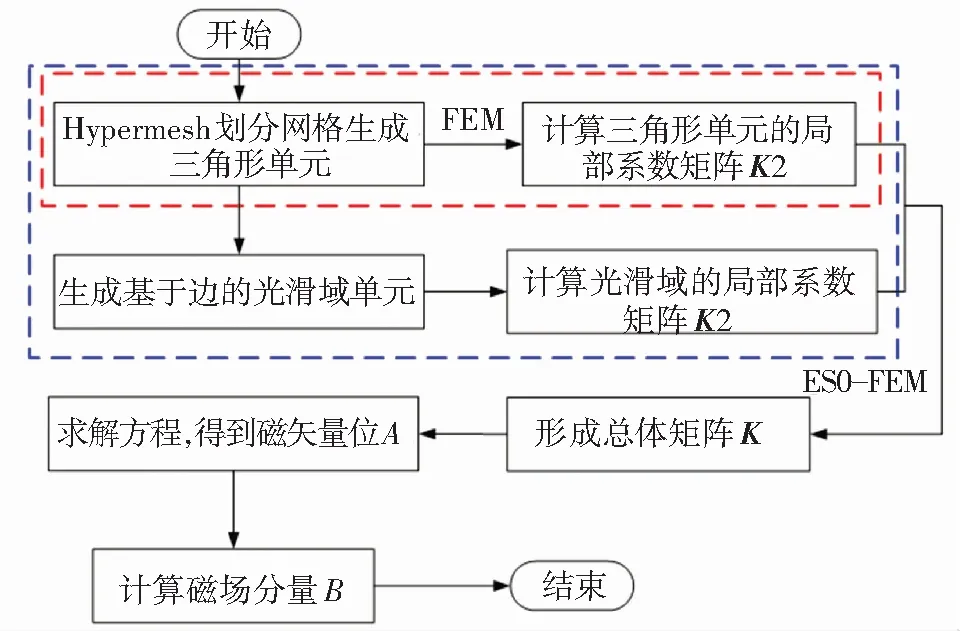
图2 计算流程图

对于二维求解域，先用划分软件Hypermesh对其进行三角形划分，其中生成N个节点和p条边. 传统有限元的离散矩阵[16]为

(4)

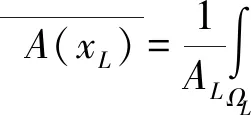
(5)

式中AL为光滑域的面积，在二维求解域单元内，AL的表达式可根据参考文献[9]计算得到.

图3 基于边的光滑域

对式(7)进行格林公式换算，那么对光滑域内位函数的面积分可以转化为光滑域边界上的线积分，即

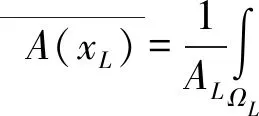
(6)

将式(6)代入式(5)中，可得

(7)

其中：

(8)

(9)

对光滑域ΩL采用高斯积分，式(12)的光滑域边界积分形式为

(10)

式中：NA为电磁场求解域边界L的个数，NB为高斯点的个数，δq为高斯点积分的权函数.

由式(10)可知，dij是由光滑域各个边中点处的形函数求得，而各个中点处的形函数可通过场节点插值得到，如图4所示，点1、2、3、4分别为场节点，A、B分别为中心节点，g1、g2、g3、g4分别为高斯积分点[17].

基于边L的光滑有限元系统的局部光滑域的系数矩阵可以写成：

(11)

对上述局部系数矩阵进行整体组装，得到域内整体系数矩阵为

(12)

图4 ES-FEM形函数分布

2.2 边界元法

对于非涡流区应用格林公式，可得对应边界积分方程[5]为

(13)

采用伽辽金余量法对式(13)离散，得

(14)

2.3 基于边光滑有限元边界元耦合算法

将式(4)和式(14)联立，可得

(15)

对式(15)中的导数项，采用向后差分，即

(16)

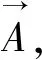
(17)

(18)

3 计算算例与分析

3.1 脉冲线圈-铝板表面磁场分布

脉冲线圈-铝板的结构参数：矩形截面为0.6 mm×4.8 mm的铜丝缠绕成内径、外径分别为3.2、25.5 mm,匝数为30的圆柱形线圈[19]. 脉冲线圈流过的瞬时电流波形，如图5所示. 在线圈正上方放置0.8 mm厚的铝板，电导率δ=3.48×107s/m. 线圈与铝板的间隙为2 mm. 采用本文所提的基于边有限元边界元耦合法求得铝板表面的磁感应强度，其结果分别与测量值以及有限元-边界元法的计算结果进行对比，如图6～8所示.

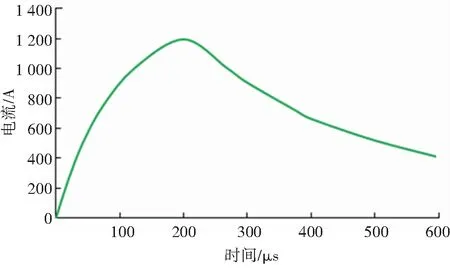
图5 脉冲电流随时间变化

图6 磁矢量位A线的分布云图

图7 切向磁感应强度随时间的变化(r=10 mm)

由图6可知，离线圈越近，磁矢量位A值越大，与实际情况一致，说明本文的计算方法合理. 为了验证本文所提方法的计算精度，设相对误差Bi为

(19)

式中：B0为测量值，B1是计算值，i=x、y分别代表磁场沿切向、垂直方向的磁场分量.

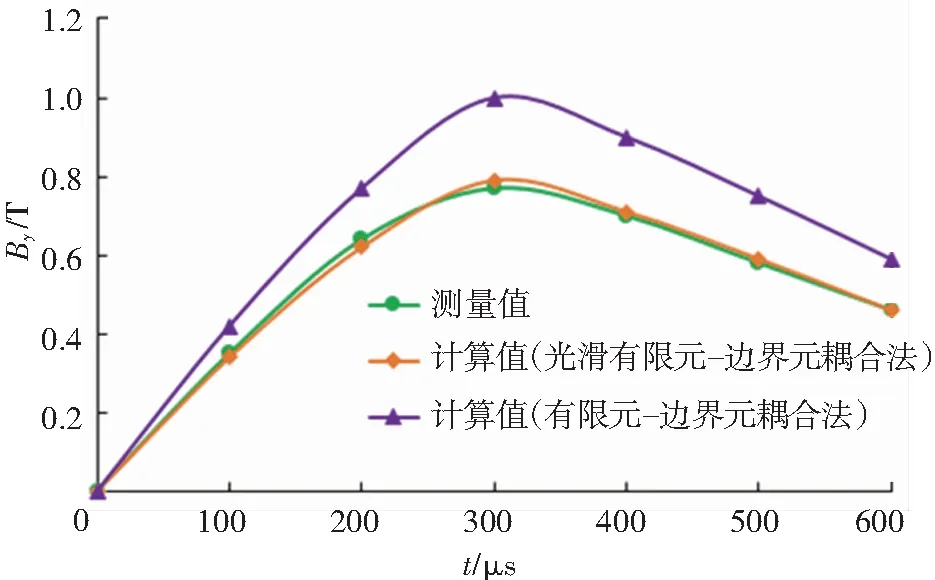
图8 垂直磁感应强度随时间的变化(r=7.6 mm)

由图7、8可知，基于边光滑有限元边界元耦合法与测量结果一致，因此可用本文所提的方法计算涡流场. 在网格单元划分密度相同的条件下，运行两种方法效率对比见表1，虽然本文所提方法的运行时间稍长于有限元边界元耦合法，但其计算精度远远高于有限元边界元耦合法，另外，对于目前计算机的计算能力而言，本文通过改变模型的大小，对比两种方法的运行时间. 由表2可知，两种方法运行时间的差别可以忽略. 由此可知，在计算涡流场时基于边光滑有限元边界元法能大大提高计算精度.

表1 效率对比

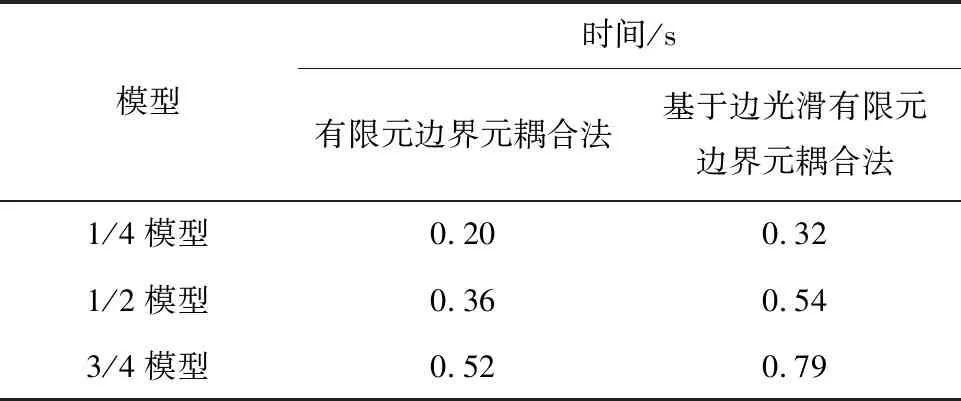
表2 运行时间对比

综上所述，在进行涡流场分析时，应优先考虑基于边光滑有限元边界元耦合法.

3.2 铝板表面磁场分布的影响因素

3.2.1 电流密度变化的影响

脉冲电流-铝板模型参数如上所述，在进行电流密度对其磁场影响分析时，保持模型的其他参数不变，改变流过脉冲线圈的电流密度Js从10×106A/m2到180×106A/m2变化，间隔为30×106A/m2. 则上述电流密度变化的情况下铝板表面磁场分量分布如图9所示.

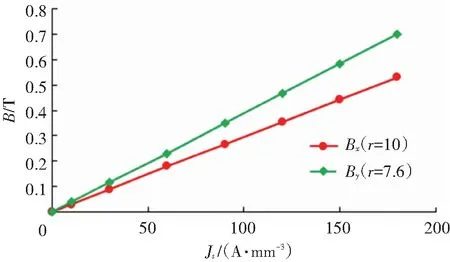
图9 磁场强度随涡流密度的变化

如图9所示，磁场强度随涡流密度的增大而增大，这是因为涡流密度Js与系数矩阵F成正相关，即当Js增大时，F增大. 由式(20)可知,随着F增大，所求磁矢量位A增大，因此磁场强度增大.

3.2.2 脉冲线圈-铝板间隙变化的影响

脉冲电流-铝板模型参数如上所述，在进行脉冲线圈-铝板间隙对其磁场影响分析时，保持模型的其他参数不变，改变间隙h从2 mm到8 mm之间变化，间隔为1 mm. 则上述间隙变化的情况下铝板表面磁场分量分布如图10所示.

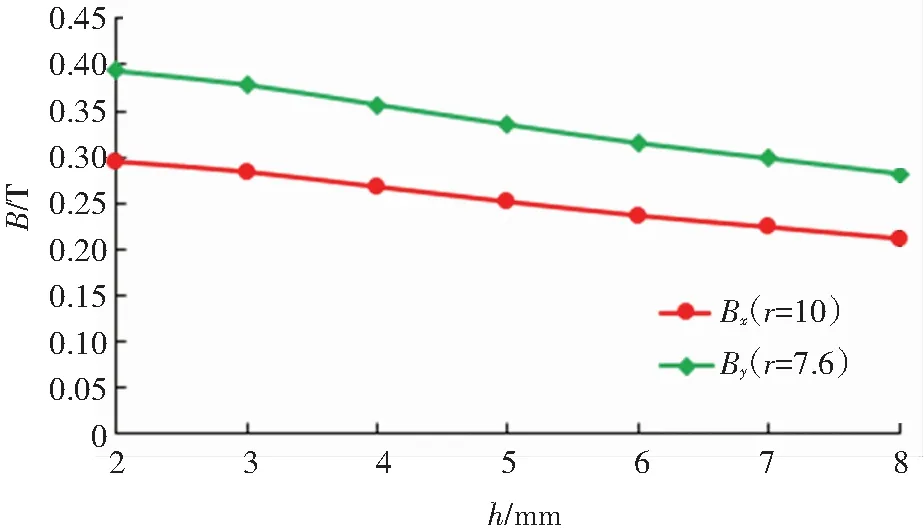
图10 磁场强度随间隙的变化

由图10可知，随着脉冲线圈与铝板之间间隙h的增大，磁场强度逐渐减小. 这说明如果为了增大铝板中的涡流作用，即产生大的脉冲力，那么脉冲线圈需尽可能近的接近铝板.

4 结 论

1)提出了一种计算涡流场分布的基于边光滑有限元边界元耦合法，该方法即具有ES-FEM计算精度高和边界元法占用内存少的优点，并详细给出了该方法的推导过程. 同时，利用本文所提的基于边光滑有限元边界元耦合法计算分析脉冲线圈上方铝板表面的磁场分布，与测量结果对比表明，该方法是正确合理的.

2)在单元网格密度划分相同的条件下，将本文得到的计算结果与传统有限元边界元耦合法计算得到的结果对比，虽然本文所提方法的运行时间稍长于有限元边界元耦合法，但其计算精度远远高于有限元边界元耦合法，另外，对于目前计算机的计算能力而言，两种方法运行时间的差别可以忽略.

3)在计算模型的其他参数保持不变，只改变涡流密度的情况下，磁场强度随涡流密度的增大而增大且曲线增大率几乎保持不变，同理，磁感应强度随着脉冲线圈与铝板之间间隙h的增大而减小，且其曲线降低率也几乎保持不变.