一种光电稳定平台摩擦力新型补偿方法

2021-03-17

中南大学学报（自然科学版） 2021年2期

(中国科学院西安光学精密机械研究所，陕西西安，710100)

光电平台隔离飞行器扰动稳定视轴(line of sight,LOS)的能力直接决定了可见光、红外载荷成图的清晰度以及激光照射的稳定程度。两轴两框架航空光电平台的方位框为外框，内俯仰框搭载光学载荷及惯性传感器，在工作过程中，飞行器姿态变化及振动等扰动，经过摩擦力矩、线绕力矩等耦合到光电平台，造成视轴运动，在这些耦合中，摩擦力的影响最为突出[1]，由于摩擦的非线性特性以及在低速换向时复杂的死区特性，经典控制的方法抑制能力有限，因此为了进一步提升系统的稳定精度，需要研究新的摩擦补偿方法。

近年来，学者们提出了多种光电平台摩擦力补偿策略，可总结为2类方法：一类为采用自抗扰控制的方法，它将包含摩擦力的扰动作为总和扰动一部分，经扩张状态观测器观测后进行补偿。文献[2−4]基于非线性自抗扰控制方法补偿摩擦力，文献[5−7]引入基于线性自抗扰的控制方法，这些方法均取得了一定的效果。但是，基于非线性的自抗扰控制其调节参数多、运算量大、计算复杂、调试需花费时间较长[8]；虽然线性自抗扰控制方法调试参数少、整定简单、抗扰能力与扰动幅值无关[9−10]且在低中频段具有较好的频域特性，但是其高频段抗扰性能差，观测器的相位滞后限制其对实际摩擦特性高频扰动的估计能力。另一类方法为基于摩擦模型的补偿方法，该方法将补偿量直接叠加于系统控制量，抵消摩擦力矩，其本质上是一种前馈补偿方案，补偿响应快[11]。工程中常见的摩擦模型有静态摩擦模型和动态摩擦模型。文献[1,12]引入动态的LuGre模型，补偿摩擦力，取得了补偿效果，但是该方法建模较复杂，建模过程需要高精度的传感器，需要拟合的参数多。

工程中应用较多的为静态Karnopp[13]和Stribeck模型，Stribeck 模型零速率检测实现复杂，Karnopp模型通过设立零速率区间处理零速率检测问题，该区间决定补偿的精度，零速区间越小，低速部分的摩擦补偿效果越好。但是，在光电稳定平台系统中，零速区间的设置受到测速精度的影响。传统的方法采用编码器差分测速，由于编码器精度的限制，速度分辨率较差，导致零速区间设置较大，低速时补偿效果受限。

本文作者借鉴所述各方法的优势及特点，从易于工程实现的角度出发，提出一种新型补偿方法，通过对速度稳定环抑制摩擦力的过程分析，提出在低速时采用陀螺与编码器融合估计速度的方法改进Karnopp摩擦模型；为了解决补偿模型建模误差以及实际工作中系统摩擦特性随环境等因素发生漂移变化造成该补偿效果下降的问题，在此基础上引入线性扩张状态观测器(linear extended state observer,LESO)，观测并补偿实际模型与补偿模型的差异带来的误差。利用摩擦模型的前馈补偿特点，快速响应过零换向阶段的高频非线性特性，利用LESO的中低频特性，补偿摩擦特性漂移变化，提升系统鲁棒性。

1 经典速度稳定环摩擦力抑制特性

本文所研究的航空光电平台为力矩电机直接驱动的两轴两框架平台，搭载在飞行器上，实现对指定目标的稳定指向，工作中飞行器姿态及振动等的影响引起光电平台基座运动。在工作过程中，光电系统基座的扰动耦合至光电平台方位框、俯仰框，引起框架定、转子产生相对运动或相对运动趋势，产生摩擦力矩，在该力矩的作用下，光学载荷开始运动，产生视轴运动，被安装于内框架的两轴陀螺感知后，在经典稳定环控制作用下，该运动被驱动电机向相反方向运动抵消。考虑到摩擦耦合在方位与俯仰轴的过程相似，本文以俯仰轴为例对摩擦补偿方法进行研究。

本系统选配含有电流环的驱动器，电流环采用硬件电路实现，通过合理的配置电流环参数，使电流环带宽达到1 kHz以上，因电流环带宽较速度环带宽大得多，将电机定、转子相对运动产生的反电动势波动影响消除在电流环内[14−16]。经过电流环简化后，速度稳定环模型如图1所示。图中：J为折合到电机轴上的俯仰框架转动惯量；1/s为积分算子；Tm为电机输出力矩；ωo为俯仰框架输出相对惯性空间速度；ωb为基座扰动；ωr为框架定转子相对运动；f(∙)表示摩擦耦合算子；Tf为耦合的摩擦力矩；Cm为力矩电机的力矩系数；Gc(s)表示稳定环经典PI控制器；Kg为速度反馈环节增益。

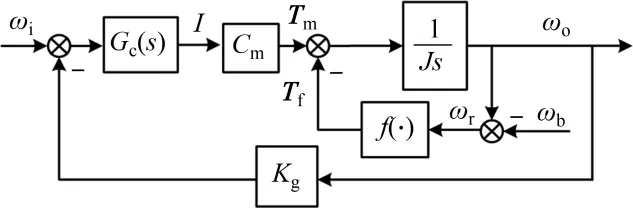
图1 速度稳定环结构图Fig.1 Mathematical model of velocity-stabilizedloop

为了分析摩擦力耦合及抑制过程，对速度稳定环进行仿真，稳定环输入指令为0，在基座上按照幅值为1°，频率为2 Hz 进行扰动，在经典控制作用下，俯仰方向扰动与视轴运动情况仿真波形如图2所示。

由图2可知：经典速度稳定环摩擦力的抑制效果与定、转子相对运动速度ωr有关，相对速度ωr在0附近，抑制效果差。由基座扰动速度波形可以看出，相对速度在0附近时，刚好发生基座扰动换向过程，此时摩擦力方向突变，经典线性控制器受系统噪声及能量的限制，Kp和Ki取值不可能无限大，因此系统带宽有限，导致经典控制产生的力矩Tm如式(1)所示，无法快速跟踪逼近摩擦力Tf的突变进行补偿，造成在零速附近稳定效果较差。

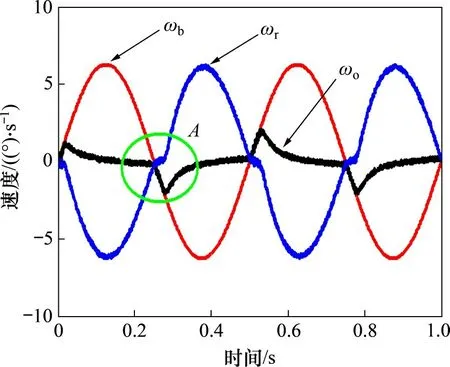
图2 视轴运动与基座扰动运动仿真图Fig.2 Simulation diagram of LOS motion and base disturbancemotion

2 基于传统Karnopp模型补偿方法

相对运动或运动趋势是产生摩擦力矩的原因，若可以测量出此相对运动，则可将此相对运动产生的摩擦力矩前馈给控制系统，前馈的响应速度快，因此在经典PI 稳定控制器基础上利用摩擦模型前馈的方法可以进一步补偿摩擦力。易于工程应用的传统Karnopp模型为

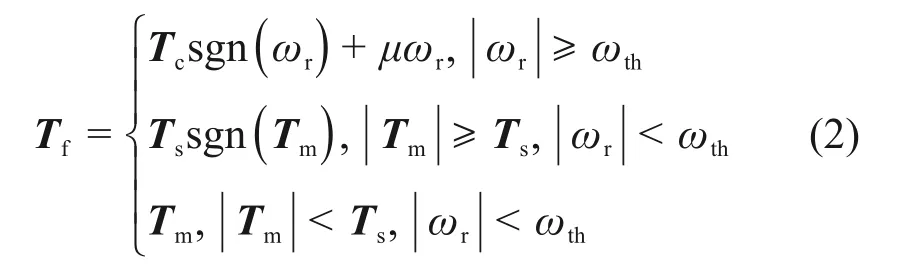
式中：ωr为定转子相对速度；ωth为一个很小的正常数，形成一个零速区间，在该区间内的速度强制为0；Ts为最大静摩擦力矩；Tc为库仑摩擦力矩；μ为黏滞摩擦因数。显然，零速区间越小，模型描述越准确，补偿效果越好，传统测量相对速度的方法为采用旋转变压器或编码器等测角传感器差分得到，当相对速度较大时，该方法测量精度高，但是因这些测角传感器的位宽有限，差分后速度分辨率很低，导致低速时测速精度差。

本系统中所用编码器为Netzer 的DS−58 型，如图3所示，该编码器分辨率为18 bit，本系统速度稳定环控制周期为1 ms，由此可知差分后的速度分辨率Δωr为1.37(°)·s−1。

分辨率测试波形如图4所示。零速区间选取需大于测速分辨率，因此，用该方法测速时，在速度分辨率为1.37(°)·s−1内的相对速度无法感知，该速度区间内产生的扰动无法通过前馈补偿，只能靠经典控制进行补偿。若通过增大差分时间提高角速度分辨率，滞后时间会增大，影响补偿的动态性能。

图3 编码器外形Fig.3 Encoderprofile

图4 编码器差分速度分辨率测试Fig.4 Encoder differential speed resolution test

3 新型补偿方法

3.1 改进型低速估计方法

光电稳定平台为动基座平台，考虑其与定基座转台的区别，当俯仰框架定转子相对速度在编码器速度分辨率内时，其相对运动速度较小，可近似认为定转子无相对运动，此时摩擦力主要表现为静摩擦力，在静摩擦力的作用下，定子带动转子以相同速度共同运动，如图5所示。

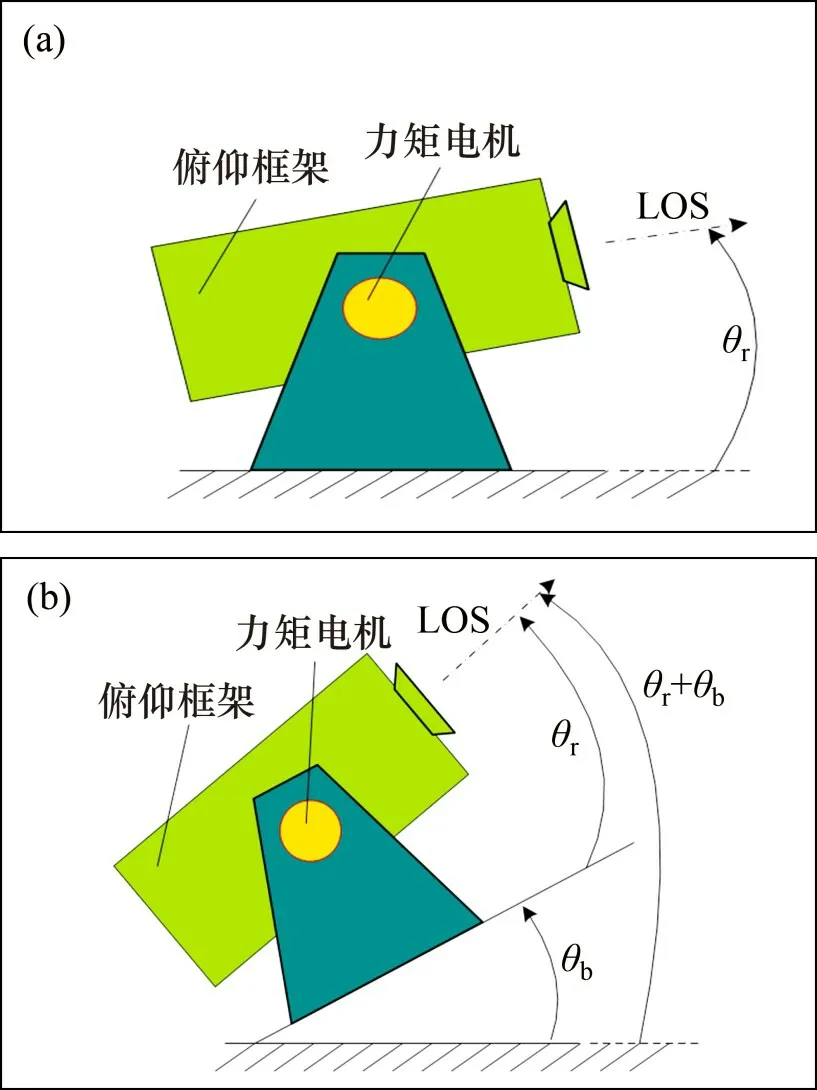
图5 定转子相对速度较小时视轴运动情况Fig.5 LOS motion of optic axis when relative speeds of stator and rotor are small

由图5可以看出，视轴位置由a到b，框架定转子之间的相对位置θr未发生变化，基座的运动带动框架共同运动θb，使得视轴位置由θr变为θr+θb，这与图2中A位置波形也相吻合，在相对运动ωr接近0 附近时，俯仰框运动ωo与基座运动ωb波形相重合。

因此，在编码器速度分辨率区间内，相对运动可以利用陀螺数据来估计基座的运动，因期望的光轴稳定速度为0，由此可以求得两者相对运动速度估计值，以此作为编码器零速区间内的相对速度，其估计方法为

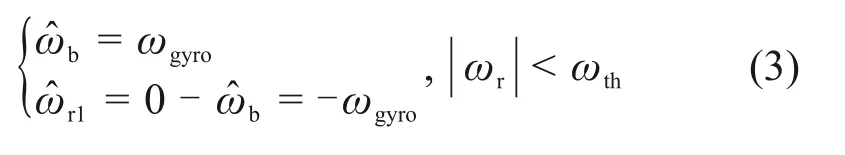
其中：ωgyro为陀螺速度。

显然，光电系统中陀螺的速度分辨率比编码器测速的分辨率高很多，本系统中使用的STIM210 型陀螺，分辨率达到0.01(°)·s−1，陀螺分辨率测试曲线如图6所示，根据陀螺噪声带，新的零速区间可取为0.1(°)·s−1。这样，在编码器速度分辨率内，用光电系统现有陀螺估计相对运动可进一步缩小零速区间，提高零速度附近摩擦模型描述的准确性，改善零速度附近的补偿能力。

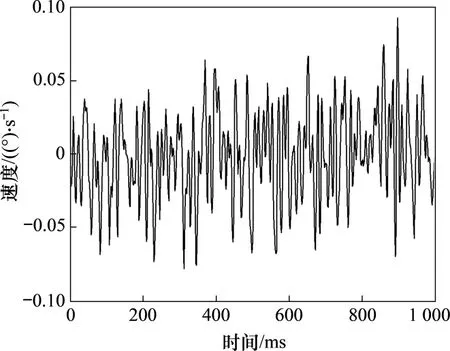
图6 陀螺速度分辨率测试结果Fig.6 STIM210 gyro speed resolution test results

由此可得到改进型Karnopp 模型如式(4)和式(5)所示：

当|ωr|≥ωth时：

当|ωr|<ωth时：

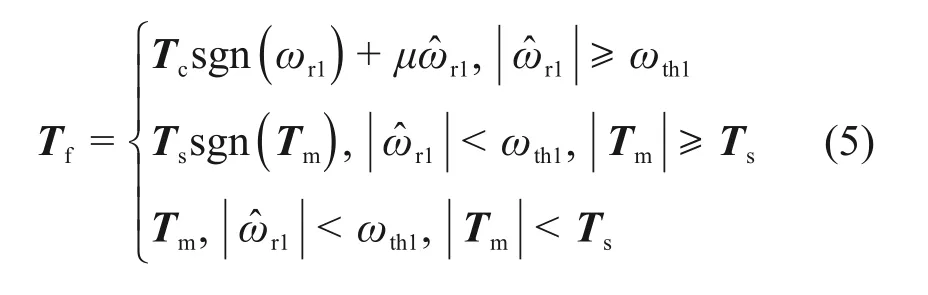
其中：ωth为由编码器确定的零速区间；ωth1为由陀螺决定的零速区间；ωr为定转子相对速度；为ωth区间内估计的相对速度，取值为-ωgyro。

3.2 改进型Karnopp摩擦模型的辨识

首先，辨识静摩擦力。将光电平台基座固定，方位框处于锁紧状态，俯仰框速度环开环状态，缓慢增加驱动器电流，同时，采集驱动器输出电流和转速信号，因基座静止，因此以陀螺反馈测得相对速度，当速度信号发生明显变化时，记录对应的电流数据，即为最大静摩擦力等效电流。

其次，辨识库仑及黏滞摩擦力。系统处于速度闭环，设定系统以不同的恒定速度运行，平台速度与对应电流关系如图7所示。

对图7进行拟合并辨识参数，得改进型模型如式(6)和(7)所示。本系统改进型模型中编码器零速区间ωth和ωth1分别1.6(°)·s−1和0.1(°)·s−1。

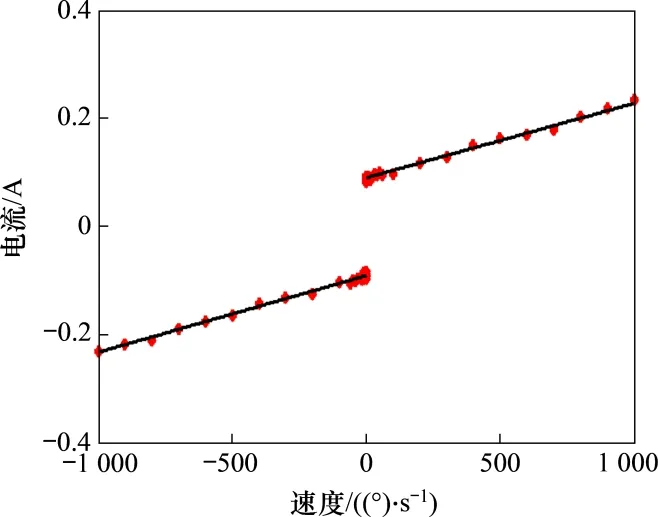
图7 速度与对应驱动电流关系Fig.7 Velocity and corresponding driving current

当|ωr|≥1.6(°)·s−1时，

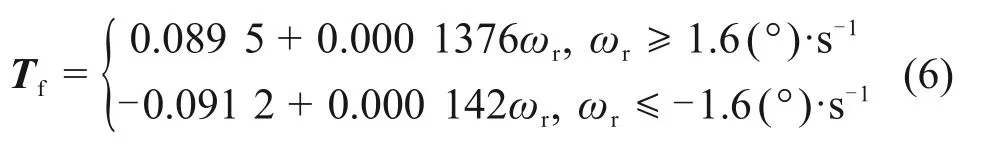
当|ωr|<1.6(°)·s−1时，

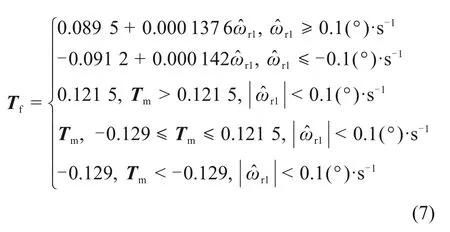
3.3 扩张状态观测器的引入

摩擦力扰动首先表现为相对运动，由编码器或陀螺融合观测相对速度，经上述改进型模型后前馈补偿给系统，响应速度快，可以补偿摩擦特性的高阶非线性特性。但是因补偿模型存在建模误差，系统随着工作温度气压等工况变化，实际摩擦特性与补偿模型产生差异，因此在改进型Kanopp模型基础上，本文引入扩张状态观测器[17−18]构成新型补偿方法，利用改进型Kanopp 模型提升零速附近的补偿能力，利用扩张观测器观测并补偿因模型差异造成的误差，提高模型补偿的鲁棒性。基于摩擦模型的新型摩擦力补偿结构如图8所示。

引入改进型摩擦补偿模型后，因大部分摩擦力已经被模型补偿，光电平台模型变为

图8 基于摩擦模型的新型摩擦力补偿结构Fig.8 Principle diagram of new friction compensation method based on friction mode

其中：ΔTf为补偿模型误差残余的摩擦力矩及其他扰动力矩(线绕力矩等)，取状态变量将ΔTf扩张后的状态方程如下：

将ΔTf作为新的状态进行观测，以光电平台电流I和转速ωo为输入，输出为ΔTf观测值，建立扩张状态观测器：

4 实验验证

为了验证上述方法的效果，将光电系统安装于地面三轴摇摆台上，模拟飞行器扰动，验证稳定效果。对引入上述改进型Karnopp 模型和LESO构成新型补偿方法进行了速度稳定度实验和稳定精度测试实验。

速度稳定环指令为0，系统工作于稳定模式，控制周期为1 ms，施加幅值为1°，频率为2 Hz 的典型扰动，采集记录光电系统中陀螺反馈数据，分别测试各补偿方法的稳定效果。图9所示为采用经典PI 控制、PI+传统Karnopp 模型与PI+改进Karnopp 模型补偿效果对比，图10所示为经典PI、PI+改进Karnopp 模型与PI+改进Karnopp 模型+LESO补偿效果对比。

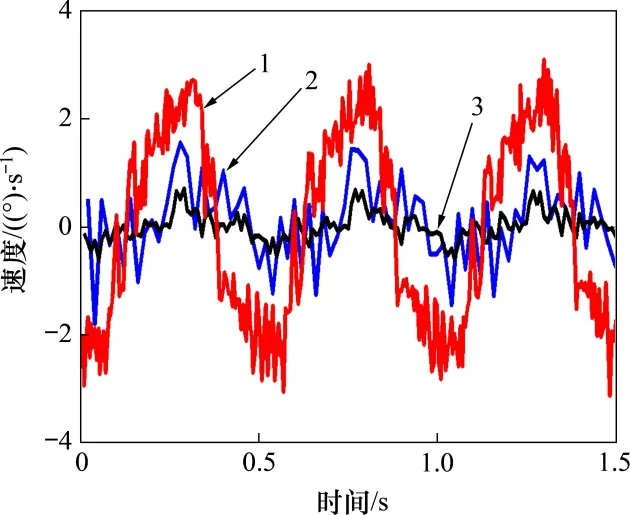
图9 不同Karmopp补偿模型速度稳定波形Fig.9 Velocity response to disturbance with Karnopp and improved Karnopp compensation methods

图10 引入LESO速度的Karmopp补偿模型的速度稳定波形Fig.10 Velocity response to disturbance with improved Karnopp and LESO

由图9可知：在幅值为1°，频率为2 Hz 的扰动下，经典PI 控制方法抑制能力有限，最大波动速度达到2.6(°)·s−1。引入传统Karnopp 模型后，反应在编码器零速区间外的摩擦扰动由补偿模型前馈作用迅速补偿，速度波动减小到1.5(°)·s−1内，稳定效果得到一定的改善，但是受限于编码器差分测速的精度，编码器零速区间内补偿效果较差。引入改进型Karnopp模型后，速度波动进一步减小到0.6(°)·s−1，且波动的时间减小，仅在换向时刻有小幅度波动，表明改进型模型的低速观测方法在传统模型零速区间内起到了补偿作用，使得在换向处速度波动幅值及时间有明显改善。由图10可知：在改进型模型基础上引入LESO后构成新的补偿方法，速度稳定度达到0.5(°)·s−1，这是因为LESO 的引入补偿模型误差及线绕力矩等其他扰动。

为了验证引入新型补偿方法的鲁棒性，人为改变系统补偿模型参数10%，将补偿模型式(6)和式(7)中Tc，μ和Ts参数均增大10%，以此模拟系统模型的变化造成补偿模型与系统模型的差异，在上述条件下，分别进行摇摆实验，验证参数变化时引入和未引入LESO 的速度稳定效果如图11所示。

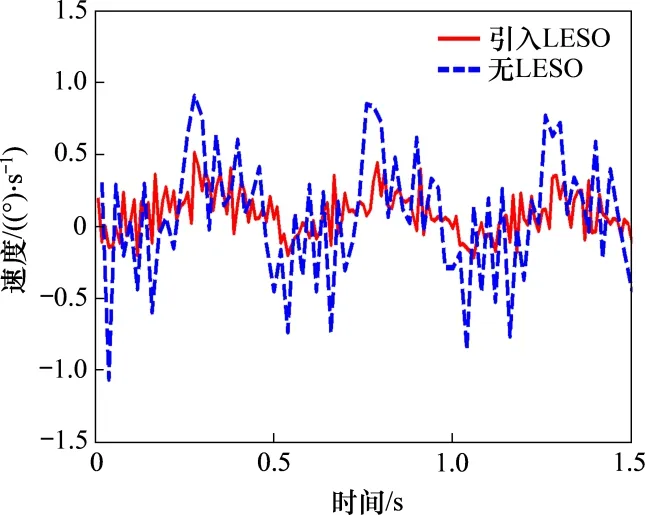
图11 模型参数变化10%时LESO引入效果对比Fig.11 New compensation method with and without LESO when model parameters change in 10%

由图11可知：补偿模型的参数改变10%后，未引入LESO 时补偿效果下降，速度稳定度由0.5(°)·s−1增大到0.9(°)·s−1，新补偿方法下，换向时刻的速度波动维持在0.5(°)·s−1左右，保持较好的隔离效果。

同时对比测试了上述各补偿方法的视轴稳定精度，将光电系统中搭载的可见光相机拉至最长焦即小视场，焦距129 mm，像元大小4.2 μm，在上述扰动下，观测光管十字靶，逐帧存储视频序列，判读每帧图像靶标十字中心的位置坐标变化，测试稳定精度。分别采用经典PI、PI+传统模型补偿、PI+新型补偿以及在补偿模型参数人为改变情况下引入与未引入LESO试验，逐帧分析视频序列十字靶中心的晃动量如表1所示。

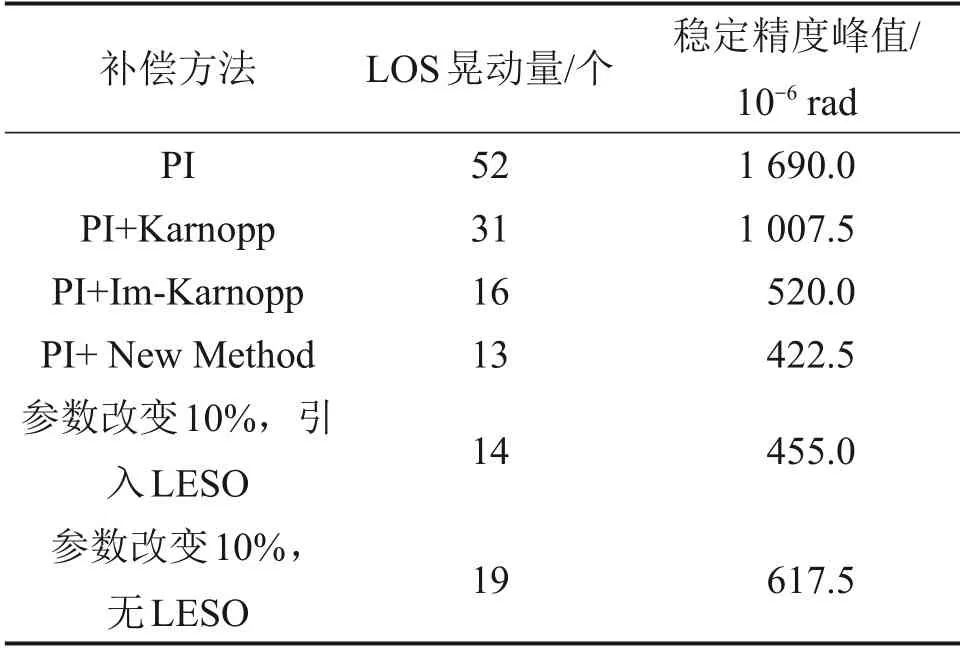
表1 不同补偿方法视轴晃动量Table 1 LOS jitter with different compensation schemes

由表1可知：采用经典控制时，稳定精度峰值为1 690.0×10−6rad，引入传统Karnopp 模型后，稳定精度峰值为1 007.5×10−6rad；引入改进型模型后，稳定精度峰值为520.0×10−6rad，采用本文的新型补偿方法后，稳定精度峰值减小到422.5×10−6rad，与传统模型相比，隔离度提升了58%；当人为改变系统补偿模型参数10%时，未引入LESO 的视轴稳定精度峰值增加到617.5×10−6rad，新方法的稳定精度峰值为455.0×10−6rad，与模型匹配时隔离效果相当。表明在改进型模型基础上引入LESO仍具有优异的扰动隔离性能，表现出较强鲁棒性。