基于改进遗传算法的球团矿图像分割

李 超，刘 琼

（武汉科技大学 信息科学与工程学院，湖北 武汉 430080）

0 引 言

随着钢铁行业的发展，冶炼所需的矿石缺口将会越来越大，而我国铁矿石储量中绝大部分为含有大量有害杂质的贫矿，需要研磨精选才能进行冶炼。因此人造块入炉率自20 世纪70 年代起呈上升趋势，而人造块的两个主要方法，即烧结法和球团法工艺优化的重要性也在不断提升。相比烧结法，球团法生产的球团矿具有品位高、强度高、易还原、粒度分布均匀、透气性好等特点，对于提高高炉利用效率有重要价值[1]。粒径分布是球团矿重要的几个质量指标之一，传统球团矿粒径检测方法主要是筛分法，它存在耗时长、取样数量少、误差偏大等缺点，无法及时、准确地获取球团矿粒径分布来调整生产工艺，以达到提高生产效率的目的。而通过图像处理技术采用计算机实时获取球团矿粒径有着效率高的特点，且具有一定的实用价值。粒径检测系统中最为重要的部分就是图像分割部分，分割结果直接影响着球团矿粒径检测的准确率。而使用相机对球团图像采样时，由于现场环境复杂，往往存在一部分球团出现黏连现象造成分割效果不理想。

现有文献关于目标图像的分割方法主要包括阈值分割法、分水岭分割法和边缘检测分割法等。阈值分割法有着效果明显、易于实现的优点。文献[2]采用最大类间方差法分割矿石图像，然后使用开闭操作去除图像中多余噪声。文献[3⁃4]采用遗传算法和改进遗传算法结合阈值法分割目标图像，但是阈值分割法分割效果依赖于阈值的选择，阈值的选择不当会造成黏连物体分割不佳。分水岭分割法在分割黏连物体边缘时有着较好效果，文献[5]采用形态学top⁃hat 操作和分水岭分割结合方法来分割球团矿图像，文献[6]采用标记与分水岭算法结合的方法分割矿物图像。虽然分水岭算法分割黏连图像效果较好，但是极易受图像中噪声干扰，若是直接对图像使用分水岭分割会产生过分割现象。边缘检测分割法具有定位准确，运行速度快的优点。文献[7⁃8]利用小波变换法提取目标图像边缘。文献[9]采用多种边缘检测算子相结合以获取黏连的玉米粒边缘。在面对边缘不明显，表面粗糙的球团矿图像时，由于边缘检测算子分割方法的抗噪声能力弱会导致分割效果并不是很好。

以上单一的方法在面对表面粗糙不平，边缘黏连严重的球团矿图像时，均存在一定的未分割或过分割问题。针对以上问题，本文提出了一种基于改进遗传算法阈值分割法和标记分水岭算法结合的分割算法，有效改善阈值分割方法耗时长且黏连球团边缘分割效果不佳和直接应用分水岭分割产生的过分割问题。

1 图像阈值分割

1.1 图像预处理

由于采集到的球团矿为彩图，信息量较大，且存在很多噪声点，所以在图像分割之前需要对球团矿图像进行一定的预处理操作以达到更好的分割效果。首先对图像进行灰度化操作，然后采用自适应直方图均衡化来调整图像对比度获得更多细节，最后使用7×7 模板的中值滤波达到去除噪声并保护边缘的目的。球团矿原图以及预处理各阶段的效果如图1 所示。

1.2 改进遗传算法的最大类间方差法分割

最大类间方差法通过遍历图像中所有灰度值，计算所有灰度值类间方差，并找出其中使背景和目标差别最大的灰度值以作为最佳分割阈值。该分割方法处理球团矿图像后，图像信息得到最大程度保留，边缘较为清晰，中间区域分割理想，但是存在一部分黏连球团分割效果不佳，且单一阈值法分割耗时偏久。所以本文引入改进遗传算法与最大类间方差法结合以达到加快获得最佳分割阈值的效果并且减少了传统遗传算法存在的不稳定性问题。

遗传算法是模拟生物进化过程的计算模型，对种群进行反复的遗传、交叉、变异操作。运用目标适应度函数对个体进行评价，通过优胜劣汰机制以获得最优解或者满意解。

图1 球团矿原图及预处理各阶段效果

通过遗传算法与最大类间方差分割法结合，可以更快地获得分割图像的最佳阈值，然而传统遗传算法存在收敛性差和容易陷入局部最优解问题，容易导致分割结果不佳。为避免此问题，对传统的遗传因子和评价函数进行了改进。遗传算法结合最大类间方差法分割过程如图2 所示。

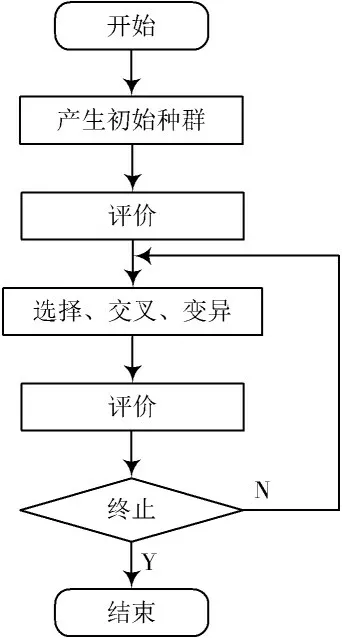
图2 遗传算法流程

基于改进遗传算法的分割算法流程如下：

1）编码和初始种群

由于所处理的图像为灰度化之后的图像，灰度级数为256 级，所以采用8 位二进制数来代表分割的最佳阈值，初始种群数目设为20。

2）选择适应度函数

根据最大类间方差法法分割原理，设置要处理的图像灰度级数为L，像素点总数为N，灰度级数为i的像素点个数为ni，则i的个数占总体的比例为：

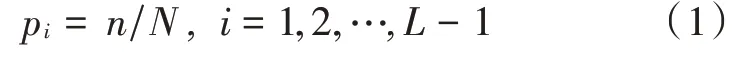
图像中所有灰度出现概率为1，即：

假定分割的最佳阈值为t，将图像分为目标区域C0（0，t）和背景区域C1（t，L-1）两部分，则该图像的灰度均值为：

目标区域灰度均值为：

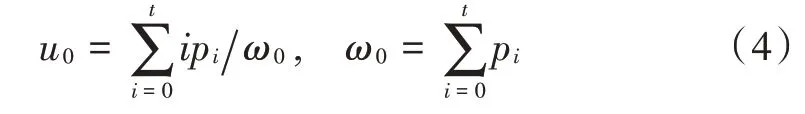
背景区域灰度均值为：

所以有：

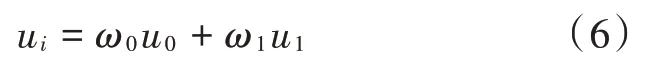
因此，类间方差为：

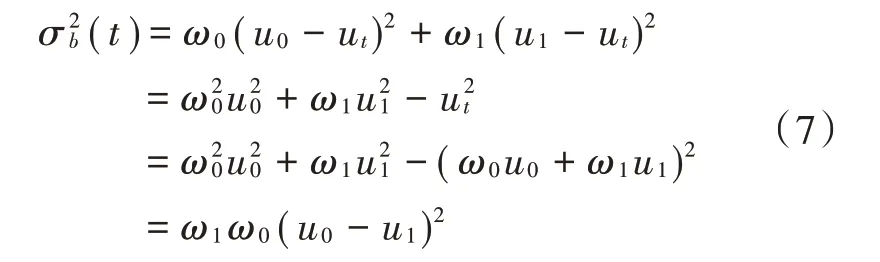
分割的最佳阈值t即为使(t)最大的阈值，采用式（7）作为适应度函数[10⁃11]。

针对遗传算子操作改进如下：

1）改进其中选择算子

传统遗传算法若是变异产生了一个新的更优解，由于种群数量不足，在直接经过遗传操作后这个新变异出来的较优解将会被覆盖掉。通过强制将上一代的最大值进行保留，来保证种群不会产生退化。

2）改变种群操作中的交叉概率

传统遗传算法交叉概率Pc为一个固定值（0.4～0.9），固定交叉概率会导致分割阈值与实际最佳阈值不同，对分割效果会有不利影响。本研究中将原先固定交叉概率变为随迭代次数变化而变化的两个概率，在迭代早期提高交叉概率，避免随迭代淘汰太多个体陷入局部最优解。而在迭代后期，加快收敛速度，提高分割效率将适当降低交叉概率：

式中gen 为迭代次数。

3）改变遗传操作中的变异算子

由固定变异概率Pm改为随迭代次数变化而变化的变异概率Pm：

终止原则：反复执行评价、选择、交叉、变异操作直至满足最大迭代次数100，并且前后最佳阈值均指向同一阈值时此阈值为最优解。

2 标记分水岭分割及球团粒径分布

2.1 标记分水岭二次分割

由于经过改进遗传算法最大类间方差法分割后的图像对于图中部分黏连球团的边缘分割效果还是不太理想，所以需要对阈值分割后的图像使用标记分水岭[12]方法进行二次分割，以达到更好的分割效果。

在对图像进行二次分割之前，首先要采用边缘检测算子对获得的二值图像进行边缘增强。为了在一幅图像f的（x，y）位置处寻找边缘的强度和方向，选择的工具是梯度，梯度指出了f在（x，y）处最大变化率的方向。Sobel 算子[13]是一阶边缘增强算子之一，能够很好地抑制噪声干扰，它分别利用水平和竖直两个方向求导以获得梯度的近似值。

水平变化：将图像f与一个奇数的内核Gx进行卷积。例如当内核大小为3 时：

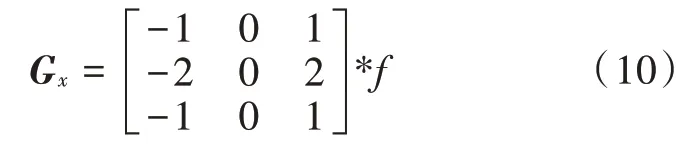
垂直变化：将图像f与一个奇数的内核Gy进行卷积。例如当内核大小为3 时：

在图像f中的所有像素上，结合以上两个结果求出梯度近似值G：

将经过边缘增强的二值图像使用标记的分水岭分割方法进行再次分割，可以对黏连球团及图片边缘部分更好的分割。然后采用形态学操作（腐蚀和膨胀）去除，使图像边缘变得光滑。本文总体分割流程如图3所示。

2.2 球团矿粒径分布统计

球团矿图像经过两次分割后，为统计球团矿实际粒径分布，采用hough 圆拟合来统计图像中球团矿个数和粒径分布。根据国标规定将球团矿粒径划分为3 个粒级，分别为0～8 mm、8～16 mm 和大于16 mm 三个粒级。将8 mm 球团矿和16 mm 球团矿置于相同拍摄条件下，8 mm 球团矿在图像中的直径平均像素为42 px，16 mm球团矿粒径平均像素为73 px。所以可以得出，图像中粒径像素在0～42 px 对应的球团矿粒径为0～8 mm，42～73 px 对应的是8～16 mm 粒径的球团矿，大于73 px 的则为粒径大于16 mm 的球团矿。

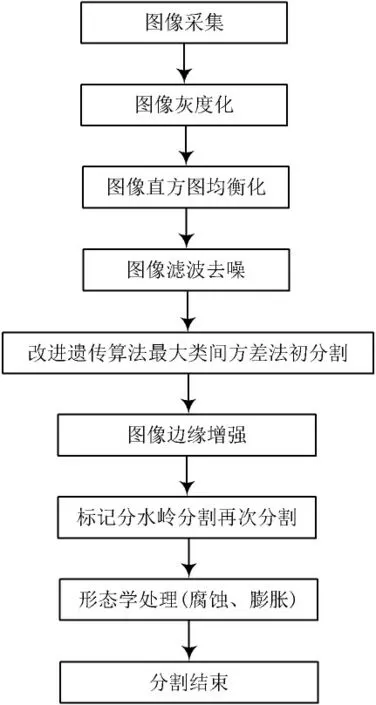
图3 分割算法总体流程

3 实 验

本文所有实验运行环境为Windows 10操作系统下的Matlab R2016a，处理器为英特尔Core i5⁃7400@3.00 GHz，内存为8.0 GB。对采集到的球团矿图像分别使用标记分水岭分割、改进遗传算法结合最大熵阈值法和本文算法进行分割，分割结果如图4 所示。通过比较几种算法分割的结果以评估本文提出算法的具体分割效果。

由图4b）可以看出，单独应用标记分水岭分割在面临球团矿表面凹凸不平，黏连严重的情况时，会产生很多的过分割，并且部分区域存在黏连球团未成功分割的现象，造成分割误差值相对偏高。图4c）使用传统遗传算法会存在分割结果不稳定，导致分割效果很差的极端情况；图4e）使用的改进遗传算法结合最大类间方差法虽然相比传统遗传算法减少了分割时间，提高了一定的分割精度，但还是存在部分球团矿边缘黏连尚未分割的现象。图4d）使用的改进遗传算法结合最大熵阈值法对黏连球团矿分割效果较好，误差为12.7%。误差主要是由于边缘的过分割导致了检测粒径与实际粒径误差偏大。图4f）使用的本文分割方法误差为6.8%，不仅能有效分割图4e）中未分割的黏连球团矿，并且相比图4b）和图4d）分割算法，所产生的过分割现象最少，分割效果最为理想。

为了更好地量化分割效果，本文采用分割误差指标和对以上几种分割方法的分割效果进行评估。分割误差[14]P定义如下：

式中：Pi为球团矿各个粒级的分割误差；Ns为各个粒级识别出来的球团矿个数；Na为对应粒级手动筛分出的球团矿数目。

图4 球团矿原图与分割结果图

几种分割算法分割结果量化表如表1 所示。

表1 分割算法效果评估表

采用改进遗传算法对球团矿先进行一次预分割，虽然总体耗费时间相对单一的分割有所增加，但是由于改进遗传算法加快了阈值分割的速度，所以总体耗时相对单一标记分水岭分割法增加并不多，约为0.18 s。

4 结 论

单一的球团矿分割方法直接应用在球团矿图像上效果不佳，本文先使用改进遗传算子的遗传算法与最大类间方差法进行预分割，再对分割后的二值图像采用标记分水岭分割算法进行二次分割。实验结果表明，所提方法改善了传统阈值分割方法对黏连球团分割效果不佳和减少了单独应用分水岭算法产生的过分割现象，同时耗时增加也在可接受范围内，能够为后续的球团矿质量分析提供一定帮助。