山区大跨径钢筋混凝土拱桥扣索索力优化分析研究

黄香健　王华

摘要：大跨径钢筋混凝土拱桥进行悬臂浇筑时，需要通过合理的扣索索力来保证拱肋线形以及受力处于可控范围。文章建立全桥有限元模型，引入弹性-刚性支撑法以及优化理论，对施工期扣索索力进行了计算分析。通过施加计算优化后的索力值，成拱后拱圈挠度平缓，拱顶附近挠度平均减幅为5.4%;施工中拱肋应力处于上下波动状态并最终趋于全截面受压，优化后应力最大值减小，截面受力更为均匀合理。研究结果表明，弹性-刚性支撑法与优化理论相结合，更好地兼顾拱圈施工中的变形及受力，可作为扣索索力计算参考。

关键词：悬臂浇筑;扣索索力;弹性-刚性支撑;索力优化

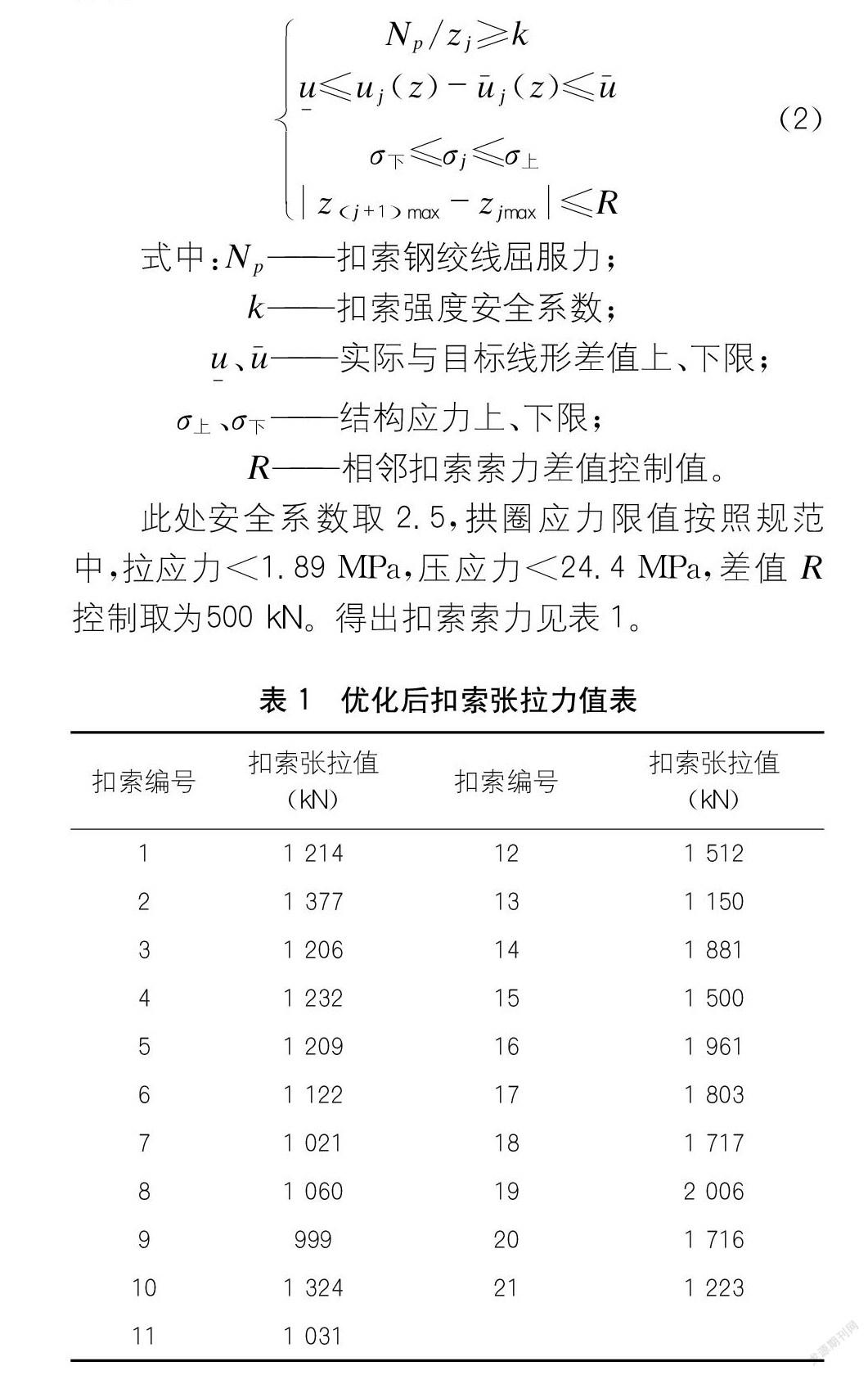
中国分类号：U443.38文章标识码：A140514

0 引言

目前拱桥悬臂施工建设中，主要采取拼装法以及现浇法，前者多见于钢拱桥，后者主要应用于钢筋混凝土拱桥中。悬臂浇筑施工多采用斜拉扣挂方式，以保证拱圈成拱状态下线形以及受力符合要求，合理的扣索索力可以使得拱圈成拱时的目标状态达到最优。根据众多学者所做的研究，扣索索力主要有零位移法[1]、零弯矩法[2]、力矩平衡法[3]、正装迭代法[4]以及优化算法[5-6]等。上述方法中，零位移法很难使得扣索理论倾角与实际相符，同时索力计算值容易出现受压情况，这在实际中是不可能发生的;零弯矩法则没有将拱肋施工时的切位移考虑在内，同时求出的索力会以负值出现而失真;力矩平衡法多用于初始索力计算，且线形控制无法完全满足目标状态;正装迭代法通过模拟实际施工工序，结合影响矩阵迭代达到成拱状态，迭代次数较多，迭代初值选择要求较高。

本文运用Midas有限元软件建立拱桥施工节段模型，选择弹性-刚性支撑法[7]计算扣索初值并进行了索力优化，分析优化后的索力以及拱圈受力状态结果，可以用于指导现场施工及计算工作。

1 工程概况

某在建钢筋混凝土拱桥净跨225 m，净矢跨比为1/6，主拱圈为拱轴系数m=1.74的等高截面悬链线拱，主拱圈采用挂篮悬臂浇筑法施工。拱箱为单箱双室结构，高4.1 m，宽10.0 m，拱上排架为双柱式，均采用现浇法施工，拱上矮T梁跨径为16 m，梁高100 cm，由9片梁组成，采用预应力后张法设计，结构型式为先简支后桥面连续结构。拱圈采用C55强度混凝土，T梁为C50强度，扣索、锚索采用高强低松弛钢绞线，抗拉强度标准值[WTBX]fpk=1 860 MPa，弹模E=1.95×105 MPa。其斜拉扣挂布置图如下页图1所示。

2 有限元模型的建立

根据设计中的结构参数以及施工顺序建立全桥施工正装模型，扣索、锚索采用只受拉桁架单元模拟，其他各结构均使用空间梁单元模拟，锚索一端固结，一端与塔上扣点连接，扣索与拱圈采用刚性连接，交界墩墩底与拱圈底部边界全约束。为了保证模拟精确性，拱圈施工共分成87个阶段，全桥全过程共划分为105个施工阶段，离散为913个节点、909个单元，拱圈施工有限元模型见图2。

3 扣索索力计算及优化理论

3.1 扣索索力计算

根据文献[7]中所描述的内容，采用弹性-刚性支撑法进行索力初步计算的结果，在施工阶段中变化较为均匀，无突变情况，其拱圈拉、压应力情况较为合理，本文在初步计算扣索索力时采用此方法结合有限元模型进行计算。弹性-刚性支撑法核心思想是，随着浇筑节段的不断增加，通过改变不同施工阶段不同扣索的刚度值获取索力初始值及增量，最后在合龙完成后将各扣索索力初值与变化累计值进行叠加，获取最终扣索索力以及相应节段预抬值。其步骤简述如下[8]：

（1）在进行第一节段浇筑完成后，结构在自重作用下，将1号扣索轴向刚度值EA调整为无穷大，计算出1号索初张力T1，1以及节段位移[WTBZ]Δ1，1。

（2）在第二节段浇筑完成后，2号扣索轴向刚度为无穷，此时1号扣索按照实际轴向刚度值进行修改。通过计算可以得出2号扣索的初张力T2，2以及节段位移[WTBZ]Δ2，2，同时节段数量增加导致1号索股索力增加T1，2和节点位移[WTBZ]Δ1，2。

（3）由此进行类推，计算出浇筑第三、四……节段索力增量[WTBZ]ΔTi，j以及各节段位移[WTBZ]Δi，j。

（4）在最后合龙的扣索力为上述每根扣索索力初值与增值叠加，松索后状态等同于将扣索力反向施加于拱圈上，得出内力及变形情况。

根据以上思路进行计算，汇总所有扣索的初值以及在每个施工阶段的索力增值，得出最终扣索张力值：

3.2 扣索索力优化

上述方法计算所得索力虽较为符合实际施工的数值，但是通过相关文献[9]可以看出，上述方法会导致最后浇筑数个节段应力出现超标现象，因此计算索力的方法需要进一步优化。

为了保证优化后截面应力满足设计要求，在构建约束条件时需要将拱肋应力作为控制要素之一，同时通过构建位移关系函数作为优化目标，使得成拱时拱圈线形满足设计要求。其构建过程如下[10]：

优化变量为扣索索力，即z={z1，z2，…，zj，…zn}T;

4 拱肋计算结果分析

4.1 拱肋线形结果

为了探明优化后的索力对于成拱时线形的影响，将优化前后拱圈整体线形进行对比，见图3。由图中曲线变化趋势可以看出，优化后挠度曲线相较于优化前更加平顺，无明显突变处，1/4拱肋截面至拱脚处相对于优化前有些许增大，拱顶附近挠度优化后总体有所减小，平均减幅为5.4%。总体来看，优化后的挠度虽在跨中有所增大，但是仍然满足要求，且整体挠度变化平缓，避免了因变形不一致导致的结构附加应力的出现。

4.2 拱肋应力结果

为了分析关键截面处应力施工过程的变化情况，分别选取1/8拱肋截面以及1/4拱肋截面的优化后应力值，绘制变化情况如图4所示。从图4可以看出，两个位置截面上、下缘应力相互交错波动，张拉扣索时，扣索力使得扣點附近的节段出现明显的下缘趋向于受拉、上缘受压。但由总体趋势来看，都是逐步向压应力转变，最终成拱时表现为全截面受压。

对关键截面应力变化情况进行分析后，初步掌握了截面施工全过程受力规律，同时对于优化后的各节段最大应力情况需要进一步研究。如下页图5所示，提取优化前后各节段拱圈施工中，顶板、底板最大拉、压应力值，绘制曲线图。从图5可以看出，优化后顶板、底板拉应力最大值较为均匀，波动幅度减小，顶板拉应力减小0.1 MPa左右，底板拉应力最大减小约32.6%;对于顶板、底板压应力，优化后更多的是改善了截面受力状态，底板压应力减小，顶板压应力增大，截面上、下缘应力最大差值减小约1.7 MPa，减幅达38.9%，截面受压更为均匀，受力更为合理。

5 结语

本文运用Midas有限元软件建立全桥模型，引入弹性-刚性支撑法及优化理论对施工期扣索索力进行计算，从主拱圈挠度及应力等结果进行分析，形成如下结论：

（1）结合曲线变化趋势可以看出，优化后挠度曲线相较于优化前更加平顺，无明显突变处，1/4拱肋截面至拱脚处相对于优化前有些许增大，拱顶附近挠度优化后总体有所减小，平均减幅为5.4%。

（2）拱圈应力在施工中处于波动状态，总体趋向于整体受压状态，优化后节段最大拉、压应力有一定的减小，底板拉应力最大减小约32.6%，截面受力状态得到改善，更为均匀合理。

（3）弹性-刚性支撑法结合优化理论可以更好兼顾拱圈施工期间的变形及受力情况，成拱状态下，拱肋位移值及受力情况达到预期目标，此方式可供相关学者参考。

参考文献：

[1]张克波，王国俊.大跨度钢管混凝土拱桥拱肋吊装中的扣索索力计算[J].长沙理工大学学报（自然科学版），2005（4）：17-21.

[2]周水兴，江礼忠，曾 忠，等.拱桥节段施工斜拉扣挂索力仿真计算研究[J].重庆交通学院学报，2000（3）：8-12.

[3]张克波，王国俊.大跨度钢管混凝土拱桥拱肋吊装中的扣索索力计算[J].長沙理工大学学报（自然科学版），2005（4）：17-21.

[4]徐 岳，申成岳，朱谊彪，等.确定拱桥斜拉扣挂施工扣索张力的改进迭代算法[J].桥梁建设，2016，46（2）：65-69.

[5]张治成，叶贵如，王云峰.大跨度拱桥拱肋线形调整中的扣索索力优化[J].工程力学，2004（6）：187-192.

[6]田仲初，陈得良，颜东煌，等.大跨度拱桥拱圈拼装过程中扣索索力和标高预抬量的确定[J].铁道学报，2004（3）：81-87.

[7]田仲初.大跨度钢箱拱桥的施工控制关键技术与动力特性研究[D].长沙：中南大学，2007.

[8]何 畏，周伟光，陈俊诚.悬臂浇筑拱桥扣索索力优化研究[J].桥梁建设，2015，45（3）：32-36.

[9]田奇龙.大跨径上承式混凝土拱桥扣索索力计算与优化[J].公路与汽运，2018（3）：122-126，132.

[10]朱连伟，邓年春，于孟生，等.600 m级拱桥斜拉扣挂施工扣索索力的正装迭代优化算法[J].铁道建筑，2020，60（12）：18-21.

3403501908217