制导率未知时返回弹道自适应抗差滤波计算
2021-03-16李恒年麻蔚然
淡 鹏,李恒年,麻蔚然,王 丹
(1. 宇航动力学国家重点实验室,陕西 西安 710043;2.西安卫星测控中心,陕西 西安 710043)
0 引言
航天器返回过程弹道计算[1-2]是其落点预报的基础,为落点预报提供初始位置速度,因而在返回任务实施过程中有着重要意义。外测跟踪数据是返回过程的一类重要跟踪数据,但其观测量一般为测站地平坐标系下的测距、方位角、仰角及测距变化率数据,要将其转换出含有x,y,z三个分量的速度数据还需要采用滤波等其他较复杂的计算方法。
在航天器升力式返回地球过程中,为使其着陆于事先设定的区域,常常需要进行制导控制[3-5],不同的制导率设计对飞行弹道及落点位置的影响巨大,且一些航天器返回过程制导方法设计较为复杂,使其飞行过程受力情况变化明显,给制导率未知时的返回弹道估计带来困难。
针对此类不能准确建立外推模型的机动[6]过程滤波问题,常用的计算方法是采用当前统计模型、多项式模型等,文献[7-9]对该2类模型进行探讨,但当前统计及多项式模型对观测数据的变化较为敏感,抗差性稍差。文献[10]在横向和纵向上建立再入目标模型,并引入一种改进的自适应无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法,但该方法不适用于需要计算三维位置速度分量的情况;文献[11]将重点放在了各种滤波方法使用上,对模型建立方法考虑较少;文献[12]采用3站测距、测速及UKF滤波算法估计再入弹道,但不适用于少于3站测量的情况。
针对这些情况,在李恒年等人[13-14]提出的变质量动力学模型基础上,对其进行扩充和自适应改进处理,并采用UKF方法,实现对制导率未知状态下的返回弹道位置速度三维分量的自适应抗差估计计算。
1 滤波计算模型
1.1 滤波算法
目前常用的滤波计算框架有扩展卡尔曼粒子滤波(Extended Kalman Particle Filter,EKPF)、UKF、容积卡尔曼滤波(Cubature Kalman Filter,CKF)和粒子滤波(PF)等,EKPF易于实现,但其线性化过程会引入模型误差,且需计算非线性函数的Jacob矩阵;CKF采用等权值的一组采样点进行滤波计算,虽然计算量较UKF小,但实际计算表明,因各采样点等权值,使得某些状态下可能使非线性滤波的稳定性减弱;PF实现稍显复杂,故本文采用UKF算法。
UKF算法基本方法如下:

状态估计协方差为(Q为状态噪声协方差阵):

观测量预测值为:
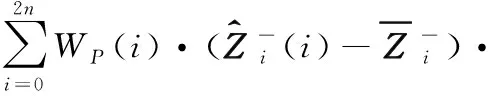
状态向量与观测向量之间相关协方差矩阵为:
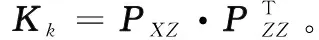
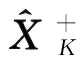
1.2 状态模型
以文献[13]中的机动推力下的滤波状态模型为基础,建立系统状态模型,由于原模型在计算加速度时,需要使用姿态信息,增加了算法的局限性。为此,此处将该模型中的加速度项进行三维扩展,在J2000惯性系下建立滤波系统状态向量为:
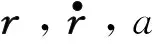

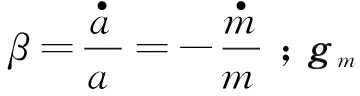
1.3 观测模型
由于外弹道测量数据中各类观测数据质量不一,一般情况下测距数据质量较高、而测角数据质量较差,为此,滤波时将观测模型建立在测站地平坐标系下,以便充分利用不同精度的观测量。则观测方程为:
1.4 起步计算
再入过程外测跟踪数据建立在测站地平坐标系下,无法直接转换为J2000坐标系下的位置速度,但可以由测距、测角值计算出位置矢量。据此,可用多个点进行起步,并使用二次或三次多项式在x,y,z各分量上进行多项式拟合,进而由最小二乘算法计算出拟合点的位置分量变化(速度)值。状态向量起步值中后4项可给定为0。
2 自适应滤波计算
由于返回过程制导率未知,即存在未知的机动过程,导致动力学模型不能反映实际飞行状态,为此,需要对滤波过程进行自适应处理。
此处采用2种自适应处理方法,并对其应用效果进行探讨。
2.1 基于机动检测及模型切换的自适应处理
机动检测[15]的基本思想是,机动发生时目标的状态估计将出现偏差,导致滤波的新息(残差)序列统计特性发生变化。为此,可根据滤波新息构造二阶统计特性,来实现机动的检测。

对于新息序列,D(k)服从自由度为m的X2分布。当机动发生时,新息序列的统计特性发生变化,不再是均值为零的高斯白噪声,D(k)值可能出现较大的变化。为此,可根据返回弹道特性,对D(k)值设置一定的检测门限,当多个点的D(k)值连续超过该检测门限时,认为发生机动不采用单点检测的原因在于观测数据中可能存在野值,会影响判断的准确性。实现时,可采用多点滑窗方法对D(k)值序列进行检测。
当检测出机动发生时,通过调整滤波参数P和Q来完成不同模型的切换,使其滤波状态快速适应机动变化。
在连续多点D(k)值变化较大,且持续时间较长时,可通过重启滤波器的方法来实现更快的收敛及对发散的抑制。
2.2 基于加速度模型补偿的未知机动自适应处理
机动发生时,UKF的状态模型将与实际情况不匹配,则在滤波计算中,若将Q矩阵设置为固定值,则可能与实际飞行变化出现较大偏差,导致滤波不能适应机动变化,可能需要较长时间才能收敛,甚至会出现滤波发散情况。为此,考虑对滤波过程的状态噪声协方差矩阵Q进行实时补偿,来自适应未知机动的发生。
考虑到机动发生时,加速度发生较大变化,状态模型中的加速度项将与实际情况不符,因而对Q的实时补偿将重点放在加速度分量的补偿上。


加速度模型误差近似值为:
进而,对状态噪声协方差矩阵更新为:
式中,λ为弹道机动频率系数(0<λ<1),可取固定值(如0.001)。当机动加速度小时,或需要提高抗差效果时,λ应取小量。
这样,即可由采样点状态量预测均值和滤波状态量改进值实现对状态协方差矩阵的自动更新。
3 计算及分析
为了测试制导率未知状态下返回弹道自适应滤波算法的适应性及应用效果,分别采用当前统计模型EKF算法、基于机动检测及模型切换的自适应滤波算法(此处记为MOUKF),基于加速度模型补偿的未知机动自适应滤波算法(记作COUKF)等3种算法进行返回过程弹道滤波计算。以某次卫星理论返回弹道为基础,仿真多个连续接力的测站的外测跟踪数据,并为测距、方位角、仰角和测距变化率分别加上10 m,0.01°,0.01°,0.01 m/s的随机噪声(1σ)。
3种算法计算的弹道近地点高度及理论曲线局部图如图1和图2所示(该曲线相对于高度曲线,对滤波稳定性及适应性反应更加明显)。

图1 Hp曲线第一段局部放大图Fig.1 Partial enlarged drawing of the first section of Hp curve
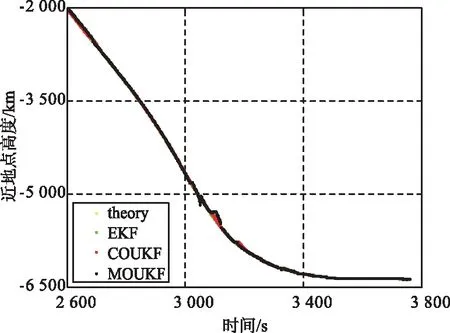
图2 Hp曲线第二段局部放大图Fig.2 Partial enlarged drawing of the second section of Hp curve
由计算可知,MOUKF和COUKF均能够自适应返回段飞行弹道的变化,曲线震荡幅度均小于EKF。但MOUKF对机动适应能力没有COUKF强,出现了多次曲线分段或重起步的现象。而COUKF在自适应性、抗差性等方面均表现出了较好的适应能力,且实现过程比MOUKF简化。
为测试COUKF中加速度机动系数λ的影响,对λ分别取0.000 01和0.001,所得到的近地点高度曲线变化如图3所示。
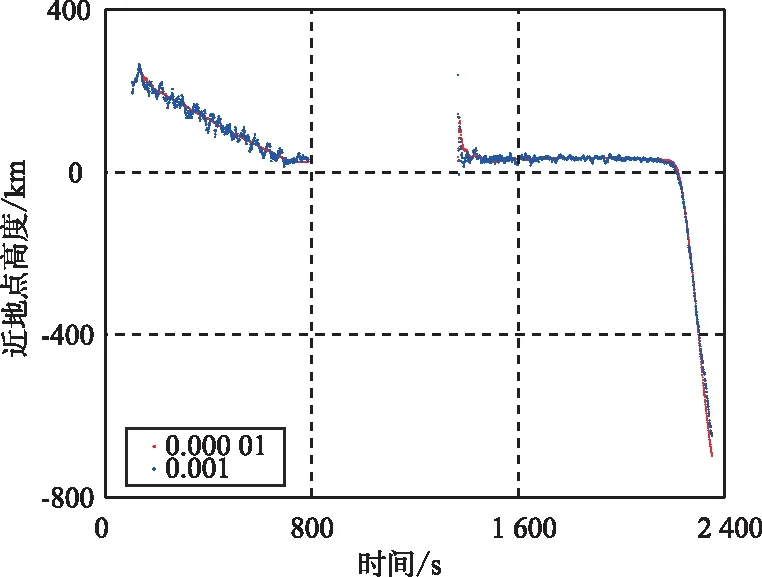
图3 机动系数影响对比Fig.3 Comparison of the influence of maneuver coefficient
由图3可以看出,λ取值小时,滤波震荡幅度更小,抗差能力更强;但取值大时,对机动的反应更加迅速。使用时可根据弹道特点合理取值。
4 结束语
针对外测跟踪下的制导率未知状态下返回弹道自适应滤波问题,建立了包含10维数据的状态模型,并分别采用基于机动检测及模型切换的滤波算法、基于加速度模型补偿的未知机动滤波算法进行了自适应计算。从计算结果可以得出:
① 文中给出的滤波计算状态模型及观测模型是可行的,滤波算法虽然未采用制导率建立外推模型,但仍然能够有效适应返回弹道的飞行特点;
② 文中给出的基于机动检测及模型切换的自适应处理方法、基于加速度模型补偿的未知机动自适应处理方法是可行的;
③ 基于加速度模型补偿的未知机动自适应处理方法在对机动的适应能力上优于基于机动检测及模型切换的算法,且比后者更易于实现;
应该看到,制导率未知状态下返回弹道的计算是一个较复杂的工程问题,实际飞行状态及观测数据质量可能出现异常或较大偏离等情况。下一步将重点放在算法的健壮性及优化上开展研究。
