基于VSC等效阻抗的STATCOM优化配置

宁 波

（国网湖北省电力有限公司直流运检公司，湖北 宜昌 443000）

0 引 言

柔性交流输电系统（Flexible AC Transmission System，FACTS）能够有效改善电力系统的参数分布，确定FACTS控制器的最佳位置具有重要研究价值[1-3]。FACTS补偿器的优化配置虽然有效地改善了电力系统的不同参数[4,5]，但是流方程和FACTS控制器建模非常耗时[6,7]。因此，应用传统方法来解决FACTS的最优分配是不适用的。为此，本文在当安装FACTS装置时，利用灵敏度分析来减少VSC和FACTS设备所需的计算时间，并确定控制变量和观测变量之间的直接关系。除此之外，还需对与FACTS装置分配相关的优化问题进行VSCS的间接建模，从而优化系统的潮流计算和VSCS的精确建模。

1 VSC的等效阻抗建模

系统和STATCOM之间交换的无功功率可通过等效阻抗（并联）进行建模，连接到节点的等效电压源和等效阻抗示意如图1，图2所示。

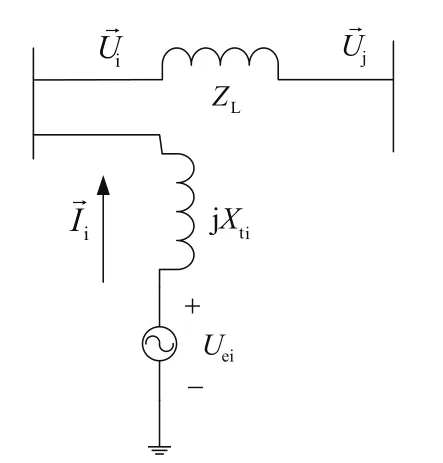
图1 STATCOM等效电压源示意图

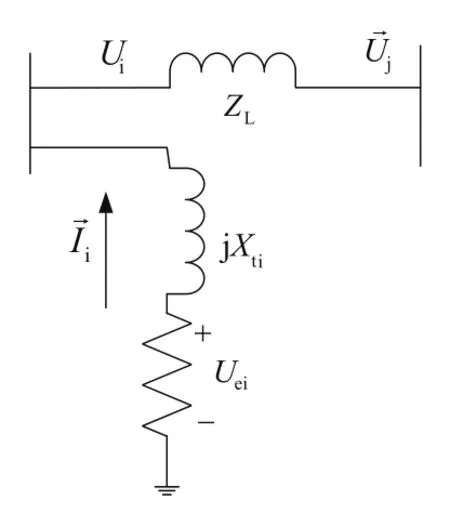
图2 STATCOM等效阻抗模型示意图

STATCOM等效阻抗的计算关系如下：

通过使用上述方程，计算得出导纳变化矩阵，如公式（3）所示。然后得到母线的修正电压，根据母线电压计算来引入目标函数的不同参数。

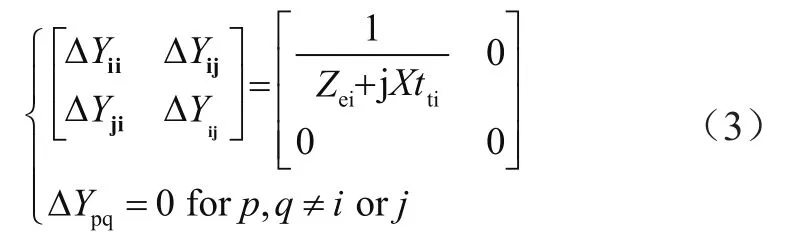
式中，ΔY为导纳变化矩阵。

为了求得补偿电压，电压变化矩阵应满足：

电流矩阵可按式（5）计算：

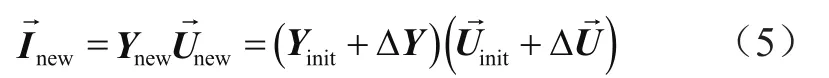
对式（5）进行扩展得到：

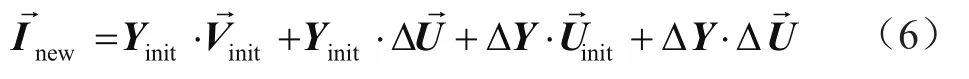
假设与通过系统线路的主电流相比，补偿器注入的电流可以忽略不计。因此，补偿和初始电流矩阵两者相等。此外，电压和导纳变化矩阵的乘积约为零，其表述为：

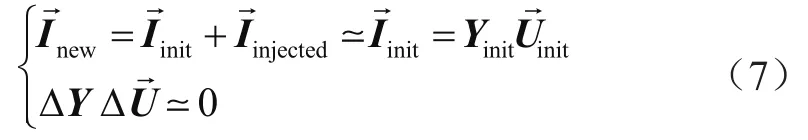
根据上述方程，可得出式（8）：

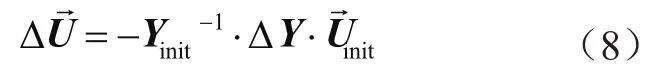
通过等效模型计算和灵敏度分析来找出系统初始状态的潮流结果。然后，计算导纳变化矩阵ΔY，进而可以计算电压变化Δ。在每次迭代结束时，将电压变化与之前的变化进行比较。如果母线电压变化近似恒定，则停止计算，输出结果。从而确定了导纳变化和由补偿器引起的电压变化之间的关系。

2 目标函数与优化过程

为了优化FACTS设备的配置，选择了不同的特性和指标来改善电力系统不同点的电压分布。除了电压分布，传输能力是影响系统可靠性和性能的另一个指标。此外，相位角δ是影响暂态稳定性的重要参数。如果δ减小，传输线的稳定裕度将提高。3个系统参数电压分布、线路传输能力和相位角如式（9）所示：

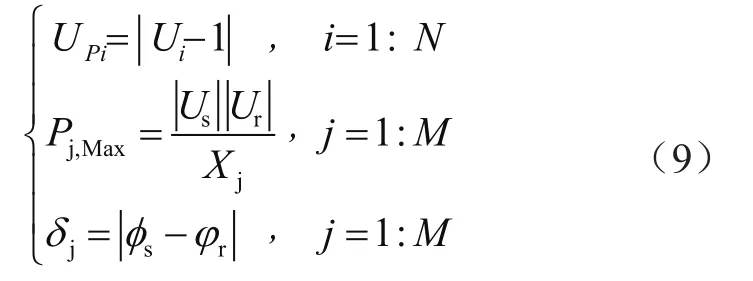
式中，UPi为节点i和参考值的电压幅值之差；Pj,max为连接两个节点i和j的线路有功功率传输能力的最大值；δj为连接两个节点i和j的电压相角之差。

本文提出了一种基于VSC等效阻抗建模的STATCOM优化配置的目标函数，即

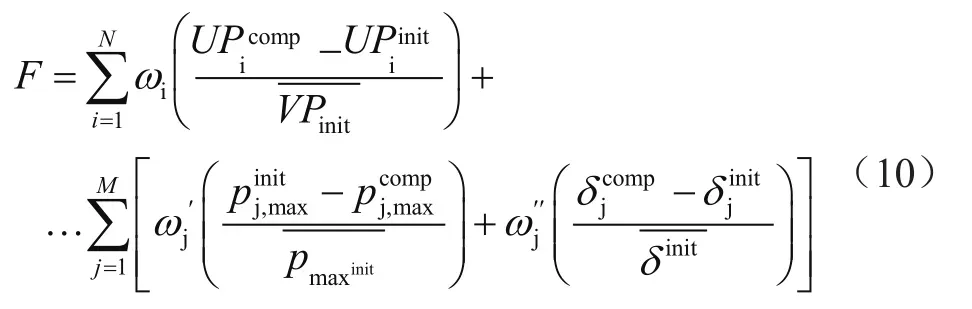
式中，Pj,max为线路j的最大可传输有功功率；分别为 Pj,max最大值的初始值和补偿值；ωi为目标函数电压分布指数的节点i的权重系数；ωj'为线路j传输能力指数的权重系数；ωj''为线路j相位角指标的权重系数；N为系统节点的数量；M为系统线路的数量。

所提出的目标函数的不同指标和适当的加权系数创建了适当的STATCOM配置。权重系数决定了电压分布、传输能力和相位角之间的相对重要性，并建立了它们之间的合理关系。为了解决基于式（10）所示目标函数的优化问题，采用遗传算法（Genetic Algorithm，GA）来进行求解。得到的最优解决定了STATCOM的位置和每个补偿器的VSC的大小。

3 算例分析

选择了一个典型的6节点电力系统来验证所提出的方法，参数如表1，表2所示。

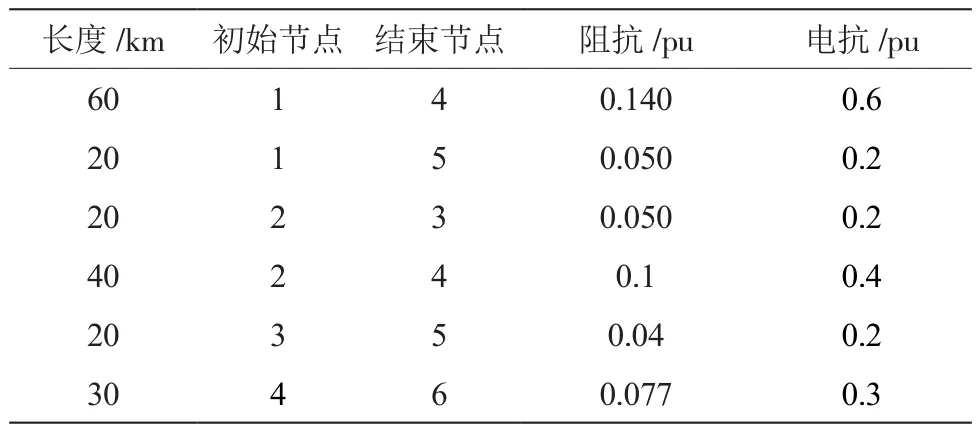
表1 6节点电力系统参数

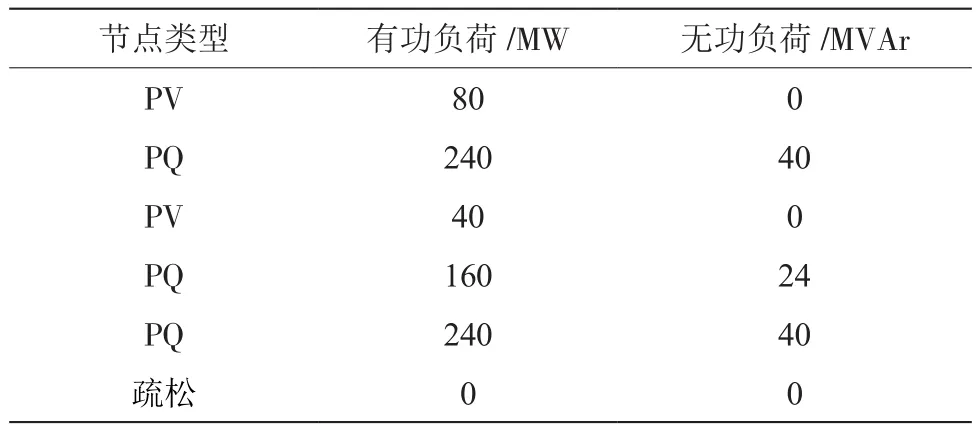
表2 6节点电力系统负荷数据

首先，需要得到基本情况下电力系统潮流计算结果，基本情况下的潮流结果和拟定目标函数的3个重要特征如表3、表4所示。

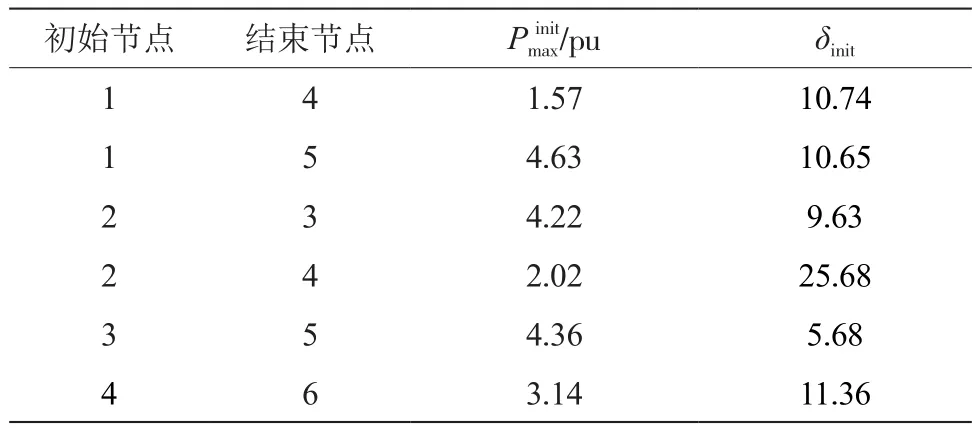
表3 传输能力和相角

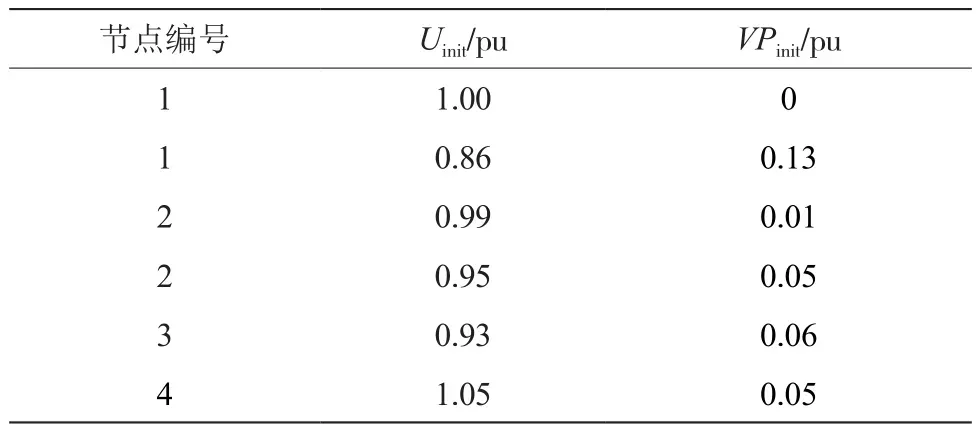
表4 电压分布

根据系统的基本参数，假设可以实设置个STATCOM来改善系统参数。等效阻抗模型和灵敏度分析已用于计算安装STATCOM的影响和目标函数。然后利用遗传算法对优化问题进行求解，并在MATLAB的优化工具箱上实现了遗传算法。优化结果如表5所示。

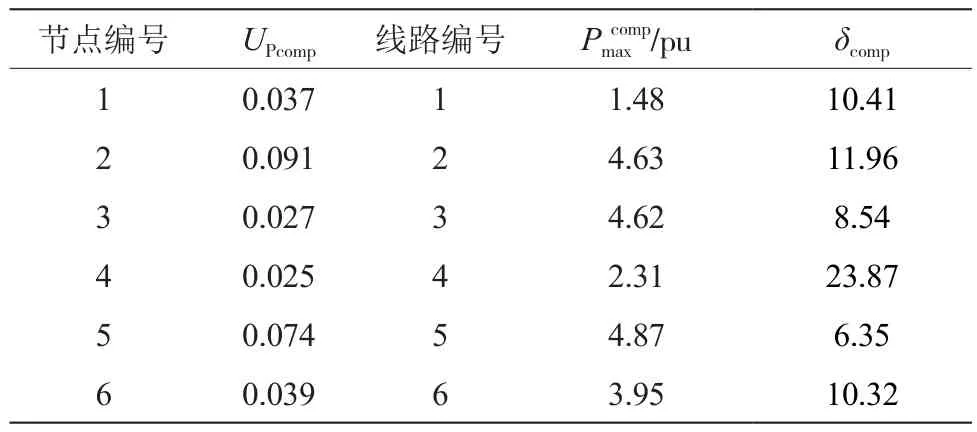
表5 STATCOM的最佳配置结果

从表5可以看出，补偿电压剖面和相位角的值已减小到更好的状态。此外，线路的最大传输能力也得到了提高。最佳目标函数值为-0.631。此外，STATCOM的最佳配置利用位于节点1、5和6中的3个STATCOM电压值分别为1.04 pu、0.94 pu和0.92 pu。

4 结 论

FACTS补偿器的优化配置虽然有效地改善了电力系统的不同参数，但是流方程和FACTS控制器建模非常耗时。为了补偿系统参数，改善系统性能，本文提出了一种基于灵敏度分析和等效阻抗模型的STATCOM优化配置方法。由于该方法不需要在每次优化迭代中求解潮流，也不需要对FACTS进行精确建模，因此具有时间效率和实用性。