低符号速率下的大多普勒频偏信号的频偏估计

张少侃，梁中英，高心炜

（广州海格通信集团股份有限公司，广东 广州 510663）

0 引 言

在目前的数字通信系统中，通信收发双方硬件时钟的稳定度和准确度不可能完全一致，且通信双方的相对物理运动会使空中传输的无线电波产生多普勒频移，造成了接收信号和发送信号的载波频率存在一定的偏差。因此在接收处理中，频偏估计模块是数字通信系统的重要组成部分。

在数字通信系统中，根据通信系统是否有导频数据，可将频偏估计方法分为数据辅助和非数据辅助两大类。在数据辅助的频率偏差估计方法中，数据流中往往会有规律地插入已知的独特码以供接收端进行频偏估计处理，实际应用的通信工程项目中常用的数据辅助频偏估计算法有Kay算法、Fitz算法、M&M算法、L&R算法以及基于FFT频偏估计算法[1-5]。在非数据辅助的频率偏差估计方法中，数据流中未插入收发端均已知的独特码字供接收处理利用，甚至接收方都不知道无线信号的调制方式、符号速率等，这时便给频率偏差估计带来了极大的挑战与困难。大多数通信系统针对多进制数字相位调制（Multiple Phase Shift Keying，MPSK）信号使用非数据辅助频偏估计算法进行频偏估计。对于MPSK调制信号，可以通过幂次方运算或非线性变换法去除调制信息，然后使用上述常见的数据辅助频偏估计算法进行频偏估计[6-8]。

对于数据辅助的频偏估计算法，其估计的频偏精度高，而且可估计的频偏范围大。例如，基于FFT频偏估计算法的精度与快速傅里叶变换（Fast Fourier Transformation，FFT）的点数有关，FFT变换的点数越多，则精度越高。可根据实际需要来设置FFT变换点数以达到系统的要求，其可估计的频偏范围能够达到（-fs/2，fs/2），其中fs是通信系统的符号速率。而对于非数据辅助频偏估计算法，其频偏估计精度比数据辅助频偏估计算法低，估计范围比数据辅助频偏估计算法小。例如，对于MPSK调制信号，经过幂次方运算后，其频偏估计精度会随着噪声增加急剧恶化，而且经过幂次方非线性变化后，其频偏估计范围变为（-fs/2M，fs/2M），频偏估计范围缩小了M倍。从以上分析可看出，非数据辅助的频偏估计算法存在着频偏估计精度低和频偏估计范围小等缺点。

对于窄带通信系统，系统频偏较大，频偏会远远超过数据辅助频偏估计算法和非数据辅助频偏估计算法的估计范围。因而对于窄带通信系统，频偏估计的范围是需要重点考虑的问题。本文提出的频偏估计算法可以很好地解决频偏估计的范围问题，这是因为其频偏估计范围不受系统符号速率的限制，而且频偏估计的精度适中。对于频偏估计精度要求较高的低速率通信系统，可以首先使用本文给出的频偏估计方法估计出一个粗频偏值，然后根据系统的具体情况选择数据辅助频偏估计算法以达到系统的整体性能要求，这样就可以同时解决系统频偏估计的大范围和高精度问题。由于此种频偏估计算法不受系统符号速率的限制，因而可以很好地解决低信噪比（Signal-to-Noise Ratio，SNR)下低符号速率系统频偏过大的问题。目前，此种算法已经应用到多个实际工程项目中，均得到了较好的性能效果。

1 信号模型

以MPSK信号为例，其信号解析表达式为：

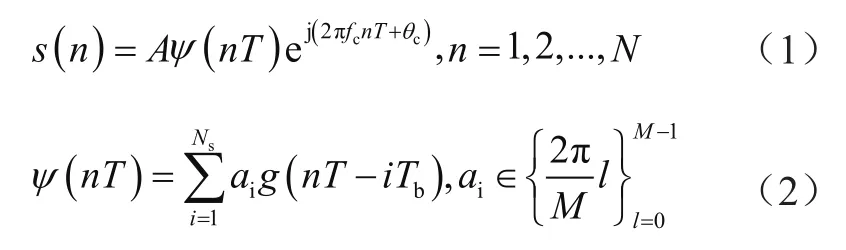
式中，A为信号的幅度，N为样本点个数，T为采样时间间隔，Ns为码元个数，Tb为码元的宽度（单位是采样点个数），g(·)为成型滤波函数，fc为信号的载波频率，θc为信号的载波初始相位。

假设信道为加性高斯信道，则接收到的信号可表示为：

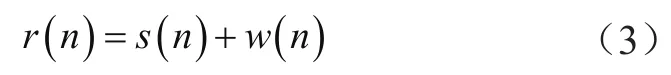
式中，w(n)为高斯白噪声。

2 频偏估计算法分析

当通信系统的接收端信号存在载波频偏时，这时接收到的信号可以表示为：

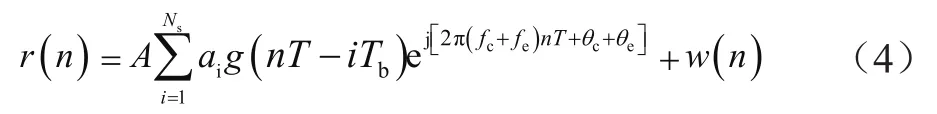
式中，fe表示收发端之间的频率偏差，θe表示相位偏差。由于w(n)为加性信道高斯白噪声，因此其频率谱线是一条均匀的定值线。然而载波频率表达式却多出了频偏fe，直观显示在接收端信号频率谱线图上便是接收信号的频率谱线整体平移了fe。利用此特征，只需找到接收数字信号频率谱线整体偏移值便可获得收发信号的载波间偏移量fe，这便是本文提出的频率偏差估计算法的理论基础。从这个原理上可以看出，通信系统收发双方的载波频偏fe与系统符号速率无关，因此本文提出的频偏估计方法所能估计的频偏范围与系统符号速率无关。但是在SNR情况下，信号几乎被噪声淹没，因而频偏估计问题就转化为SNR下如何有效抑制噪声的问题。

2.1 滑动平均滤波处理

使用滑动平均滤波可使信号频谱变得平滑，为了工程实践的简单起见，用文献[9]给出的信号频谱滑动平均滤波公式，即：

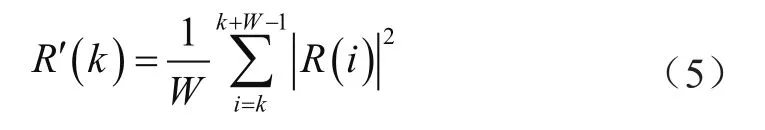
式中，R(i)为接收信号r(n)的频谱函数，W为平滑滤波的窗长度，R'(k)为平滑滤波后的输出信号频谱。通过滑动平均滤波处理可在信噪比极低情况下很好地改善接收信号的频率谱线图。例如，假设发端使用四相移相键控（Quadrature Phase Shift Keying，QPSK）信号，其接收端信噪比设置为-7 dB，得到的接收信号频率谱线和滑动平均滤波后的信号频率谱线如图1所示。从图1可看出，滑动平均滤波后的信号频谱清晰易辨识，滑动平均滤波前的信号频谱则因噪声叠加而难以辨认。

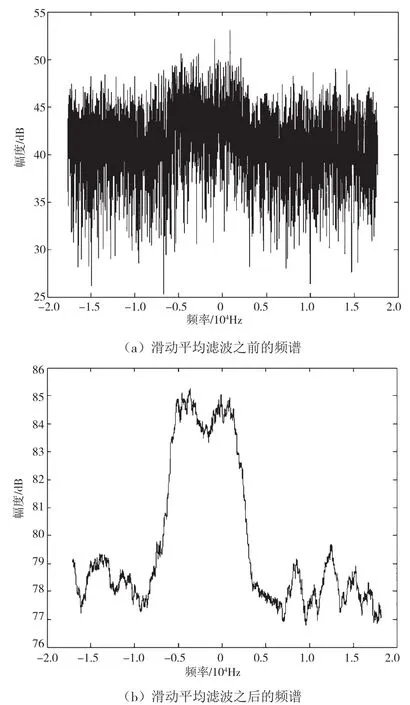
图1 滑动平均滤波前后的频谱

2.2 数据加强处理

接收信号做滑动平均滤波处理可明显改善信号频率谱线的平滑度，但由于在信噪比极低条件下，白噪声引入接收信号频率谱线的幅度波动巨大，因此使用单次FFT变换后的数据做频率偏差估计会有很大的不稳定性。为了提高估计的稳定度和精确度，本文使用频率谱线多次叠加的方法来提高信号频谱的稳定度和清晰度，其具体公式为：

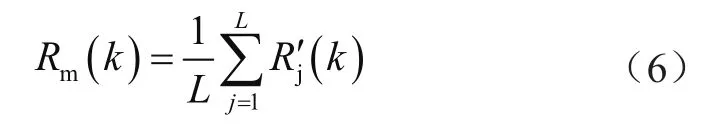
式中，L为需要叠加的FFT变换后的数据组数，R'j(k)为第j组经过平滑滤波后的FFT变换数据，Rm(k)为叠加后的信号频谱。通过优化L的数值可提升频偏估计的准确度。

2.3 频偏估计

在得到上述多组数据叠加后的稳定信号频谱后，就可以做频偏估计处理。首先需要找出Rm(k)中的最大幅值Rm(kmax)，即：

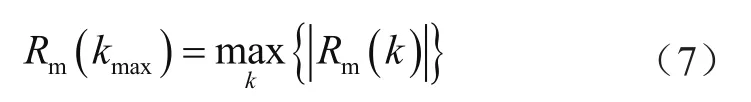
然后根据3 dB信号带宽的定义，需要找到有用信号的范围。假设k1和k2分别为有用信号通带的两个端点，则其应满足：

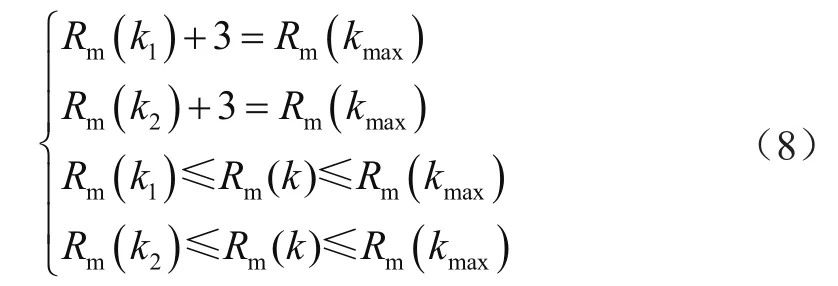
式中，频谱幅值Rm(k)的单位为dB。根据载波频率位于信号通带内的中心位置，可以求出信号中心频率的位置为：

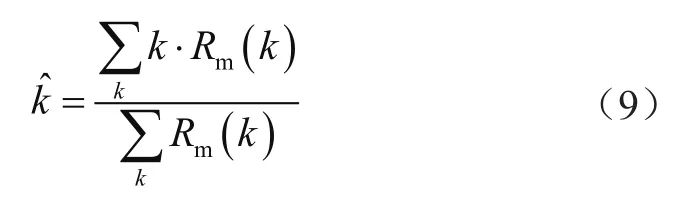
式中，R1≤R≤R2，这样估计出的载波频率为：

式中，NFFT是每组数据做FFT的点数，这样估计出的频偏为：

综上所述，本文给出的频偏估计算法的整体步骤如下。首先利用式（5）对接收到的信号频谱做平滑处理；其次利用式（6）对平滑处理后的频谱做多组数据叠加处理；再次利用式（7）和式（8）找出有用信号的通带范围；最后根据有用信号通带范围以及式（9）、式（10）和式（11）估计出信号载波频偏。

利用上面的步骤可以估计出大频偏信号的载波频偏。对于低符号速率频偏估计精度要求较高的通信系统，上述频偏估计方法给出了一个频偏粗估计值，可将通信系统的载波频偏缩小到一定的范围内。对于频偏估计精度要求较高的通信系统，可在本文给出的方法之后加入常规的频偏精估算法，以达到系统要求。

3 仿真分析

本节对本文提出的频偏估计方法进行MATLAB仿真分析。首先对频偏估计算法的频偏估计范围进行仿真分析，然后与克拉美-罗界（Cramer-Rao Bound，CRB）进行比较。文献[10]给出了MPSK信号载频估计的修正克拉美-罗界（Modified Cramer-Rao Bound，MCRB），即：

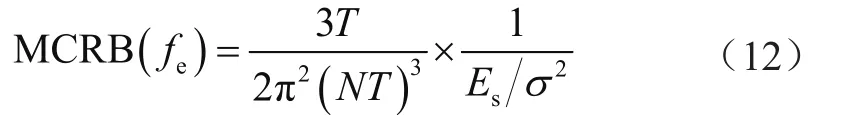
式中，Es表示每个符号的能量，σ2表示复噪声的功率。本文使用MCRB指标来对比算法的性能。

仿真时设置QPSK信号的符号速率为4 kSPS，采样速率为16 kHz，成型滤波函数选用平方根升余弦滚降滤波函数，仿真次数为1 000次。

3.1 频偏估计范围的仿真分析

设置系统频偏值的变化范围为-6～+6 kHz，设置系统信噪比SNR=-10 dB和SNR=-5 dB，使用本文给出的频偏估计方法估计出的频偏估计归一化均方根误差随系统频偏的变化曲线如图2所示。

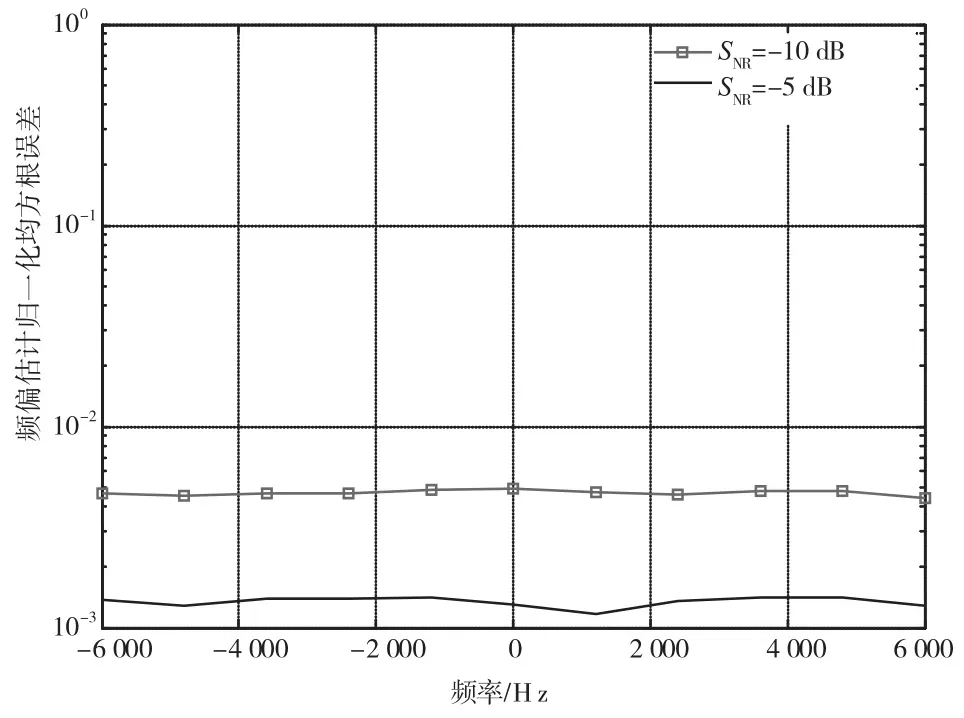
图2 归一化均方根误差曲线

从上述仿真结果可以看出，在低信噪比下，频偏值从-6 kHz变化到+6 kHz，本文提出的频偏估计方法均能有效地估计出系统载波频偏，且在SNR=-5 dB时的估计精度优于SNR=-10 dB时的估计精度。

3.2 频偏估计性能的仿真分析

设置系统的信噪比值变化范围为-10～+10 dB，使用本文提出的频偏估计算法进行系统频偏估计仿真，其频偏估计归一化均方误差与MCRB比较曲线如图3所示。从频偏估计归一化均方误差与MCRB比较曲线可以看出，随着信噪比的提高，算法的性能逐渐提高，且逐渐逼近MCRB。

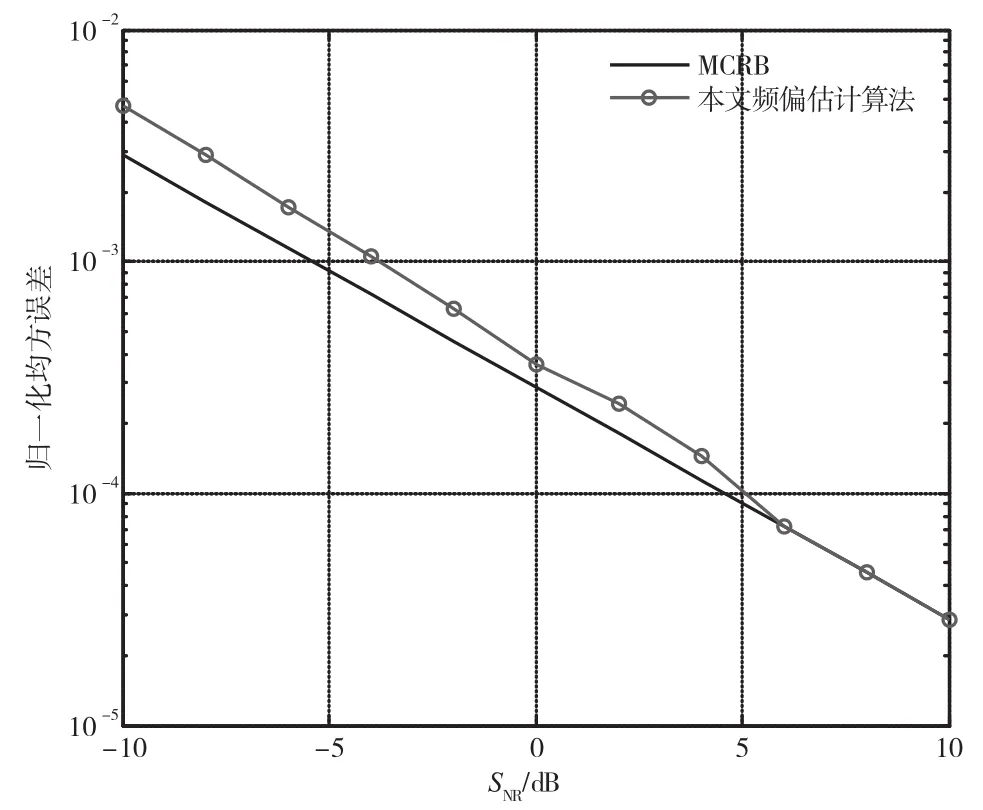
图3 频偏估计归一化均方误差与MCRB比较曲线

4 结 论

针对低信噪比下的低符号速率系统大频偏估计问题，本文给出了一种利用信号频率谱线滑动平均滤波和数据加强处理的盲信号频偏估计方法，该方法与信号调制方式无关，且估计的频偏范围不受系统符号速率限制，因而可以很好地解决系统大频偏估计问题。MATLAB仿真结果表明，随着信噪比的提高，本文算法的频偏估计归一化均方根误差逐渐逼近MCRB，且本文算法的频偏估计范围可大于系统符号速率。