基于耦合模型的地质灾害易发性分区
——以宜宾市为例
2021-03-15金帅
金 帅
(防灾科技学院,河北 三河065201)
引言
宜宾市地处云贵川三省交界地带,地震活动频繁,地震、降雨加之人为活动导致该地区地质灾害发生频繁,给人民群众生命财产带来巨大威胁。地质灾害易发性分区不仅可以有效减轻地质灾害损失,还可以为各级政府制定地质灾害防治规划和实施地质灾害预警提供依据[1]。
目前,地质灾害易发性分区方法较多,但没有统一的评价标准[2,3]。最早为方便评价,研究者试图通过模糊评判的方法进行易发性分析,此方法主观因素占主导,结果是否可信常受到质疑[2-5]。萨蒂[5]利用层次分析模型进行易发性评价,通过专家等具有专门知识的人对各评价因子进行重要程度排序,构建比较矩阵并赋予权重值。由于AHP 法往往是通过专家等权威人士进行分析,结果具有公信力[5-6]。由于易发性工作的发展,不依靠主观因素的客观评价方法开始涌现,如证据权、Logistics 模型、信息量模型等[2-3]。目前,常用的方法有信息量模型[3]、Logistics 模型[4]、AHP 法[5-6]及人工智能[7]等方法。其中,证据权法考虑了各因子正负两方面的因素,对因子如何影响滑坡发生有全面的认识,但是计算较为复杂,分区精度不高;Logistics 模型计算量较小,可以方便得到因子权重,模型建立后,只需填入各因子数值就可快速得到某地区易发性概率,但Logistics 模型对因子要求较高,各因子不得有任何相关性,实际中会导致因子选取困难;AHP 法对参与者的专业知识与经验要求极高,经验不足会导致精度降低甚至不可用;人工智能的方法计算快速且精度较高,但该方法对参数的调试繁琐,未经参数调优的模型不可用。由于信息量模型理论简单,计算方便,既有效避免AHP 法主观判断,精度又略高于Logistics 模型[8],逐渐成为易发性分区主要方法。
信息量模型优点突出但也有缺陷。其只是单纯的对各因子图层进行叠加,忽略了各因子对易发性的贡献率不同,模型加入过多非主要评价因子往往导致分区精度降低。本文针对易发性评价工作中,单一模型评价有缺陷的问题,选择常用的信息量模型与Logistics 模型进行耦合。Logistics 模型客观计算得到的系数表示了各评价因子的重要程度,利用其为信息量模型做权重,弥补信息量模型忽略各因子贡献率不同的缺陷,降低易发性次要因素比重,以此提高易发性分区精度。
1 研究区概况
宜宾市位于四川省东南,全市面积1.33 万平方公里,总人口551.5 万[9]。宜宾市地形由西南向东北逐渐降低,全市地形地貌以山地和丘陵为主,全区地质灾害点分布较为分散,但大多集中于海拔中部地区,全市海拔最高与最低处地质灾害分布较少。本文共选取宜宾市地质灾害点1160 处。其中滑坡603 处,崩塌345 处,崩塌、滑坡及具有发展成崩塌和滑坡的不稳定边坡共占地质灾害点总数的92.32%,表明研究区内主要地质灾害为滑坡和崩塌。宜宾地质条件复杂,以石英岩、页岩、粉砂岩、泥岩为主,玄武岩少量分布。
2 数据来源及因子分析
2.1 数据来源
本文地质灾害数据来源于四川省自然资源厅(http://dnr.sc.gov.cn/scdnr/scxxgkzn/sc_gkzn.shtml),利用ArcGIS转换成矢量点图层,研究区内主要地质灾害为滑坡与崩塌,经分析,地质灾害点在300m~600m 处分布最为广泛,占全区地质灾害点51.5%;地层岩性和断裂带来源于中国地质调查总局1:50 万地质图,经重投影并矢量化得来;数字高程模型(DEM)来源于NASA,采用12.5mALOS DEM,经镶嵌和裁剪后重采样为30m 栅格。地形因子(如坡度、坡向等)根据DEM 得来,其中,平面曲率表示研究区内地形离散度及水流汇集的可能性,是等高线的弯曲程度;剖面曲率表示坡度的再分析,对坡度再次求导得出,是剖面线的弯曲程度;基础地理数据如路网、水系等来源于天地图(http://lbs.tianditu.gov.cn/home.html),其中路网分为铁路网与公路网,对其进行合并处理;降雨量利用近10 年宜宾地区降水再分析数据,来源于WheatA,经计算各点平均值后使用普通克里金插值得来;地震动峰值加速度(PGA) 来源于《中国地震动参数区划图》(GB18306-2015);兴趣点(POI)密度采用爬虫技术获得宜宾地区5 万余处POI,经ArcGIS 密度计算得来;NDVI采用Landsat 8 OLI_TIRS 卫星数字产品,经辐射定标及大气校正后计算得来;地形因子(坡度、坡向等)来源于ALOS DEM,基于ArcGIS 进行提取。
综合考虑研究区实际与计算量,结合前人经验[10],本文以30m×30m 栅格为评价单元,基于ArcGIS 共划分为14738029 个栅格。
2.2 评价因子分析
目前,易发性分区因子选取种类与方法日益增多[11]。本文选取DEM、坡度、坡向、PGA、POI 点密度、地形起伏度、坡型、断层距离、河流距离、道路距离、NDVI、土地利用、岩性、降雨量、剖面曲率,平面曲率共计16 类评价因子,其中,连续型因子以自然断点法进行分级,非连续性因子以频率比作为分级依据。
DEM 越高,地质灾害发生频率越高,超过一定海拔高度后,地质灾害频率开始降低,由图1 可知,研究区内地质灾害多分布于海拔300m~600m 处的低山丘陵地带。
坡度与地质灾害发生密切相关,坡度越陡,滑坡体摩擦力越小,滑坡越容易发生,研究区内危险坡度为15°~36°之间。
坡向通过日照时常与蒸发量等因素对地质灾害产生影响;由于地质灾害触发因素主要有降水和地震,因此将降雨量与表征地震的地震动峰值加速度和距离断层距离纳入评价因子,由图可知,研究区降水量自东向西依次增加,与地质灾害点分布相吻合,表明降水量是影响地质灾害的因素之一。
由于受到人为活动干扰,导致部分地区岩石土体松动或者边坡稳定性降低,容易发生滑坡等地质灾害,故表征人类活动的POI 点密度与道路距离纳入评价因子。
河道冲刷会使含水量与坡度等发生变化而导致边坡失稳,进而发生地质灾害,故距河流距离纳入评价因子,距河流越近,地质灾害发生越频繁。
评价因子过多会带来因子冗余,部分因子相关性太强,使得易发性分区精度呈现过饱和的趋势[12]。为此,本文引入Mahalanobis 距离[13],利用频率比作为数值[14],应用步进式方法进行相关性检验。
Mahalanobis 距离表示数据协方差距离,由于其充分考虑了两组数据集间的特征与联系,可以利用其计算两组数据集的相似度,是进行数据相关分析常用方法之一[15]。频率比(FR)表示分级后的评价因子中,各分级对易发性的影响程度[16],其定义如下:

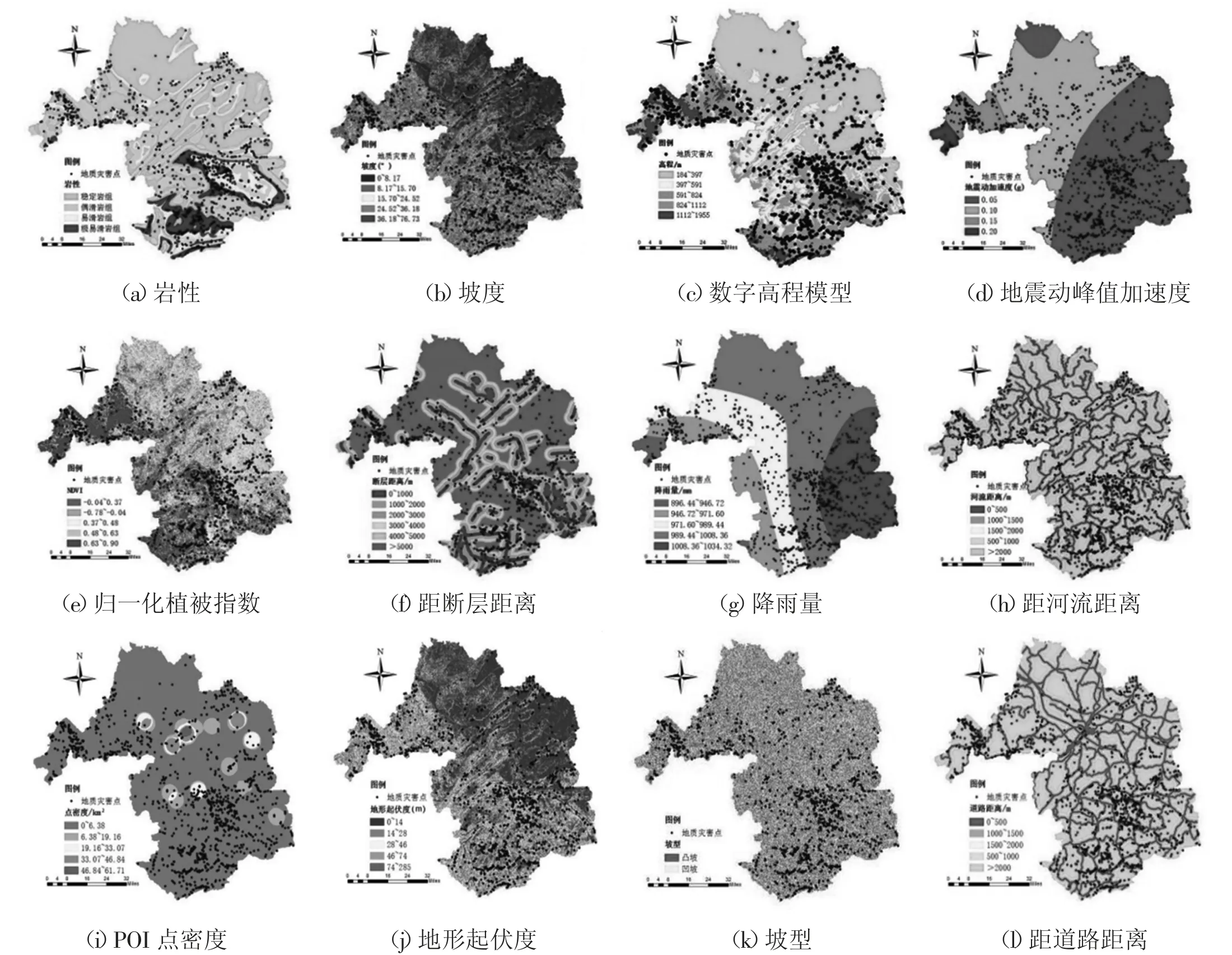
图1 易发性评价因子
其中:N1表示分类内地质灾害栅格数;N2表示分类栅格数;S1表示研究区地质灾害总栅格数;S2表示研究区总栅格数,当FR>0 表示该分类区间有利于地质灾害发生;当FR<0 表示该分类区间不利于地质灾害发生(见表1)。Mahalanobis 距离计算基于SPSS 完成。
经因子相关性分析,最终确定12 类因子(岩性、坡度、DEM、地震动加速度、NDVI、断裂带距离、降雨量、水系距离、POI 点密度、地形起伏度、坡型、道路距离)显著性小于0.05,即该12 类因子无相关性,可以进行模型构建(见图1)。
3 信息量与Logistics 耦合模型
3.1 信息量模型
信息量模型是信息理论延伸出的预测模型,理论基础是将地质灾害各影响因子单独进行分析。将各因子分级后,各分级状态对地质灾害易发性影响程度不同,影响程度即为信息量,信息量数值可以表示地质灾害与影响因子之间的关系[17-18]。
总信息量为:
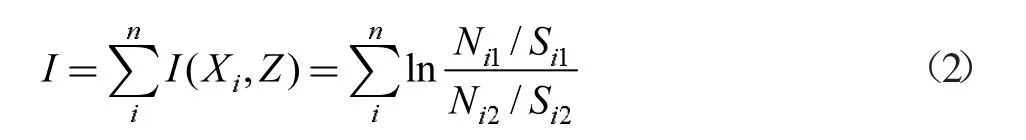
其中,I(Xi,Z)是评价因子Xi(i=1,2,3...)的信息量,其中:N1表示分类内地质灾害栅格数;N2表示分类栅格数;S1表示研究区地质灾害总栅格数。
信息量值如表1 所示。
3.2 Logistic 模型
Logistic 模型主要应用于医学领域,属于线性回归的一种。其对结果进行二分类,一般结果可用1 和0 代表发生与未发生,由于Logistic 模型对评价因子包容性好,即评价因子可以是连续型变量也可以是非连续型变量且客观公正,目前广泛应用于易发性分区中[14]。但Logistic 模型计算繁琐,进行易发性分区精度不如信息量模型等缺陷也制约其在易发性分区中大规模应用。计算公式为:
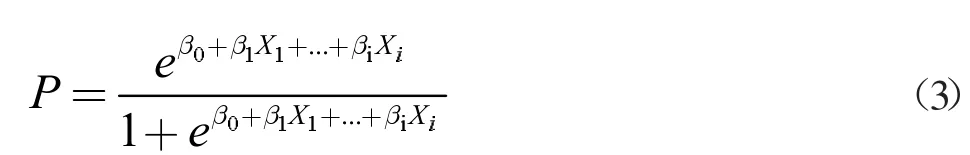
其中P 为结果发生的概率,β0为常数项,βi为非常数项系数,使用频率比,基于SPSS 计算Logistic 模型系数,计算结果见表2。

表1 信息量表

表2 Logistic 模型计算表
3.3 信息量与Logistic 耦合模型
针对信息量模型忽略各评价因子对地质灾害易发性贡献率不同的缺陷,采用Logistic 模型系数作为信息量法权重,在ArcGIS 中使用栅格计算器进行图层计算。
由于使用的Logistic 模型系数是不依赖主观评判,所以该耦合模型既避免AHP 法主观定权的缺陷,又保留信息量法精度高、简单易行、运算速度快的优势,同时避免Logistic 模型计算繁琐、精度较低的弊端。计算公式为:

4 易发性评价结果及精度检验
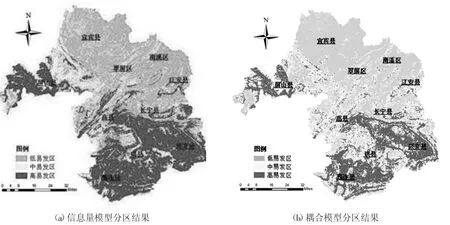
图2 宜宾市地质灾害易发性分区
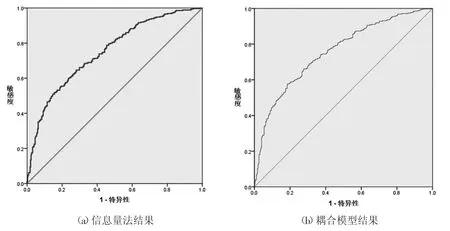
图3 ROC 曲线
4.1 易发性评价结果
将上述12 类评价因子进行叠加分析,利用自然断点法将研究区分为三类,分别为低易发区、中易发区和高易发区(见图2)
从图2 可知,屏山县、筠连县、兴文县地质灾害发生频繁,宜宾县、翠屏区、南溪区等地质灾害发生率低。结合DEM、坡度、岩性等信息可知,高易发区大多位于山区且坡度较陡处,岩性以粉砂岩或者泥岩为主的地区。
信息量模型计算得到的高易发区多于耦合模型得到的高易发区;但两个模型易发区走势基本一致,初步证明分区结果准确。
4.2 精度检验
本文应用ROC 曲线计算AUC 值进行精度验证。ROC 曲线又称为受试者特性曲线,是医学上常用的关联性分析方法,其通过设定阈值来表达观测量与结果的关联度,关联度越高,表明观测值与发生结果越紧密,其精度也越高。AUC 值为ROC 曲线下方与坐标轴构成的面积,对ROC 曲线进行积分运算,值越大表明拟合度越高。由于其简单便捷,也常常被用来进行易发性分区制图精度的检验[19]。本文综合前人经验[19]设定阈值为0.5,通过验证组数据进行验证,经计算,信息量模型AUC 值为0.749,信息量-Logistics 耦合模型AUC 值为0.756,结果表明耦合模型精度更高(如图3)。
5 结果
本文通过信息量模型与Logistics 模型进行耦合,利用Logistics 模型系数表示各评价因子重要程度为信息量模型赋予权重,改进了信息量模型忽略评价因子对易发性贡献率不同的弊端,提高了易发性分区结果的精度。经计算,信息量模型精度为74.9%,信息量-Logistics 耦合模型精度为75.6%,结果表明耦合模型精度更高,该方法简单易行,不受人为因素干扰,既保留信息量法计算速度快,原理简单的优势,又避免Logistics 模型精度较低,计算繁琐的弊端,客观公正,可以作为易发性分区的模型。
