基于解耦的工程振动控制
2021-03-15陆新征
黄 伟, 徐 建, 陆新征
(1.国机集团科学技术研究院有限公司 国机集团工程振动控制技术研究中心,北京 100050; 2.清华大学 土木水利学院,北京 100084; 3.北京起重运输机械设计研究院,北京 100007; 4.中国机械工业集团有限公司,北京 100080)
0 引 言
工程振动控制中,应尽可能降低因自由度耦合带来的不利效应,如通过降低质心使隔振体系接近非耦合状态[1-3]。对于线弹性隔振体系,其固有频率随负载质量变化,体系设计完成后,其隔振特性固定,且在实际工程中,很难控制到2 Hz以下的低频。双腔室空气弹簧有效地解决了固有频率随负载耦合的难题,并可实现低频控制。
本文研究了体系解耦、与负载解耦问题以及被、主动一体的混合控制方法。
1 质刚重合的体系解耦
隔振器在隔振平台中的位置有2种:① 隔振器位于平台下部(质刚不重合);② 隔振器嵌入隔振平台中部,即质心与提供外界刚度的隔振器作用力位于同一平面(质刚重合)。2种质刚相对位置形态的隔振平台如图1所示。
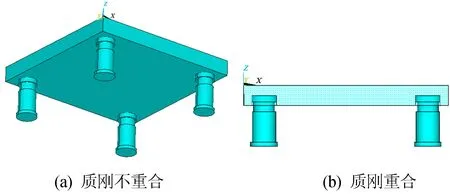
图1 2种质刚相对位置形态的隔振平台
本文研究质刚重合隔振体系,隔振平台为大理石基台,尺寸为2 m×2 m×0.2 m,隔振器为钢弹簧,忽略体系非线性和阻尼影响,隔振体系竖向设计频率为3.5 Hz,频率范围为1~10 Hz,沿x、y、z方向施加的全局加速度均为1 m/s2。隔振体系解耦与非解耦状态下的谐响应对比如图2所示。
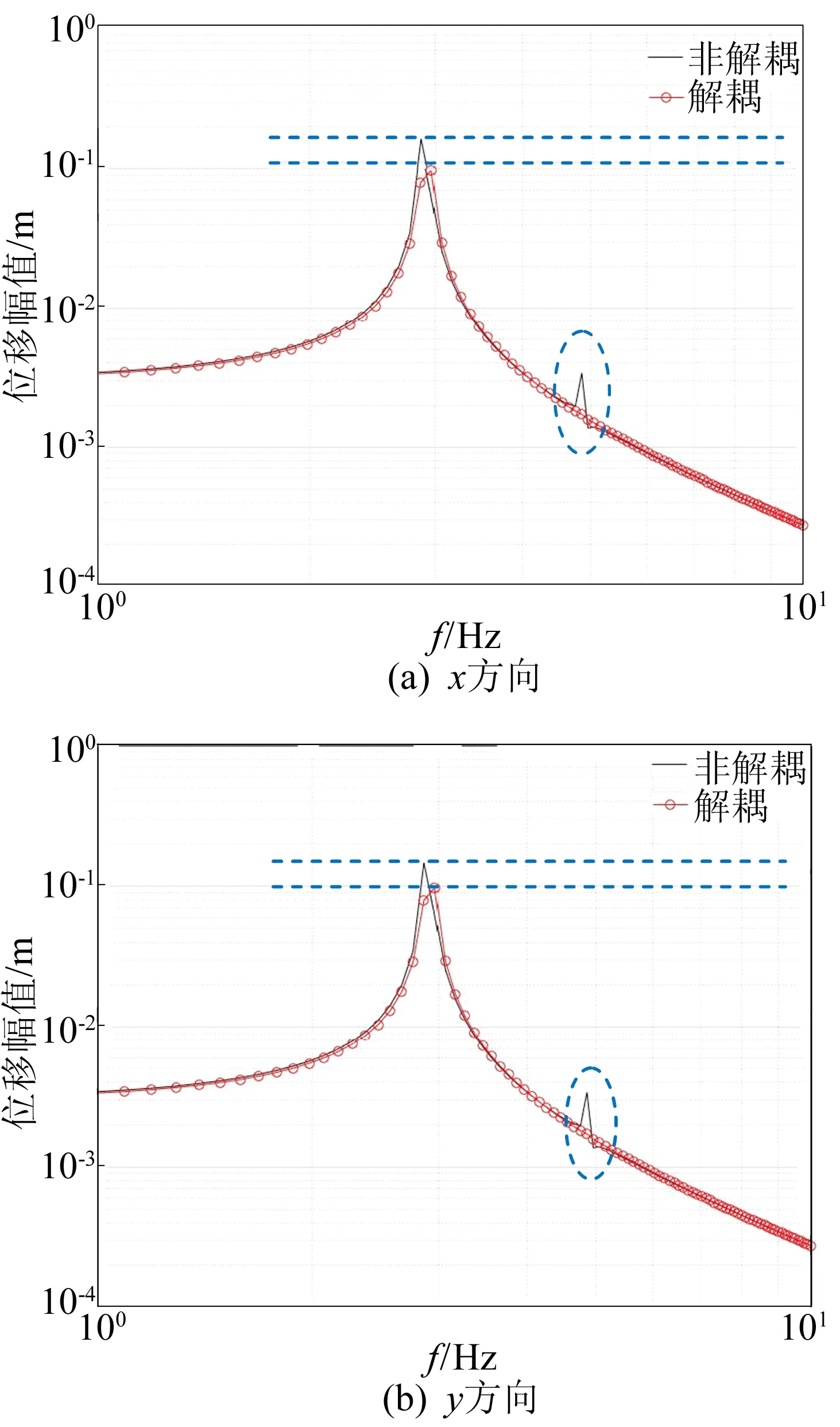
图2 隔振体系解耦与非解耦状态下的谐响应对比
从图2可以看出,解耦状态下的x、y向谐响应峰值比非解耦状态有所减小,z向谐响应在共振峰前明显小于非解耦状态,且解耦体系可避免因自由度耦合带来的除主共振峰外的其他易共振点发生。在实际工程中,应尽量使体系实现质刚重合,使体系接近非耦合。
2 固有频率与负载解耦
对于线性隔振体系,其固有频率随负载质量的增加而降低,对于以低频为主的微振动控制,需要设计较低固有频率,此时体系将变得很柔,变形很大,很难在实际工程中应用。为此,可以采用空气弹簧气浮式振动控制系统,来解决低频控制难题,而双腔室空气弹簧[4]的设计,可以有效解决隔振器固有频率与负载解耦的问题。双腔室空气弹簧示意图如图3所示。
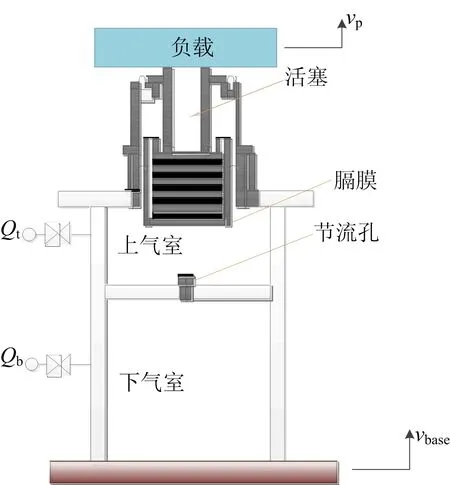
图3 双腔室空气弹簧示意图
双腔室空气弹簧的动力学模型[4]为:
(1)
(2)
(3)
其中:Pt为上腔室空气压强;Pb为下腔室空气压强;vp为负载振动速度;vbase为作用在空气弹簧底部的速度激励;Qt为上腔室空气流量;Qb为下腔室空气流量;Fd为外界干扰力;n为多变指数;R为通用气体常数;T为绝对温度;ρ为空气密度;Cr为流阻常数;Vt0为上腔室初始体积;Ap为活塞有效面积;P0为上下腔室初始压强;Vb为下腔室初始体积;mp为负载质量。
下面给出双腔室空气弹簧隔振系统的传递函数。基底激励下的传递函数为:
(4)
作用在负载上的力激励下的传递函数为:
(5)
其中:s为拉普拉斯算子;xp为负载振动位移;xbase为作用在空气弹簧底部的位移激励。
空气弹簧参数取值如下:节流孔直径d=6.1×10-4m,节流孔长度l=7.27×10-3m,mp=110 kg,n=1.4,Ap=1.85×10-3m2,Cr=2.85×10-8m3/(s·Pa),Patm=101 325 Pa,R=286.9 Pa·m3/(kg·K),T=298 K,Vb=4.18×10-4m3,Vt0=7.32×10-5m3,空气黏度系数μ=1.824×10-5Pa·s,膈膜刚度kd=8 170 N/m,膈膜黏滞阻尼系数cd=60 N·s/m,膈膜滞回阻尼系数hd=0。
双腔室空气弹簧传递率计算曲线如图4所示。经计算该双腔室空气弹簧固有频率为0.9 Hz。
双腔室空气弹簧固有频率的简便计算公式[5]为:
(6)
其中:ωn为固有频率;g为重力加速度;γ为空气的质量热容比,γ=1.4;h为腔室有效高度。
当h不变时,其ωn不变,即与负载质量大小无关。
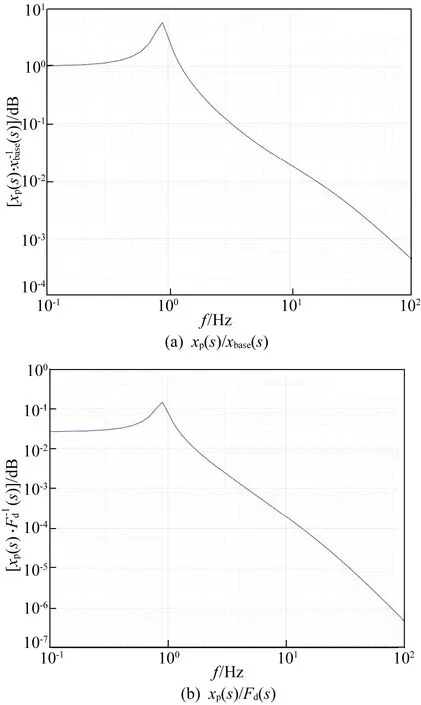
图4 双腔室空气弹簧传递率计算曲线
由上述分析可知,(6)式可以为双腔室空气弹簧设计提供依据,其ωn计算简便;由双腔室空气弹簧的动力学模型得到的空气弹簧传递率计算曲线可与空气弹簧实际试验曲线相互验证,两者结合可实现空气弹簧特性的不断优化。
3 与负载解耦的被、主动混合控制
在与负载解耦的气浮式振动控制体系基础上,本文引入“传感-控制-作动”系统,开展被、主动混合控制研究。
令状态变量δPt=x1,δPb=x2,δVp=x3,则(1)~(3)式变为如下形式:
(7)
(8)
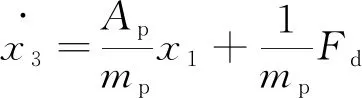
(9)
再将(7)~(9)式变为如下状态方程形式:
(10)
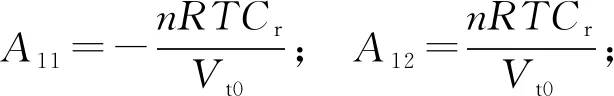
ρ=Pt/(RT),为时变量;Pt=P0+δPt,为时变量。
在全状态观测输出下,有
(11)
将(10)式和(11)式合并,有
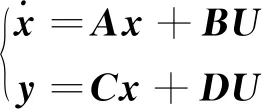
(12)
其中
当考虑膈膜动力效应时,双腔室空气弹簧的动力学模型如图5所示。
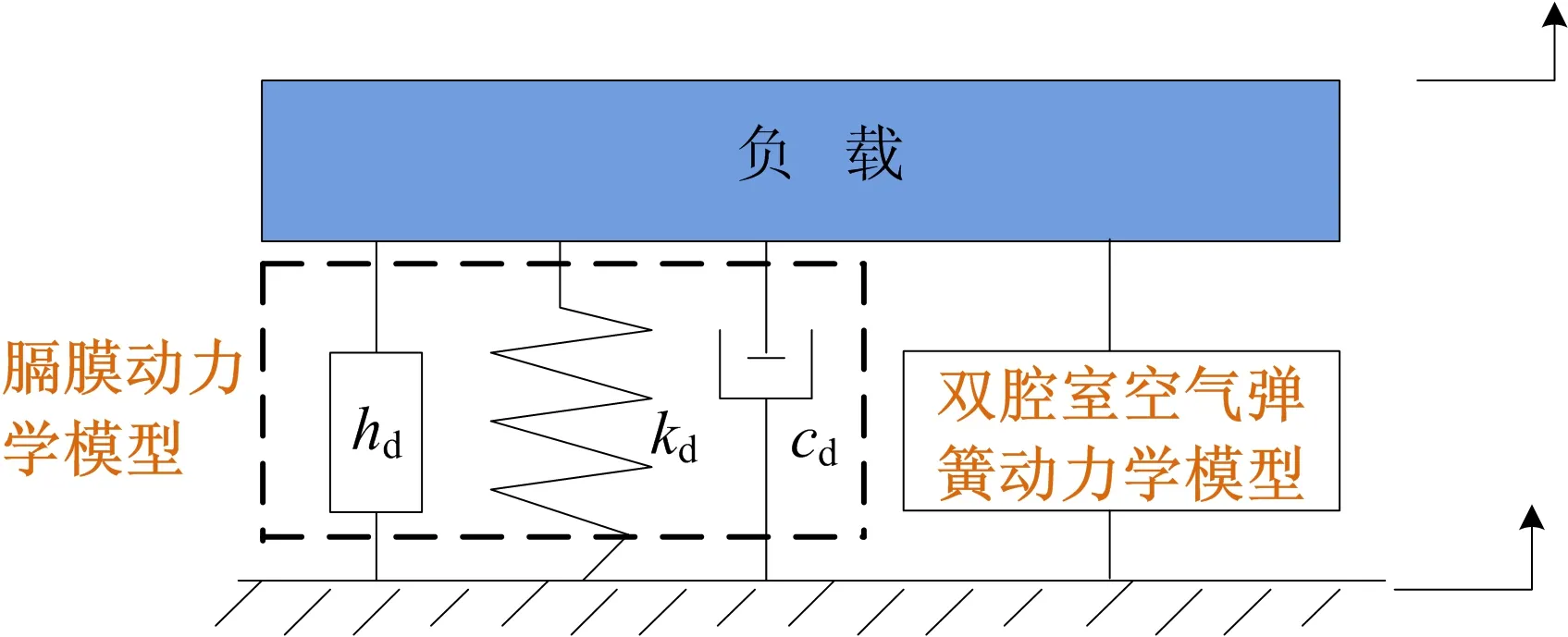
图5 考虑膈膜效应的空气弹簧模型
当体系引入主动控制时,即存在作用在负载上的主动控制力Fa,可以抵消外界振动荷载,此时(9)式变为:
(13)
主动控制采用比例-积分-微分(proportional-integral-differential, PID)控制,其比例、积分、微分控制因子可通过经典理论进行整定,也可通过粒子群优化(particle swarm optimization, PSO)算法、遗传算法(genetic algorithm,GA)等进行寻优[6-7],本文分别取为-500、-500、-500。
考虑外界振动荷载分别为:① 作用在负载上的Fd,其为幅值为1 N的随机白噪声荷载;② 作用在空气弹簧底部的位移激励xbase、速度激励vbase,其为幅值分别为1×10-6m、1×10-6m/s的随机白噪声荷载。
引入主动控制后的模型如图6所示,此时体系为被、主动一体的混合控制。有、无主动控制体系的响应对比如图7所示。
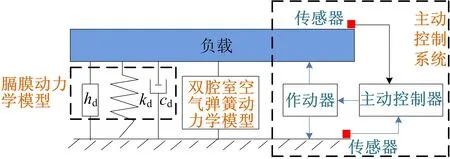
图6 被、主动混合控制
从图7可以看出,混合控制可以明显改进被动控制效果。作动器出力如图8所示。事实上,进一步提升主动控制效果、作动器出力范围,体系的响应可以继续改善,但在实际工程中应兼顾经济性,单纯追求控制效果是没有必要的。
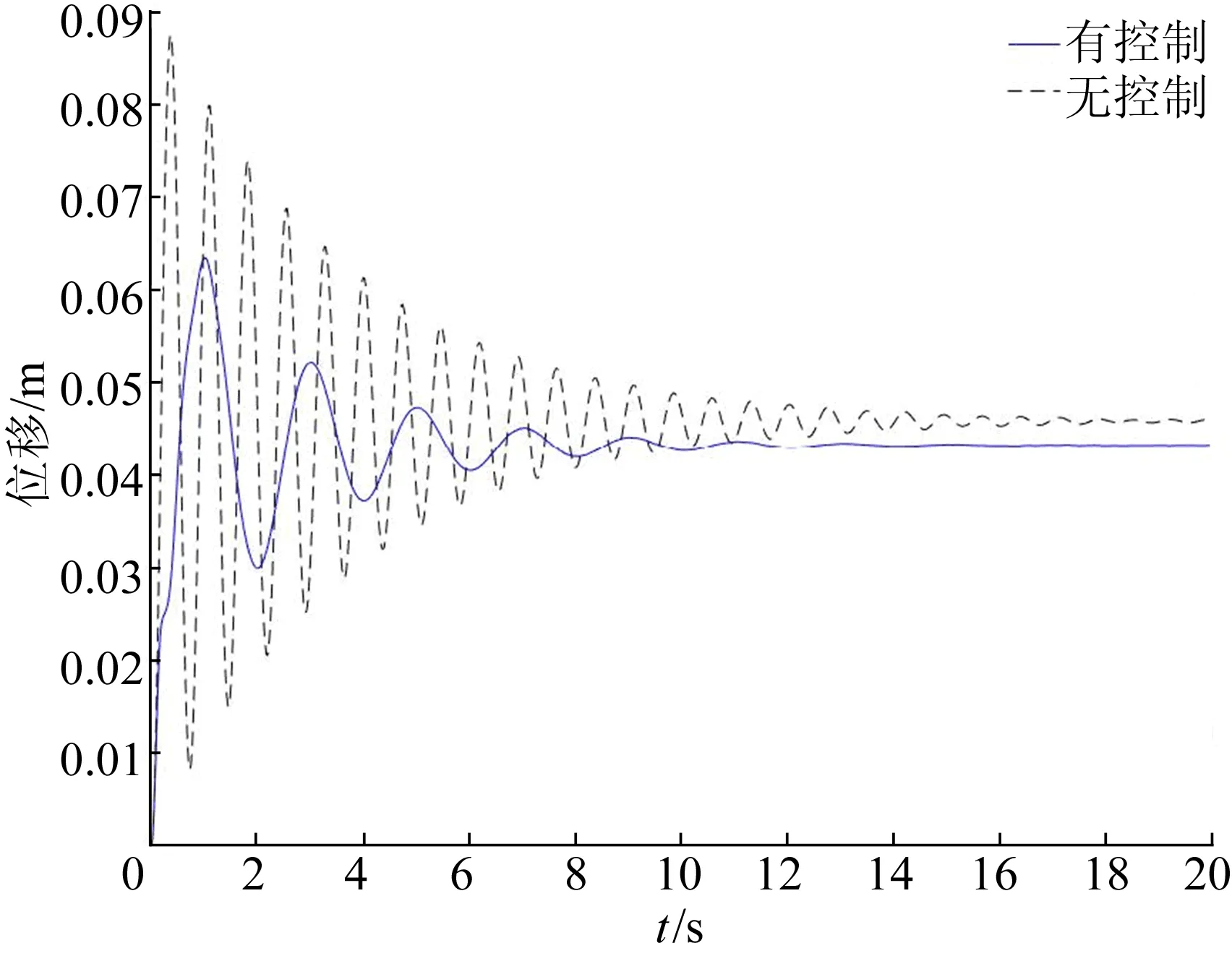
图7 有、无主动控制体系响应对比
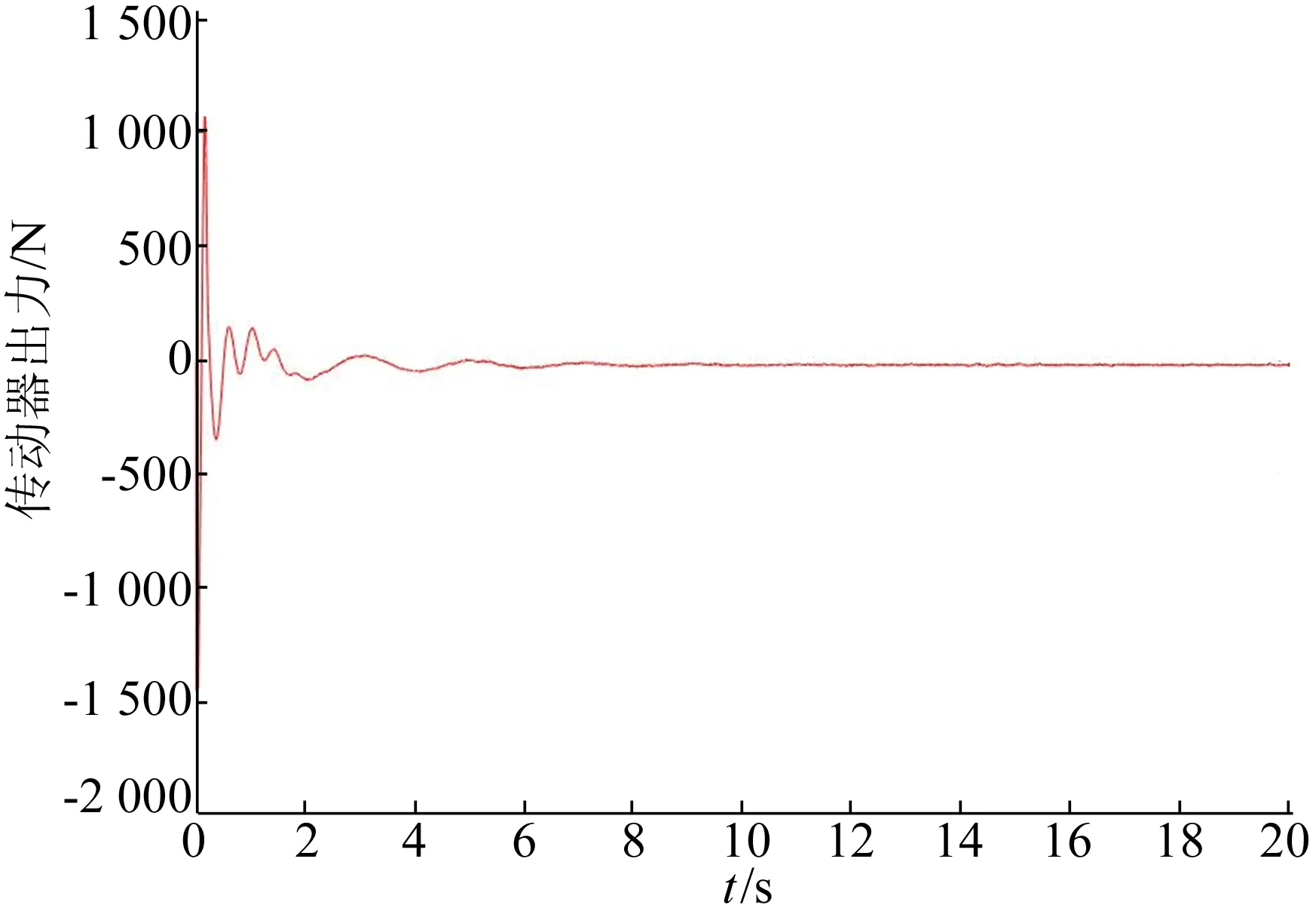
图8 主动控制的作动器出力
4 结 论
本文针对基于质刚重合的体系解耦进行研究,结果表明解耦可以明显克服非解耦造成的不利效应;对可以实现低频及固有频率与负载解耦的双腔室空气弹簧进行了动力学分析,并在此基础上,研究了基于负载解耦的被、主动混合控制方法,结果表明混合控制可以明显改善被动控制的效果。
在实际工业工程中,对于动力装备振动控制,多是基于线性钢弹簧,需要尽可能实现体系解耦;对于精密装备振动控制,多是基于空气弹簧的气浮体系,需要在体系解耦的基础上,尽可能实现与负载解耦,当被动控制的效果无法满足时,需要采取被、主动一体的混合控制,被动体系用于支撑被隔对象,主动体系用于实时提供控制力,以抵消外界扰动。本文研究对工业工程振动控制具有一定的实际意义。
