一种改进SIFT的SAR与可见光图像配准算法

2021-03-15石聪聪杨学志董张玉王守峰

合肥工业大学学报（自然科学版） 2021年2期

石聪聪, 杨学志, 董张玉, 王守峰

(1.合肥工业大学计算机与信息学院,安徽合肥 230601; 2.工业安全与应急技术安徽省重点实验室,安徽合肥 230601)

随着高分辨率遥感卫星对地观测研究的逐步推进,积累的多源遥感数据数量在不断增加,而遥感图像配准是实现图像融合、变化检测、图像镶嵌和目标识别等的前期准备工作,于是对遥感图像配准的需求大大增加,尤其对于多源遥感卫星图像的配准研究尤为重要。在多源遥感图像配准研究中,合成孔径雷达(synthetic aperture radar,SAR)图像具有穿透性强、全天候、纹理信息丰富等优点,但其缺乏光谱信息,且目标的微波反射特性导致相同物体的SAR图像可能呈现不同的表现形式。而可见光图像富含丰富的光谱信息,目视效果较好,但易受到大气状况影响,特别在阴雨天气时会被云层遮挡导致成像质量较差[1-3]。根据上述SAR图像与可见光图像的优劣势,开展SAR图像与可见光图像的配准研究有着重大意义。

现有遥感图像配准方法基本分为基于区域灰度信息配准与基于特征信息配准两类。其中,基于区域灰度信息配准算法主要包括:互相关法、互信息法与序列相似度检测算法等[4]。因为基于区域灰度信息配准算法对灰度变化比较敏感,尤其针对非线性光照变化,将大大降低算法性能,并且计算复杂度较高,抗旋转性与抗形变性较差[5],所以在SAR图像与可见光图像配准研究中较少采用。基于特征信息配准算法中较为常用的算法是文献[6]提出的尺度不变特征变换算法(scale invariant feature transform,SIFT)。SIFT算法具有尺度不变性、旋转与仿射不变性,并且对于噪声也有一定的鲁棒性，但在SAR图像与可见光图像配准中表现不佳,主要原因是SAR图像存在较多的乘性相干斑噪声,导致SAR图像提取到的特征点质量较差无法达到匹配要求。文献[7]提出一种基于相位一致性与非线性扩散的改进SIFT算法来抑制SAR图像的斑点噪声。文献[8]提出一种将Harris算子与指数加权平均值(ratio of exponentially weighted averages,ROEWA)结合的改进SIFT算法来提高SAR图像特征点的稳定性。文献[9]提出基于非下采样contourlet变换(non-subsampled contourlet transform,NSCT)与SIFT相结合的遥感图像配准算法,通过NSCT算法提高算法速度。文献[10]提出基于非下采样Shearlet变换(non subsampled shearlet transform,NSST)和加速分割检测特征(features from accelerated segment test,FAST)结合的配准算法,从而解决图像配准速度较慢的问题,但只注重了速度提升,提取特征点数量与质量都不够高,准确率低于传统SIFT算法,并且只针对同源图像配准,异源图像尤其SAR与可见光图像配准效果不佳。

针对上述问题,本文提出一种基于NSST与改进SIFT算法相结合的SAR图像与可见光图像配准算法。首先,为了有效去除SAR图像的乘性相干斑噪声,本文采用目前针对SAR图像滤波效果较好的PPB(probabilistic patch-based)算法[11],在滤除相干斑噪声的同时保持图像边缘信息。然后通过NSST变换提取SAR图像与可见光图像的低频信息图像。之后对可见光图像低频图像采用SIFT算法提取特征点,对SAR图像低频信息图像采用Harris 算子和 ROEWA 边缘检测算法相结合提取特征点,通过快速近似最近邻搜索(fast library for approximate nearest neighbors algorithm,FLANN)算法对SAR图像与可见光图像特征点描述子进行粗匹配得到初始匹配点。最后,采用改进的随机抽样一致算法(random sampling consensus algorithm,RANSAC)算法剔除初始匹配结果中的误匹配点,进一步提升匹配的准确率与速度。

1 本文算法

1.1 PPB滤波

PPB是一种空域滤波方法,该算法在最大似然估计的框架下得到加权平均公式,并定义块权值的计算公式,通过迭代方法逐步修改先验信息,最终收敛至最佳去斑结果[12]。

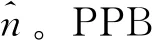
(1)

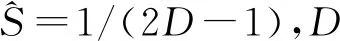
PPB滤波是通过概率论推导给出了任意噪声分布下的最优图块相似性度量,因此可以在去除加性噪声与乘性噪声的同时有效保持边缘特性。本文选择PPB滤波可以在SAR图像进行SIFT提取特征点前有效去除相干斑噪声的影响,从而提高特征点提取的数量与质量。

1.2 NSST变换提取图像低频信息

NSST变换是非正交变换[13],离散化过程主要分为:基于非下采样金字塔滤波(non-subsampled pyramid,NSP)的多尺度分解和基于改进的剪切波滤波(shear filter,SF)多方向分解[14]。

多尺度分解通过进行NSP得到低、高频系数分量,之后每层进行NSP都是在上一层次的低频中进行迭代操作,以得到图像中的奇异点,之后进行k次反复分解,最终形成大小为1个低频和k个高频,形成的高低频分量大小相同。

多方向分解运用标准的SF器,将伪极化网格系统对应到笛卡尔坐标系统上,之后再经过傅里叶变换实现二维卷积步骤,以此避免标准SF器存在的下采样步骤,达到平移不变目的。具体操作实现过程为:

(1) 将伪极化网络系统映射到笛卡尔坐标上。

(2) 采用“Meyer”构建窗函数,形成SF器。

(3) 将k个高频子图像和“Meyer”构建的窗函数进行卷积,然后获取方向子图像。

NSST离散化过程如图1所示。

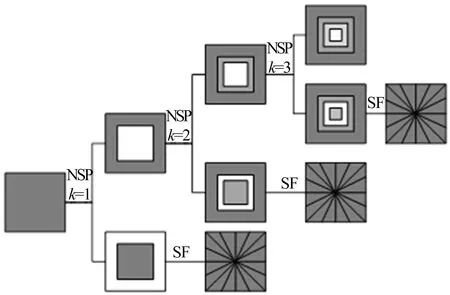
图1 NSST离散化过程图

与NSCT不同的是,NSST采用笛卡尔坐标系统,直接运用逆傅里叶变换完成二维卷积操作,避免了下采样的环节,故NSST平移不变性更强[15]。本文采用NSST提取低频信息。

1.3 SIFT特征检测和描述1.3.1 传统SIFT特征点检测算法

传统SIFT算法步骤为:

(1) 尺度空间极值检测。搜索所有尺度上的图像位置，通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

(2) 关键点定位。在每个候选的位置上,通过一个拟合精细的模型来确定位置和尺度，关键点的选择依据于它们的稳定程度。

(3) 方向确定。用直方图统计邻域像素的梯度方向,直方图峰值即为该关键点的主方向。将坐标轴旋转为特征点的主方向,以确保旋转不变性。

(4) 关键点描述。在关键点邻域划分成的小区域内计算梯度方向和模值,生成梯度方向直方图,由各个小区域梯度方向直方图建立关键点的特征向量,即为描述子。

差分高斯尺度图像的像极值检测如图2所示。

图2 尺度空间极值点检测示意图

利用特征点邻域内所有像素点的梯度方向分布特性为特征点指定方向,使特征点具有旋转不变性。其中:LX=L(x+1,y)-L(x-1,y);Ly=L(x,y+1)-L(x,y-1),那么

(2)

(3)

(2)式、(3)式分别为相应点的梯度模值和梯度方向,L为关键点所在的尺度空间值。

1.3.2 改进SIFT特征点检测算法

由于SAR图像存在乘性噪声,SAR图像在拥有高反射率区域获取幅值很大的梯度时,传统SIFT在提取梯度时会出现一定的偏差,影响后续特征点匹配。针对上述问题改进的SIFT算法[8]提出了新的梯度算法,使梯度幅值和方向对斑点噪声有较好的鲁棒性。因此,本文参考该算法提取SAR与可见光图像特征点,用于后续匹配特征点匹配。

本文采用Harris 算子和 ROEWA 边缘检测算法相结合的方法提取特征点。具体步骤为:

(1) 比例算子计算梯度。给定图像中任一像素点M(a,b),使用对多尺度边缘信息更加精确的指数加权平均算子,得到像素M点一定范围内像素点幅度值的指数加权均值,即

(4)

(5)

其中:H为图像;γ为指数加权的系数,作用相当于传统SIFT算法中的尺度因子；R、R+、R-为指数加权函数在该方向上的积分范围。Y方向上的Fy+与Fy-(4)式、(5)式,只需将积分范围从x轴换至y轴。像素点M(a,b)沿水平方向梯度Gx,γ=log(Fx+/Fx-),沿垂直方向梯度Gy,γ=log(Fy+/Fx-)。

像素点M(a,b)的梯度幅值和梯度方向分别为:

(6)

θγ=arctan(Gy,γ/Gx,γ)

(7)

(2) 建立多尺度SAR-Harris空间。根据求得的梯度按照SAR-Harris尺度空间表达式构建尺度空间,表达式为:

(8)

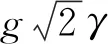
(3) 在多尺度SAR-Harris空间中检测极值点。与传统SIFT相同,对于构建好的SAR-Harris尺度空间,极值点的判定规则仍为与邻域内26个邻域点做比较,判断该点是否为最值。在关键点邻域划分成的小区域内计算梯度方向和模值,生成梯度方向直方图,由各个小区域梯度方向直方图建立关键点的特征向量,即为描述子。

1.3.3FLANN算法

传统SIFT算法在特征点匹配时采用的是基于最近邻距离匹配算法,对于128维高维特征点描述子,算法复杂度较高,计算量繁重。本文为提高匹配的效率与速度,并保证匹配的精度,引入FLANN算法[16]，利用FLANN算法对特征点间的欧式距离进行特征点初始匹配。

FLANN模型的特征空间通常是一个n维的实向量空间，命名为Rn,其核心是寻找基于欧氏距离的相邻点。特征点m和n的子向量分别用Sm和Sn表示,则D(m,n)的欧氏距离如下式:

D(m,n)=〈Sm-Sn·Sn-Sm〉

(9)

Rn中的所有D(m,n)都存储在若干个基于KD(k-dimensional)树部分的结构中。在整个KD树中搜索到接近查询点的最小欧式距离,从而有效地搜索到参考点的最近点,最后得到特征点初始匹配点集。

1.3.4 改进的RANSAC样一致算法

为了进一步提高匹配效率,本文采用RANSAC剔除初始匹配点对中的误匹配。传统RANSAC[17]算法充分利用所有的初始匹配点对,根据一个配准允许的误差将匹配点对分隔为内点与外点,然后利用内点数据的一致性特点来进行参数估计。但是,如果直接使用RANSAC进行估计,运行效率很低,因此本文改进RANSAC算法来剔除误匹配点,在传统RANSAC基础上,将初始匹配点集根据匹配结果质量由高到低进行排序,并根据特征点初始匹配结果选取参与RANSAC抽样的点集。计算初始匹配点集的均值与方差,根据离散程度,调整参与后续RANSAC计算的样本。将匹配度最高的初始匹配点优先采样,这样使得最有可能的最佳匹配参数较早地产生。步骤如下:

(1) 对匹配点对的欧式距离点集进行排序。

(2) 从最高品质方程数据集抽取假定的采样。

(3) 根据从小到大的顺序依次在所有数据点上验证假设。

结束条件是当最优解概率小于设定阈值U时结束,一般U设定为5%。

1.3.5 本文算法步骤

为了得到较多的特征点与匹配点,本文提出了一种有效的SAR图像与可见光图像配准算法,其具体实现步骤如下:

(1) 输入可见光图像与SAR图像。

(2) 对SAR图像进行PPB滤波。

(3) 对可见光图像与SAR图像进行NSST变换。

(4) 对低频图像通过改进的SIFT提取特征点。

(5) 利用FLANN算法匹配特征点。

(6) 采用改进的RANSAC算法剔除误匹配点对。

算法流程如图3所示。

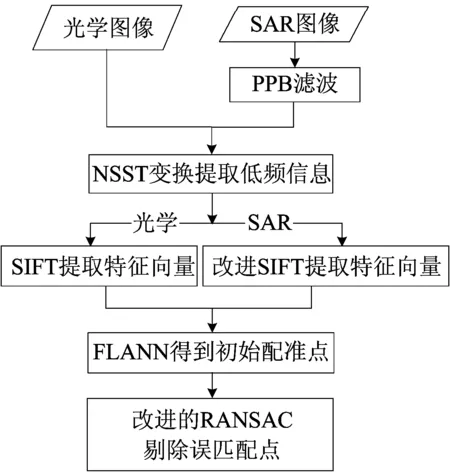
图3 本文算法框架图

2 实验结果与分析

本文通过2组SAR图像和可见光图像的配准实验对提出的算法进行精度和速度的评价,并与传统SIFT算法和文献[10]算法作对比。

实验数据截取于2018年8月份安徽省淮河段遥感图像。实验数据如下:SAR图像采用国产高分三号全极化条带2(FSII)成像模式的雷达卫星图像,分辨率为10 m;光学图像采用国家高分一号全色图像,分辨率为2 m。匹配结果如图4、图5所示。

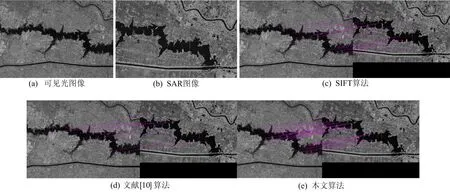
图4 第1组配准结果

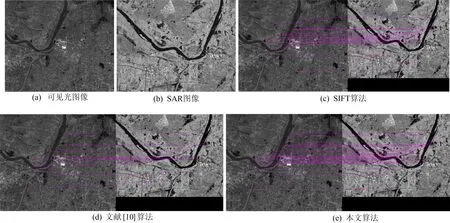
图5 第2组配准结果

评价结果见表1所列,本文获取的SAR图像特征点是最多的,正确配准率相比SIFT算法与文献[10]算法均有较大的提升。速度相比文献[10]略慢是因为SIFT算法相比于FAST算法复杂度较高,运算时间较长,但本文算法速度相比于传统SIFT算法提升2倍以上,原因是NSST提取低频信息,降低了后续运算的数据量,并且本文采用FLANN算法与改进的RANSAC算法,大大提升了匹配的运算效率。第1组实验中,传统SIFT算法正确率为76%,文献[10]算法正确率为66%,本文算法正确率是86%;第2组实验中,传统SIFT算法正确率为72%,文献[10]算法正确率为63%,本文算法正确率为88%;针对两组实验数据本文算法相比于传统SIFT算法正确率均提升10%以上。正确率提高的原因是改进的SIFT算法有效地滤除了相干斑噪声的影响,提取到的SAR图像特征点有较强的鲁棒性,从而保证了配准的精度。