三角形中线再认识
2021-03-15文余
文余 芳
(作者单位:江苏省无锡市西漳中学)
一、三角形中线再认识
例1三角形的下列线段中能将三角形的面积分成相等的两部分的是( )。
A.中线 B.角平分线
C.高 D.中位线
【解析】如图1,AD是△ABC的中线,根据三角形中线的定义我们可以得到BD=CD,进而得到S△ABD=S△ADC=S△ABC(等底同高)。故选A。

图1
二、三角形中线性质的应用
例2如图2,在△ABC中,将△ABC沿射线BC方向平移,使点B移动到点C,得到△DCF,连接AF,若△ABC的面积为4,则△ACF的面积为 。
【解析】通过平移,我们可以得到BC=CF,从而发现AC是△ABF的中线,考查的还是三角形中线的性质,S△ACF=S△ABC=4。故填4。
例3如图3,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,则△BEF的面积是______cm2。
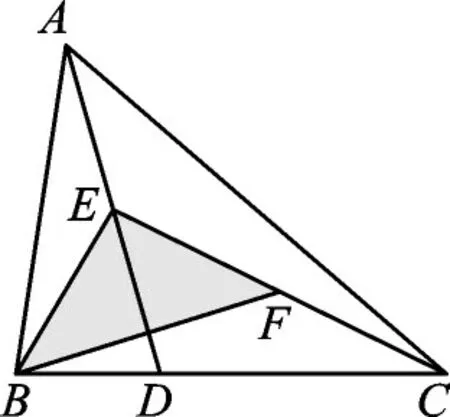
图3
【解析】审题找到解题突破信息:E、F分别是线段AD、CE的中点,遵循点—线—图形的发现轨迹,从而发现BE是△ABD的中线,CE是△ADC的中线,BF是△BCE的中线,题目所求又与三角形面积有关,所以我们自然想到三角形中线平分面积的性质。
解:∵E是AD的中点,

∵F是CE的中点,
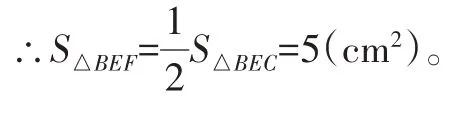
三、三角形中线性质的拓展
例4如图4,在△ABC中E是BC上一点,EC=2BE,点D是AC的中点,BD与AE交点于F,设△ABC、△ADF、△BEF的面积分别为S△ABC、S△ADF、S△BEF,且S△ABC=12,则S△ADF-S△BEF=( )。

图4
A.1 B.2 C.3 D.4
【解析】我们知道三角形中线平分面积是因为被中线分得的两个三角形是等底同高,由此拓展就可以得到:同高的两个三角形的面积之比等于其底之比。审题后,我们第一直觉是想把S△ADF和S△BEF的面积求出来,但发现能利用点D是AC的中点求得S△ABD=S△BCD=6,再利用EC=2BE可得
距题目所求还有距离。此时我们需要做的是再次审题,把已经求得的和图形特点相结合,发现S△ADF和S△BEF的面积同时加上四边形CEFD的面积就成了△ACE和△BCD的 面 积,即S△ADF-S△BEF=S△ACES△BCD=8-6=2。故选B。
同学们,三角形的中线平分三角形面积是一个重要的性质,其拓展后的一般结论是“同高的两个三角形的面积之比等于其底边之比”,这往往也是中考命题的原型,值得深入理解和掌握。
