基于稳态电流波形匹配的非侵入式家用负荷快速识别方法研究

王建元，侯广铸，张洪明

(1.东北电力大学，吉林 吉林 132012；2.国网吉林省电力有限公司营销服务中心，长春 130062)

能源短缺和全球变暖推动了节能减排技术的创新和实施。电能将逐渐成为现代社会能源使用的主要形式，因此对于电能能耗的详细准确了解对提高用能效率、节能减排起到了至关重要的作用。随着智能电网技术的迅速发展，逐渐形成了基于智能电表的电力负荷监测系统，该系统可以通过实时监测电力网络中每个用电设备的功耗来帮助电力客户管理能量消耗[1]。传统的侵入式负荷监测是在每个用电设备上都要配置数据采集传感装置(智能插头)，尽管该系统可以通过智能插头执行高精度监控，为每个设备提供准确的计量信息，但也会导致高昂的硬件安装和维护成本；而非侵入式负荷监测仅需在用户入口处安装一个数据采样器，便可实现对各设备用电数据的实时监测,该方法具有硬件安装成本低廉，对用户干扰小，易于安装维护等优点[2]。

越来越多的研究学者已经开始将各类智能分类算法应用到非侵入式负荷监测(non-intrusive load monitoring，NILM)系统中，并取得了丰硕的研究成果。文献[3]选取负荷功率作为特征值，以工/休日作为分类标准对负荷功率进行聚类分析，并利用遗传优化算法对负荷类型和工作状态进行识别，解决了现有方法缺乏对多工作状态负荷处理的问题。文献[4]选取稳态电流谐波作为特征值，通过构造方程组来建立目标函数，并利用寻优算法求得的最优解来确定对应功率消耗负荷的类型，进一步提高了辨识准确率。文献[5]通过差量特征提取方法选出低功率负荷中差异较大的谐波电流作为特征值，并利用模糊聚类方法对负荷进行识别，克服了在识别低功率负荷时准确率低的缺点。尽管现有的许多国内外研究成果都达到了对负荷的分解与辨识的目的，但往往都存在特征量表征性不强，识别算法收敛性差等诸多问题[6-9]。

在上述研究背景下，本文提出一种基于波形相似度匹配的非侵入式负荷快速识别方法。在互近似熵(cross-approximate entropy，CApEn)原理的基础上引入二值距离矩阵计算方法，将家用负荷稳态电流波形作为特征量，然后计算出待识别的测试电流波形与模板库中的样本波形之间的互近似熵值，通过熵值来进行波形相似度匹配，可达到对家用负荷类型的快速准确识别的目的，并通过采集实测数据进行实验，验证了所提方法的有效性。

1 家用负荷稳态电流波形特征

家庭用户电路往往具有相同的内部结构，在家庭用户中，每个家用负荷之间都是并联运行的关系。由电路的并联原理可知，家庭用户电力入口处的总电流等于每种家用负荷的电流之和，其中每种用电负荷都是独立工作的，互不影响[10]。根据傅里叶分解原理可以将某次测量中单个用电负荷的电流分解为：

i=α1sin(ωt+θ1)+α2sin(2ωt+θ2)+…+

αksin(kωt+θk)

(1)

式中：第一项为基波，其余项为各次谐波；ω为基波角频率；α1，α2，…,αk为基波及各次谐波的幅值；θ1，θ2,…，θk为基波及各次谐波在每次测量时的初相角[11]。

以上3种变量构成了周期量的3要素，即幅值、频率、初相角。

根据家用电器的不同功能和用途可分为：声像电器、照明电器、制冷电器、清洁电器、洗熨电器等。由于家用电器内部结构相差各异，不同家用电器的稳态电流所包含的谐波种类各不相同，故其稳态电流波形特征也不尽相同。家庭用户设备的稳态电流特征主要由设备自身内部结构所决定，根据各种家用电器的内部结构和元器件特性可分为：纯阻性、电动机、整流型3种负荷类型[12]。

根据上述3种类型，本文选取取暖器、微波炉、电冰箱、计算机和电视机作为典型的家用电器进行仿真实验，这5个典型的用电负荷包含了上述3种负荷类型，具有较强的代表性。

2 互近似熵快速算法

2.1 互近似熵

互近似熵理论是一种能够表示两个离散化序列间复杂程度的方法[13]。通常用做分析两个离散化时间序列或两条连续曲线间的相似性，其实质就是通过计算对应的熵值来描述时间序列的复杂程度，进而在时间轴模式上判断两个序列的相似度[14]。互近似熵值越小，则说明两个时间序列或曲线差异性越小，即相似度越高。

互近似熵定义为：

(2)

式中：m为模式维数；r为相似容限；N为样本数量；A和B分别为两个序列在容限r条件下的相似性，分别记作事件A和B；Pi(B|A)为在满足相似容限r条件下的相似概率。在实际工程应用中，相似容限r通常取对比序列协方差的0.2倍，模式维数m通常取2[15]。

具体算法步骤如下。

a.将包含N个采样点的测试波形序列{i(t)}和样本波形序列{j(t)}进行相空间矢量重构，得到m维的矢量Xp和Xq分别为：

Xp=[i(p),…,i(p+m-1)],p=1,…,N-m+1

(3)

Xq=[j(q),…,j(q+m-1)],q=1,…,N-m+1

(4)

式中p和q分别为测试波形序列与样本波形序列的序号。

b.计算矢量Xp与Xq之间的距离，即两个向量对应元素间的最大差值：

(5)

c.根据给定的相似容限r，统计出d(Xp,Xq)小于r的个数Nm,r，并计算出Nm,r与总矢量数量(N-m+1)的比值Cm,r，该值表示m维模式的序列在相似容限r条件下相互近似的概率，即：

Cm,r=Nm,r/(N-m+1)

(6)

d.计算两个时间序列的互相关程度，对得到的Cm,r求对数，并求其对总矢量数量的平均值，表达式为：

(7)

e.当嵌入维度变为(m+1)时，重复a至d的运算过程，得到(m+1)维时的互相关程度数值Tm+1,r。

f.将步骤d和e得到的Tm,r和Tm+1,r取差值，计算得到互近似熵值：

ECAP(m,r)=Tm,r-Tm+1,r

(8)

2.2 互近似熵的快速计算方法

在实际工程中，由于采样点数较多，利用互近似熵法求CApEn值需要计算n次；另外根据互近似熵算法的原理可知，在计算矢量距离d(Xp,Xq)过程中，包含了大量的冗余计算，这会对计算的效率和速度造成很大影响，使算法运算的速度变慢，效率变低，不利于实时运用。

为此，本文改进互近似熵算法。在互近似熵原理的基础上引入二值距离矩阵，用二值距离矩阵D代替原始的矢量距离矩阵d(Xp,Xq)，该方法不需要重复多次计算矢量距离，进而减少了矢量维度改变之后计算距离过程的计算量，大大提高了运算速度。具体计算方法见图1，图中u、v分别为矩阵D的行、列。

图1 互近似熵快速算法

以m=2为例，首先对N点序列，先构造N×N阶二值距离矩阵D：

(9)

式中dij表示矩阵D中的第i行第j列元素。

然后按照行递增的顺序，以图1中斜线方向的组合方式，对矩阵D中的每两行元素进行“与”运算，再把每一行的结果累加后除以总矢量数量(N-m+1)，即可快速地求得C2,r：

(10)

3 家用负荷辨识实现过程

3.1 稳态电流样本波形库建立

本文所建立的家用电器稳态电流样本波形库包含了取暖器、微波炉、电冰箱、计算机和电视机5种负荷。通过一种负荷登记器来对稳态电流数据进行采集，在用电负荷电压值过零点并增大的时刻开始记录其稳态电流波形，采样时间为电流波形的3个周期，将每种用电负荷波形以长度为600的数据形式进行储存，以此作为样本波形来建立负荷稳态电流模板数据库。样本库中的电流波形见图2。

图2 负荷稳态电流波形

3.2 家用负荷识别流程

将利用互近似熵快速算法进行非侵入式家用负荷识别的过程分解，流程图见图3，分解步骤如下。

a.采集数据。在家庭用户的进线入口处安装数据采样装置，对负荷的电流进行监测，当电流波形趋于稳定状态时，触发器动作，进行数据采集。

b.建立稳态电流样本波形数据库。提取各种家用负荷稳态电流波形数据，每个样本波形取自稳态电流的3个周期，组成参考模板波形数据库。

c.将2种波形序列进行标准化。为了避免2种波形的幅值相差较大而影响匹配结果，依次将待识别的测试序列与模板库中的样本序列标准化，即：

(11)

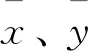
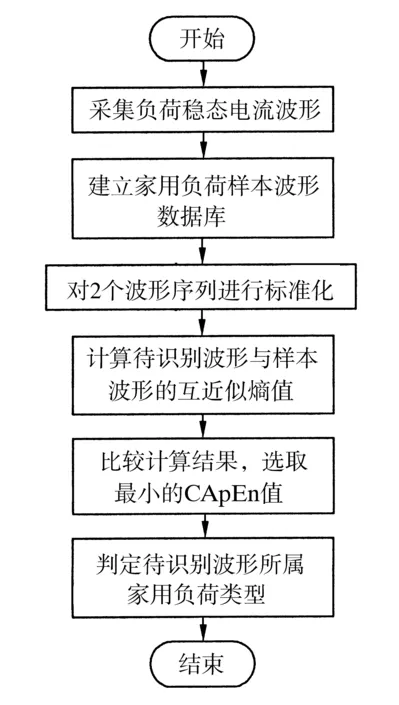
图3 家用负荷识别流程图

d.将待识别的测试波形与样本波形进行匹配。计算出测试波形与样本波形之间的CApEn值。

e.比较匹配后各组的CApEn值。选出其中最小的CApEn值，则可判定测试波形为最小熵值对应的样本波形所属家用负荷类别。

4 仿真实验结果与分析

为了验证本文方法的有效性，通过构建模拟的居民用户网络模型，采集实际负荷的稳态电流信号，利用本文所提算法进行负荷识别。在本次实验中，选取取暖器、微波炉、电冰箱、计算机和电视机作为典型家用负荷以构建用电网络，分别用A，B，C，D，E代表。通过多个时间间隔分别接入不同种类的负荷，形成了包含纯阻性、电动机、整流型等多种负荷类型的多重负荷用电网络。

本文实验中抽取了30组家用负荷测试波形数据，按照算法流程计算出测试波形与5种样本波形之间的CApEn值，再将得到的统计数据做平均化处理，运算结果见表1。

由表1可知，当待识别的测试负荷类型与样本负荷类型相匹配时，计算得到的CApEn值最小，说明这2种负荷电流波形的同步程度最高，即相似度最高，在模式上最接近；当待识别的测试负荷类型与样本负荷类型不一致时，对应的CApEn值较大，明显大于2种波形类型一致时的CApEn值，说明该方法在进行家用负荷识别时具有良好的分类效果，拥有较高区分度。

表1 测试波形与样本波形的平均互近似熵

为了更加直观地理解该方法进行负荷识别时的分类效果，根据以上实验得到的统计数据，做出相互匹配的2种家用负荷间的CApEn值三维效果图见图4。可以看出当2种负荷类型正确匹配时，CApEn值明显小于2种负荷类型不一致时的熵值，图4中表现为对角线部分图形凹陷，明显低于图形其他部分。

图4 互近似熵三维效果图

为了验证利用互近似熵快速算法识别家用负荷的优越性，将本文方法与传统互近似熵和神经网络法比较。使用相同的测试样本训练集，将稳态电流特征输入到各种分类器中，对比在不同数据处理方式下的运算时间，实验结果见图5。由图5可知，在计算相同数量的负荷时，神经网络算法所用时间明显较长，并且随着负荷数量的增加，其增长速度呈指数倍。这是由于运用神经网络算法计算时，要求负荷的各种运行状态都要以样本的形式进行训练，训练过程需要多次的迭代，并进行大量的迭代计算，因此运算时间会大幅增加。通过细节放大图看出本文方法的运算时间明显低于传统CApEn值算法，并且随着负荷数量增加，其运算效率明显提高。

根据30次实验结果得到的数据，统计出运用不同方法识别各种家用负荷类型的准确率，结果见表2。由数据对比可知，本文算法对5类家用负荷的识别准确率均高于神经网络算法，且平均识别准确率高达97.33%，高于神经网络的80%，说明互近似熵方法在识别家用负荷方面准确性更高，更具有优越性。

图5 不同识别算法运算时间对比

表2 实验30次时不同方法识别准确率

5 结论

本文将家用负荷稳态运行时的电流波形作为特征量，提出了一种基于波形相似度匹配的家用负荷快速识别方法。与传统的互近似熵算法相比，该方法在运算过程中省去了大量的冗余计算，大大提升了运算速度，并且具有抗噪能力强、所需采样窗口短等优点。在家用负荷识别中，对特征量提取的质量要求不严格，也不需要大量的训练样本，有效避免了在负荷识别中不易全面提取负荷特征，以及采用神经网络分类器时，存在的所需训练样本大、不易收敛、计算过程复杂等问题。通过构建的小型多重负荷用电网络进行仿真实验，模拟了家用负荷识别的过程，验证了该方法可以有效地提高家用负荷识别的精度和效率，实现了对家用负荷的快速准确识别。