竖向偏心荷载作用下悬臂箱梁畸变效应研究

2021-03-13王妍张元海

铁道科学与工程学报 2021年2期

王妍，张元海

竖向偏心荷载作用下悬臂箱梁畸变效应研究

王妍，张元海

(兰州交通大学土木工程学院，甘肃兰州 730070)

在改进的箱梁畸变效应解析理论基础上，用能量变分法建立畸变控制微分方程，根据边界条件推导出两端设置横隔板的悬臂箱梁在竖向偏心均布荷载作用下的畸变效应计算式。通过有限元软件ANSYS对所推导公式的正确性进行验证。结合数值算例详细分析参数变化对悬臂箱梁畸变效应的影响。研究结果表明：高宽比对悬臂箱梁畸变翘曲正应力的影响程度大于对横向单宽弯矩的影响程度，当高宽比约为1.5时悬臂箱梁畸变效应最为显著；当高宽比和悬臂板相对宽度变化时，畸变翘曲正应力发生变号以及横向单宽弯矩出现峰值的截面位置也会改变；悬臂板相对宽度对畸变效应影响较小；荷载偏心率对畸变效应影响显著。

悬臂箱梁；能量变分法；畸变效应；翘曲正应力；横向弯矩

箱形截面由于具有结构性能良好、稳定性强、截面效率高等优点而在现代各种桥梁上都得到了广泛的应用。然而，随着其壁厚日趋减小，由截面畸变引起的翘曲正应力在箱梁桥总应力中所占的比例逐渐增大[1−2]。有关研究表明，简支箱梁截面由刚性扭转和畸变产生的纵向翘曲应力可达由活载和恒载共同作用的纵向弯曲应力的1/4左右[3−4]，而由截面畸变产生的横向弯曲应力大小可达到活载纵向弯曲应力大小的同一数量级[5−8]。畸变效应解析方法目前有等代梁法[1]、弹性地基梁比拟法[9−10]、广义坐标法[11]等。各种方法繁简程度以及对畸变变形未知量的选取和定义皆有不同，在分析过程中有些方法考虑剪切变形，有些方法则不考虑，许多学者研究得出剪切变形对畸变效应影响较小的结论[12−13]。国内外学者发表的相关论文几乎都以简支箱梁为例揭示畸变效应[14−20]，而针对悬臂箱梁畸变效应研究分析的文献较少[21]。然而桥梁施工方法中有些方法会使桥体在施工过程中处于悬臂状态，例如对称悬臂施工法、顶推法等。本文在改进的箱梁畸变效应解析理论基础上，推导了两端设置横隔板的悬臂箱梁在竖向偏心均布荷载作用下的畸变角、畸变矩、畸变双力矩的表达式，并结合具体算例详细分析了高宽比、悬臂板相对宽度、荷载偏心率等参数变化对悬臂箱梁畸变效应的影响。

1 畸变总势能

1.1 畸变基本未知量

单室梯形箱梁横截面畸变变形如图1所示，为形心坐标系，为过点且平行于正半轴的直线与腹板的交点，为轴与底板交点。为畸变中心，D为畸变角，其组成及截面变形如图2所示。定义箱梁周线坐标以逆时针为正，则上、下翼板和腹板沿的切向位移t可分别表达如下：

式中：0为截面形心到上翼板中面的距离；D为截面畸变中心的坐标；1为点到轴的距离；为梁高；为腹板俯角。

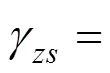
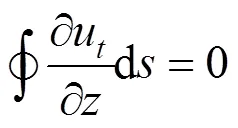
将式(1)代入式(2)可得：

式中：

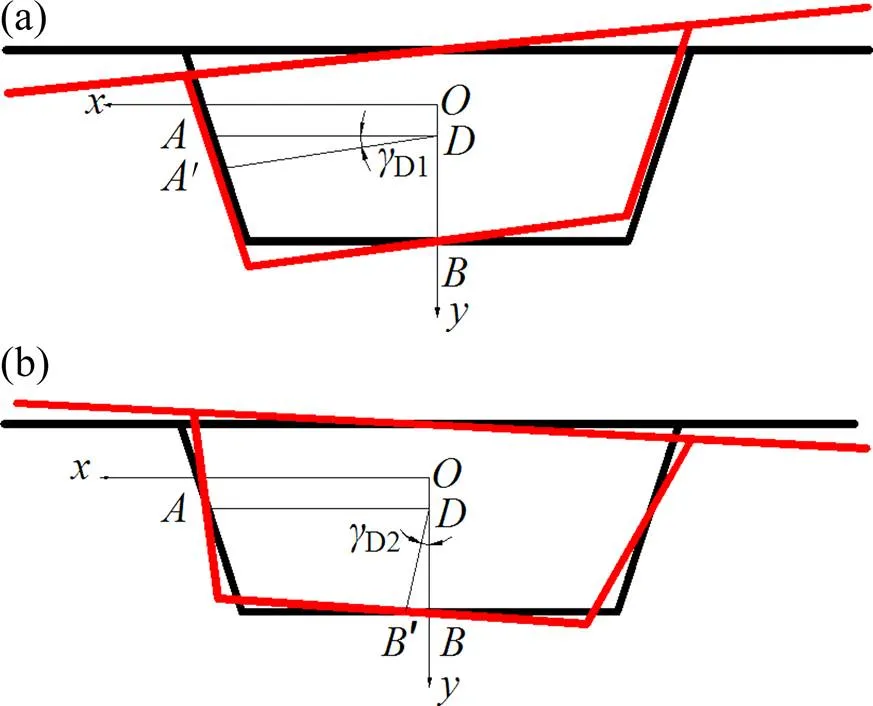
(a) γD1；(b) γD2

将式(3)代入式(1)，并根据zs=0，可得：

式中：

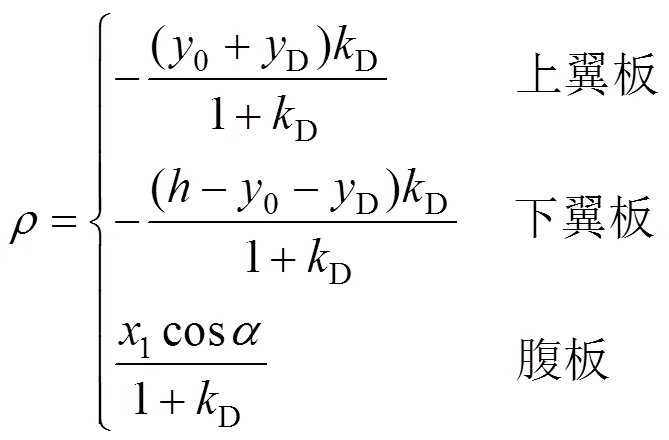
将式(4)对积分，可得：

D称为畸变扇性坐标，根据式(7)可计算出各个特征点的扇性坐标值，进而画出箱形截面扇性坐标分布图如图3所示。

图3中D1，D2和D3为上翼板左端点、腹板与上、下翼板交点处的扇性坐标，其表达式如下：

图3 畸变扇性坐标分布图

则根据弹性体物理方程可得：

记与D1，D2和D3相对应的特征点的翘曲正应力为D1，D2和D3，定义应力比为D2与D3的绝对值之比，则可得畸变中心的坐标为：

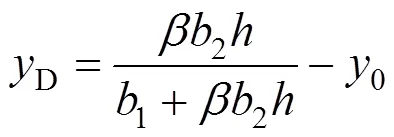
由于畸变荷载是自相平衡的，所以翘曲正应力对轴的力矩为0，可得应力比的表达式为：

式中：1，2和w为上、下翼板和腹板的厚度；1，2，3和w参见图1。

1.2 畸变翘曲应变能

根据式(8)可求得畸变翘曲应变能1为：

1.3 框架畸变应变能

由图2所示的畸变变形关系，可将箱梁截面上任一点沿着形心坐标轴，正向的位移分别表达为：

式中：w()为计算点所在水平线与腹板交点到轴的距离。

沿梁跨径方向截取单位长度梁段形成的横向框架进行分析，其变形如图4所示。将左腹板上下角点处的坐标(1，−0)，(2，0)代入式(12)可得2角点的横向位移分别为：

式中：

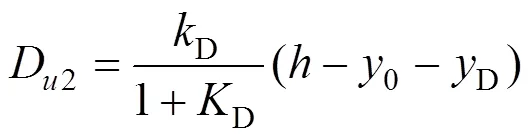
根据图4中各角点的位移方向，由两端固定等截面直杆的转角位移方程可得到角点1，2的杆端弯矩分别为：

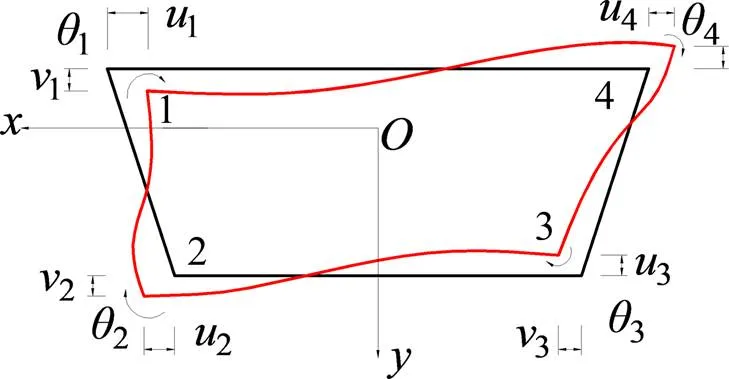
图4 横向框架畸变变形图

需特别注意3点：首先，转角位移方程中的各项都以顺时针为正；其次，图4中1的方向与规定的正方向相反，故式(14)和(15)中在其前面加了负号；最后，框架弯矩及其变位具有左右反对称性。

根据角点处杆端弯矩的平衡，将式(13)代入(14)和(15)式可得：

式中：

联立解出式(16)中的1和2后回代到式(14)和式(15)，就能得到图4中角点1，2的横向弯矩为(框架内侧受拉为正)：

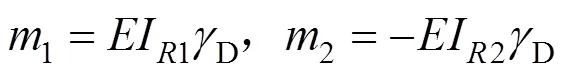
式中：

得到角点弯矩以后就可得出箱梁的框架畸变应变能2为：

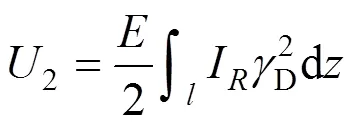
式中：

1.4 外荷载势能

若将箱梁上作用的竖向偏心荷载分解成的竖向反对称荷载记为D，则外荷载势能可表达为：

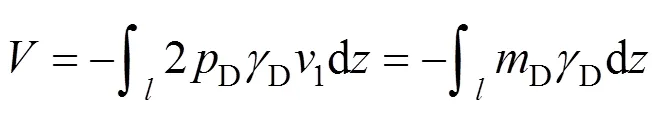
式中：D为分布畸变荷载。

1.5 总势能

畸变总势能为畸变翘曲应变能、框架畸变应变能和外荷载势能的总和：

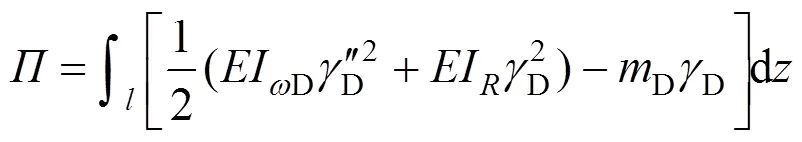
2 畸变控制微分方程

对式(20)进行一阶变分得：

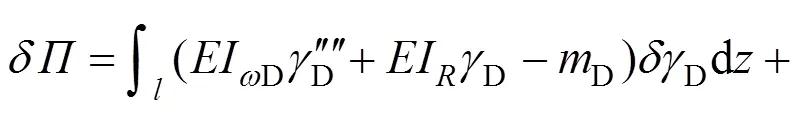
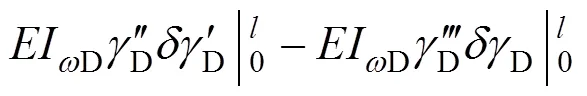
根据能量变分原理，令总势能的一阶变分为0，可得：

式(22)即为畸变控制微分方程，式(23)则为边界条件。

化简式(22)，可得：

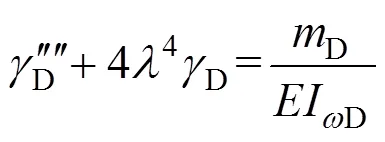
由边界条件式(23)可以得出畸变矩D及畸变双力矩D的表达式为：

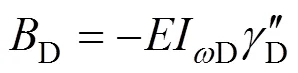
对于悬臂箱梁，当求解畸变微分方程式(24)时所用到的边界条件如下：

3 悬臂梁承受竖向偏心均布荷载

求解控制微分方程式(24)，可得箱梁在承受满跨均布畸变荷载D时的通解为：

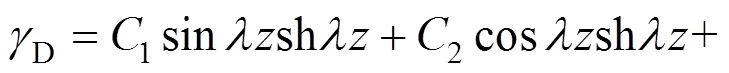
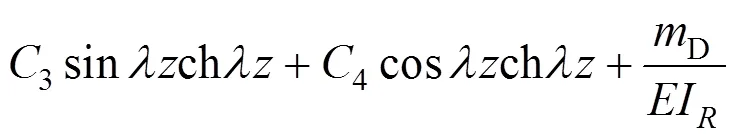
根据两端边界条件：

可求得式(26)中的4个积分常数分别为：

将1，2，3和4回代至式(26)即可得到悬臂梁承受均布畸变荷载D时的畸变角D的表达式，在此基础上，对D求两阶、三阶导数后代入式(25)即可得悬臂梁承受均布畸变荷载D时的畸变矩、畸变双力矩的表达式。为使表达式简洁，这里仍用1，2，3和4：

由式(8)和式(25)可得畸变翘曲正应力表达式：

至此，有关两端设置横隔板的悬臂梁承受均布荷载时的所有畸变相关量已得到求解，可直接利用本文推导的解析式(17)，(26)，(27)，(28)和(29)计算其横向单宽弯矩、畸变角、畸变矩、畸变双力矩和翘曲正应力。

需特别注意：文中式(1)～(25)普遍适用于梯形截面箱梁畸变效应的求解，而式(26)～(29)则只适用于两端设置横隔板的悬臂箱梁承受竖向偏心均布荷载时的畸变效应计算。

4 数值算例及参数分析

等截面悬臂箱梁跨度=40 m，其横截面尺寸如图5所示。图5中表示荷载偏心距，箱梁承受竖向偏心均布荷载=20 kN/m，材料弹性模量=35 GPa。箱梁只在两端设有横隔板。

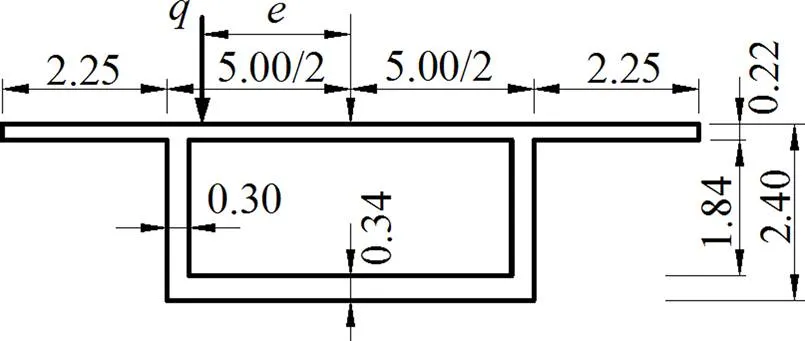
单位：m

定义高宽比为梁高与箱室宽度之比，悬臂板相对宽度为悬臂板宽度与箱室宽度之比，荷载偏心率为荷载偏心距与顶板半宽之比。

为了验证本文所得公式的正确性，在荷载偏心率=1时，将有限元软件ANSYS和按本文方法计算的跨中截面上翼板各计算点畸变翘曲正应力结果列于表1。计算点位置如图6所示。

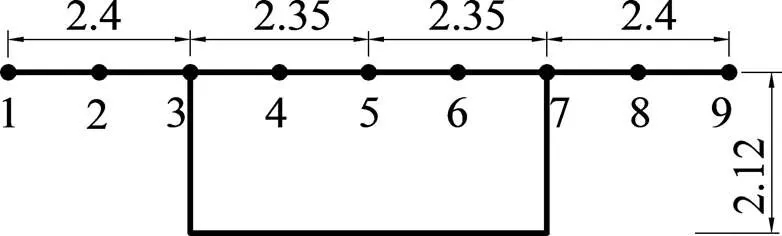
单位：m

ANSYS模型采用壳单元SHELL63，固定端节点采用全约束。施加荷载时，将作用在箱梁上的竖向偏心荷载分解成得到的箱梁各板元的畸变荷载等效均匀地施加在壳单元各节点上，如此，ANSYS模型得到的结果就为畸变效应结果。由表1可以看出，按本文所推公式计算的结果与ANSYS软件的计算结果总体上吻合良好。

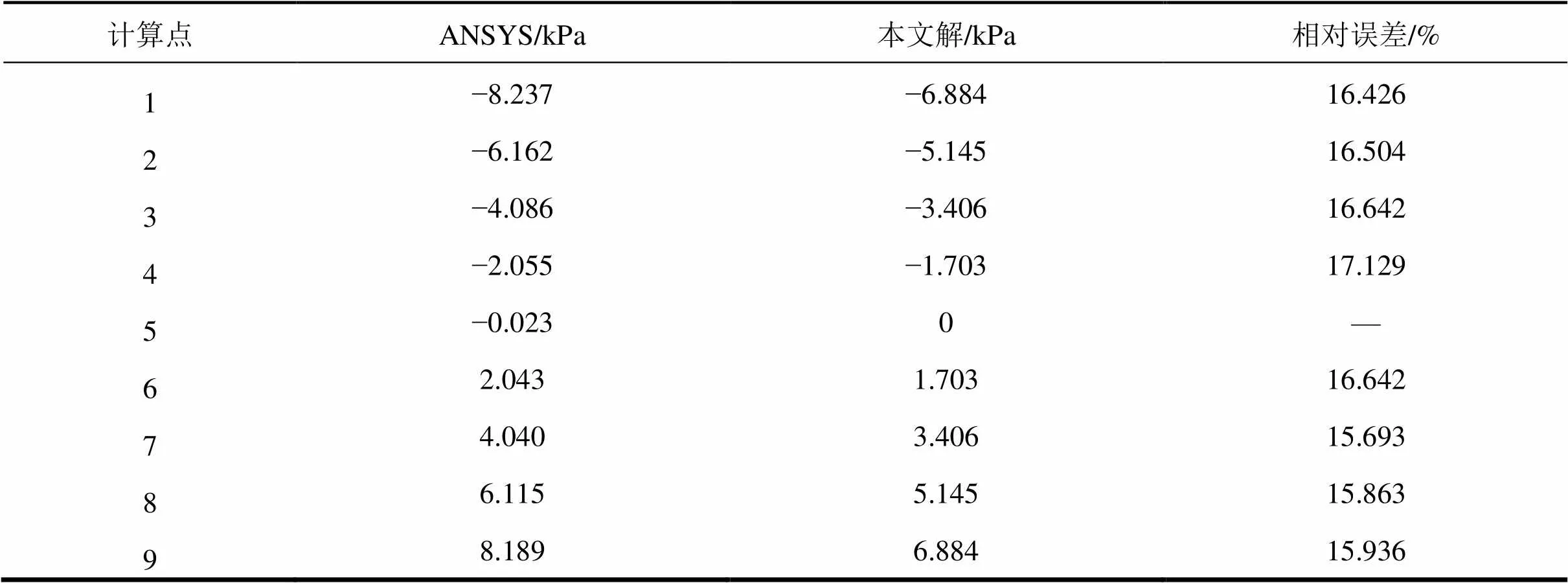
表1 跨中截面畸变翘曲正应力比较

注：相对误差=(ANSYS解−本文解)/ANSYS解×100%。

按本文方法计算得出的畸变翘曲正应力与横向单宽弯矩的纵向分布如图7所示。图7中D2，1为顶板与腹板交点处的畸变翘曲正应力与单宽弯矩值；D3，2为底板与腹板交点处的畸变翘曲正应力与单宽弯矩值。

由图7(a)可以看出：畸变翘曲正应力在跨内出现了变号，峰值出现在自由端，且D3大于D2(绝对值)；由图7(b)可以看出：横向单宽弯矩在纵向呈现先增大后减小的规律，且2大于1。

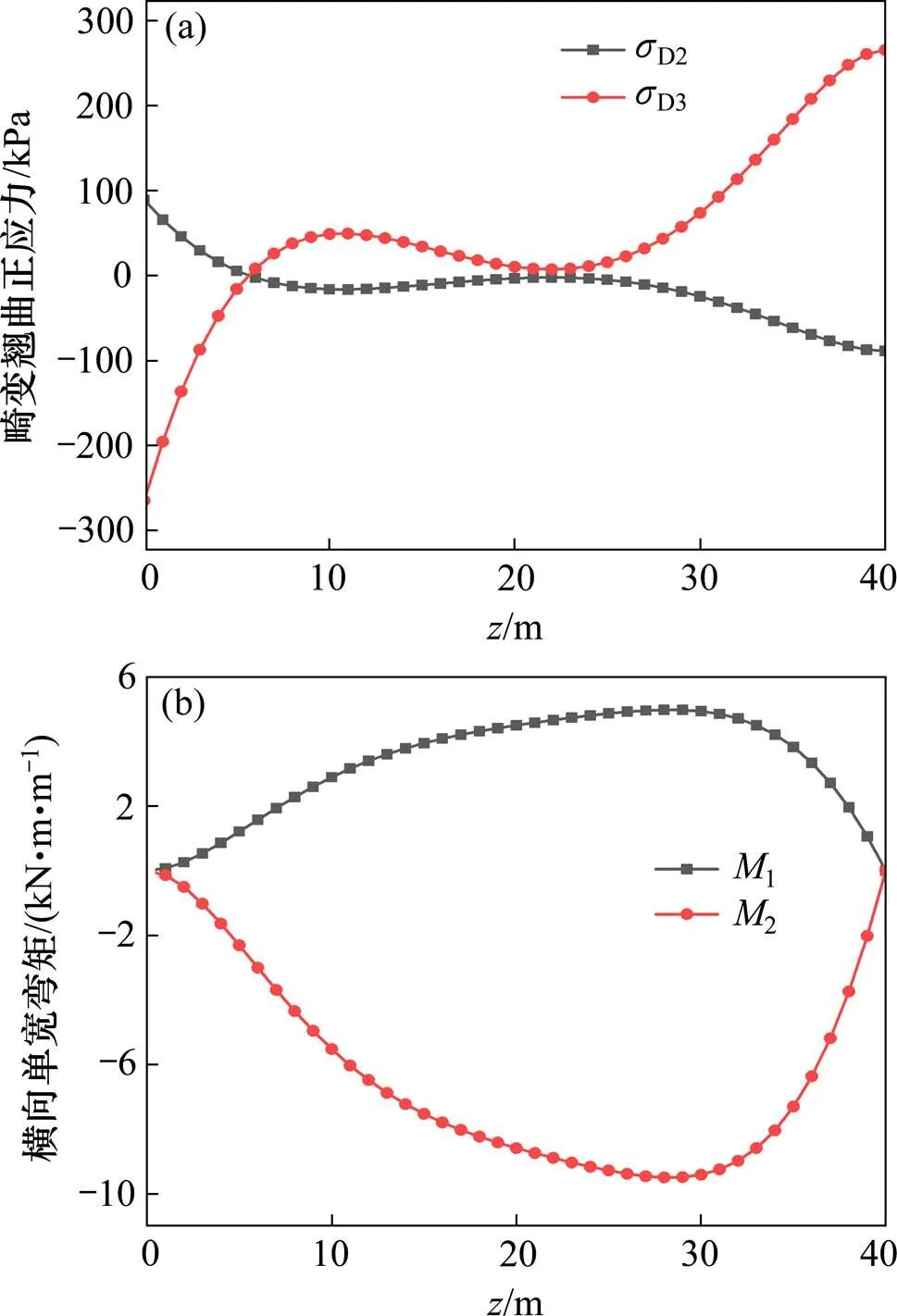
(a) 翘曲正应力纵向分布图；(b) 横向单宽弯矩纵向分布图

值得说明的是：图7(a)中畸变翘曲正应力出现了变号是因为悬臂箱梁两端设置了横隔板，因此在竖向偏心均布荷载作用下两端畸变角为0而跨内畸变角皆为正，进而导致畸变双力矩在跨内发生了变号；畸变扇性坐标D只与截面特性有关，不随而变(详见图3)，而畸变翘曲惯性矩ID总为正；则由式(29)可以看出，若畸变双力矩变号则畸变翘曲正应力也随之发生变号。

4.1 高宽比对畸变效应的影响

为了研究对畸变效应的影响，保持=40 m，3=2.4 m，=2.35 m不变，通过改变梁高可按本文公式求得变化时D3和2的纵向分布曲线以及D3峰值变化曲线如图8所示。

由图8(a)可以看出：随着的增大，D3的纵向分布曲线变化显著，从分段单调变为始终单调且发生变号的截面位置也逐渐右移，但峰值始终出现在自由端；由图8(b)可以看出：2的纵向分布曲线并无明显变化但随的增大其出现峰值的截面位置逐渐左移且绝对值也逐渐减小；对比图8(a)和8(b)可看出：对翘曲正应力的影响程度大于横向单宽弯矩；由图8(c)可以看出：随着的增大，D3的峰值变化剧烈，在约为1.5时达到峰值，也即此时悬臂梁畸变效应最为显著。

(a) ψ变化时σD3纵向分布；(b) ψ变化时M2纵向分布；(c) ψ变化时σD3峰值变化

4.2 悬臂板相对宽度对畸变效应的影响

为了研究对畸变效应的影响，保持=40 m，=2.12 m，=2.35 m不变，通过改变悬臂板宽度可按本文公式求得变化时D3和2的纵向分布曲线如图9所示。

(a)χ变化时σD3纵向分布；(b) χ变化时M2纵向分布

由图9(a)可以看出：随着增大，D3发生变号的截面位置逐渐右移；由图9(b)可以看出：随着增大，2出现峰值的位置逐渐左移；对比图9(a)和9(b)可看出：随着的增大，虽然D3与2的绝对值都逐渐增大，但增大的幅度很小，这说明悬臂板相对宽度变化对畸变效应影响较小。笔者针对箱室高宽比不同情况，又做了计算后发现，对扁宽悬臂箱梁，普遍存在悬臂板相对宽度对畸变效应影响较小的结论。

4.3 荷载偏心率对畸变效应的影响

为了研究对畸变效应的影响，保持=40 m，=2.12 m，3=2.4 m不变，通过改变荷载偏心距，可按本文公式求得变化时D3和2的纵向分布曲线如图10所示。

(a) ζ变化时σD3纵向分布；(b) ζ变化时M2纵向分布

由图10可以看出：荷载偏心率对畸变效应影响显著，越大，畸变翘曲正应力与横向单宽弯矩变化越剧烈；随着增大，D3与2呈线性增大，但D3发生变号和2出现峰值的截面位置不发生变化。

5 结论

1) 在改进的畸变效应解析理论基础上，用能量变分法建立了畸变控制微分方程，并根据边界条件推导出了两端设置横隔板的悬臂箱梁在竖向偏心均布荷载作用下的畸变角、畸变矩、畸变双力矩的解析表达式，以便工程应用。通过ANSYS有限元验证了本文公式的正确性。

2) 箱室高宽比对悬臂箱梁翘曲正应力的影响程度大于对横向单宽弯矩的影响程度。随着高宽比的增大，腹板与底板交点处翘曲正应力的最大值变化剧烈，当高宽比约为1.5时达到峰值，亦即此时悬臂箱梁畸变效应最为显著。

3) 随着箱室高宽比和悬臂板相对宽度的增大，腹板与底板交点处翘曲正应力发生变号的截面位置逐渐右移，而腹板与底板交点处横向单宽弯矩出现峰值的截面位置逐渐左移，但总是分别在距离固定端/8和3/4左右摆动，摆动幅度不超过跨径的15%；相较于悬臂板相对宽度，高宽比与荷载偏心率变化对悬臂箱梁畸变效应的影响程度更为显著。

4) 随着荷载偏心率的增大，腹板与底板交点处的翘曲正应力与横向单宽弯矩都呈线性增大，但翘曲正应力发生变号和横向单宽弯矩出现峰值的截面位置不会发生变化；荷载偏心率越大，畸变效应越显著。

[1] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008. GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design theory of box girder[M]. 2nd ed. Beijing: China Communications Press, 2008.

[2] 项海帆. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社, 2013. XIANG Haifan. Advanced theory of bridge structures [M]. 2nd ed. Beijing: China Communications Press, 2013.

[3] 李宏江. 波形钢腹板预应力混凝土组合箱梁扭转与畸变研究进展[J]. 建筑结构学报, 2017, 38(7): 59−67. LI Hongjiang. Review on torsion and distortion in prestressed concrete box girders with corrugated steel webs[J]. Journal of Building Structures, 2017, 38(7): 59− 67.

[4] 马磊, 万水, 蒋正文. 单箱双室波形钢腹板箱梁扭转与畸变性能研究[J]. 中国公路学报, 2016, 29(10): 77−85. MA Lei, WAN Shui, JIANG Zhengwen. Research on torsion and distortion performance of single box double-cell girder with corrugated steel webs[J]. China Journal of Highway and Transport, 2016, 29(10): 77−85.

[5] Kurian B, Menon D. Correction of errors in simplified transverse bending analysis of concrete box-girder bridges[J]. Journal of Bridge Engineering, 2005, 10(6): 650−657.

[6] Kurian B, Menon D. Transverse bending analysis of concrete box-girder bridges with flange overhangs[J]. Journal of Structural Engineering, 2008, 35(3): 173−179.

[7] 汪洋生, 张元海. 斜腹板薄壁箱梁横向内力分析及其参数影响研究[J]. 铁道学报, 2017, 39(3): 104−111. WANG Yangsheng, ZHANG Yuanhai. Research on transverse internal force and its parameter influence of thin-walled box girders with inclined webs[J]. Journal of the China Railway Society, 2017, 39(3): 104−111.

[8] 王兆南, 张元海. 单箱双室波形钢腹板组合箱梁横向内力研究[J]. 铁道学报, 2019, 41(12): 106−112. WANG Zhaonan, ZHANG Yuanhai. Research on transverse internal force of single box double cell composite box girder with corrugated steel webs[J]. Journal of the China Railway Society, 2019, 41(12): 106− 112.

[9] Wright R N, Abdel-Samad S R, Robinson A R. BEF analogy for analysis of box girders[J]. Journal of the Structural Division, 1968, 94(7): 1719−1743.

[10] Yao T Hsu, Chung C Fu. Application of EBEF method for the distortional analysis of steel box girder bridge superstructures during construction[J]. Advances in Structural Engineering, 2002, 5(4): 211−221.

[11] 韦芳芳, 吴京, 冯健, 等. 薄壁箱梁广义坐标法刚度矩阵的推导及应用[J]. 计算力学学报, 2007, 24(5): 693− 697. WEI Fangfang, WU Jing, FENG Jian, et al. Derivation and application of generalized coordinate method stiffness matrix of thin-wall box beam[J]. Chinese Journal of Computational Mechanics, 2007, 24(5): 693−697.

[12] 徐勋, 叶华文, 强士中. 考虑剪切变形的薄壁箱梁畸变分析[J]. 计算力学学报, 2013, 30(6): 860−866. XU Xun, YE Huawen, QIANG Shizhong. Distortion analysis of thin-walled box girder taking account of shear deformation[J]. Chinese Journal of Computational Mechanics, 2013, 30(6): 860−866.

[13] 王晨光, 张元海. 剪切变形对箱形梁畸变效应的影响[J]. 铁道学报, 2018, 40(5): 143−149. WANG Chenguang, ZHANG Yuanhai. Influence of shear deformation on distortion effect of box girders[J]. Journal of the China Railway Society, 2018, 40(5): 143−149.

[14] REN Yangzhi, WANG Bin, LI Yinqi, et al. New research for the distortion of steel box girders with inner solid diaphragms[J]. Advances in Structural Engineering, 2019, 22(14): 3026−3041.

[15] 王晨光, 张元海. 几何特性对薄壁箱梁畸变效应的影响[J]. 东南大学学报(自然科学版), 2020, 50(1): 89−95. WANG Chenguang, ZHANG Yuanhai. Influence of geometric characteristics on distortion effect of thin-walled box girders[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(1): 89−95.

[16] 邵江艳, 张元海, 赵庆友, 等. 波形钢腹板箱梁畸变应力分析[J]. 应用数学和力学, 2019, 40(10): 1109−1121. SHAO Jiangyan, ZHANG Yuanhai, ZHAO Qingyou, et al. Stress analysis on distortion of corrugated steel web box girders[J]. Applied Mathematics and Mechanics, 2019, 40(10): 1109−1121.

[17] 张元海, 王晨光, 林丽霞. 箱形梁布置双层悬臂板时的畸变效应分析[J]. 中国公路学报, 2016, 29(6): 214− 220. ZHANG Yuanhai, WANG Chenguang, LIN Lixia. Distortion effect analysis of box girders with double-level cantilever slab[J]. China Journal of Highway and Transport, 2016, 29(6): 214−220.

[18] 蔺鹏臻, 孙理想, 冀伟, 等. 时速250 km/h铁路双线箱梁的畸变效应研究[J]. 铁道科学与工程学报, 2016, 13(4): 595−599. LIN Pengzhen, SUN Lixiang, JI Wei, et al. Distortion effect of double track railway box girders with speed of 250 km/h[J]. Journal of Railway Science and Engineering, 2016, 13(4): 595−599.

[19] Jang G W, Kim M J, Kim Y Y. Analysis of thin-walled straight beams with generally shaped closed sections using numerically determined sectional deformation functions[J]. Journal of Structural Engineering, 2012, 138(12): 1427−1435.

[20] 王兆南, 张元海. 基于板元分析法的梯形截面箱梁畸变效应研究[J]. 铁道学报, 2020, 42(2): 102−109. WANG Zhaonan, ZHANG Yuanhai. Research on distortion effect of box girder with trapezoidal cross section based on plate element analytic method[J]. Journal of the China Railway Society, 2020, 42(2): 102− 109.

[21] 邓文琴, 毛泽亮, 刘朵, 等. 单箱三室波形钢腹板悬臂梁扭转与畸变分析及试验研究[J]. 建筑结构学报, 2020, 41(2): 173−181. DENG Wenqin, MAO Zeliang, LIU Duo, et al. Analysis and experimental study on torsion and distortion of single box three-cell cantilever girder with corrugated steel webs[J]. Journal of Building Structures, 2020, 41(2): 173−181.

Research on distortion effect of cantilever box girder under eccentric vertical load

WANG Yan, ZHANG Yuanhai

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Based on the modified distortion theory of box girders, the governing differential equation was established by applying energy variation method. The calculation formulas of distortion effect of the box girder with diaphragms in both ends subjected to the vertical eccentric uniform load were derived according to the boundary condition. The correctness of the formulas derived in this paper was verified through finite element software ANSYS. The influences of parameters on distortion effect of the box girder were analyzed through numerical examples. It is shown that the influence degree of height to width ratio on distortional warping normal stresses of cantilever box girder is more remarkable than the transverse unitwidth bending moment. The distortion effect of the box girder is most significant when the height to width ratio is approximately 1.5. The cross-section where the sign of distortional warping normal stresses changes and the peak value of transverse unit- width bending moment emerges vary with the height to width ratio and the relative width of cantilever slab. The relative width of cantilever slab has little influence on distortion effect. The load eccentricity has a significant effect on distortion effect.

cantilever box girder; energy variation method; distortion effect; warping normal stress; transverse bending moment