利用网络表征学习辨识复杂网络节点影响力

杨旭华，熊 帅

(浙江工业大学 计算机科学与技术学院，杭州 310023)

1 引 言

真实世界中的许多系统都可以抽象为复杂网络，比如社交网络、交通网络、电力网络、通信网络、人物关系网络、流行病传播网络等.辨识网络中有影响力的传播节点，涉及到网络的结构和功能等属性，包括度分布，平均距离，连通性，信息传播，鲁棒性等[1-3]，在实际应用中，能够控制信息在网络中的传播[4]、做高效的新闻推广[5]、避免电网中故障的传播[6]、分析蛋白质之间的相互作用[7]等.

如何有效辨识网络中节点传播影响力的大小，研究者们已经有了不少研究成果，这些方法总体上可以分为两种类型：基于局部信息和基于全局信息的判断节点中心性的方法.基于局部信息的方法，例如：度中心性[8]把节点连接的边的数量作为衡量的指标；邻居核中心性[9]把节点的一级邻居、二级邻居和三级邻居节点个数之和当做判断影响力大小的指标；K-shell分解方法[10]，是一种基于节点局部拓扑结构的方法，Liu等人[11]认为许多真实网络由于局部的紧密连接而存在类核结构，导致许多节点的值不能真实的反映节点在网络中的影响力，他们通过删除冗余边的策略，提高了K-shell值的准确性；郑文萍等人[12]衡量节点在网络连通性中的作用，通过节点所连边对局部网络连通性的影响来反映该节点在网络连通性方面的重要性；Chen等人[13]结合度中心性和全局信息，提出了一种半局部中心性方法，实验表现与紧密中心性相同，但计算复杂度较低；李维娜等人[14]，基于网络的局部社团结构和节点度的分布情况，提出了一种重要节点挖掘算法SG-CPMining.

基于网络全局信息的方法往往能获得比基于局部信息的算法更高的精确度，但计算复杂度比较高.例如介数中心性[15]和接近中心性[16]，都是基于全局路径的方法，考虑网络中任意节点对之间的路径.谷歌公司提出的PageRank[17]，通过考虑邻居节点的数量和质量，再进行全局的迭代计算来确定节点的重要性.吕琳瑗等人提出一种类似于PageRank的算法，在网络中增加了一个背景节点与所有节点进行双向连接，使新的网络成为强连通网络，称作LeaderRank[18].王斌等人[19]考虑网络的结构及属性信息，提出节点信任度的概念，同时将节点信任度引入到PageRank 算法中，构建了一种关键节点识别算法TPR(Trust-PageRank)；Lu等人[20]提出了一种基于信息扩散特性，将节点的局部属性与全局属性相结合的WeiboRank(WR)算法，在微博社交网络数据上表现良好.

上述辨识方法，都是建立在传统的网络表示方法之上的，普遍依赖于网络的邻接矩阵和拓扑结构，具有维度高和数据稀疏的特点，计算复杂度高，在大型网络使用中计算代价比较高.随着网络表征学习技术在自然语言处理等领域的发展和广泛应用，研究者们转而探索如何将网络中的节点表示为低维且稠密的向量，提出了诸多方法.DeepWalk是网络表征学习的先驱[21]，将词表示学习算法word2vec[22]应用在随机游走序列上，从而生成了节点的低维度表示向量.Line[23]针对一阶相似度和二阶相似度，提出了一种边采样算法优化目标函数，进而得到节点的向量表示.Node2vec[24]通过改变随机游走序列生成的方式扩展了DeepWalk算法，将宽度优先搜索和深度优先搜索引入了随机游走序列的生成过程，综合考虑了网络的局部信息和全局信息来表示节点.CANE[25]假设每个节点的表示向量由文本表示向量及结构表示向量构成，其中，文本表示向量的生成过程与边上的邻居相关，再利用卷积神经网络和注意力机制对一条边上两个节点的文本信息进行编码，得到节点的表示向量.SDNE[26]使用深层神经网络对节点表示间的非线性进行建模，把模型分为两个部分：一个是由 Laplace 矩阵监督的建模第1级相似度的模块，另一个是由无监督的深层自编码器对第2级相似度关系进行建模，将深层自编码器的中间层输出作为节点的向量表示.这些算法从不同的角度，采用不同的优化方法，把高维和稀疏的网络映射到低维和稠密的向量空间，保留网络的原有结构，具有计算复杂度低和准确度高等特点.

在本文中，我们基于网络表征学习提出了一种辨识网络节点影响力的方法.采用网络表征学习DeepWalk算法把高维的复杂网络映射到低维的向量空间，把网络节点映射为欧式空间中低维的向量表示，然后结合网络拓扑信息提出节点的局部中心性，作为判断节点影响力大小的指标.

2 基于网络表征学习的节点局部中心性

节点在网络中传播信息时，与其局部的拓扑结构有很大的关系.已有研究表明：节点的K-shell值越大，周围的拓扑结构越紧密，节点向周围区域传播信息的效率越高[27]，同时，信息传递的强度随着节点间距离的增大而迅速衰减[28]，由此，提出一种基于网络表征学习和局部中心性确定任意节点i的影响力指标：

(1)

其中，Ksi表示节点i的K-shell值，χi、χj分别表示节点i、j用DeepWalk网络表征方法映射到低维欧式空间的向量， |χi-χj|表示两个向量之间的欧氏距离，Γ(i)表示i节点的三级邻域，即i节点的一级邻居、二级邻居以及三级邻居节点的集合，j节点属于Γ(i)集合.

网络中节点间的距离，本文没有采用网络的最短路径距离，因为会存在如下的问题，如图1所示，i节点在传播它自身的信息时，首先会影响它的一级邻居节点，比如节点k和节点j，当节点k和j被感染后，由于j节点有更多的连接到外部区域的邻居节点(图1中灰色节点)，尽管同样是节点i的一级邻居节点，j比k在传播i节点信息的过程中贡献更大[29]，所以，信息在网络中的传播，除了距离以外，还与网络的结构密切相关，最短路径距离的长度不能准确的表示信息在传播过程中的衰减，还要根据网络的拓扑结构，对所求节点的邻域节点做进一步的划分.

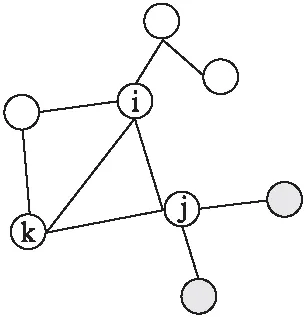
图1 一个有8个节点和9条边的网络Fig.1 Network with eight nodes and nine edges

因为网络表征学习方法不但可以把高维网络映射到低维的向量表示，而且可以同时保持网络的结构，节点间的距离用低维向量间的欧式距离替代后，不仅考虑了最短路径距离，而且包含了节点周围的拓扑结构信息，能够更准确的描述信息在网络传播过程中的衰减.因此在本文中，我们选择应用DeepWalk方法，把网络节点映射到低维的向量表示，然后用节点相应的低维向量来计算节点之间的距离.

具体地，基于DeepWalk方法，将网络空间映射到欧式空间，把每一个节点表示为一个低维稠密的向量，将具有N个节点的网络G转化为欧氏空间的N个r维向量，一个网络节点及其连边信息对应一个向量，其中任意节点i的向量表示为：

在本文中，r取N/2

3 实验和分析

3.1 数据集

为了评估所提出的方法的性能，我们在8个真实世界的网络中进行了实验，这8个网络都是无向网络，也不考虑权重，它们分别是常见形容词和名词的邻接网络adjnoun[30]、科学家合作网络netscience、Ca-GrQc和hep-th[31-33]、新西兰宽吻海豚社会网络dolphin[34]、小型的facebook社交网络[35]、爵士音乐人合作网络Jazz[36]、美国政治图书网络polbooks[37]，表1给出了8个真实数据集的拓扑属性参数.其中，N和E分别表示网络的节点数和边数，〈k〉表示网络的平均度，在本文中，考虑到现实世界中网络的度分布往往存在“重尾效应”，令βth=〈k〉/〈k2〉[38]，表示SIR模型传播的阈值，c表示网络的平均聚类系数.

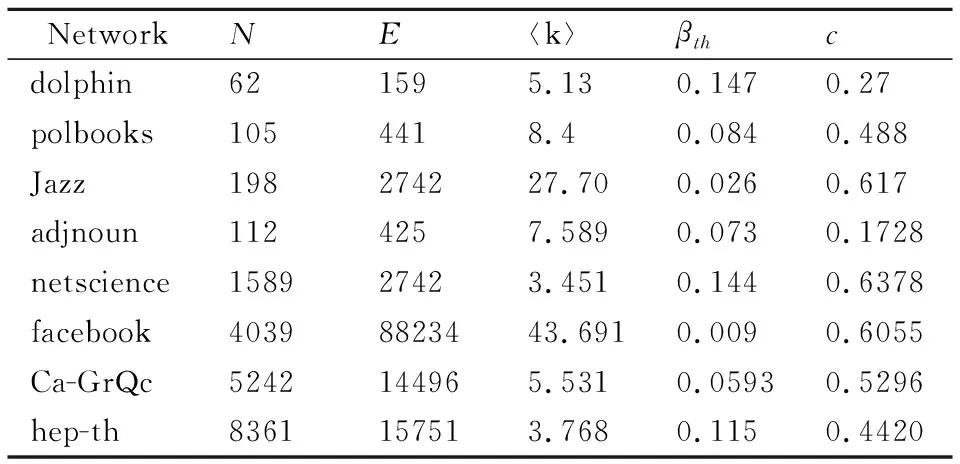
表1 数据集Table 1 Data sets

3.2 评价方法和指标

3.2.1 SIR疾病传播模型

SIR属于动态传播算法，结果准确性好但计算复杂度高，本文提出的NLC算法及其他静态指标方法计算复杂度低，我们用SIR疾病模型做为基准参照模型去评价不同的判断节点影响力静态指标方法性能的优劣[39].在SIR模型中，如果需要判定一个节点在网络中的传播影响力，则把这个节点设定为网络中唯一的感染节点(Infected)，其他节点标记为易感节点(Susceptible)，在每个时间步，每个感染态节点会以概率β(β=1.5βth)感染其易感邻居节点，βth表示SIR模型传播的阈值，然后以概率μ(在本文中，我们设置μ=1)从疾病中恢复，变成移除态(Recovered)，移除态节点不会再被感染.这个过程不断迭代直到网络中没有感染节点为止，t时刻网络中移除态和感染态节点的总数量，记为F(t)，F(t)，作为评价t时刻该节点传播影响力大小的指标，F(t)越大，该节点影响力越大.

3.2.2 SI疾病传播模型

在该模型中，节点一旦被感染，状态从S变为I之后不能恢复，其他条件和SIR模型相同，在本文中，易感状态节点被感染的概率为2βth.如果在相同的时间步的条件下，一个节点感染的网络节点越多，则说明该节点感染能力越强，影响力越大.

3.2.3 肯德尔系数

不同的方法都可以按照所计算的传播能力，对网络中所有节点从高到低排序，针对不同的感染率β，我们用肯德尔系数τ去评价不同的静态指标方法得到的排序列表和SIR动态传播模型生成的排序列表之间的联系[40]，τ是一个在[-1，1]之间的一个数，τ越大，两个序列吻合度越高，τ被定义为：

(2)

Nc表示两个排序列表相协调元素的数量，Nd表示二者不协调元素的数量，N表示网络节点总数.

3.3 数值仿真

首先，对八个真实网络的每一个节点在本网络内赋予唯一的编号，比如网络1有N个节点，则网络节点的编号应该是1，2，……，N.

3.3.1 比较NLC和5种知名中心性方法识别的Top-10高影响力节点的准确性

在表2中，我们以SIR模型计算出来的Top-10节点为基准，在4个真实网络上，用NLC方法，度中心性(DC)、接近中心性(CC)、介数中心性(BC)、邻居核中心性(Cnc)、半局部中心性(CL)分别计算Top10节点，比较不同方法的准确性，考虑到网络的规模和时间复杂度，本文令t=10[41].具体计算方法为：以dolphin网络为例，首先用SIR模型在t=10时刻，计算得到F(10)数值最大的Top-10节点做为基准，然后用NLC方法算出Top-10节点，如果两组节点有9个相同，则NLC算法的准确率为90%.

表2 6种中心性算法和SIR模型对排名前10节点的识别结果Table 2 Six algorithms and SIR models to identify thetop-10 nodes

在表2中，比较其它5种方法，本文提出的NLC算法在4个数据集中都取得了最高的准确率.接下来，我们比较了各种静态指标算法与SIR模型得到的Top-10节点排序列表的吻合程度，在小型网络polbooks和adjnoun中，6种中心性算法都有较高的准确率，CL算法和NLC算法有相同的准确率，但NLC得到的序列与SIR模型给出的序列更吻合；在dolphin和netscience网络中，NLC算法不仅有最高的准确率，而且给出的排序序列与SIR模型给出的序列更吻合；就整体而言，NLC与SIR模型得到的序列保持良好的吻合度.

其中实验结果取1000次实验的平均值，最佳准确率用黑体字标出，F(10)表示SIR模型在第10时间步的结果.

3.3.2 比较NLC与5种知名中心性方法在SIR模型下的肯德尔系数

分别用各种静态指标算法与SIR模型对一个网络中所有节点的影响力排序，然后比较各种静态指标算法得到的节点排序列表和SIR模型得到列表的吻合程度，我们用肯德尔系数表示这个吻合程度.

如图2所示，针对不同的感染率β，使用NLC和5种知名中心性方法计算出网络中所有节点的影响力大小排序列表，与SIR模型生成的排序列表做对比，得到肯德尔系数τ.在adjnoun网络中，BC算法表现最差，CL和Cnc算法表现基本相同，NLC算法表现最好；在polbooks网络中，CC和BC表现最差，NLC、CL、Cnc表现良好；在netscience网络中，表现最差的还是BC算法，CC和CL算法也表现不佳，当β<0.04，NLC算法表现最好，总体表现良好；在facebook网络中，CC表现最差，当β>0.04，NLC表现最好；在hep-th网络中，当β<0.04时，NLC算法表现最好，当β>0.04，NLC算法在6种方法中排名第二；dolphin网络中，当β在0到0.04以及0.07到0.1这两个区间时，NLC算法表现最好，优于其它算法；在Jazz和Ca-GrQc网络中，BC算法表现最差，当β>0.03时，NLC算法表现最好；综上所述，NLC在肯德尔系数上表现最佳.

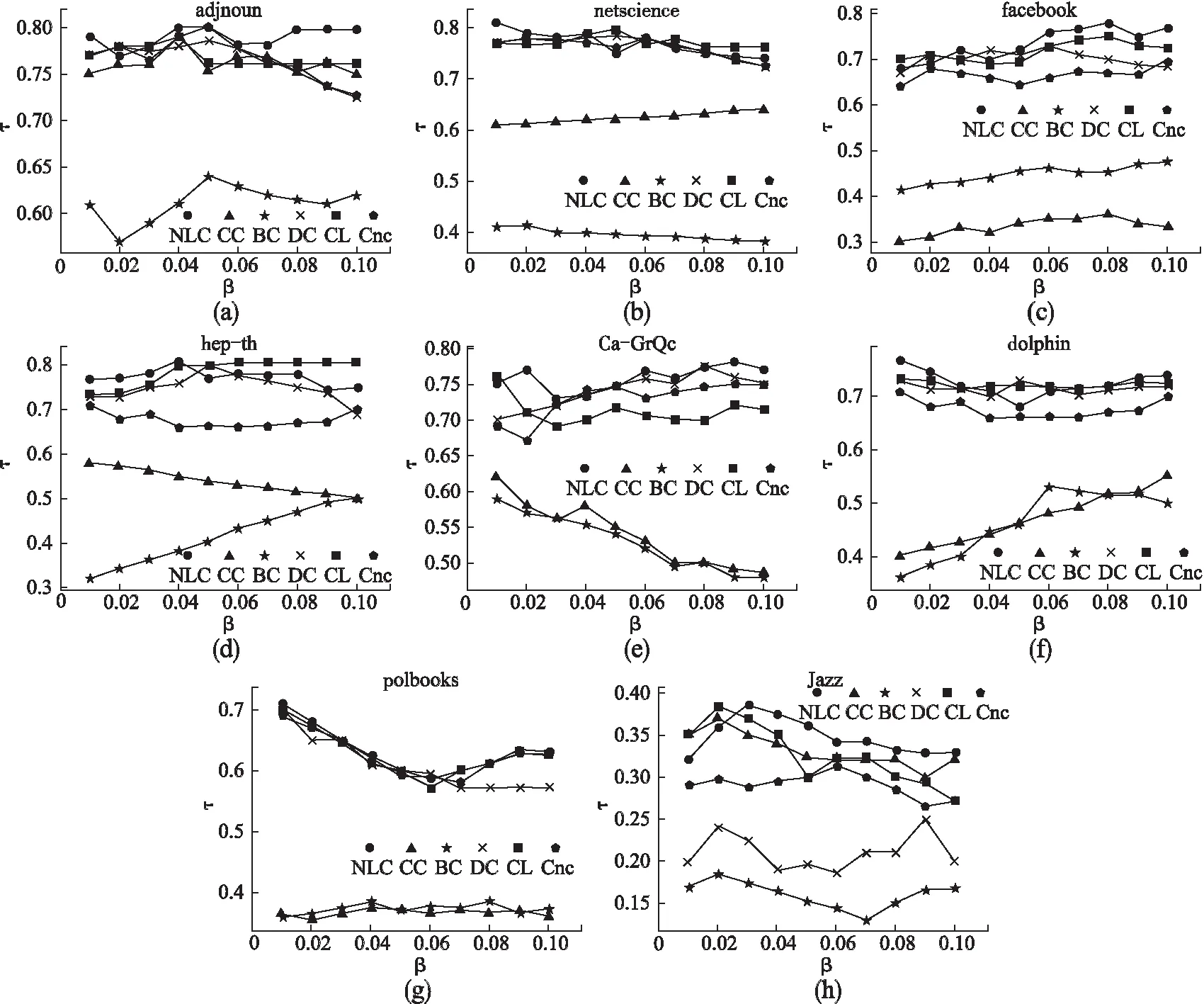
图2 NLC，CC，BC，DC，CL，Cnc算法的肯德尔系数，取1000实验的平均值.横坐标表示节点被感染的概率，纵坐标表示肯德尔系数Fig.2 Kendall correlation coefficient of NLC，CC，BC，DC，CL，Cnc algorithm which are taken as the average value of 1000 experiments.The horizontal ordinate represents the probability of the node being infected，and the longitudinal ordinate represents the Kendall correlation coefficient

3.3.3 比较NLC和CL、Cnc方法所选Top-10节点的平均感染能力

在8种不同的网络中，NLC算法性能均排前列;BC和CC算法不仅计算量大，而且表现差;Cnc算法和CL算法，在不同的数据集中，表现极不稳定，在有些数据集中表现较好，在有些数据集中甚至差于BC和CC算法.为进一步比较NLC，CL以及Cnc算法的性能，我们使用SI模型检验3种算法性能.

首先用一个算法选出Top-10节点，然后用Top-10节点在第t个时间步之内感染的节点总数与网络节点总数的比值的平均值

(3)

做为该算法的性能指标.在式(3)中，n表示网络节点总数，nit表示Top-10节点中第i个节点第1到第t步感染的节点总数.在相同的时间步和感染概率的情况下，哪一种方法选出的Top-10节点感染的节点越多，可以认为该算法表现越好.

具体实验结果如图3所示，可以看到，NLC算法在4个网络中都取得了最佳性能.在dolphin网络中，NLC算法表现最好，Cnc算法性能最差；在netscience网络中，当时间步大于15后，NLC算法感染的节点比另外两种算法明显增多，达到稳定的时间也比另外两种算法早，所选Top-10节点表现最好；在Ca-GrQc网络中，时间步小于10时，3种算法表现相近，大于10后，NLC算法表现最好，且NLC算法在第33个时间步就达到稳定；在hep-th网络中，Cnc算法表现最差，在第42个时间步才达到稳定，NLC算法表现最好.

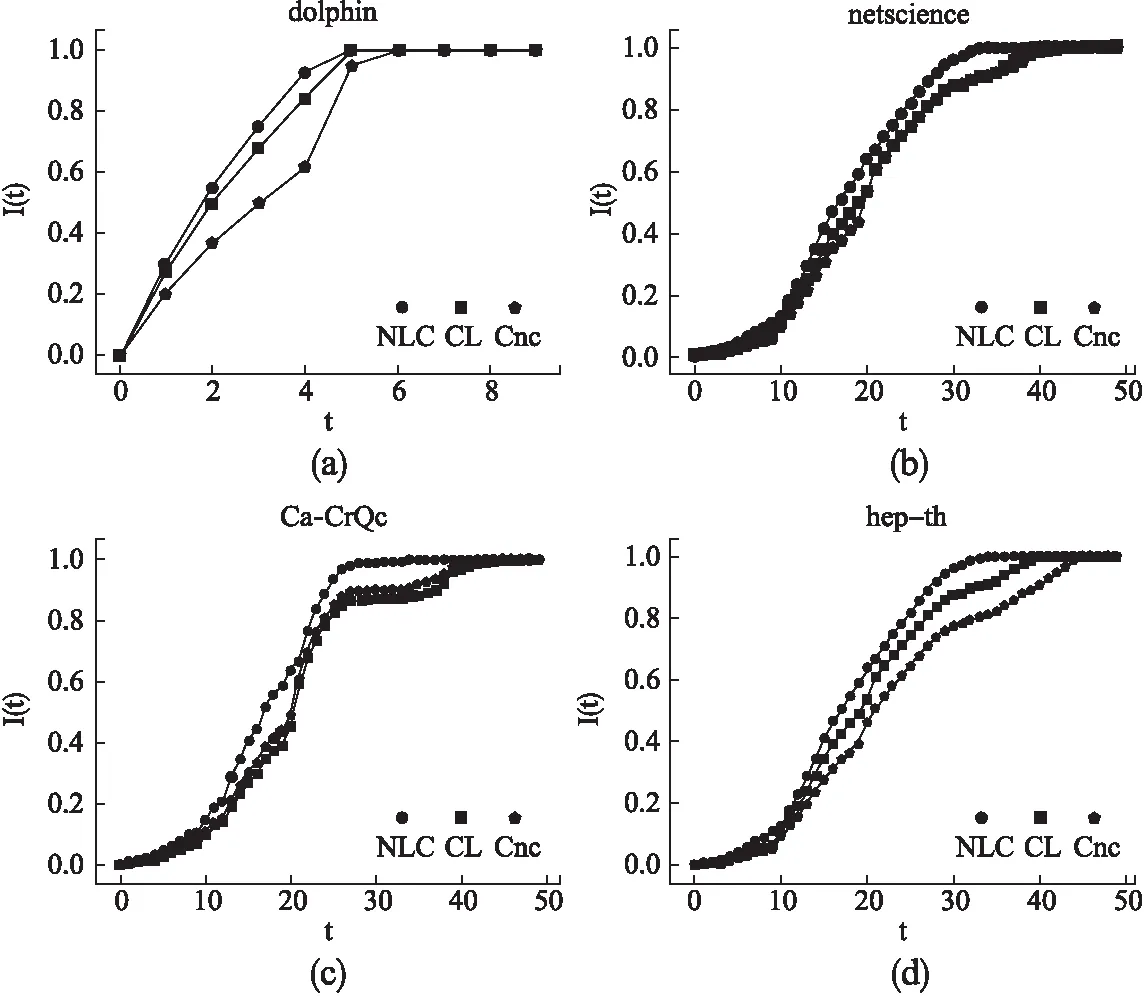
图3 Top-10节点的感染能力和时间步的关系曲线，取1000次实验的平均值.横坐标表示时间步，纵坐标表示第t个时间步内Top-10节点在SI模型中感染的节点数的平均值与网络节点总数的比值Fig.3 Relationship curve of infection ability and time step of Top-10 node.The results are taken the average of 1000 experiments. the horizontal ordinate represents the time step，and the longitudinal ordinate represents the ratio of the average number of nodes infected by Top-10 nodes in the SI model to the total number of network nodes within the t time step

4 总结和分析

在本文中，我们基于网络表征学习方法，结合节点的拓扑结构和邻域信息，提出了一种节点局部中心性指标来识别节点影响力的方法.该方法提出网络中的节点的影响力由拓扑结构决定，同时随着距离的增加而衰减.在8个真实网络中，通过和5种知名的中心性方法相比较，在计算Top-10节点、Top-10节点的感染能力和肯德尔系数等方面，NLC算法取得了良好的辨识效果，在分析和控制复杂网络中的信息传播过程中具有广阔的应用前景.