一种鲁棒性的少样本学习方法

代磊超，冯 林，杨玉亭，尚兴林，苏 菡

(四川师范大学 计算机科学学院，成都 610101)

1 引 言

近年来，深度学习在图像、语音、自然语言处理等多个研究领域取得了成功应用.但是，现有的少样本学习模型大多需要标注足够多的训练数据，这个过程需要花费大量的人力与物力.而少样本学习只需标记少量样本，就能建立具有较高识别率的模型.因此，少样本学习成为目前机器学习研究领域的热点.

现有的少样本学习方法可总结为四类：基于元学习(Meta-learning)的方法、基于数据增强的方法、基于迁移学习(Transfer Learning)的方法和基于度量学习(Metric Learning)的方法.

元学习：基于元学习的目标是训练元学习模型，模型可以在多种不同学习任务上达到很好的效果.例如记忆增强神经网络模型(Memory-Augmented Neural Networks)是基于神经图灵机(Neural Turing Machine,NTM)提出的，它能在外部存储器模块作用下实现内容的存储访问[1]；模型无关自适应(Model-Agnostic Meta-Learning,MAML)使用少量迭代步骤就可得到很好的泛化性能，并且模型微调简单，无需关心模型形式，也不需增加新的参数，直接用梯度下降进行训练[2]；Ravi等人提出基于长短期记忆网络(Long Short-Term Memory,LSTM)的元学习(Meta LSTM)，它学习的是一个模型参数的更新函数或更新规则，不是在多轮episodes学习一个单模型，而是每个episode学习特定的模型[3]；元网络(Meta Net)由两个学习组件组成，一个基础学习器在任务输入空间执行，一个元学习器在任务不可知元空间执行，并且配备了一个外部存储器[4]；基于梯度下降(Stochastic Gradient Descent,SGD)的元学习(Meta SGD)可以学习更新方向和学习速率，并且可以在每个episode中进行有效的学习[5]；转换传播网络(Transductive Propagation Network,TPN)在元学习框架下加入传导机制，即标签传播来应对数据少的问题[6].

数据增强：基于数据增强的少样本学习方法通过对数据集进行平移、旋转、变形、缩放等操作，生成更多样本以创建更大的数据集，防止过拟合[7]，例如元生成网络(Meta Generative Adversarial Networks,Meta-GAN)为特定任务生成增强数据，以补充训练数据[8].

迁移学习：基于迁移学习的方法智能地应用以前学到的知识来更快地解决新问题[9].通过继续训练来微调预训练网络的权重来达到迁移的目的[10]，例如Hariharan B等人提出了一个由用于特征提取和分类的学习者、表示学习阶段、少样本学习阶段以及测试阶段几部分组成的深度神经网络[11].

度量学习：基于度量学习的方法通过计算不同类别样本特征，使相同类别的样本彼此接近，不同样本彼此远离，例如原型网络(Prototype Network)认为每个类别都存在一个原型表达，该类的原型是支持集在嵌入空间的均值[12]；匹配网络(Matching Network)是基于记忆和注意力机制的网络[13]；关系型网络(Relation Network,R-Net)定义了一个由用于特征提取的嵌入模块和用于计算相似度的关系模块组成的模型[14]；元学习半监督少样本学习模型(Semi-supervised Few-Shot Learning,Meta SSL)利用半监督的方式对原型网络进行了改进[15].另外图神经网络(Graph Neural Network,GNN)定义了一个图神经网络框架，将每个样本看成图的节点，学习节点和边的嵌入，通过度量学习进行分类[16].

上述模型均是在特征清晰且无噪声的环境下训练，以达到较好的分类目的，而在实际应用中，因为图像采集设备、自然环境、光照、姿态等诸多因素的影响，模型所处理的图像并不会像数据集中的图像一样清晰[17]，因此在噪声的不确定环境中，模型泛化能力较弱.

为了解决这一问题，使少样本学习更具鲁棒性和可扩展性，本文提出了一种鲁棒性的少样本学习方法RFSL(Robust Few-Shot Learning,RFSL).

本文的主要贡献如下：

1)泛化性方面，采用关系网络的嵌入模块提取支持集与查询集样本特征，根据关系模块度量支持集与查询集样本的距离，端到端的训练多个基分类器，形成异构的基分类器模型.采用投票的方式对各基分类器最末的Sigmoid层非线性分类结果进行融合.利用此方法训练可使少样本分类模型具有更强的鲁棒性以及面对新域时更好的泛化性.

2)收敛性方面，模型采用KDE与滤波技术向训练任务的数据集加入多种类型随机噪声进行训练.此方法可模糊样本特征，促进少样本学习快速收敛，同时验证噪声参与训练的方式能有效帮助模型形成多个异构的基分类器.

3)根据模型准确率、计算效率、鲁棒性、离散度多个评价指标分析模型，从而提升研究效度.

本文的组织结构如下：第2节介绍相关理论基础；第3节详细介绍了本文方法；第4节是本文方法的实验，并给出实验结果与分析；最后对全文进行总结.

2 相关理论基础

2.1 问题定义

为了方便叙述，用数学的形式化方法定义少样本学习的相关基本概念.

定义1.(少样本数据集)设数据集D为一个三元组D=(X,Y,f)，其中：

X为输入空间，它由|X|个输入实例{x1,x2,…,x|X|}构成.本文中，∀xi∈X，xi表示输入的图片实例.

Y为输出空间，它由|Y|个类标签{y1,y2,…,y|Y|}构成.

f:X→Y为信息函数，它指定X中每一个输入实例的类别标签值，即∀xi∈X，∀yj∈Y，有f(xi)=yj成立.

∀yj∈Y，若f-1(yj)={xi∈X|f(xi)=yj}，称f-1(yj)为类标签yj的实例集.

特别地，如果|Y|=C，f-1(yj)=K，通常当K较小时，称D为C-way，K-shot少样本数据集.

其中，|·|为集合的势，i=1,2,…,|X|；j=1,2,…,|Y|.

在少样本学习中，需要在一个大的源域数据集Ds=(Xs,Ys,f)上按一定方法抽样生成多个C-way，K-shot少样本数据集，然后在这些小样本数据集上训练分类模型，并把分类模型较好迁移到目标域数据Dt=(Xt,Yt,f)上，Ds与Dt需满足Ys∩Yt=Ø.

定义2.(C-way，K-shot少样本训练任务、支持集与查询集)：给定数集Ds=(Xs,Ys,f)，Str=(XS,YS,f)，Qtr=(XQ,YQ,f)，从YS中随机抽取C个类{yj|j=1,2,…,C}，一个C-way，K-shot少样本训练任务定义在T=(Str,Qtr)上，满足：

①YS=YQ={yj|j=1,2,…,C}；

②∀ym∈YS，|f-1(ym)|=K；

③∀yn∈YQ，|f-1(yn)|=q；

④Str∩Qtr=∅.

其中，Str、Qtr分别称为训练任务支持集、查询集.

定义3.(C-way，K-shot少样本测试任务、支持集与查询集)：给定数据集Dt=(Xt,Yt,f)，Ste=(Xe,Ye,f)，Qte=(Xh,Yh,f)从Yt中随机抽取C个类{yj|j=1,2,…,C}，一个C-way，K-shot少样本测试任务定义在R=(Ste,Qte)上，满足：

①Ye=Yh={yj|j=1,2,…,C}；

②∀ym∈Ye，|f-1(ym)|=K；

③∀yn∈Yh，|f-1(yn)|=p；

④Ste∩Qte=∅.

其中，Ste、Qte分别称为测试任务支持集、查询集.

定义4.(C-way，K-shot少样本学习)：给定训练任务集合Tasks={(Str,Qtr)}、测试任务集合Tasks={(Ste,Qte)}，C-way，K-shot小样本学习任务是在多个训练任务的数据上，学习一个分类函数F*，并在测试任务的支持集Ste上，学习分类函数f*=F*(Ste)，使f*完成对测试任务中查询集的分类.其学习过程如下：

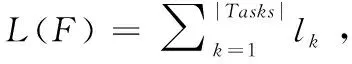
②测试阶段：对测试任务集的测试任务，利用支持集Ste，生成分类模型f*=F*(Ste)，然后使用查询集Qte完成对f*的评估.

特别地，在训练F*的过程中，如果涉及模型超参数的调整，也可以把训练任务集再划分为训练任务集与验证任务集.

对于定义4中少样本的定义，存在两种特殊的情况：

当K为1时称此任务为单样本学习，每次训练只给出一个类的单张图片作为支持集，剩下的图片作为查询集.

少样本学习另一种特殊情况为零样本学习，零样本学习并不是完全不需要训练样本，而是研究对于特定类训练样本缺失时，利用训练集样本和样本对应辅助文本描述、属性特征信息对模型进行训练.

2.2 深度卷积神经网络

卷积神经网络(Convolutional neural networks,CNNs)[18]是深度学习中代表算法之一.如图2为卷积神经网络关键流程，CNNs在处理图片这种二维结构数据取得巨大成功，它可将图片的多层二维数据通过卷积、正则化、池化、非线性激活函数映射以及全连接网络，提取出高层的语义特征.模型所涉及的卷积、池化以及激活函数如公式(1)-公式(4)所示.

卷积公式：定义Cov=Am×n⊗Bk×l为卷积操作，其中Am×n表示m×n的输入矩阵，⊗表示卷积运算符，Bk×l表示卷积核(大小为k×l)，Cov表示卷积后的矩阵.∀i∈[0,m)，∀j∈[0,n)，得：

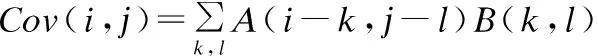
(1)

最大池化公式：定义P=MAP(Am×n,Bk×l)为最大池化操作，其中MAP(·,·)表示最大池化运算符，Am×n表示m×n的输入矩阵，Bk×l表示池化核(大小为k×l)，P表示池化后的矩阵.∀i∈[0,m)，∀j∈[0,n)，可得：

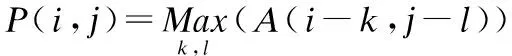
(2)

Sigmoid函数公式：定义S=Sigmoid(i)为Sigmoid激活操作，其中Sigmoid(·)表示Sigmoid运算符，S表示激活后的数值.∀i，有：

(3)

ReLU函数公式：定义R=ReLU(i)为ReLU激活操作，其中ReLU(·)表示ReLU运算符，R表示激活后的数值.∀i，有：

R(i)=max(0,i)

(4)

2.3 核密度估计与图像滤波方法

核密度估计的随机噪声添加方式：首先，读入图片得到其像素矩阵.其次，选用不同类型核函数K(·)，利用平均积分平方误差(Mean Interguated Squared Error,MISE)确定核函数带宽h.然后，利用该核函数对像素值做核密度估计(Kernel Density Estimation,KDE)，计算和筛选相应像素值.最后，转化添加噪声后的矩阵为对应图片并输出.平均积分平方误差如公式(5)，核密度估计如公式(6).

平均积分平方误差公式：定义h=MISE(x)，其中x为样本点，MISE(·)为平均积分平方误差操作，h为选定的带宽值，对于核函数K(·)，对任一给定样本点的概率密度f(x)与拟合后的核计算概率密度值f(x)，有：

(5)

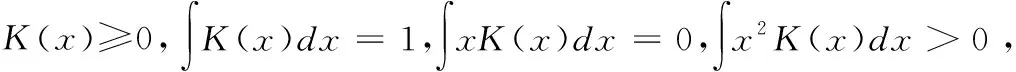
(6)

图像滤波噪声添加方式：利用不同核的滤波器，采用图像滤波(Image Filtering)技术对图像像素矩阵进行卷积处理，具体步骤为：首先读入图片得到其像素矩阵.其次，选用不同类型滤波器卷积核并定义卷积核大小.最后，对每一像素点，将其邻域像素与滤波器矩阵对应的元素做乘积运算，相加后作为该像素位置的值.图像滤波公式如公式(7).

图像滤波公式：定义K=O(i,j)为滤波操作，其中(i,j)为像素在图片中的位置，O(·)为滤波操作，K为滤波结果.对(i,j)，给定核函数K(m,n) ((m,n)为卷积核中位置，中心坐标为(0,0))和与核函数对应像素值I(i+m,j+n)，有：

O(i,j)=∑m,nI(i+m,j+n)·K(m,n)

(7)

3 RFSL模型

RFSL模型的总体结构如图1所示，它分为关系网络和融合模型两部分.本节先对两部分内容进行介绍，然后再对RFSL模型进行详细描述.

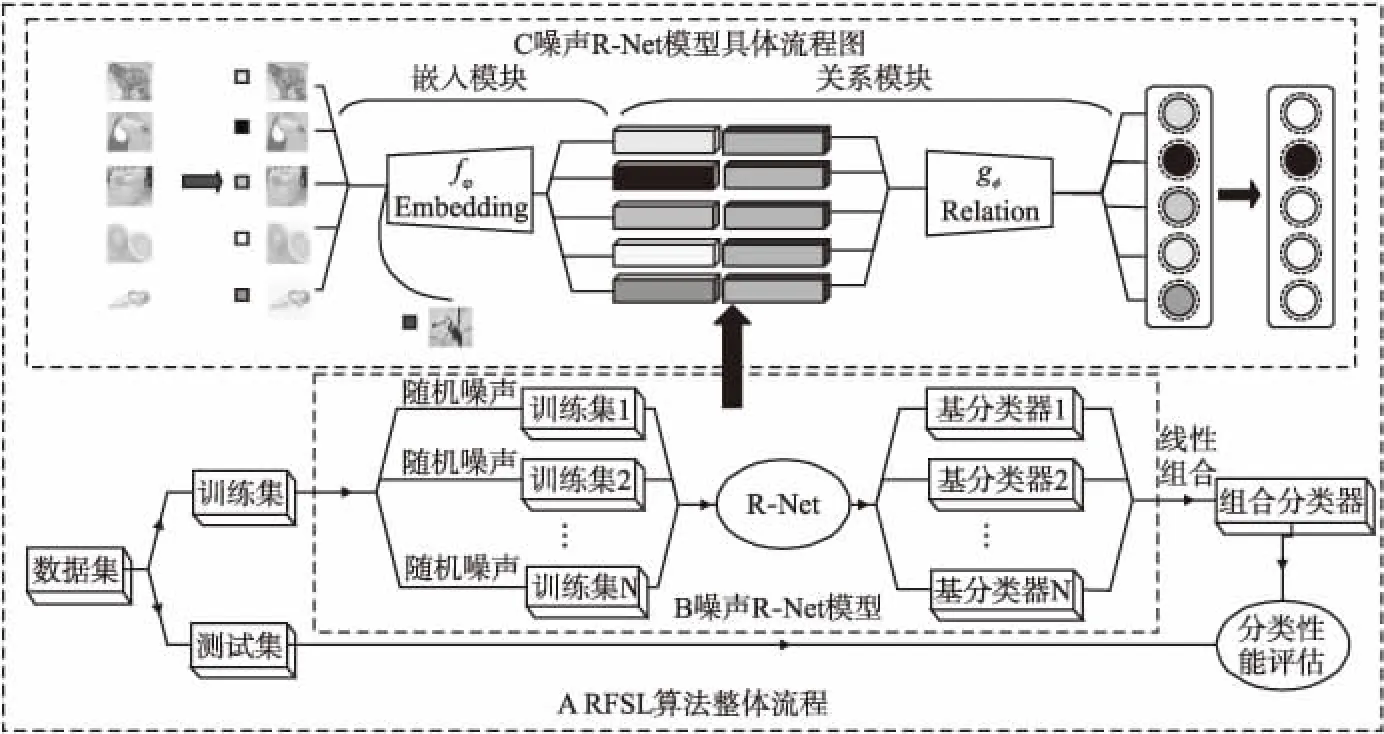
图1 RFSL方法流程图Fig.1 Flow chart of RFSL method

3.1 关系网络

关系网络(R-Net)[14]是一个深度卷积神经模型，其结构包括嵌入模块和关系模块两部分.嵌入模块用于特征提取，包含四个卷积层，前两个卷积层后会有一个池化层；关系模块用于度量图片相似度，包含两层卷积和两层全连接，每个卷积层后会有一个池化层.网络中卷积层均为64个3×3的滤波器，池化层均为2×2的最大池化.

嵌入模块fφ和关系模块gφ，具体网络如图2所示.Xi,Xj分别位于支持集Str和查询集Qtr中，Xi,Xj输入嵌入模块fφ，形成两个特征映射fφ(Xi),fφ(Xj)，然后通过算子C(fφ(Xi),fφ(Xj))结合，C(·,·)为串联方式.将组合算子C(fφ(Xi),fφ(Xj))输入关系模块gφ，计算两特征的相似度，形成0到1范围内的标量，即关系分数.一个输入的支持集样本Xi和查询集样本Xj形成一个关系得分ηi,j，关系得分如公式(8).

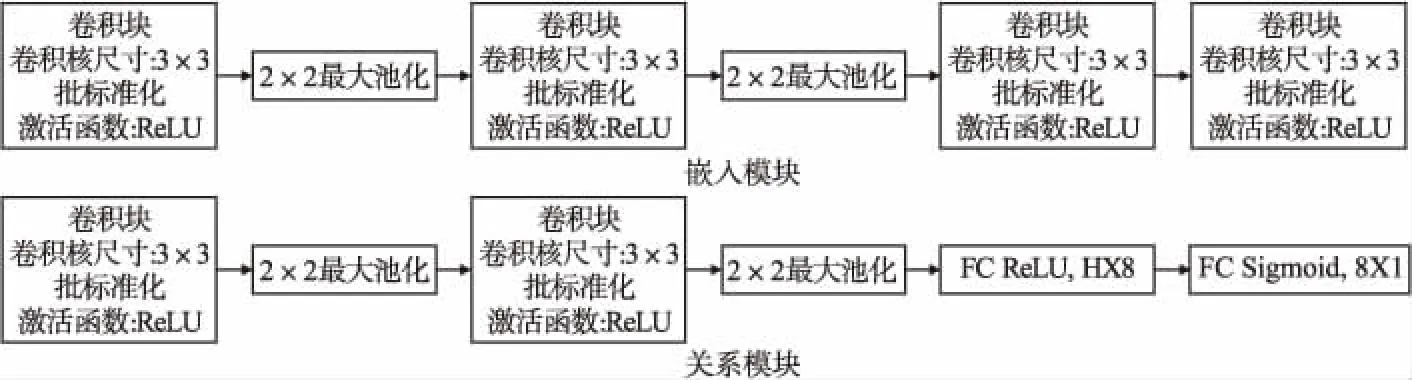
图2 嵌入模块与关系模块网络结构图Fig.2 Network structure of embedded module and relationship module

ηi,j=gφ(C(fφ(Xi),fφ(Xj))),i=1,2,…,C

(8)

目标函数使用均方误差(Mean Square Error,MSE)损失和梯度下降训练模型，将关系得分ηi,j结果进行独热编码：匹配对相似度为1，不匹配相似度为0，均方误差损失函数如公式(9).

(9)

3.2 融合深度神经网络

集成学习是利用多个不同的基学习器解决同一任务，从而提高模型的泛化能力[19].集成算法需要解决的两个问题：一是如何构建具有差异性的基学习器；二是如何进行学习器的融合.结合少样本学习算法对数据敏感的特性，利用随机噪声技术训练了一种鲁棒性的少样本学习模型.

具体训练策略见3.3算法1.模型采用2.3节中核密度估计与图像滤波方法添加随机噪声.在实验中，做了同核不同参数的Gaussian核函数及不同参数的bilateralFilter对图像进行双边滤波，发现参数的调整对实验准确度和融合效果整体影响较小，因此选用多种类型核函数以及其他不同类型噪声参与训练，主要包括：Gaussian、bilateralFilter、poisson、salt、pepper、salt&pepper、spakle、pepper、blur、localvar、sharpening等.

融合阶段：RFSL对基分类器最末的Sigmoid层结果采用相对多数投票法(Plurality Voting).具体做法：首先，将多个基分类器关系模块结果的关系得分η相加，得到多基分类器Sigmoid层结合结果.然后，选择后验概率相对最大的类别结果作为最终结果.相对多数投票法公式如公式(10).

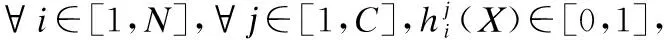
(10)

3.3 RFSL算法

算法1：RFSL训练策略.C为分类种类，K为每类所取样本个数，N为集成规模，Times为训练次数， 为损失函数收敛阈值.

输入：数据集D=(X,Y,f)，参数C、K、N、Times、θ.

输出：少样本模型Ω′.

Step 1.根据定义1，划分数据集D为训练集Ds、测试集Dt；

Step 2.For i=1 To N

2.2.For j=1To|Xs|

2.2.1.Xij=random_noise(Xij) //为训练集图片加入随机噪声

End For

2.3.建立并行线程Modeli，并行训练(2.4-2.13)；

2.4.weight_init(Ω)

2.5.根据定义2，随机划分Ds为支持集Str和查询集Qtr；

2.6.While(Times>0)

2.7.随机选取支持集Str中实例XS，输入Ω的嵌入模块.按图2结构计算XS特征ξ1：

2.7.1.out=ReLU(Xa⊗H1)

2.7.2.out=MAP(out,H2)

2.7.3.out=ReLU(out⊗H3)

2.7.4.out=MAP(out,H4)

2.7.5.out=ReLU(out⊗H5)

2.7.6.out=ReLU(out⊗H6)

2.8.随机选取查询集Qtr中实例XQ，输入Ω的嵌入模块.按图2结构计算XQ特征ξ2；

2.9.拼接为联合特征矩阵ξ，输入Ω的关系模块.按图2结构计算样本集实例与查询集实例相似度η：

2.9.1.out=ReLU(Xa⊗H7)

2.9.2.out=MAP(out,H8)

2.9.3.out=ReLU(out⊗H9)

2.9.4.out=MAP(out,H10)

2.9.5.temp=ReLU(temp·W1)

2.9.6.η=Sigmoid(temp·W2)

2.10.η为一高维矩阵，每行中每一元素表示样本实例与查询实例相似度，取每行最大相似度所对应标签类别为该样本实例预测标签，记样本实例预测标签为Y′，真实标签为YQ；

2.11.loss=MSE(YQ,Y′)；//采用均方误差作为关系网络损失函数.

2.12.If(Time>0‖MSE(Y,Y′)>0)

2.12.1.Times=Times-1

2.12.2.利用梯度下降反向传播loss值，调整Ω参数；

End If

2.13.输出当前模型Ωi；

End For

Step 3.采用投票模型，融合基网络模型Ω1,Ω2,…,ΩN，得最终少样本模型Ω′；

Step 4.输出少样本模型Ω′，算法停止.

4 实验及结果分析

为了RFSL方法的效果，实验分为三个部分，即实验1、实验2和实验3.实验1将RFSL和现有主流少样本学习方法的分类效果进行对比；实验2分析了RFSL分类效果与集成规模N之间的关系；实验3是探究随机噪声对R-Net模型的性能影响以及异构有效性的分析.

数据集：miniImageNet[20]和Omniglot[21]是研究少样本学习算法的两个经典的公开数据集.miniImageNet数据集最初由Oriol Vinyals等人提出，由60000张彩色图片组成，包含100个类，每个类包含600个示例，每个类之间的分步差异性很大.Omniglot数据集包含来自50种不同字母的1623个不同手写字符(类)，每个字符(类)包含由不同人绘制的20个样本.

实验方法：对于miniImageNet数据集，我们按照文献[14]提出的拆分规则，将其分为64个、16个和20个类进行训练、验证和测试，16个验证集用于检验模型的泛化性能.实验中，随机噪声在训练集加入，验证集和测试集保持与对比模型相同.对Omniglot数据集，使用1200个原始类别加旋转和随机噪声进行训练，其余423个类加旋转保持与对比实验相同进行测试.

设置：随机选取C个类，每个类选取K个样本作为支持集，剩余样本选择q作为查询集，支持集与查询集见定义2、3.对于miniImageNet数据集，除了K个样本，5-way 1-shot包含15张查询图片，5-way 5-shot包含10张查询图片.例如，5-way 1-shot每个训练批次共需15×5+1×5=80张图片.对于Omniglot数据集，除了K个样本， 5-way 1-shot包含19张查询图片，5-way 5-shot包含15张查询图片，20-way 1-shot包含10张查询图片，20-way 5-shot需要5张查询图片.例如，5-way 1-shot需19×5+1×5=100张图片.

本文实验采用的硬件环境为NVIDIA Tesla K80 GPU显卡；软件环境为Linux系统、Python语言和Pytorch深度学习框架.

4.1 实验1：RFSL方法分类效果验证

实验1的主要目的是测试RFSL方法的分类效果并与现有的少样本学习方法进行了对比.具体参数的设置保持与文献[14]相同，分C=5，K=1和C=5，K=5进行训练并做对比实验.同时，对Omniglot数据集增加分类难度更高的C=20，K=1和C=20，K=5两对比实验.

实验步骤如下：

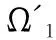
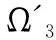
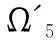
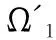
miniImagentNet和Omniglot数据集的分类具体对比实验结果分别如表1、表2所示.

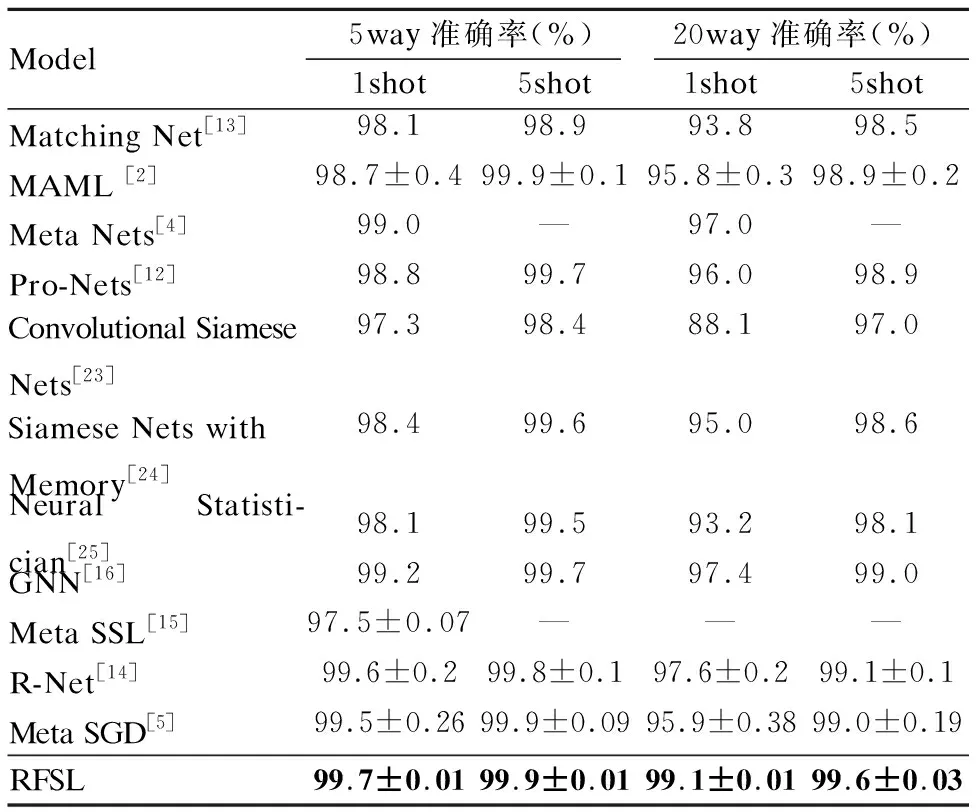
表1 Omniglot数据集下RFSL方法与目前主流少样本学习方法准确率对比Table 1 Comparison of the accuracy of RFSL method and the current mainstream Few-Shot learning method in Omniglot dataset

从表1中可以看出，对于Omniglot数据集，在C=5，K=1；C=5，K=5；C=20，K=1；C=20，K=5参数设置下，RFSL方法均达到了99%以上的准确率，且均超过其他主流的少样本算法.尤其是在难度较高的C=20，K=1参数设置下，RFSL方法准确率也能达到99.1±0.01%，比目前最好的R-Net高出约2个百分点.这说明RFSL在面对灰度图的新域时，表现出了较好的准确率和泛化性.

miniImagentNet数据集分布差异较大，是检验少样本分类器性能的重要标准数据集.从表2中可以看出，C=5，K=1设置下，模型准确率达到了(53.52±0.11)%，比R-Net(50.44±0.82%)准确率高出3个百分点，且分类准确率超出现有主流的其他少样本方法；C=5，K=5设置下，模型准确率达到了(69.54±0.31)%，比R-Net(65.32 ± 0.70)%准确率高出4个百分点，同样超出现有主流的其他少样本方法.实验结果表明，RFSL在数据集分布差别较大的miniImagentNet数据集上，取得了比目前主流分类器较好的分类性能.同时，结合表1、表2还可以看出，RFSL模型的标准差较小，说明分类结果离散度更小，分类性能更稳定，面对新域时泛化性能更好.

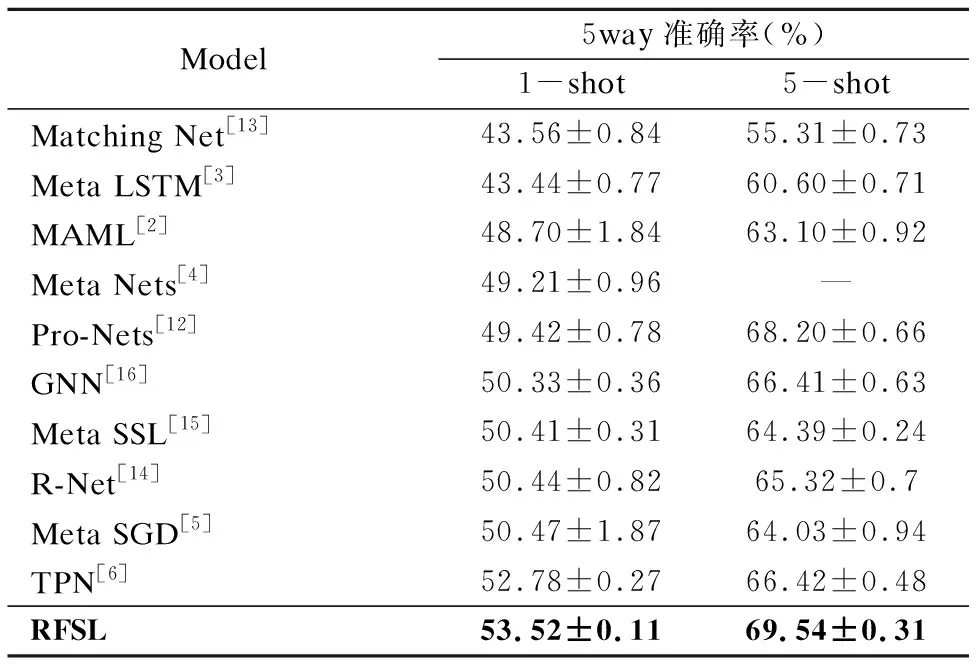
表2 miniImageNet 数据集下RFSL方法与目前主流少样本学习方法准确率对比Table 2 Comparison of the accuracy of RFSL method and the current mainstream Few-Shot learning method in miniImageNet dataset

4.2 实验2：RFSL分类效果与集成规模N的关系

实验2的主要目的是为了研究RFSL分类效果与集成规模N的关系.从表1中可以看出在Omniglot数据集下，RFSL的准确度提升空间较小，效果不明显.因此，我们在miniImageNet数据集上来研究RFSL分类效果与集成规模N的关系，将N从1依次增加到10，分别在C=5，K=1和C=5，K=5设置下的实验结果进行对比.

实验步骤如下：

Step 1.For i=1 To 10

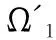
1.2取N=i ，C=5，Times=500000

1.2.1.if(N=1)跳过算法1步骤2.2

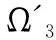
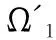
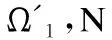
图3 RFSL分类效果与集成规模N的关系Fig.3 Relationship between RFSL classification effect and integration scale N

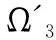
4.3 实验3：噪声对模型性能的影响分析

实验3的目的是为了探究随机噪声对R-Net模型的性能影响以及分类器异构有效性的分析，实验对比了添加高斯噪声前后，模型在Omniglot和miniImageNet数据集的5-way 1-shot和5-way 5-shot实验中训练集损失函数值和支持集错误率的变化情况，模型迭代次数为70000次，前100次变化率较大，每20次记录一次，以后每迭代200次记录一次结果.

实验步骤如下：

Step 1.按照算法1的实验步骤，取C=5，K=1和5，Times=70000

1.2.输出并保存损失值

1.4.输出并保存损失值

Step 2.计算支持集错误率

2.2.输出并保存错误率

2.4.输出并保存错误率

实验记录添加高斯噪声前后实验损失函数值和错误率结果，未添加噪声的实验运行时跳过算法1的步骤2.2继续运行.

实验结果如图4～图7所示.

图4～图7主要包括Omniglot数据集和miniImageNet数据集上5-way 1-shot和5-way 5-shot实验训练损失函数值和支持集测试错误率的拟合结果，“RFSL 5-way 1-shot”和“RFSL 5-way 1-shot”为训练时添加gaussian噪声的结果.

1)对于Omniglot数据集，从图4～图5可以看出，加入噪声对模型的损失和准确度影响并不大，在两实验上模型损失变化率和错误率的变化情况以及收敛情况基本一致.且随着迭代次数的增加，准确度均能达到99%以上，说明在分布差异较小的Omniglot数据集上，噪声对模型收敛和准确度影响较小.在20-way实验中，损失函数值和错误率拟合结果与5-way差别不大，噪声对模型收敛和准确度影响也较小，因此不再对其做图表展示.

图4 RFSL添加噪声前后在Omniglot数据集上5-way 1-shot的损失函数值和测试错误率Fig.4 Loss function value and test error rate of 5-way 1-shot on omniglot dataset before and after adding noise

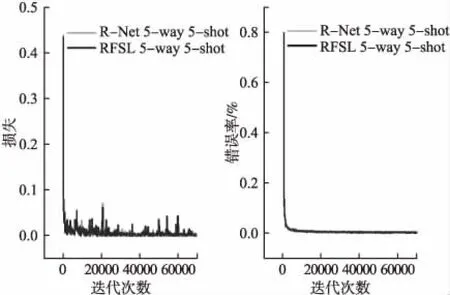
图5 RFSL添加噪声前后在Omniglot数据集上5-way 5-shot的损失函数值和测试错误率Fig.5 Loss function value and test error rate of 5-way 5-shot on Omniglot dataset before and after adding noise

2)对于分布差异大的miniImageNet数据集，噪声对模型的影响比较明显，如图6～图7所示，噪声对5-way 1-shot和5-way 5-shot实验均呈现提前收敛的趋势；对于5-way 1-shot实验，加入高斯噪声后损失函数值比未添加噪声的模型高0.01左右，模型平均准确率为46.8%，比未添加噪声的模型低3%左右；而对于5-way 5-shot实验，加入高斯噪声后损失函数值比未添加噪声的模型高0.02左右，模型平均准确率为61.8%，同样比未添加噪声的模型低3%左右.结合实验1模型分类准确率和离散度情况可以得出，噪声有助于模型更快收敛，提早达到较好分类准确率.噪声的扰动会模糊目标特征，减弱源域迁移到目标域的过拟合，使得单个模型的损失略微升高，影响模型分类的准确度，但有利于形成与原模型异构的更适于小样本学习的基分类器.

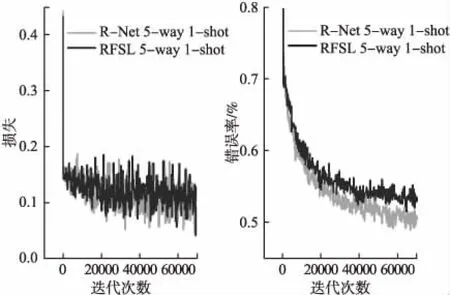
图6 RFSL添加噪声前后在miniImageNet数据集上5-way 1-shot的损失函数值和测试错误率Fig.6 Loss function value and test error rate of 5-way 1-shot on miniImageNet dataset before and after adding noise

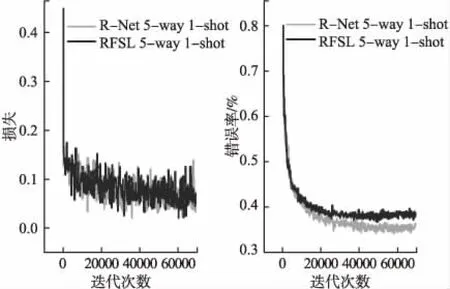
图7 RFSL添加噪声前后在miniImageNet数据集上5-way 5-shot的损失函数值和测试错误率Fig.7 Loss function value and test error rate of 5-way 5-shot on miniImageNet dataset before and after adding noise

5 结 论

近几年，少样本学习的研究热度逐渐上升，它可在较少的标记样本中学习出识别率较好的学习模型.但现有少样本学习算法在源域和目标域分布差异较大的情况下，模型泛化能力较差.且在噪声环境中，面对新域的特征提取能力和泛化能力弱等问题.本文用形式化数学定义方法系统地描述了少样本学习相关概念，运用随机噪声技术训练出不同类型噪声下的异构基分类器，提出RFSL的少样本学习算法，并与现有主流少样本学习算法进行实验对比，结果表明，RFSL模型可促进小样本学习快速收敛，并能有效提高模型的分类预测准确率，具有更强的鲁棒性.下一步的工作将考虑将RFSL算法应用于数据标签预测及自动标注上，进而有效减少样本标记所带来的巨大成本.