行星着陆自主导航地形特征综合优化方法

朱圣英，高锡珍,3，崔平远，姚文龙

(1.北京理工大学宇航学院，北京 100081；2.深空自主导航与控制工信部重点实验室，北京 100081；3.北京控制工程研究所，北京 100190)

0 引 言

着陆探测及采样返回是未来深空探测的主要发展方向。未来的小天体及火星探测任务都要求探测器具备在科学价值较高的区域精确定点着陆的能力。而目标天体距离地球较远，通讯时延严重，这就要求探测器具备自主导航的能力。同时，目标天体环境的先验信息不足、环境扰动等不确定性对自主导航系统提出了更高的要求[1]。

目前着陆过程中主要采用基于惯性测量单元IMU航位递推的导航方法，但该方法无法对初始偏差进行修正，且惯性测量单元存在随机漂移和误差，随着时间的累积误差会逐渐扩散，难以满足高精度导航的要求。由于目标天体表面存在大量的角点特征，美国火星探测漫游者利用下降着陆段获取的序列图像，通过帧间图像的角点检测与匹配对着陆器的相对速度进行估计，但该方法没有获得着陆器的绝对位置信息[2]。针对上述单一导航方法存在的不足，Mourikis提出了基于惯性测量和特征点视线信息融合的自主导航方案[3]。着陆器首先通过检测和匹配特征点获取其在天体固连坐标系下的绝对位置，进而完成视觉导航，然后利用惯导递推更新视觉导航采样间隔内的着陆器运动状态信息。此外，陨石具有一致的轮廓和清晰的几何形状，且广泛分布于天体表面，例如月球[4]、火星[5]、Eros小天体[6]、火卫一[7]，可以用于导航定位。基于此，Cui等提出了基于陨石坑曲线特征的着陆器位姿估计方法[8]。行星着陆自主光学导航方案中，导航路标的数量和位置是影响导航精度的重要因素。一般地，导航路标的数量越多，导航精度越高，但现阶段星载计算机运算能力和存储空间有限。此外导航路标复杂多样，因此需要进一步分析利用多类型路标图像特征信息的导航方案精度异同。基于上述问题有必要研究导航路标优化选取方法，以提高行星着陆自主导航精度和运算效率。

因此，本文对行星着陆导航地形特征综合优化方法进行了研究。针对异构形貌特征评价选取问题，首先利用星表地形图像信息建立不同几何特性特征的测量方程，基于Fisher信息矩阵分析导航系统的可观测度和估计误差下限，然后进一步对多类型异构特征进行评价选取，综合对比分析了观测不同类型地形特征对导航方案性能的影响，可实现多类型特征最优利用，提高导航精度。

1 动力学模型

本文暂不考虑姿态动力学，只考虑平动动力学和姿态运动学，则在着陆点坐标系下建立探测器着陆动力学方程为[9]：

(1)

(2)

在下降着陆段，行星转动引起的科氏加速度远小于当地引力加速度和控制加速度，因此可忽略行星自转影响。若不考虑行星自转，探测器着陆动力学方程简化为：

(3)

2 行星着陆光学导航观测模型

光学导航是深空探测的主要导航方法，主要利用导航相机对目标天体或目标天体表面成像，通过图像处理提取导航特征。在探测器着陆过程中，导航系统的观测方案必须包含描述探测器与天体表面控制点之间直接几何关系的测量量，或描述探测器与其它已知导航特征之间间接几何关系的测量量。导航测量量的引入有助于提高自主导航的精度与自主性。在现在发展的行星着陆自主光学导航系统基础上，本节依据导航地形特征几何特性的不同分别给出了行星着陆自主光学导航系统的三种观测方案，并建立了相应的观测模型。值得注意的是本节光学导航观测方案均采用单目相机，且观测模型中导航地形特征绝对位置信息假设已知。

2.1 地形特征观测模型

1)特征点观测模型

特征点作为一种普遍的导航地形特征已成功用于火星着陆导航，如MER探测器的DIMES系统。目前常用的特征点主要包括SIFT特征点、角点和陨石坑中心点三类。导航相机模型采用小孔成像模型，火星表面上的任一导航路标点pj在任一下降着陆图像中检测的特征点测量量为

(4)

中，矢量[uj,vj]T表示特征点在图像坐标系下的像素坐标，f表示相机焦距，Cxj，Cyj和Czj表示路标点pj在相机坐标下位置矢量的三轴分量，满足

(5)

式中:C(q)表示着陆点坐标系到探测器本体坐标系的转换矩阵；Lpj表示路标点pj在着陆点坐标系中的位置矢量。

式(4)表示利用特征点像素信息建立的观测模型。除此之外，测量探测器与图像特征点视线方向可以给出特征点的视线矢量。建立任一特征点pj单位视线矢量的观测模型为

(6)

2)特征直线观测模型

火星表面存在大量的沟壑、山脊等自然形貌，通过图像处理(如Line segment detector，LSD)可提取星表图像中的线段特征用于火星着陆光学导航中[10]。星表图像中的线段特征在图像坐标系下表示为

Jj=αuej+(1-α)usj

(7)

式中:α表示参数变量，满足0≤α≤1，usj和uej分别表示线段Jj的两个端点的像素坐标，满足式(4)。同时，usj和uej分别对应着陆点坐标下空间线段的两个端点Lpsj和Lpej。结合式(4)和式(5)建立任一特征直线观测模型如下：

(8)

(9)

(10)

式中:kl表示特征直线的方向向量。

由式(8)至式(10)可以看出一条特征线可由两个特征点表示，即一条特征线包含了两个特征点的测量信息。则直观上表明单个特征线相对单个特征点包含更多的测量信息。

3)特征曲线观测模型

此外，相对SIFT特征点、角点等特征点来说，陨石坑在着陆点坐标系下的绝对位置信息通过先前观测更易获得，可用于探测器绝对定位。

针对火星着陆导航，假设目标着陆区域为平面，且陨石坑均位于该平面上。任一陨石坑像曲线特征的观测模型为

(11)

由式(11)可以看出观测值为Ej矩阵，为了便于后续导航滤波，式(11)可改写如下形式。

zj=vech(Ej)=Hvec(Ej)

(12)

式中:zj为特征曲线的观测量，且满足zj=[aj,bj,cj,dj,ej,fj]T，aj，bj，cj，dj，ej和fj表示陨石坑像曲线特征方程的系数，vech(·)表示对称矩阵的向量化形式，vec(·)表示任意矩阵的向量化形式，矩阵Η为vech(·)与vec(·)之间的转换矩阵，满足

(13)

(14)

除式(12)所示的利用陨石坑像曲线方程系数作为观测量，还可直接利用陨石坑曲线特征的中心点、长短半轴和长轴倾角作为观测量。根据上文建立的特征点和特征线观测模型得到陨石坑像曲线特征的中心点ucj和长短半轴aj，bj观测量为

(15)

(16)

(17)

陨石坑曲线特征的长轴倾角观测量为

(18)

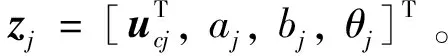
2.2 光学导航系统

为了实现探测器精确着陆，导航系统需要确定探测器在着陆点坐标系下的位置、速度和姿态信息。因此定义导航系统状态如式(19)所示。

x=[LrT,LvT,qT]T

(19)

根据行星着陆动力学模型可得导航系统状态方程如下：

(20)

式中:ac表示探测器本体坐标系下控制加速度，g表示着陆点坐标系下引力加速度，n表示系统噪声，假设其各分量为互不相关的高斯白噪声。

根据导航地形特征不同，特征点、特征直线和特征曲线的观测方程如式(21)～(23)所示。

uj=hu(x)+υu

(21)

lj=hl(x)+υl

(22)

zj=hz(x)+υz

(23)

式中:υu，υl和υz分别表示特征点、特征直线和特征曲线的测量误差，均假设为互不相关的高斯白噪声。

考虑到式(20)～(23)定义的系统状态方程和观测方程均为非线性，可采用EKF等非线性滤波器实现探测器状态估计。

3 基于可观测度分析的导航地形特征综合优化

在2.2节构建的光学导航系统中，导航特征的数量和位置是影响导航性能的重要因素。本节基于可观测度矩阵和Fisher信息矩阵分析导航系统的可观测度和估计误差下限，揭示特征位置和数量与导航系统性能间的关系，在此基础上以导航系统可观测度和估计误差下限为评价指标对随机分布的特征进行优化，综合分析利用不同导航路标特征点，直线和曲线对导航方案性能的影响。

3.1 可观测度分析

对导航系统而言，可观测度揭示了系统通过观测信息确定系统状态的能力。如式(20)～(23)所示的非线性系统，通过线性化方式构建可观测性矩阵，进而分析导航系统的可观测度。

系统状态方程在tk时刻的线性化形式如式(24)所示。

(24)

式中:F表示系统矩阵，其表达式如式(25)所示，G表示控制矩阵。

(25)

(26)

分别线性化特征点、特征直线和特征曲线观测方程如式(27)～(29)所示。

(27)

(28)

(29)

式中:Hu，Hl和Hz分别表示三种观测方程雅克比矩阵。雅克比矩阵Hu具体形式如式(30)所示。

(30)

式中:

(31)

同理，根据式(31)中的偏导数分别可得雅克比矩阵Hl和Hz具体形式如式(32)～(33)所示。

(32)

(33)

式中:Hkrj=∂kl/∂Lr，Hkqj=∂kl/∂q。

基于线性系统理论得可观测性矩阵一般形式[11]

O=[HT,(HF)T, …,(HFn-1)T]T

(34)

式中:n表示系统状态维数。

将式(25)与不同特征观测方程的雅克比矩阵代入式(34)可得导航系统可观测性矩阵。为了定量描述系统可观测的程度，以可观测性矩阵的条件数cond(O)来度量可观测度

(35)

式中:σmax和σmin分别表示矩阵OTO的最大和最小奇异值。

在状态方程中，姿态与位置的耦合体现在速度微分方程中，A3×4正是由于这种耦合关系产生的[12]。取式(34)的前两项构建可观性矩阵[HT,(HF)T]T，在构建可观性矩阵时可将A3×4消掉，因此可以解耦分析位置和速度的可观测性。此外，式(35)定义的系统可观测度难以用状态的解析表达式描述，无法直观地分析系统可观测度的影响因素。本节引入Fisher信息矩阵分析状态可观测性，解析推导系统可观测度。Fisher信息矩阵是观测值所能提供的关于待估状态的信息量期望值的一种度量[13]，F(x)为Fisher信息矩阵，定义为：

(36)

式中:x为系统标称状态，p(Y|x)表示观测量的联合概率密度函数，定义如下：

(37)

式中:σ表示观测噪声标准差，假设不同特征的测量精度相同，下标i表示针对第i个特征点的观测矢量，下标j表示第i个观测矢量的第j个分量。

联合式(36)和式(37)，Fisher信息矩阵进一步推导为

(38)

Cramér-Rao描述待估状态估计量方差的公共下界。结合Fisher信息阵，估计误差方差阵P的迹满足如下不等式：

(39)

式中:λi表示Fisher信息矩阵的特征值。从式(39)可以看出，Fisher信息矩阵的特征值可以评价导航估计误差的大小，同时反映系统可观测性，即特征值越大估计误差越小，系统可观测性越强。因此可采用Fisher信息矩阵的行列式定量衡量系统可观测度大小。下文将基于Fisher信息矩阵分析系统利用不同导航特征的可观测性，进而对导航特征的位置、大小、类型选取进行综合优化。

3.2 单一地形特征分布优化

通过上述分析可知探测器位置和速度的可观测性可以进行解耦分析，同时观测方程中不包含探测器速度信息，因此本节主要分析探测器位置可观测性，进而综合优化导航特征。

1)特征点

结合式(30)，求得特征点观测量关于探测器位置的Fisher信息矩阵为

(40)

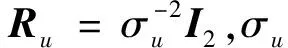
当观测的路标点个数为n时，假设不同路标点在相机坐标系Cz方向上的坐标分量近似相等，即满足Cz1≈…≈Czn=Cz，则探测器位置的Fisher信息矩阵为

(41)

当n≥2时，

(42)

行列式大于零，表明该系统在已知姿态矩阵C时可观测。

当n≥4时，

(43)

式中:

当n≥4时，2(n-2)/n≥1，则有如下不等式

(44)

根据Cramér-Rao界和Fisher信息矩阵，结合旋转矩阵性质可以计算n个特征点情况下的探测器位置估计误差下限为

(45)

当探测器高度一定时，式(45)表明探测器位置估计误差下限与特征点数量和位置有关。探测器位置估计误差下限随特征点数量增加而减小。另一方面，图像坐标系下特征点距图像中心越远，探测器位置估计误差下限越小。因此，考虑到星载机计算资源有限，观测方案中优选距图像中心较远的特征点。

2)特征直线

单条特征直线观测量关于探测器位置的Fisher信息矩阵为

(46)

式中:σl表示特征直线观测噪声标准差，Γuej和Γkj表达式如式(47)和(48)所示。

(47)

(48)

同样地，由式(46)可知系统可观测度随特征直线数量的增多逐渐增强。观测n条特征直线时探测器位置估计误差下限为

(49)

可以看出探测器位置估计误差下限不仅与特征直线数量还与其位置和长度有关。图像坐标系下特征直线端点距图像中心越远，直线段越长，探测器位置估计误差下限越小。

3)特征曲线

同理，推导单条特征曲线观测量关于探测器位置的Fisher信息矩阵为

(50)

式中:σz表示特征曲线中心点和长短轴观测噪声标准差，σθ表示特征曲线倾角观测噪声标准差，Γuej和Γkj表达式如式(51)和(52)所示。

(51)

(52)

(53)

Γθj=03×3

(54)

从特征曲线的Fisher信息矩阵中可以看出，系统可观测度只与特征曲线的位置和大小有关，而与特征曲线倾角无关。

观测n条特征曲线时探测器位置估计误差下限为

(55)

通过式(55)可知，图像坐标系下特征曲线中心距图像中心越远，特征曲线长短轴越长，探测器位置估计误差下限越小。

3.3 异构地形特征类型筛选

通过对比分析式(45)和式(49)发现，当特征点位于特征直线段上时，利用特征点作为观测量的系统导航精度相对较低。由特征直线观测模型可知一条直线段由两个端点确定，因此可比较利用一条特征直线和两个特征点的导航方案估计误差下限，以此为评价指标选取最优导航特征。上述两种导航方案估计误差下限对比可以通过下式进行分析。

(56)

如果两个特征点图像坐标满足式(56)，通过拟合两个特征点为一条直线可获得更高的导航精度。

针对利用特征点和特征曲线的导航方案，仅利用特征点(如陨石坑中心点)作为观测量导航方案估计误差下限更大，相应的导航精度更低。综合对比利用三类特征导航方案Fisher信息矩阵可知，一条特征曲线的信息量不仅包含一条特征直线的信息，还包括另一条特征直线的长度信息，因此，特征曲线可优选为理想导航特征。下面将通过数值仿真进一步验证相关结论。

4 仿真校验

为了检验光学导航特征优化方案有效性及光学导航可行性，本节在Matlab环境下以火星着陆探测为背景进行数学模拟仿真。设探测器到达着陆点上方100 m处时仿真结束，着陆时间120 s。探测器在着陆点坐标系下的初始状态及状态误差标准差如表1所示。图像处理中特征点、特征直线端点、特征曲线中心点和长短轴图像精度均为1个像素，特征曲线倾斜角精度为倾斜角度的1%。特征曲线图像处理误差如图1所示。三种导航特征绝对位置信息已知，假设其各方向均存在10 m的随机误差。导航相机参数如表2所示。

表1 探测器初始状态参数

图1 曲线特征处理误差

表2 导航相机参数

首先对比分析特征点优选前后探测器导航精度。在上述仿真条件下，分别计算探测器利用优化选取的10个特征点与随机选取的10个特征点导航时的状态估计误差，对比结果如图2所示。

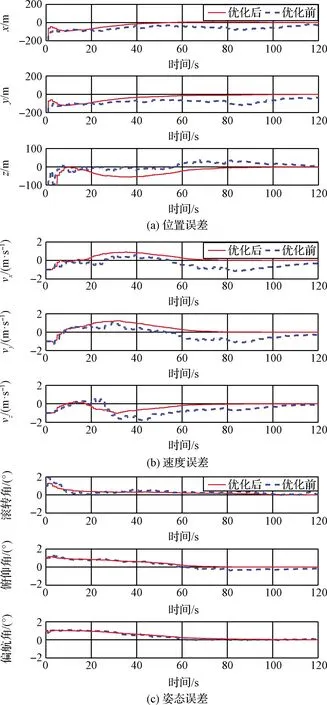
图2 特征点优选前后状态估计误差对比

仿真结果表明探测器利用优化后的特征点导航时，其位置、速度和姿态估计精度均提高，这与3.2节的理论分析一致。式(45)中探测器在本体系下的位置分量远大于图像大小，因此优选后的导航特征并不能大幅提高导航精度，可通过增加导航特征数量来进一步提高导航精度。

然后，分别针对特征直线优化前及优化后的导航方案，采用5条特征直线进行探测器状态估计，探测器各状态估计误差如图3所示。图中探测器位置、速度和姿态估计误差均能较快收敛，表明探测器利用特征直线导航的可行性。同样证明了理论分析的结论，即选择长度较长和距图像中心点较远直线观测量有助于提高导航精度。进一步分析利用特征曲线的导航方案，采用3条特征曲线进行探测器状态估计，探测器各状态估计误差如图4所示。仿真结果与上述一致。以上分析证明了基于Fisher信息矩阵优化导航特征方案的有效性。

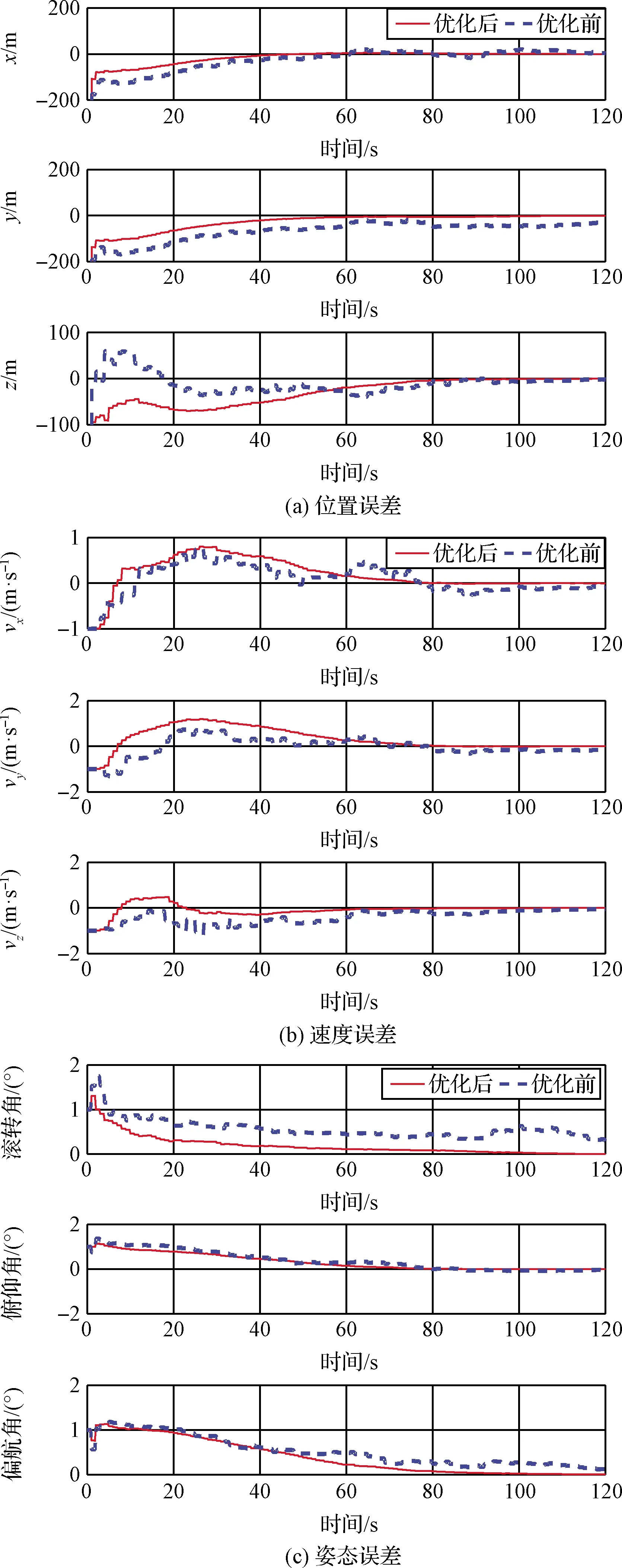
图3 特征直线优选前后状态估计误差对比

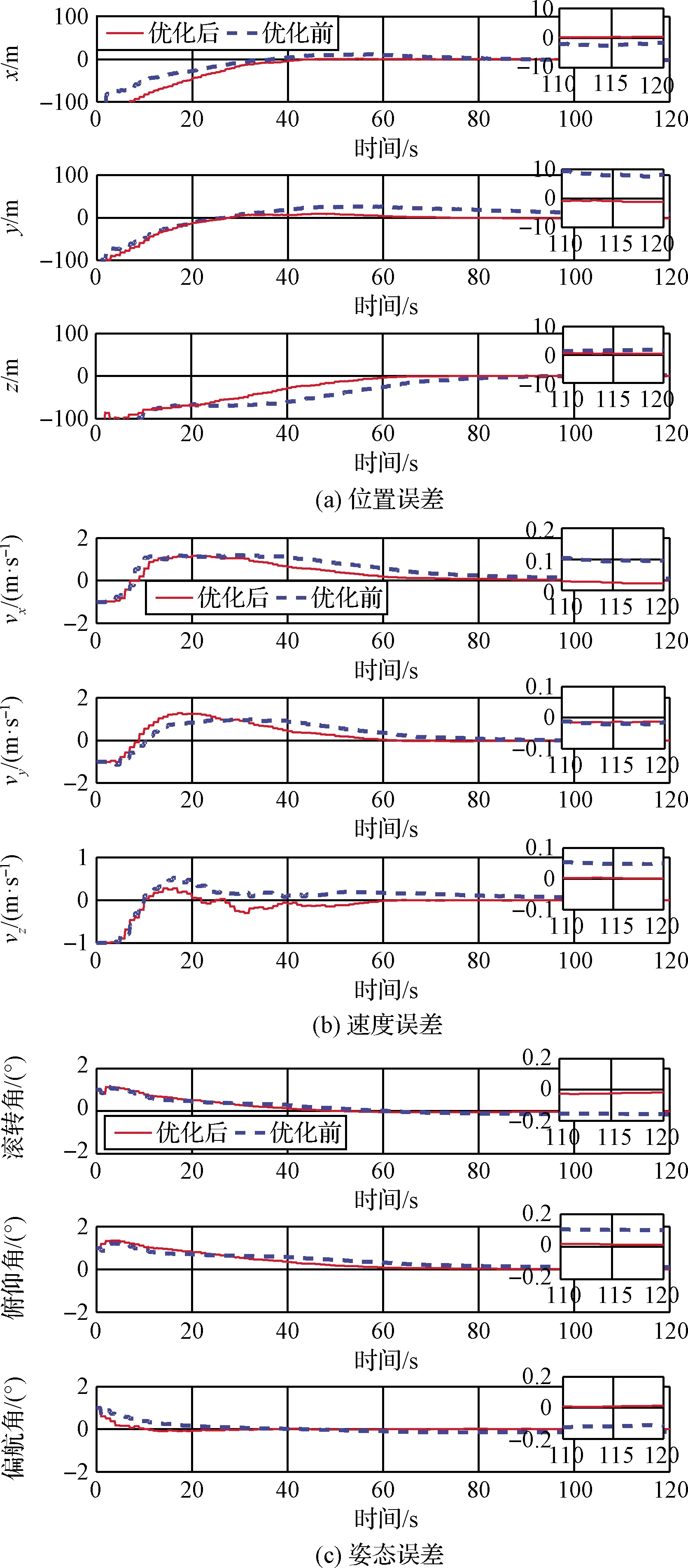
图4 特征曲线优选前后状态估计误差对比

为了综合对比利用不同导航特征的导航方案状态估计精度，分析利用不同导航特征的导航方案优劣性，分别采用3条特征曲线、5条特征直线和10个特征点进行探测器状态估计，探测器各状态估计误差如表3和图5所示。

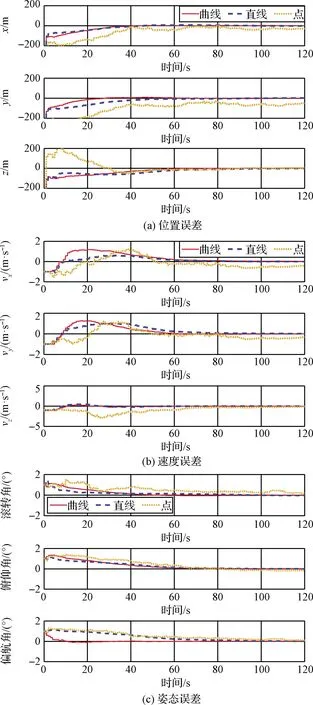
图5 三种导航方案探测器状态估计误差对比

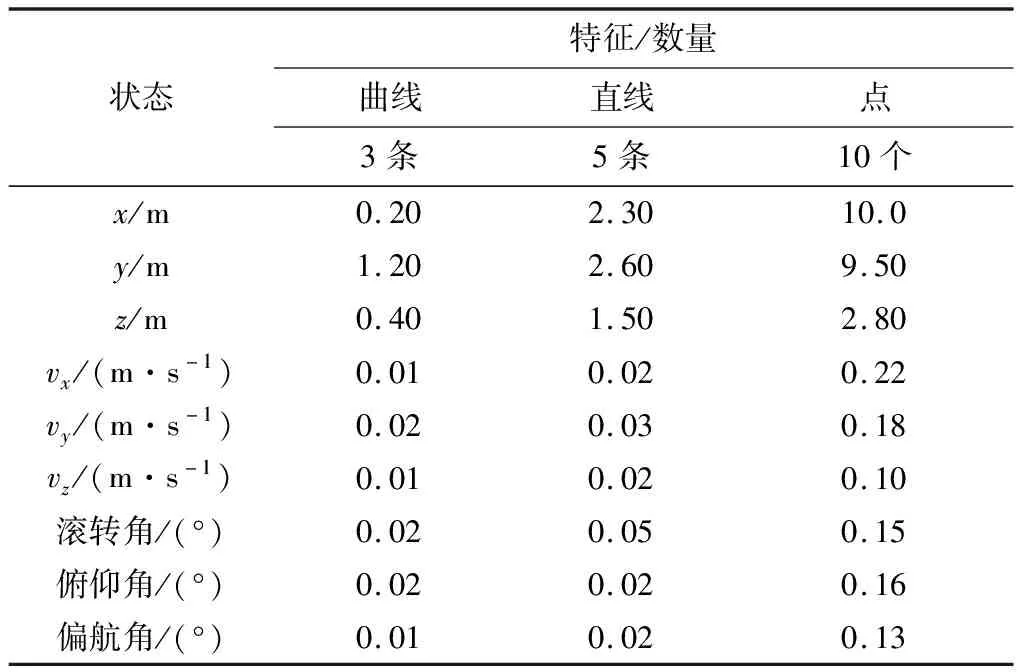
表3 不同导航特征最终时刻平均导航误差

仿真结果表明，采用3条特征曲线进行探测器状态估计，探测器位置和速度估计精度分别优于采用5条特征直线的探测器位置和速度估计精度，探测器姿态估计精度不低于采用5条特征直线的探测器状态估计精度。同时可以发现采用3条特征曲线进行探测器状态估计，探测器各状态估计精度远优于采用10个特征点的探测器状态估计精度。综上对比分析，采用3条特征曲线的探测器状态估计精度最高，采用10个特征点的探测器状态估计精度最低，因此应选用特征曲线设计导航系统，以提高导航精度。

5 结 论

针对多类型复杂形貌特征评价选取问题，提出了基于可观测度的导航地形特征综合优化方法。基于Fisher信息矩阵分析了导航系统的可观测度和估计误差下限，揭示了导航地形特征数量越多，导航估计精度越高。在此基础上以导航系统可观测度和估计误差下限为评价指标对随机分布的特征点、特征直线以及特征曲线形貌路标进行了优化选取。通过仿真对比表明了优化选取方案的正确性，提高了导航精度。