浮子式液位计现场校准装置设计

吴凯，姜璋，李志刚，金荣品

（1. 国防科技工业大容量一级计量站，上海 201203；2. 海军装备部驻上海第一军代表室，上海 201203）

0 前言

浮子式液位计因其精度高、 环境适应性强、安装方便等特点被广泛应用于液面测量领域［1］。目前，液位计检定都是在实验室环境下进行的，由于实验室环境条件与现场环境条件差别大，使用实验室标定的数据不能保证浮子式液位计与现场实际使用的精度一致。 针对此问题，利用高精度传感器结合辅助设备设计出浮子式液位计现场校准装置，确保液位计安装后的精度准确可靠。

1 液位计现场校准装置系统设计

1.1 浮子式液位计的工作原理

浮子式液位计结构如图1 所示，工作时其电路部分将在波导丝上激励出脉冲信号，该信号沿波导丝传播并在波导丝周围产生脉冲磁场，液位计导杆外配有一浮子，浮子可以沿导杆随液位的变化而上下滑动。 在浮子内部有一组永久磁铁。 当脉冲磁场与浮子产生的磁场相遇时，浮子周围的磁场发生改变，产生一个扭转波脉冲，这个脉冲以固定的速度沿波导丝传回并由超声换能器检出。 通过测量脉冲信号与扭转波的时间差可以精确地确定浮子所在的位置，即液面的位置［2］。

图1 浮子式液位计结构图

1.2 浮子式液位计现场校准系统设计

在工作状态下，浮子式液位计可以实时得到液体的高度，要想得到液位计的示值误差，就必须对浮子式液位计进行现场校准，如图2 所示。 浮子式液位计自动检校装置基于光电测量原理，采用精密测距仪作为标准器，机械装置用来提升浮球，模拟浮球在液面上的运动，再结合精密双轴电子补偿器对精密测距仪的距离值进行改正。 这种方法的优点在于可以提高现场计量工作效率，整个测量过程实时连续，避免了以往注水等待时间；另一方面，通过计算机测控系统监测整个测量过程，避免了人工控制的影响，有利于提高测量准确度。

校准方法采用光电测距原理，利用精密测距仪作为主标准管。 使用机械装置提升浮球，满足全量程的检校要求，并结合倾斜补偿器修正测量过程中的倾斜误差。 该系统总体设计框架如图3 所示。

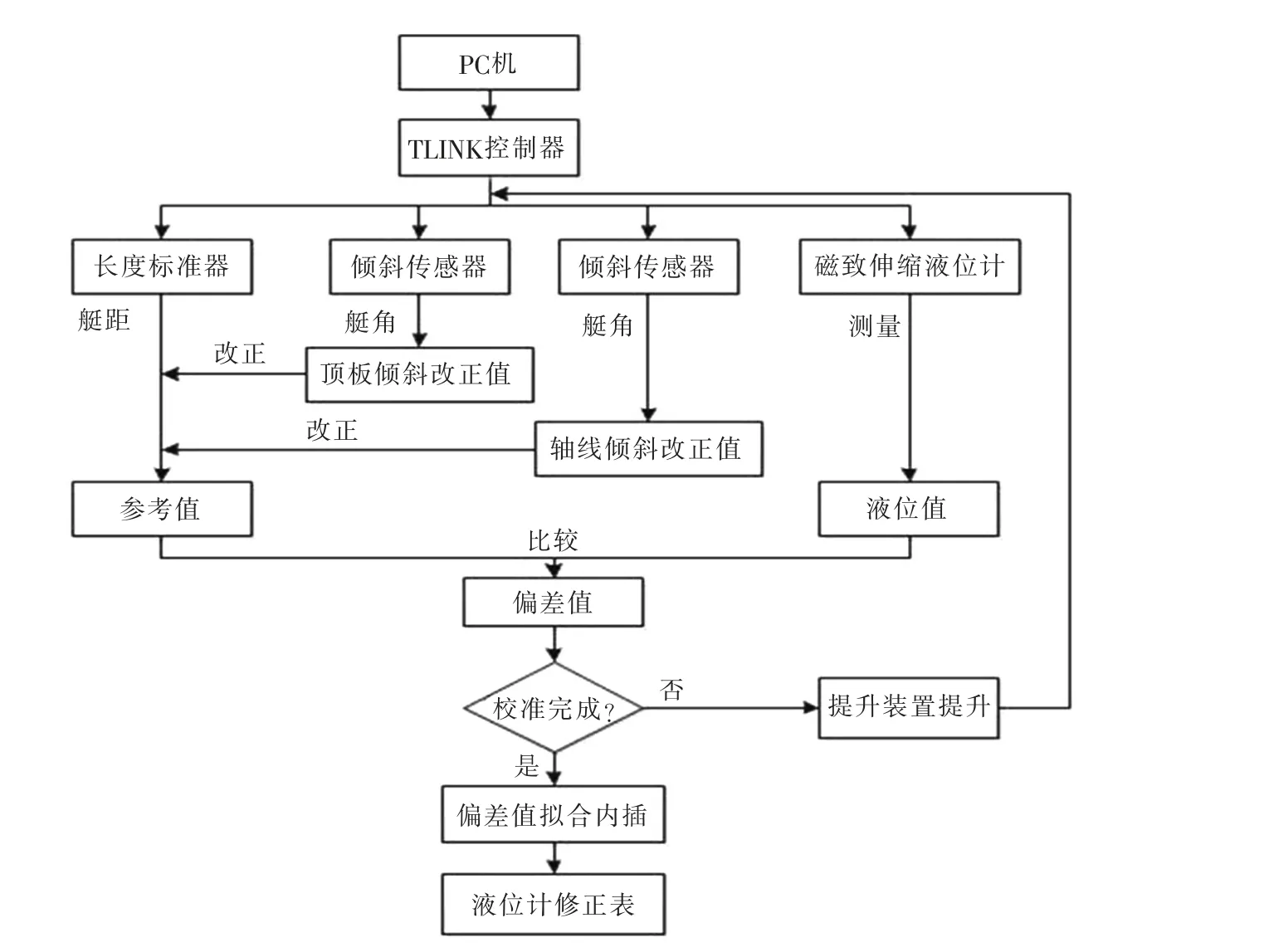
图3 系统总体设计图

浮子式液位计现场校准系统设计原则有以下3个方面：

1） 校准的快速性。 使用精密测距仪、倾斜传感器和机械装置代替传统的钢卷尺、人工注水提升浮球等液位测量设备和方法， 提高实际应用精度，缩短校准时间。

2）校准的准确性。利用精密测距仪作为校准系统的标准器，通过倾斜传感器对长度标准器和提升装置进行倾斜补偿，保证了校准系统的精度。

3）校准的便利性。校准现场多在油罐或者船舱内部，因此要求整个校准装置具有一定的便携性和防爆功能。 系统能实现数据采集和处理自动化，降低人为因素的影响，也能减小现场人员工作量。

1.3 浮子式液位计现场校准装置组成

设计完成的一套便携式现场校准装置， 具有携带便捷、安装方便、稳定性高、操作简单等特点。校准装置中以精密测距仪作为长度基准， 基本原理是通过精密测距仪得到距离参考值， 同时浮子式液位计自身测得液位值， 将距离参考值与液位值进行比对，得到校准结果，实现浮子式液位计的现场校准。

图4 所示为校准装置系统组成示意图。

图4 校准装置系统组成示意图

从图4 可以看出，浮球提升装置通过3 个脚支撑与地面接触， 提升装置中间伸缩杆与地面分离，伸缩杆顶部配有圆水准器，通过调节3 个脚支撑调平圆水准器。 提升装置采用气动提升方式工作，为了防止测量过程中伸缩杆下滑，伸缩杆伸长至一定长度后可以锁死， 避免伸缩杆下滑带来测量偏差。提升装置的加工工艺、伸缩杆之间存在间隙等原因导致顶板在提升过程中会出现小幅度的倾斜，进而导致棱镜在垂直方向出现移动，带来测量偏差。 为了补偿顶板倾斜带来的偏差，在棱镜上方安置1 台倾斜补偿器，实时测量顶板与水平面的夹角，通过棱镜与浮球中心的距离求出偏差值，对精密测距仪的测距值进行改正。

浮球在液面上的运动方向为铅垂线方向，因此， 精密测距仪的测距轴线方向也应为铅垂线方向。 精密测距仪的安装误差和平移基座的制造误差等原因导致测距轴线与铅垂线不平行，为了补偿该偏差带来的影响， 测距仪内置1 台倾斜补偿器，实时测量测距轴线的倾斜角，将测距值归算至铅垂线方向。 由于顶板的倾斜导致在校准过程中测距仪不能精确照准棱镜中心， 在测距仪底部安装平移基座，通过调节基座使测距仪精确照准棱镜中心。 通过摄像机实时采集测距仪激光点与棱镜中心的重合度，实现了照准的可视化。 该系统PC 端通过测量软件实现对各个仪器的指令发送和数据采集，软件对采集的数据进行实时显示并存入数据库。 系统采集的数据有距离值、液位值、角度值和温度值，测量软件通过多源数据的联合平差解算，求得液位值与参考值的偏差值，最后对液位值和偏差值进行拟合和内插，得到液位计在全量程范围内的修正值并输出修正表。

2 实验验证

液位计在使用过程中由于测试环境、装置调整以及人为操作影响会产生系统误差，在精度分析前需排除系统误差影响。 在数据重复测量过程中，如有个别数据与其他的有明显差异，则其中可能含有粗大误差，要对其进行正确判断和处理，获得客观测量数据。 确定多个有效测量数据后，可以对浮子式液位计进行精度分析并计算其不确定度。

现场测试对液位计进行浮球上行和下行测试，测试数据如表1 所示。

表1 现场测试数据

2.1 系统误差判别

用不同公式计算标准差，比较判断测量数据是否存在系统误差。 按照贝塞尔公式计算误差σ1，见式（1）。

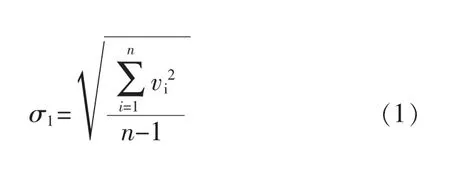
式中：vi为残差，vi=xi-；n 为自由度。

按照别捷尔斯公式计算误差σ2，见式（2）。

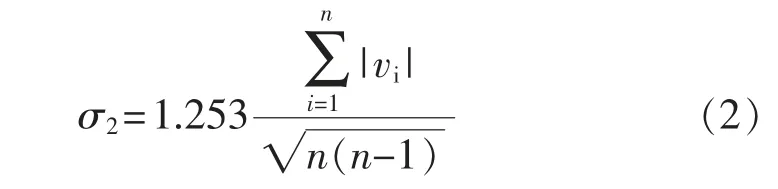
式中：vi为残差为自由度。

2.2 粗差判别

按照3σ（莱以特准则）对粗差进行判断和剔除，需比较Δmax和3σ 的大小，｜。 实验数据中，Δmax=0.78，σ1=0.444，3σ1=1.33，Δmax＜3σ1， 所以无粗差。

2.3 精度分析

该系统以精密测距值作为液位计参考值， 故通过均方根误差（root mean square error，RMSE）评定系统精度，经计算得RMSE=0.444 mm，液位计测试精度满足其标称精度。 通过对精度为±1 mm 的浮子式液位计进行现场校准试验， 验证了校准系统的稳定性和可靠性。

2.4 不确定度分析

测量不确定度是指对测量结果不能肯定的程度，它反映了被测量“真值”的不足。 经测量，合理地赋予被测量的值不是唯一的， 而是有许多个可能的值，“真值”在何处并不知道，只可能获知一个最佳估计值，而“真值”是在最佳估计值的一个不确定度范围内。 这就需要考虑众多分量对测量结果分散的总的影响，从以下几方面因素进行分析：

2.4.1 精密激光测距仪上的读数引起的不确定度分量

精密激光测距仪的测距精度达到±（200 μm +0.2 μm/m），按最大测距6 m 计算，则精密激光测距仪的测距精度为±0.2012 mm。 当已知xi估计值在（b-～b+）范围内概率分布，可由已知的或假设的概率分布确定包含因子k。ui=（b+-b-）/2k。假设其服从均匀分布（下同）， 则此不确定分量u1=0.2012/=0.116 mm。

2.4.2 双轴倾斜补偿器引起的不确定度分量

双轴倾斜补偿器的测角精度达到±1″，按最大测距6 m 计算， 则双轴倾斜补偿器的测距精度为±0.03 mm。 假设其服从均匀分布，则此不确定分量=0.017 mm。

2.4.3 反射标靶水平度引起的不确定度分量

反射标靶的水平度拟采用自动安平技术，利用自动安平装置进行补偿， 其测角精度达到±1″，按最大测距6 m 计算， 则自动补偿仪的测距精度为±0.03 mm。 假设其服从均匀分布，则此不确定分量=0.017 mm。

2.4.4 常数标定引入的不确定度分量

现场常数标定主要采用高精度的标尺或卡尺，其精度可达到±0.02 mm，服从均匀分布，则此不确定分量=0.012 mm。

2.4.5 浮子测量的阿贝误差引起的不确定度分量

由于测量基准线以铅垂线为基准，测量轴线是沿导杆方向的，两轴线不在同一直线上，不符合阿贝原则，故引起阿贝误差。 由于轴线方向不同，取测量出浮子式液位计浮子与固连装置的接触点到反射板中心的距离L 的误差为±1 mm， 偏置角度误差为±2″，则阿贝误差为0.007 mm。 假设其服从均匀分布，故此不确定分量=0.004 mm。

2.4.6 温度测量引起的不确定度分量

在现场测量过程中，受环境温度的影响，浮子式液位计导杆会发生热胀冷缩现象，在实际测量之前需对环境温度进行测量， 并对最终测量结果修正。

浮子式液位计导杆的热胀冷缩程度与导杆材质有关，在实际应用中，以普通船用钢最为常见；其温度修正公式为

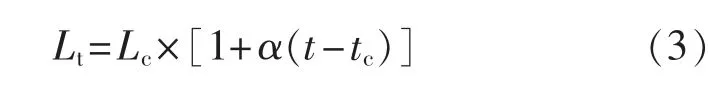
式中：Lt为经温度修正后的导杆长度，m；Lc为浮子式液位计原位检校时的导杆长度，m；t 为实际运用过程中的测量温度，℃；tc为浮子式液位计原位检校时的温度，℃；α 为导杆材料的线膨胀系数，α=0.000012/℃。

ut=t-tc，温度测量不确定度为ut＜0.2℃，则可得长度为6 m 时温度引起的长度测量不确定度分量u6=α×ut×Lc=0.0144 mm。

2.4.7 垂直度引起的不确定度分量

按垂直度的不确定度α 为20′， 浮子式液位计原位检校时的导杆长度L 为6 m 时引起的测量不确定度分量u7=L-Lcosα=0.1 mm。

2.4.8 提升装置不稳定引入的不确定度分量

设提升装置引起的校准误差为±0.2 mm，服从均匀分布，此不确定分量=0.115 mm。

2.4.9 实验数据引入的不确定度分析

表1 数据在测量过程中也会有不确定性，由它引入的不确定度分量也需进行计算，此不确定分量。

因此，合成标准不确定度为

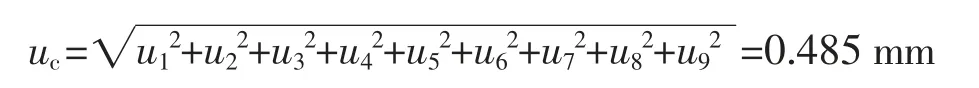
在计量法规中，常用扩展不确定度U 来表示，U 定义为测量结果分散在某区间的半宽度， 也就是该测量结果的标准不确定度的几倍。 这个倍因子又称为包含因子，常用k 表示，由于难以确定被测量值的估计区间及其置信水平，根据国家军用标准规定取k=2， 则扩展不确定度为U=2×0.485 mm=0.97 mm，在浮子式液位计精度范围内。

3 结语

高精度浮子式液位计现场校准装置，应用于国防领域中油库液罐、船舶液舱等液位计现场校准工作，降低了现场校准的难度，提高了工作效率。 文中介绍了浮子式液位计现场校准装置的工作原理和系统组成， 通过分析获取到的现场液位测量数据，验证了该校准装置的可靠性和准确度，能够确保液位计安装后的测量精度满足计量标准，成功研制高精度浮子式液位计现场校准装置，填补了国防领域液位计现场校准的技术空白。