综合管廊燃气舱燃气爆炸冲击波传播特征研究*

夏 微，高 魁,2，乔国栋

(1.安徽理工大学 安全科学与工程学院，安徽 淮南 232001； 2.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室，安徽 淮南 232001)

0 引言

城市地下综合管廊是1种集约式的管线建造模式，其内部综合了给排水、电力、燃气、供热、通信等各种市政管线和设施[1]，并设置专门的检修通道、监测系统，实现市政管线的统一规划、统一设计、统一建设和统一管理[2]，是保障城市运行的重要“生命线”设施[3]。燃气管道进入综合管廊避免了“马路拉链”的现象，但与此同时也带来管道泄漏所造成的一系列新问题。

邓小娇等[4]改变燃气管道管输压力，对燃气泄漏爆炸危险区域进行研究，得到爆炸极限范围移动速度与管输压力成正比。万留杰等[5]研究管廊内燃气浓度分布与泄漏位置的关系。吴建松等[6]研究通风受限空间内的地下综合管廊燃气舱内燃气泄漏扩散规律，结果表明气体射流作用与浮升力作用是影响综合管廊燃气泄漏扩散浓度分布的重要因素。王玉琪等[7]通过改变泄漏孔径、通风速度研究不同工况对燃气扩散的影响。袁欣然等[8]研究泄漏口压力、孔径、朝向等因素对扩散的影响。刘希亮等[9-10]研究管廊内燃气爆炸过程中爆炸冲击波对管廊结构的影响。钱喜玲等[11]研究不同压力条件下的燃气浓度的分布特性。孙加超等[12]模拟综合管廊燃气舱在不同爆炸荷载下的情况，获得管廊的破坏模式、燃气舱内空气中心线各点的超压时程曲线以及超压峰值曲线。燃气舱一旦发生燃气泄漏引发爆炸，在演化传播等系列交互效应中，其传播过程及后果必然会影响到高压电力舱等其他地下综合管廊设施，可能会诱发电缆火灾等次生灾害。田威等[13]通过数值模拟研究燃气舱在1，5，20，40 kg TNT药量下的内爆情况。张凯猛[14]通过数值模拟得出混凝土隔板对防止爆炸冲击具有显著效果，燃气舱受爆炸冲击波影响较大，燃气舱内壁处的超压峰值大于顶板处的超压峰值。刘中宪等[15]得出在燃气爆炸荷载作用下，管廊衬砌的损伤破坏具有局部性和弱传递性。对比高建丰等[16]得出的管道油气爆炸实验结果和Fluent计算模拟结果，发现2者间的误差小于4%。Huang等[17]通过对比管道爆炸的实验结果和数值模拟结果，表明2者的变化规律基本一致。Fluent作为1款流体计算分析软件，其可靠性已经被专家学者验证并得到认可。

文献调研发现，国内学者对综合管廊燃气舱的研究主要集中在燃气泄漏扩散和燃气爆炸对管廊的破坏影响等问题，而对燃气在管廊内爆炸产生的冲击波的传播规律的研究较少。因此本文采用数值模拟的方法，对不同填充长度情况下，管廊燃气舱内燃气爆炸后的冲击波传播特征进行研究，揭示爆炸过程中的压力和气流速度的变化规律。

1 数值模型

针对管廊燃气舱的1个防火分区，采用计算流体力学软件Fluent18.0研究燃气在不同填充长度情况下产生爆炸冲击波的传播特征。简化的物理模型如图1所示，燃气舱断面为1.6 m×2.8 m，防火分区长200 m，两端封闭。沿高为1.4 m的截面中心每隔2 m布置1个测点，共计100个测点，用来监测燃气爆炸过程中产生的超压及气体的水平流速。点火位置位于燃气舱左端。爆炸气体为甲烷-空气混合气体，从燃气舱左端开始填充，填充长度依次为20，50，100，150 m，甲烷体积分数为9.5%。初始温度为300 K，初始压力为101.325 kPa。

图1 管廊燃气舱物理模型Fig.1 Physical model of gas cabin in utility tunnel

为简化计算，对模型做出如下假设：

气体满足理想气体状态；燃气舱墙面为刚性，不考虑流-固耦合作用；系统绝热，与外界无热交换；燃气爆炸过程为单步反应。

2 数值计算结果及分析

2.1 不同填充长度下超压随时间的变化规律

填充长度为20 m时的超压变化如图2所示，由图2可知，随着时间的增加，超压先增大后减小再增大。由于模型封闭端的影响，冲击波传播到右侧时会再次反向传播。

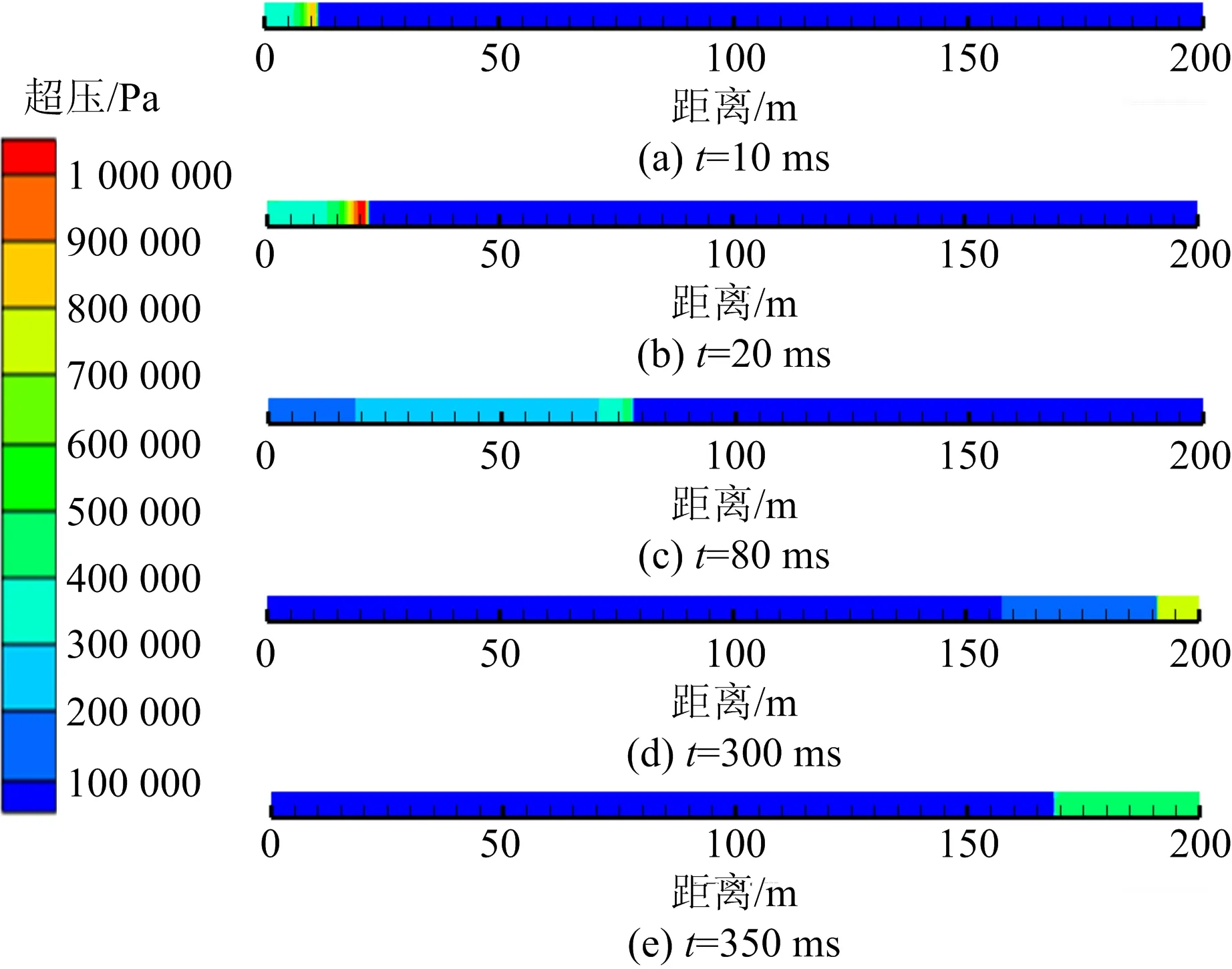
图2 填充长度20 m时超压变化云图Fig.2 Cloud chart of overpressure change when filling length is 20 m

填充长度分别为20，50，100，150 m时，燃气舱内部分测点的超压变化曲线如图3所示。由图3可知，超压随时间的增加呈现出锯齿形状的反复波动，各个测点存在多个超压峰值且2个峰值之间存在明显的时间差。以图3(b)为例说明，甲烷填充长度为50 m，点火之后，燃气舱内形成燃烧波，燃烧波压缩未燃气体形成压缩波，多道压缩波追赶叠加最终形成冲击波。冲击波从点火端开始向外传播，各个测点的超压从左到右依次上升到达第1个峰值；前驱冲击波通过后，超压值下降；随后前驱冲击波后的压缩波到达测点，使得测点的超压值再次小幅上升，之后下降。由于燃气舱防火分区两端封闭，因此当前驱冲击波传播到右侧封闭端时会被反射形成反射波，距离封闭端较近的测点会因冲击波与反射波的叠加作用从而使超压值突跃达到峰值，如图3(b)测点#90。冲击波的反向传播使得各测点超压再次上升，依次到达第2个超压峰值。反射波与火焰压缩波在燃气舱后半段相遇致使超压值突跃到较高的水平，此后压缩波、反射波沿着各自的方向继续传播。压缩波遇到封闭端产生反射，开始向点火端传播。测点#70之后的第2个超压峰值均大于第1个超压峰值。这与冲击波与反射波的叠加作用有关，距离封闭端越近，叠加作用越明显。由于计算模型为封闭绝热系统，产生的能量耗散较少，因此冲击波会在燃气舱内多次反射，出现多个超压峰值。

图3 不同填充长度测点超压变化曲线Fig.3 Change curves of overpressure at measuring points under different filling lengths

对比不同填充长度情况下，发现随着填充长度的增加，冲击波到达各个测点的时间越来越短，超压峰值的下降趋势越来越快。这是由于填充长度越大，燃烧持续的时间越长，燃烧波的存在不断为冲击波的传播提供能量，使得冲击波的传播速度加快。

2.2 不同填充长度下水平流速随时间的变化规律

填充长度为150 m时燃气舱内的水平流速变化如图4所示。由图4可知，燃气爆炸初始阶段，气流水平流速较小，燃气舱前段出现回流现象。160 ms时，在反射波的作用下水平流速开始反向增大。

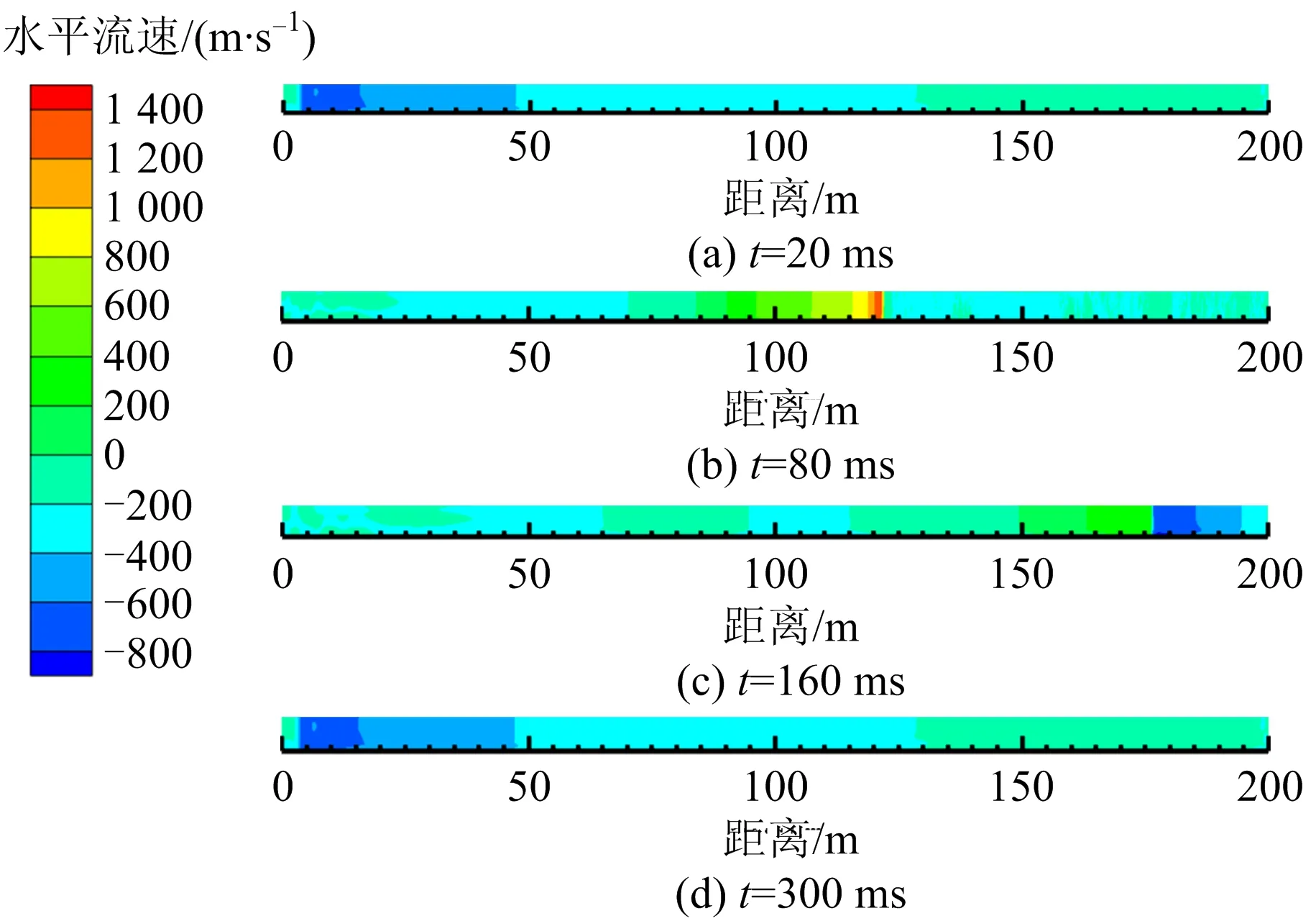
图4 填充长度150 m时水平流速变化云图Fig.4 Cloud chart of flat velocity change when filling length is 150 m

不同填充长度情况下部分测点的水平流速变化曲线如图5所示。由图5可知，水平流速以0为基点在正负区间内上下波动，这是由于模型是封闭空间，气流在封闭端反射波的影响下改变运动方向。以图5(c)为例说明，初始阶段测点处的气流速度会因前驱冲击波的到达上升到第1个流速峰值即首次流速峰值。冲击波过后流速下降，燃气舱前段测点的流速会降到负值，说明前段流场出现了回流。随后火焰压缩波到达测点，流速再次上升。前驱冲击波传播到封闭端发生反射，反射波到达测点处使得流速快速下降，此时流速达到反向峰值。反射波过后，流速减小，反向传播的冲击波传播到点火端继续发生反射，会使测点流速再次上升到正向峰值。由于冲击波会在燃气舱内多次反射，因此测点流速曲线会随着时间的变化上下振荡且正向峰值和反向峰值之间存在明显的时间差。

对比不同填充长度下的流速曲线图，发现随着填充长度的增加，流速正向峰值和反向峰值的时间间隔越来越短。流速峰值的下降趋势也随着填充长度的增加而变快。这与超压的变化趋势是一致的。随着填充长度的增加，燃气舱前段的回流现象越来越明显。

图5 不同填充长度测点水平流速变化曲线Fig.5 Change curves of horizontal flow velocity at measuring points under different filling lengths

2.3 超压峰值和流速峰值变化规律及耦合关系

不同填充长度下的首次超压峰值变化曲线如图6所示。由图6可知，超压峰值随着传播距离的增加总体呈现出先增大再减小再增大的规律。填充长度为100 m和150 m时，超压峰值在第1次增大后不会立刻降低而是保持一段平稳状态。这是由于此时燃气的燃烧速率已达到最大，并保持相对稳定，化学反应产生的能量与冲击波传播过程中损耗的能量趋于平衡。当燃烧反应结束，平衡被打破，因此超压峰值开始衰减。填充长度越大，最大超压峰值越大，对比图中填充长度为20 m和50 m时的曲线能明显看出，填充长度为50 m时的最大超压峰值约为填充长度为20 m时的2倍。图6中50，100，150 m的曲线表明最大超压峰值不会随着填充长度的增加而无限增大，超过某个临界长度后，爆炸超压受填充长度的影响将会变小。由于点火端产生反射波的影响，使得超压峰值在燃气舱前10 m有减小趋势。超压峰值在200 m处发生突跃，是由冲击波和反射波叠加引起的，当填充长度为100 m和150 m时，超压峰值在此处达到最大值，即随着填充长度的增加，产生最大超压峰值的位置由接近填充长度结束的位置转移到燃气舱的封闭端。填充长度为150 m时，封闭端产生的超压约为填充长度结束位置的2.3倍。

图6 首次超压峰值变化曲线Fig.6 Change curves of first peak overpressure

不同填充长度下首次流速峰值的变化曲线如图7所示。由于0 m和200 m处流速为0，所以图7中并未显示。首次流速峰值随着距离的增加总体呈现出先增加再减小的趋势。填充长度为100 m和150 m时，流速峰值会在增加后保持一段平稳状态，流速峰值衰减位置接近填充长度结束的位置。随着填充长度的增大，最大流速峰值先增大后维持稳定。由此可判断燃气舱内存在1个临界填充长度，最大流速峰值达到最大，超过此临界长度，峰值不会再有较大的变化直至衰减。

图7 首次流速峰值变化曲线Fig.7 Change curves of first peak flow velocity

根据上述分析可知首次超压峰值和流速峰值存在一定的耦合关系。不同填充长度下的首次超压峰值与流速峰值的拟合曲线如图8所示。由图8可知，超压峰值与流速峰值呈现为正比关系，即随着首次超压峰值的增大，首次流速峰值相应增大。对比图8中4组方程发现，随着填充长度的增加，方程的斜率减小，截距增大。

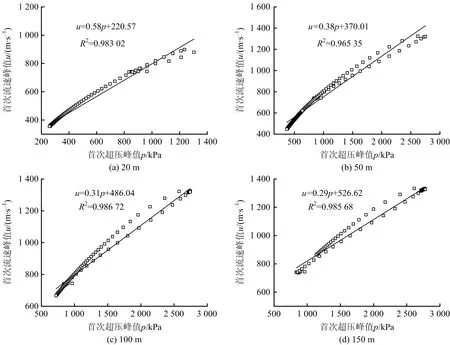
图8 首次流速峰值与首次超压峰值的拟合Fig.8 Fitting of first peak flow velocity and first peak overpressure

流速峰值与超压峰值的关系可表示为u=Ap+B。斜率A和截距B分别与填充长度L拟合所得公式如式(1)～(2)所示：

(1)

(2)

式中：A为斜率；B为截距；L为填充长度，m。

将式(1)～(2)代入u=Ap+B可得首次流速峰值与填充长度和首次超压峰值的关系式，如式(3)所示：

(3)

式中：u为首次流速峰值，m/s；p为首次超压峰值，kPa。

通过数据拟合，建立首次流速峰值与填充长度和首次超压峰值的耦合关系。

3 结论

1)燃气爆炸后，燃气舱内存在多个超压峰值。冲击波到达各测点的时间与燃气填充长度成反比。测点流速曲线随时间的变化以0为基点上下振荡，流速的下降趋势随着填充长度的增加而变快。

2)超压峰值随着传播距离的增加先增大后减小再增大。随着填充长度的增加，产生最大超压峰值的位置由接近填充长度结束的位置转移到燃气舱封闭端，填充长度为150 m时，封闭端产生的超压约为填充长度结束位置的2.3倍。表明在此情况下爆炸产生的超压会对封闭端产生极大破坏，建议在实际设计中对燃气舱防火分区的封闭端进行强化处理。

3)首次流速峰值与首次超压峰值呈现正比关系，流速峰值随着超压峰值的增加而增加。通过拟合得到流速峰值与超压峰值及填充长度的耦合关系，为燃气舱燃气爆炸后的流速分布研究提供参考。