A general thermodynamic model for the long-period stacking ordered phases in magnesium alloys

Kai Xu,Shuhong Liu,Keke Chang,Yongpeng Liang,Yong Du,Zhanpeng Jin

a Key Laboratory of Marine Materials and Related Technologies,Zhejiang Key Laboratory of Marine Materials and Protective Technologies,Ningbo Institute of Materials Technology and Engineering,Chinese Academy of Sciences,Ningbo,Zhejiang 315201,China

bScience and Technology on High Strength Structural Materials Laboratory,Central South University,Changsha,Hunan 410083,China

c School of Materials Science and Engineering,Central South University,Changsha,Hunan 410083,China

Received 19 August 2019;received in revised form 26 December 2019;accepted 30 December 2019

Available online 12 July 2020

Abstract A thermodynamic model Mgx(Xs,Mg)6(Xl,Mg)8(Xs and Xl are elements smaller and larger than Mg)for long-period stacking ordered phases(LPSOs)was proposed based on two key factors:the Xs6Xl8-type L12 clusters and the variation of chemical compositions.In general,all available LPSOs can be described with this model.As a representative system,Mg-Y-Zn with three LPSOs was investigated using the CALPHAD(calculation of phase diagram)approach aided with first-principles calculations.Two new three-phase equilibria were predicted and were validated by key experiments.The model-based descriptions will be the basis for the research and development of magnesium alloys.

Keywords:LPSOs;Thermodynamic model;Formation enthalpy;CALPHAD;Solidification.

1.Introduction

Long-period stacking ordered phases(LPSOs)in magnesium alloys were widely concerned for their remarkable specific strength with moderate ductility[1–5].A series of LPSOs,viz.10H,12R,14H,18R-types[6,7],were observed in Mg-based alloys by different preparation methods and heat treatment processes.Here,H stands the stacking sequence is mirror-symmetrical to the base surface,while R indicates there is no mirror symmetry,and the numbers denote the stacked atomic layers.Hundreds of atoms in each supercell result in the relatively complicated crystal structure[8–10].Various clusters of solute atoms of the LPSOs have been experimentally observed and theoretically modeled.L12cluster is one of the widely accepted models in literature[6–15].In our previous work[16],the chemical compositions of LPSOs in the Mg–Ni–Y system were determined by electron probe microanalyzer(EPMA).The Ni/Y ratio equals to 0.75,which is in line with the L12cluster model.The lattice-distortionmediated HCP-to-FCC structural transformation in the LPSOs was investigated by the atomic array and solute-triplets in the supercell[17].However,the immature thermodynamic description of the LPSOs has misled the phase relations in the Mg-rich region and limited its application in engineering[18–25].Therefore,it is essential to develop a general thermodynamic model to describe the crystal structure and homogeneity region of the LPSOs simultaneously.

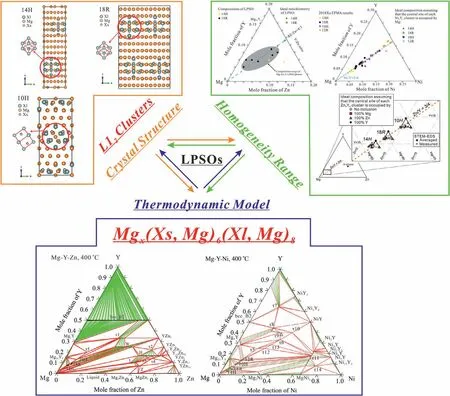
Fig.1.Correlations between the general thermodynamic model Mgx(Xs,Mg)6(Xl,Mg)8 proposed in this work and the crystal structures(Xs6Xl8-type L12 clusters)[6,8,9,13,14,55]and homogeneity ranges[9,14,16]of the LPSOs.

Mg–Y–Zn,as one of the representative LPSOs-containing systems[6,8,9,26,27],was studied in the present work.The 18R phase was formed directly after solidification.It was gradually transformed to the 14H phase during heat treatment in the temperature range of 350–500℃[28–33],where the 24R phase was proposed as an intermediate phase by Kim et al.[6].Hagihara et al.[34]observed a phase transformation from 10H to 18R at around 525℃.But later on,the insufficient annealing time for 10H might lead to the uncertainty of the phase stability[13].Phase relations in the Mg–Y–Zn system were experimentally investigated by several researchers[35–39].Five ternary compounds,viz.X(18R in this work),W,I,H,Z were reported.Thermodynamic evaluation of the Mg–Y–Zn system was also reported several times in literature[18,23–25].In order to reproduce the phase equilibria in the Mg-rich region and the solidification behavior of the Mg–Y–Zn system,an accurate thermodynamic description of the LPSOs is required.

This work aims to develop a general thermodynamic model for the LPSOs.Based on this model,we described the Mg–Y–Zn system using the CALPHAD(calculation of phase diagram)approach supported with first-principles calculations as a typical case.The predicted phase equilibria were then validated by key experiments.

2.Methods

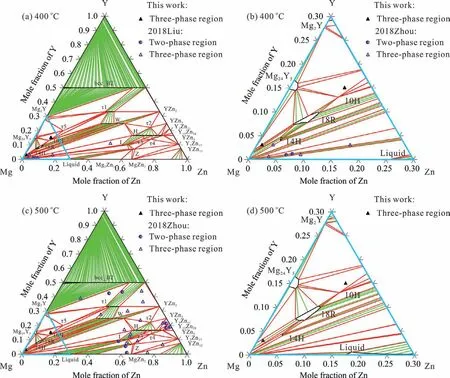
Fig.2.Calculated isothermal sections of the Mg–Y–Zn system with the proposed general thermodynamic model for LPSOs:(a)(c)isothermal sections at 400 and 500℃ with experimental data[37,39];(c)(d)local magnifications in the Mg-rich region,the phase relations are different from the calculations in literature[18,24,25],which have been confirmed by our following experiments in Fig.3.

The total energies of ternary compounds and pure elements Mg,Y,and Zn were performed using the Vienna ab initio simulation package(VASP)[40–42]based on density functional theory(DFT)[43,44].All calculations were performed using the projected augmented wave(PAW)potentials[45]and the generalized gradient approximation(GGA),with the exchange-correlation functional of Perdew–Burke–Ernzerhof(PBE)[46].The electron wave function was expanded using plane waves with a cut off energy of 400eV.The gammacentered k-point mesh generated using the Monkhorst–Pack scheme was used to sample the Brillouin zone.All atoms were fully relaxed until the Hellmann-Feynman forces were smaller than 0.02eV/°A.The energy convergence criterion of electronic self-consistency was 10−6eV/atom.The total energy differences were converged to within 1.0 meV/atom.The formation enthalpies of the LPSOs were obtained with their total energies subtracting the total energies of the pure elements.More details can be found in our previous work[47,48].

The present thermodynamic optimization was carried out by using the PARROT module of the Thermo-Calc software[49].The step-by-step optimization method reported by Du et al.[50]was used in this work.The thermodynamic parameters of pure elements are taken from the SGTEcompilation by Dinsdale[51].The constituent Mg–Zn binary system is taken from Yuan et al.[52].The order–disorder transition models in the Mg–Y and Y–Zn systems have been modified based on the previous work[23,53].With descriptions of the boundary binary systems,phase equilibria and thermodynamic properties in ternary systems can be computed via the standard procedure[54].

Two key alloys Mg96Y3Zn1(at%)and Mg75Y15Zn10(at%)were prepared to verify our calculations.Magnesium granules(99.8wt%,Alfa Aesar),yttrium ingot(99.9wt%,Alfa Aesar)and zinc shot(99.99wt%,Alfa Aesar)were used as starting materials.The materials were sealed in small tantalum crucibles and vacuum quartz tubes in turn,and then heated up to 900℃ in a laboratory chamber furnace(Carbolite Gero Ltd.,UK)and kept at the temperature for 4 h followed by quenching in cold water.Both alloys were annealed at 400 and 500℃ for 30 and 10 days.The Mg75Y15Zn10alloy was further annealed at 525℃ for 15 days to checkthe phase stabilities reported in the literature[13].The alloys were ground into powder and their actual chemical compositions were measured by inductively coupled plasma(ICP),while their phase constituents were analysed using the XRD(D8-Advance,Bruker,Germany).Then,the alloys for the EPMA(JXA-8800R,JEOL,Japan)measurements were mounted,mechanically ground and polished under ethanol to reduce oxidation or corrosion.The ZAF program was used to calibrate the composition of each element at every detected point with standard samples of pure Mg,Y and Zn.

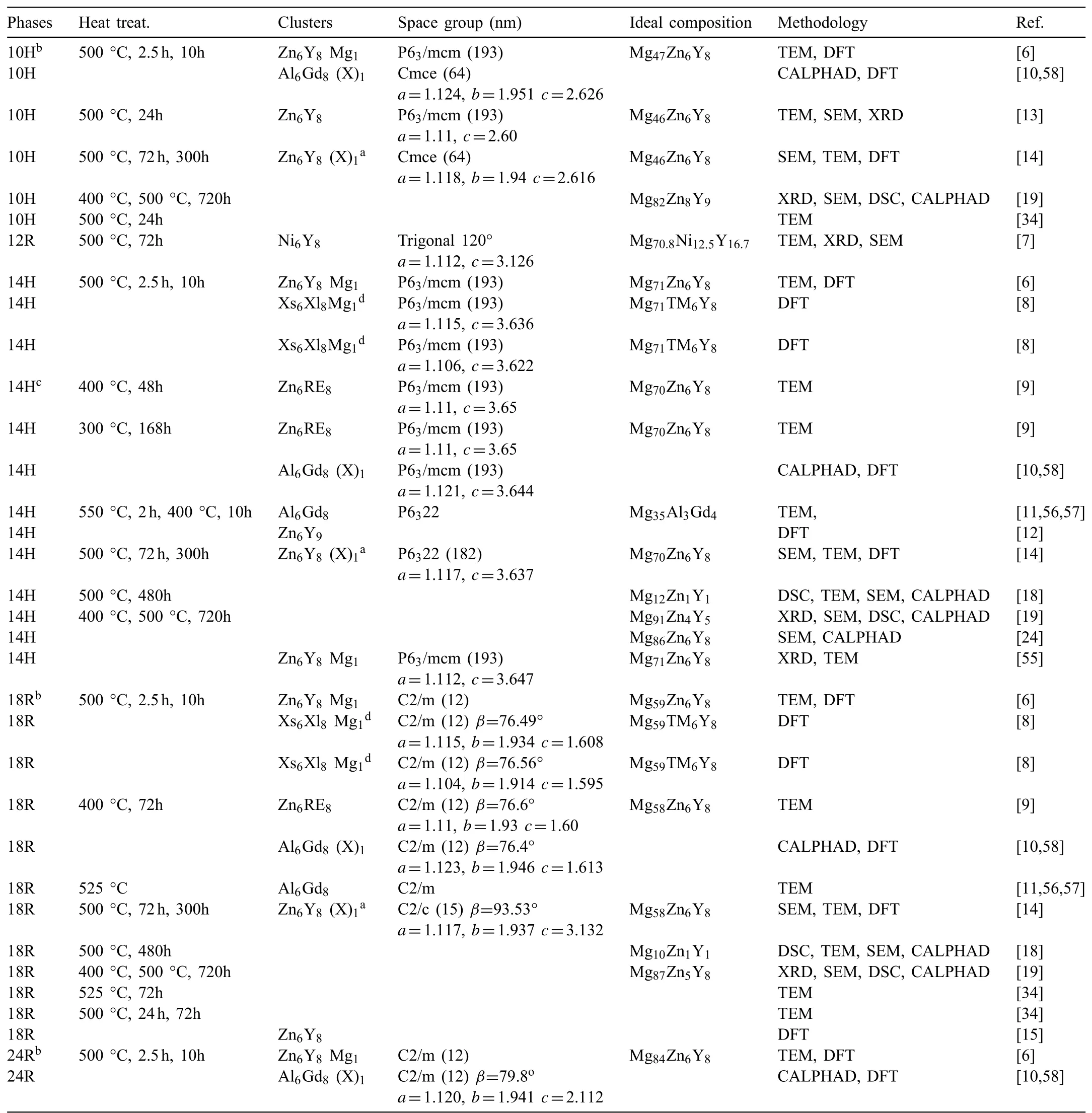
Table 1Representative structural models of LPSOs in magnesium alloys.

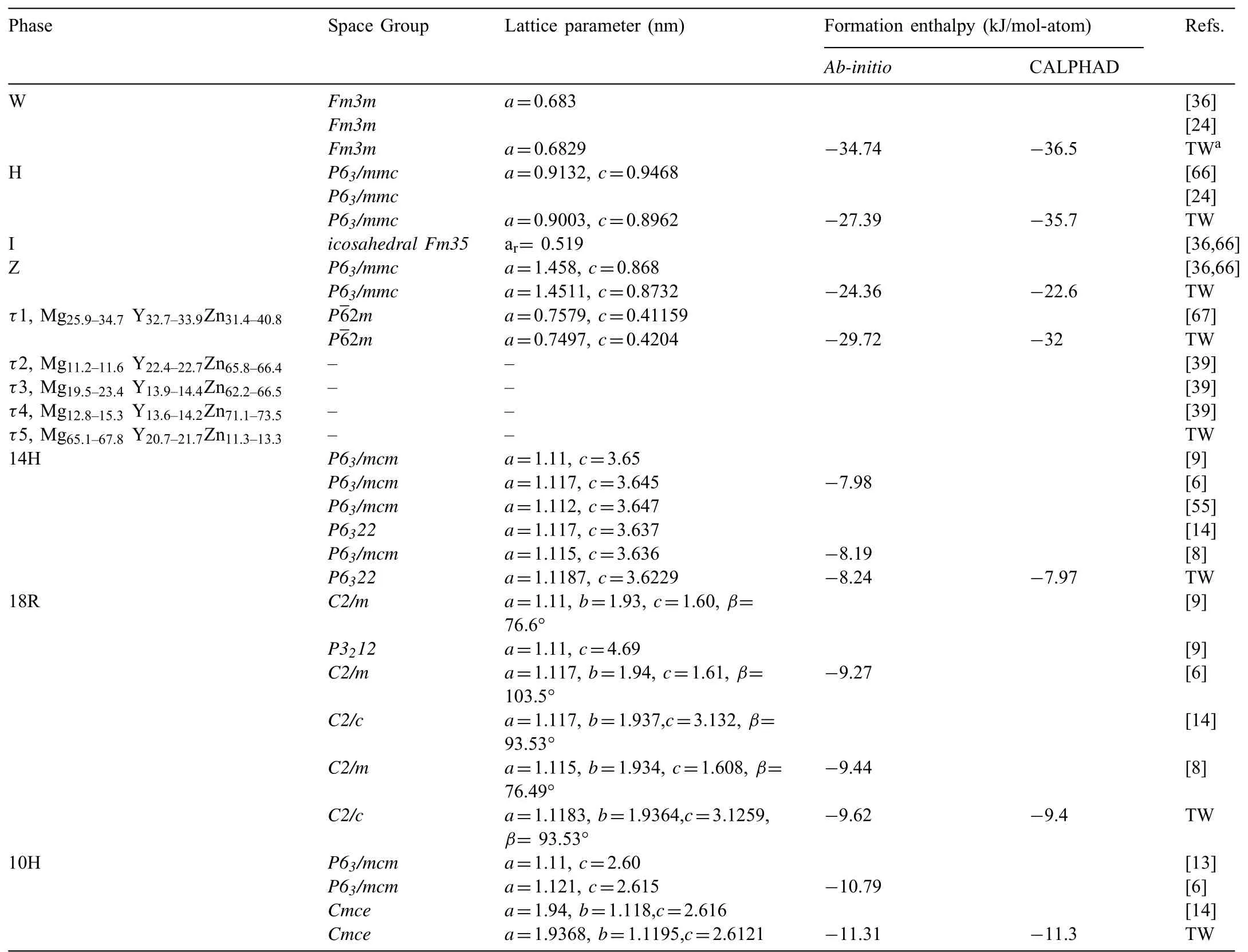
Table 2Ternary phases in the Mg–Y–Zn system.

3.Results and discussion

3.1.Thermodynamic calculations

Table 1 summarizes the representative findings on structural models for the LPSOs via transmission electron microscope(TEM),atomic-resolution scanning transmission electron microscopy(STEM),EPMA,first-principles calculations,etc.[6–15,18,19,24,34,55–57].Though the precise crystal structures of LPSOs need more detailed experimental confirmation,the existence of the Xs6Xl8(Xs and Xl are elements smaller and larger than Mg,usually,Xs=Al and some transition metals,Xl=rare earth elements)atomic clusters with the L12-type atomic arrangement in LPSOs has been widely accepted[6–15].The clusters arrange in the unit cell regularly with the Mg atoms filling in the rest positions.Kishida et al.[14]calculated the energy required to insert one additional atom i(i=Mg,Zn or Y)in the central site of each Zn6Y8atomic cluster and found a relationship of ΔEadd−Mg<ΔEadd−Y<ΔEadd−Zn<0.In addition,the experimentally determined homogeneity ranges of LPSOs always deviated from the ideal structural models[9,14,16].Considering the average atomic size of Zn and RE(Rare Earth),the simultaneous replacement of Zn and RE atoms by two Mg atoms would minimize the resultant local strains[9].Therefore,the LPSOs can tolerate a considerable degree of disorder at the Xs and Xl sites with statistical co-occupation by Mg.The degree of order and the non-stoichiometrical composition range of the LPSOs depend on the occupation of Mg at the Xs and Xl sites.For the first time,Kim et al.[10,58]applied a four-sublattice model to describe the LPSOs with different interstitial atoms in the Mg-Al-Gd system,while limited homogeneity ranges were considered during optimization.In the present work,we proposed a general thermodynamic model Mgx(Xs,Mg)6(Xl,Mg)8.With simpler lattices and fewer parameters,the crystal structure and solid solution features of the LPSOs can also be well reproduced.

Table 3Optimized thermodynamic parameters of the Mg-Y-Zn system in this worka.

Fig.1 shows the correlations between the general model(successfully applied in ternary Mg–Y–Zn and Mg–Y–Ni systems)proposed in this work and the crystal structures(Xs6Xl8-type L12clusters)[6–15]and homogeneity ranges[9,14,16]of the LPSOs.Different types of LPSOs can be distinguished by a varying number of internal Mg layers,which has 1,3 or 2 sub-layers for 10H,14H and 18R,respectively.The structural feature results in different amounts of Mg atoms.We can thermodynamically describe different LPSOs by controlling the value of x while considering the L12cluster occupied by the Mg atom in the central site[14].In detail,for the common stable LPSOs,the values of x are 47,71,35,59 or 83 for 10H,14H,12R,18R and 24R,respectively.This model can not only reflect the crystal structures of different LPSOs,but also describe their homogeneity ranges reasonably.The Gibbs energy per mole atoms of LPSO phaseis described as follows:

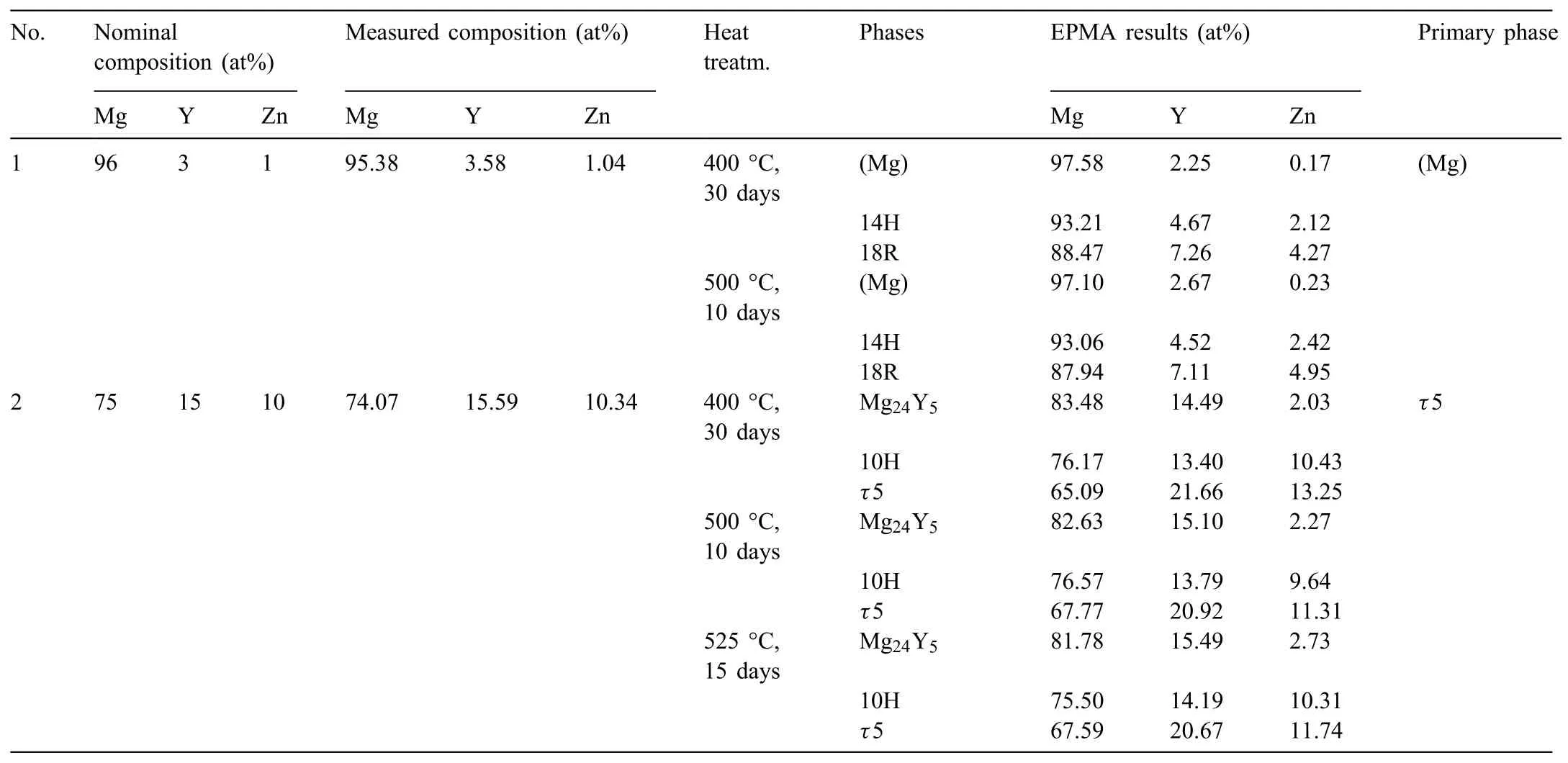
Table 4Results of XRD and EPMA in the Mg–Y–Zn system.

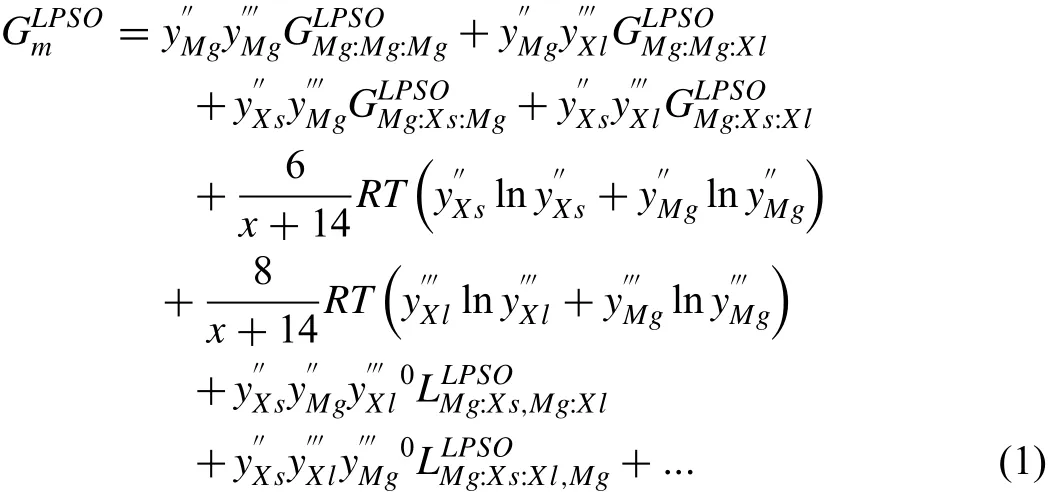
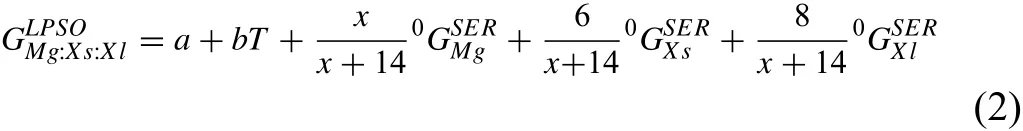
in which,a and b are the parameters to be optimized in this work.The calculated enthalpies of formation for LPSOs can be a reference equivalent for value a.

Table 2 shows the detailed crystal structure information and formation enthalpies of the stable ternary phases in the Mg–Y–Zn system.Using our model,the Mg–Y–Zn system has been optimized based on the reported experimental data[37,39],while different phase relations can be obtained due to the uncertainty of LPSOs.Three sublattices are involved in this general model,many parameters will be optimized with following strategy.There are four end-members with respect to the three-sublattice model.As presented in Eq.(2),the expressionis the Gibbs energy of the ideal stoi-LPSOs,w chiometry here the calculated formation enthalpies for LPSOs from first-principles calculations can be a reference equivalent for variable a.The other three end-members describe the solid solution ability in thermodynamics.Genmogeneity ranges carefully,while other interaction parameters are set to zero due to the little effect on the homogeneity ranges of LPSOs.

Fig.2 is the calculated isothermal sections at 400 and 500℃ using the presently obtained thermodynamic description,which was verified by our following experiments.The corresponding parameters together with the thermodynamic models are listed in Table 3.Three LPSOs(10H,14H and 18R),modeled as Mgx(Zn,Mg)6(Y,Mg)8,are stable in the Mg–Y–Zn system.Five other ternary phases(τ1-τ5)are described as stable phases for the first time,leading to the agreement between our calculations and the newly published isothermal section at 500℃[39].It should be noted that the reported phase equilibriumτ1+W+10H[39]is presently assessed and optimized to beτ1+W+18R at 500℃ based on their X-ray diffraction(XRD)and EPMA results.The threephase equilibria(Mg)+H+I and(Mg)+H+W obtained in our calculations are in reasonable agreement with the observations at 400℃[37].Moreover,two new phase equilibria(Mg)+14H+18R and Mg24Y5+10H+τ5 related to LPSOs are obtained by the present calculations at 400 and 500℃.

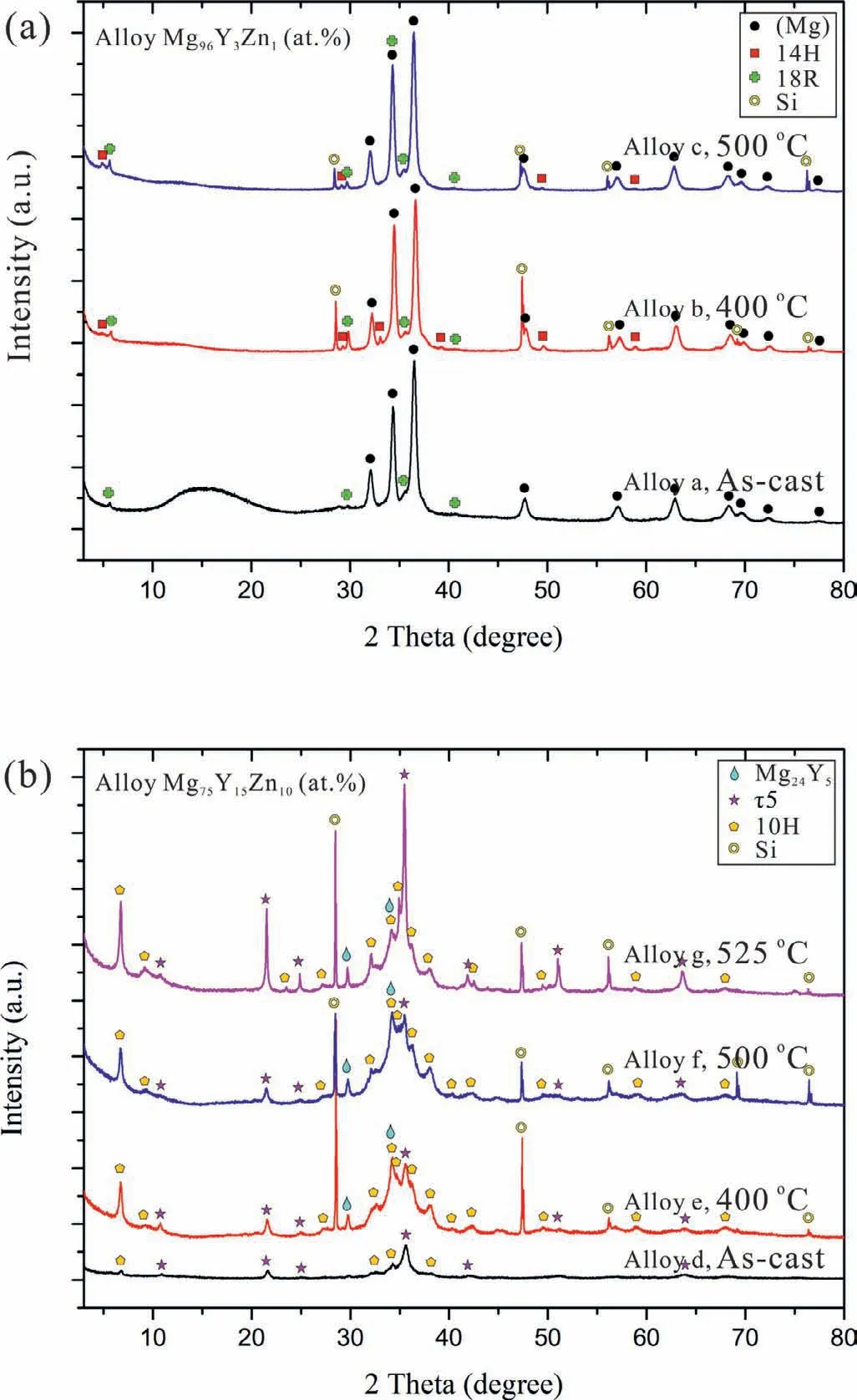
Fig.3.XRD patterns for the Mg–Y–Zn alloys at different states:(a)alloy Mg96Y3Zn1(at%),the 14H and 18R LPSOs can be indexed by the first diffraction peaks at 4.90 and 5.60℃orrespond to(002)and(001),respectively;(b)alloy Mg75Y15Zn10(at%),the 10H phase can be indexed by the first diffraction peaks at 6.90℃orrespond to(002).

3.2.Experimental confirmation

The actual chemical composition of the two alloys were measured to be Mg95.38Y3.58Zn1.04for the alloy Mg96Y3Zn1(at%)and Mg74.07Y15.59Zn10.34for the alloy Mg75Y15Zn10(at%),respectively.The determined compositions and identified phases together with the heat treatment procedures are given in Table 4.

Fig.3 shows the XRD patterns at different temperatures for comparison.From the XRD patterns of the alloy Mg96Y3Zn1(at%)shown in Fig.3a,we can identify the(Mg)phase easily.The 14H and 18R LPSO phases can be indexed by the first diffraction peaks at 4.90 and 5.60℃orrespond to(002)and(001)[8,9,14,59].However,only 18R phase can be observed in the as-cast state of this alloy.Fig.3b presents the XRD patterns of the alloy Mg75Y15Zn10(at%)at four different states.Another LPSO phase 10H,instead of 14H and 18R,is indexed by the first diffraction peak at 6.90℃orrespond to(002),as reported by Yamasaki et al.[13].Another LPSO phase 10H,instead of 14H and 18R,is indexed by the first diffraction peak at 6.90℃orrespond to(002)[13].Other peaks indicate a phaseτ5,which is rarely reported in the literature except the work of Yamasaki et al.[13].

Fig.4a–c shows the corresponding back scattered electron(BSE)images of the alloy Mg96Y3Zn1(at%).As we can see,we can first identify the(Mg)phase in this alloy,which presents as the primary phase(Fig.4a).After annealing at 400(Fig.4b)and 500℃(Fig.4c)for 30 and 10 days,the acicular 14H evolves inside the(Mg)matrix with different directions[6]and the phase relation(Mg)+14H+18R remains unchanged,which is completely distinct from the previous works[18,23].The corresponding BSE images of the alloy Mg75Y15Zn10(at%)at as-cast and annealed states are shown in Fig.4d–g.Fig.4d indicates that the bright phaseτ5 forms directly from the melts and presents as the primary phase,which is surrounded by 10H.Moreover,these phases are still stable after annealing,presenting a new three-phase equilibrium Mg24Y5+10H+τ5 at 400(Fig.4e),500(Fig.4f)and 525℃(Fig.4g)simultaneously.The experimental results give strong supports to our calculations.

3.3.Applications

Liquid phase reactions and solidification processes are of great importance to the enhancement of mechanical properties in engineering.Fig.5a is the predicted liquidus projection of the Mg–Y–Zn system together with the experiment data[37,60].Except for theτ4 phase,all the other ternary compounds(including three LPSOs:10H,14H,and 18R)have their own primary phase regions during solidification.The primary phase region of 14H does exist but is relatively limited,which is consistent with our previous observation[60].The predicted primary phase region of(Mg)is much larger than the previous calculations[18,23,24],but agrees well with the newly published experimental data[37,60].The primary phase region of I phase predicted in this work includes the alloy Mg67.5Y2.5Zn30(at%)[23],which is different from the former calculations[18,23,24].

The magnification in Mg-rich region is shown in Fig.5b,where the primary phase region of(Mg)covers the blue and green dash-dotted lines.Different Zn/Y molar ratios divided by the dash-dotted lines lead to three solidification processes according to our prediction:(i)when the ratio is lower than 0.803,there is no 14H formed during solidification;(ii)when it is higher than 0.803,14H can be precipitated after 18R with appropriate cooling rate;(iii)when the ratio is higher than 7.957,the icosahedral I phase is formed and there is no LPSO.

Fig.4.BSE images of the corresponding Mg–Y–Zn alloys in this work:(a)as-cast state for alloy Mg96Y3Zn1(at%),(Mg)presented as the primary phase;(b),(c)alloy Mg96Y3Zn1 annealed at 400 and 500℃ for 10 days,presenting a new three-phase equilibrium(Mg)+14H+18R,consistent with our calculations;(d)as-cast state for alloy Mg75Y15Zn10(at%),τ5 phase presented as the primary phase;(e)–(g)alloy Mg75Y15Zn10 annealed at 400 and 500℃ for 10 days and at 525℃ for 15 days,presenting a new three-phase equilibrium Mg24Y5+10H+τ5,consistent with the previous calculations.

Gulliver–Scheil model is one of the frequently used approximations to analyze the complicated solidification process[61–65].The solidification paths of three representative alloys Mg80Y14Zn6(wt%),Mg80Y12Zn8(wt%)and Mg90Y1Zn9(at%)located in different regions are predicted in this work.Fig.6a presents the calculated solidification path of the alloy Mg80Y14Zn6(wt%),which precipitates(Mg),18R,and Mg24Y5sequentially.The 14H phase is formed in the solidification process of the alloy Mg80Y12Zn8(wt%),as shown in Fig.6b.In Fig.6c,the I phase instead of any LPSOs is precipitated for the alloy Mg90Y1Zn9(at%).Our predictions are consistent with the reported experimental results[23,37,60].Liang[60]reported that the as-cast alloys Mg79.4Y12Zn8Zr0.6and Mg79.4Y14Zn6Zr0.6(wt%)exhibited completely different microstructures.The 14H phase was observed in the former alloy,while in the latter one,Mg24Y5was formed after the solidification of 18R.The as-cast alloy Mg90Y1Zn9(at%)was reported to consist of the(Mg)matrix and the eutectic network of(Mg)and I,no LPSOs were observed[37].

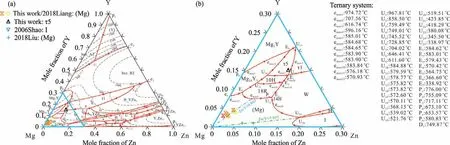
Fig.5.Predicted liquidus projection of the Mg–Y–Zn system with the applications of the general thermodynamic model for LPSOs:(a)liquidus projection and invariant reactions with experimental data[23,37,60];(b)local magnification in the Mg-rich region,blue and green dashed lines represent the divide of different solidification paths.

Fig.6.Predicted non-equilibria solidification paths of the Mg–Y–Zn alloys at different Zn/Y ratio in the Mg-rich region:(a)alloy Mg80Y14Zn6(wt%),Zn/Y<0.803[60],(b)alloy Mg80Y12Zn8(wt%),Zn/Y>0.803[60],(c)alloy Mg90Y1Zn9(at%),Zn/Y>7.957[37].

4.Conclusions

In summary,we have proposed a general thermodynamic model Mgx(Xs,Mg)6(Xl,Mg)8for the LPSOs in magnesium alloys,which can not only reflect the crystal structures of LPSOs,but also describe their homogeneity ranges reasonably.It has been successfully applied to describe the Mg-Y-Zn system.Two new three-phase regions,(Mg)+14H+18R and Mg24Y5+10H+τ5,were predicted and confirmed by key experiments.Critical conditions during non-equilibrium solidification in Mg-rich region were predicted,which is consistent with the reported data.Our general model can be extended to multi-component system.More than one Xs elements results in a general model written as Mgx(Xs1,Xs2,…,Mg)6(Xl,Mg)8,which is well confirmed by our ongoing work on the quaternary Mg–Y–Zn–Ni system(including four LPSOs:10H,12R,14H,and 18R).Moreover,if there is more detailed and reliable experimental information about the solid solution mechanisms and the interstitial atoms in the central site of the L12clusters,this model can also be further extended.

Declarations of Competing Interest

None.

Acknowledgments

This work was supported by the National Key Research and Development Plan(No.2016YFB0701202).K.Chang acknowledges the CAS Pioneer Hundred Talents Program.Professor Zi-Kui Liu is greatly acknowledged for the discussion about the general thermodynamic model for LPSOs.