基于应力约束的框架结构拓扑优化研究

何一凡 赵磊

摘 要：针对工程框架结构的强度需求，建立了应力和体积约束下框架结构柔顺度最小化的拓扑优化模型。首先，为解决应力优化过程中的应力奇异和大量局部约束问题，利用qp应力松弛技术和p范数凝聚函数法构建了应力约束的归一化等效应力约束方案。其次，提出了基于凝聚应力和变体积约束限措施的修正方案，以克服优化过程中应力约束严重非线性和最大局部应力波动等问题。再次，导出了目标函数和应力约束的灵敏度公式，并采用移动渐近线方法算法进行优化求解。最后，给出优化算例，验证了本文方法的正确性与可行性。

关键词：拓扑优化;框架结构;应力约束;应力松弛;凝聚函数法

中图分类号：TB21 文献标识码：A 文章编号：1003-5168（2021）28-00-07

Abstract： For the strength requirements of the engineering frame structures， this article establishes a topology optimization model that minimizes the flexibility of the frame structure under stress and volume constraints. In order to solve the stress singularity and deal with a large number of local constraints during the stress optimization process， a normalized equivalent stress constraint scheme for stress constraints is constructed by using the qp stress relaxation technique and the p-norm aggregation function method. Subsequently， a modified scheme based on the aggregation stress and the variable volume constraint limit measures is proposed to overcome the nonlinear problem of aggregation stress constraints and the maximum local stress fluctuation problem during an optimization process. The sensitivity formulas of the objective function and stress constraints are derived， and the MMA algorithm is adopted to optimize the model. Finally， the optimization example given verifies the correctness and feasibility of the proposed method.

Keywords： topology optimization;frame structure;stress constraint;stress relaxation;aggregate function method

拓撲优化作为结构创新设计的重要手段，已在机械、土木及航空航天等工程领域得到了广泛应用。目前，大多数研究仍关注连续体结构刚度相关的优化设计[1-4]，而强度问题是工程结构设计需要考虑的首要条件之一。因此，考虑强度的结构拓扑优化设计获得了越来越多的关注[5-8]。

近年来，涉及强度需求的连续体结构拓扑优化设计方法取得了较大进展，但由于应力约束的局部特性，优化模型中存在大量的局部约束导致优化求解困难，限制了相关研究的发展。为此，许多学者采用p范数或K-S（Kreisselmeier-Steinhauser）凝聚函数法对应力约束进行等效化处理[9]，以解决应力优化相关的大规模局部约束问题。然而，由于应力约束本身具有非线性特征，加之结构中尖端、凹槽等区域出现的应力集中现象和应力约束凝聚处理导致了应力约束的强非线性问题，使得优化结果对优化模型及优化求解器的参数高度敏感。为了规避优化结构中的应力集中现象和解决具有强非线性优化模型的求解问题，需要对凝聚参数合理取值，并修正优化模型，以自适应方式抑制设计变量大的变化。同时，应力水平的精确评估与基于梯度的优化算法的选用对克服该强非线性问题至关重要[10-11]。为此，张维声等采用两种全局应力评估方法（包括应力梯度和局部曲率信息）来控制结构的局部应力[12]。XIA等采用一种自适应的有限元技术来避免优化过程中出现的人工弱材料，以精确计算局部应力水平[13]。PICELLI等提出一种应力平均技术以提高应力求解精确性[14]，并采用自适应归一化方法以准确约束局部应力。此外，优化过程中低密度区域会引起应力奇异现象，进一步导致应力相关优化求解存在较大困难。针对该问题，许多学者提出了ε松弛和qp应力松弛技术，并成功应用到了应力相关的拓扑优化中[11]。但上述研究仍局限于连续体结构的优化设计，而工程中由梁、杆等组成的框架结构应用普遍。为推进工程框架结构的实际应用，需要进一步发展考虑应力约束的框架结构的拓扑优化方法。

考虑到工程中框架结构的强度需求，笔者提出了考虑应力及变体积限约束的框架结构柔顺度最小化的拓扑优化设计方法。为规避优化结构中的细长杆件，首先基于Heaviside映射函数构建了设计变量与物理变量的合理映射关系。其次，采用qp应力松弛技术和p范数凝聚函数对应力约束进行等效化处理，以克服应力奇异问题和大量局部约束问题。再次，基于变体积限约束方法和凝聚函数的修正方案，建立了考虑应力约束的框架结构拓扑优化的等效优化模型。最后，通过移动渐近线方法（Method of Moving Asymptotes，MMA）算法进行了优化求解，并通过两个数值优化算例说明了优化设计方法的正确性与可行性。

1 框架结构的惩罚模型和等效应力

1.1 框架结构的等效应力

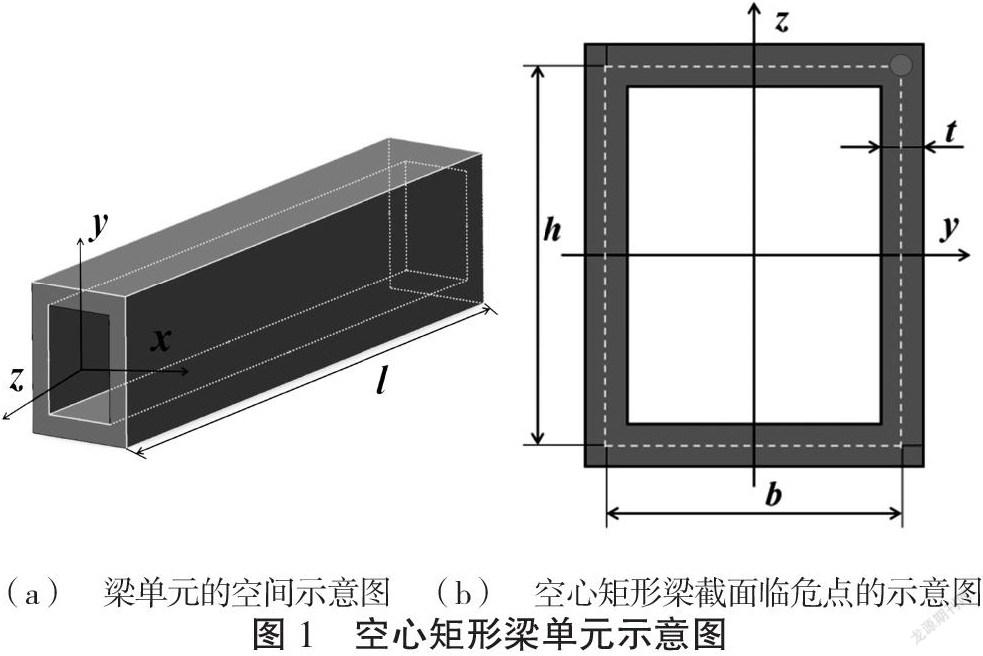
选取研究对象为由空心矩形截面的Euler-Bernoulli梁单元[如图1（a）所示]组成的框架结构。

对框架结构而言，其构件截面上应力与截面中点的位置坐标有关。将如图1（b）所示的梁单元端面黑色标注点作为该截面的临危点[15]，采用临危点应力校核结构强度设计的安全性。若b、h和t分别表示梁单元横截面的宽度、高度及厚度参数，则单元横截面积可表示为：

在如图1（a）所示的局部坐标系（x，y，z）下，梁单元的内力可表示为：

式中：Ui、Ki和Fi分别为单元整体坐标系中第i号单元节点位移矢量、在局部坐标系下第i号单元的固有刚度矩阵及其单元内力;Ti为局部坐标系与整体坐标系之间的变换矩阵，由单元局部坐标轴和结构整体坐标轴的方向余弦构成。在局部坐标系下，第i号梁单元两端截面内力可以表示为：

式中：qi1和qi2分别为第i号梁单元两端截面的内力;r11=[I6×6 06×6]，r2=[06×6 I6×6]，I6×6和06×6分别为维度为6×6的单位矩阵及零矩阵;Fx，ij表示第i号梁单元j（j=1，2）截面的轴力;Fy，ij和Fz，ij分别为相应截面平行于y和z轴的剪力;Mx，ij、My，ij和Mz，ij分别为相应截面受到的绕x轴、y轴和z轴的弯矩。

梁单元截面上任意一点的应力状态为：

其中：

式中：σF是轴向力Fx引起的正应力;σMy、σMz是弯矩My和Mz引起的弯曲应力;τMy是由扭矩Mx引起的扭转切应力;τFy、τFz是由剪力Fy和Fz引起的弯曲切应力。

第i號梁单元第j截面上临危点的Von Mises等效应力可表示为：

1.2 框架结构的惩罚模型

采用固体各向同性材料惩罚模型（Solid Isotropic Material with Penalization，SIMP）插值模型，第i号单元的刚度矩阵Ki表示为：

式中：Ki0为第i号单元局部坐标系中固有单元刚度矩阵;p为惩罚参数。为了解决结构单元灰度问题，采用Heaviside映射技术，形成设计变量与物理变量ρi映射的表达式：

式中：β为Heaviside映射曲率参数。借鉴相关文献[11]的应力奇异处理措施，可将单元体积vi、截面应力σ（jvm，t）和应力限分别表示为：

式中：vi0和表示第i号单元的固有体积和j（j=1，2）截面临危点固有应力;αv、p和q为惩罚参数;为结构固有的最大许用应力。

2 优化模型

考虑到工程框架结构的强度需求，可构建应力及体积约束的框架结构柔顺度最小化的拓扑优化模型，如式（17）所示：

式中：是拓扑设计变量向量，m为结构中梁单元的数目;为第l组载荷工况下的自适应权重系数;Ctol为组合的目标柔顺度;Cl为第l组载荷工况下的柔顺度，由式（19）给出;K为整体刚度矩阵;Ul为第l组载荷工况下整体坐标系中结构的位移矢量;Fl为第l个载荷工况;n为载荷工况数;ρi和vi0分别为第i个物理变量和第i号单元的初始体积;V（0）为初始迭代时结构的总体积;为在第l组载荷工况下第i号单元的j号截面的Von Mises等效应力值;和分别为拓扑设计变量上下限，本文取;V*为目标体积。自适应权重系数的表达式为：

式中：Cl（w）表示第w迭代步第l（l=1，2，…，n）组载荷工况下的结构柔顺度;Cl为第l组载荷工况下的结构柔顺度，其可表示为：

为了解决大量局部应力约束导致的计算量大的困难，基于qp应力松弛技术和p范数凝聚函数法，将优化模型式（17）中的大量局部应力约束近似等效为下列凝聚应力约束[15]。

式中：可以通过凝聚参数pn（pn>1）的值使得第l组载荷工况下的结构凝聚应力约束近似等效于第l组载荷工况下结构大量局部应力约束;表示第l组载荷工况下的结构第i号单元的j（j=1，2）截面临危点固有应力;为第w迭代步的值。但是，pn取值过大将使凝聚应力约束的非线性程度增大，会导致优化求解过程反复震荡;当pn取值较小时，凝聚函数无法取代包络对象的最大值。相关参考文献[16]引入系数cp，使得式（20）为紧约束，其中：

3 灵敏度分析

3.1 结构柔顺度及体积的灵敏度

由优化模型式（17）的结构柔顺度表达式可推出目标函数Ctol关于物理变量ρk的灵敏度：

式中：Ul（w）为第l组载荷工况下整体坐标系中结构第w步的位移矢量。

3.2 应力约束的灵敏度

由链式求导法则可得凝聚应力约束对物理变量的灵敏度为：

基于上述灵敏度分析，结合MMA算法，对本文所提出的优化模型进行优化求解，当满足如式（37）和式（38）所示的收敛条件时则终止迭代，得到优化解。为了进一步解决严重的非线性求解问题，在MMA迭代求解过程中采用xml对设计变量进行控制。

式中：m的初始值为1，并且其值每50个外循环迭代步增加1。

式中：和分别为第w步和第w-1步设计变量的值;md为灰度指标;ε1、ε2为两个较小的经验参数值，本文取ε1=0.01，ε2=0.01。

4 算例分析

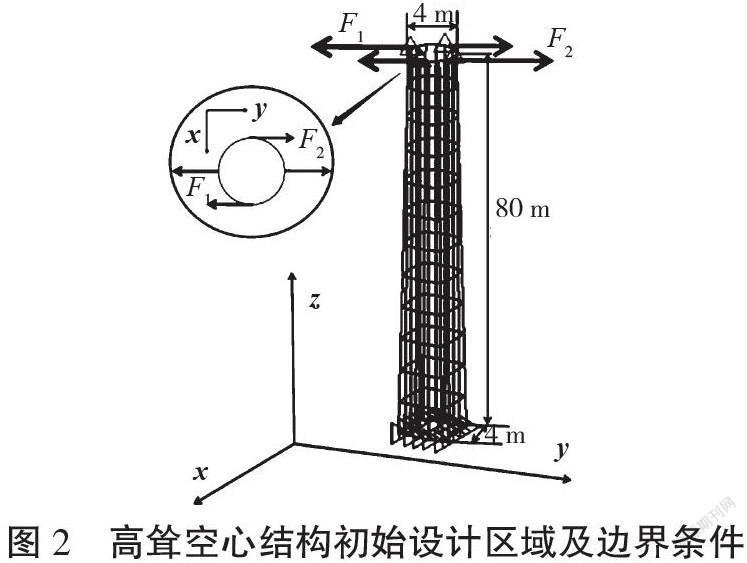
一高耸空心结构高80 m，最底部外尺寸为4 m×4 m的正方形区域，最顶部外尺寸为直径4 m的圆形区域，采用TOMÁS等[17]提出的方式生成该模型。中间空心区域是底面半径为3 m、高80 m的圆柱形区域。初始框架基结构中，梁构件的截面均为0.1 m×0.1 m且壁厚0.01 m的空心矩形截面。结构底面固定且受到如图2所示的两组方向相反的1 000 kN外载荷作用，其中F1沿y轴的反方向（工况1），F2沿y轴的正方向（工况2）。结构的弹性模量E=210 GPa，泊松比v=0.3，结构的初始最大应力为3.974 1 MPa。本算例中取SIMP惩罚参数为p=3，应力约束限的惩罚参数q=2.5，凝聚参数pn=8，目标体积为0.06，变体积限的移动步长为0.02。

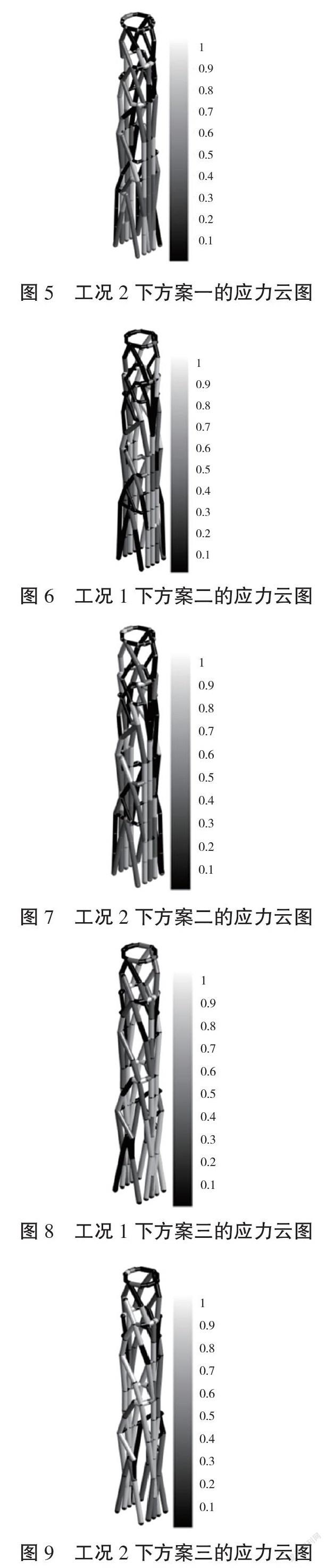
結构的初始基结构设计域如图3所示，由1 656个梁单元构成。采取4种不同的应力约束方案。方案一=3.2 MPa，方案二=3.5 MPa，方案三=5 MPa，方案四未考虑应力约束。

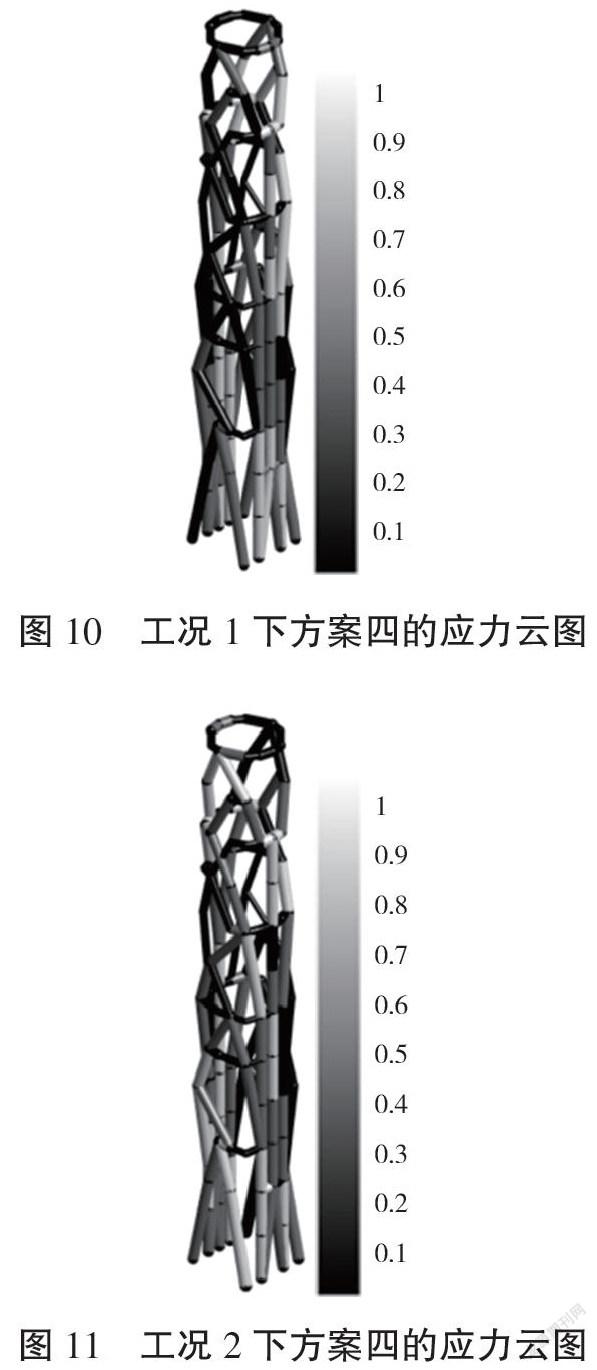
如图2所示，在工况1和工况2的共同作用下，结构在不同应力约束限下的优化拓扑及其应力云图分别如图4至图11所示。可知，框架结构的优化拓扑随应力约束限的不同产生细微变化，而相应的应力云图随应力约束限的不同产生较大变化。由图4至图11的对比分析还可以看出：有无考虑应力约束的优化结果存在明显不同。

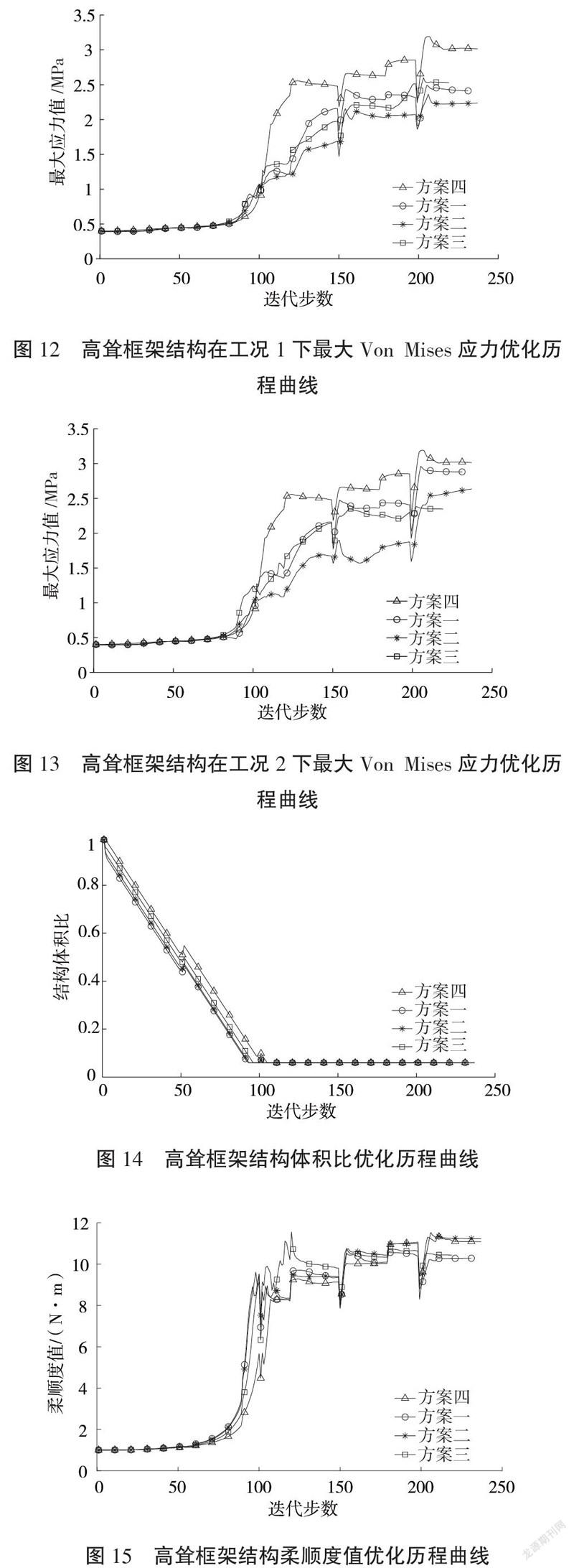
结构在不同约束限下的柔顺度、最大Von Mises应力及结构体积的迭代历程曲线分别如图12至图15所示，可知：优化过程稳定收敛，且其优化结构的柔顺度和最大应力都随杆件减少而增大。对应图4至图9中优化构型的最大应力分别为2.880 9 MPa、2.6345 MPa及2.529 7 MPa，其最终柔顺度分别为10.284 6 N·m、11.231 6 N·m和10.435 1 N·m。图10和图11中未考虑应力约束的优化构型的最大应力为3.014 2 MPa，其最终柔顺度为11.088 7 N·m。由此可知，优化结构的最大应力也随不同应力约束限而不同，且优化结构的最大应力随应力约束限的增大而增大，而其柔顺度未发生明显变化。同时，考虑应力约束的优化结构的最大应力明显小于未考虑应力约束的优化结果。可见，提出的方法有效控制了优化结构的最大应力，得到的拓扑优化结果是满足应力约束且合理的。

5 结论

针对框架结构的强度需求，基于SIMP插值模型和Heaviside映射函数建立了应力及体积约束下框架结构轻量化拓扑优化模型。采用qp应力松弛技术和p范数凝聚函数法构建了等效应力约束函数，通过凝聚应力约束修正方案和变体积约束限方法形成了相应的等效优化模型。此外，进一步解决了严重的非线性模型求解问题，对每一步设计变量的变化范围进行了控制。最后，通过数值算例来说明所提出优化方法的正确性与可行性，并得到如下结论。

①本方法能获得稳定收敛的解，且能得到满足应力约束的清晰优化拓扑。

②结构的优化构型随应力约束限的不同而发生变化，且其柔顺度和最大应力都随杆件的消除而增大。

③考虑应力约束的优化结构的最大应力明显低于未考虑应力约束的最大应力。提出的方法有效控制了优化结构的最大应力，得到的拓扑优化结果满足应力约束且合理。

参考文献：

[1]DUYSINX P， BENDSOE M P. Topology optimization of continuum structures with stress constraints[J]. International Journal for Numerical Methods in Engineering， 1998（8）：1453-1478.

[2]ZHU J H， GUO W J ， ZHANG W H， et al. Integrated layout and topology optimization design of multi-frame and multi-component fuselage structure systems[J]. Structural and Multidisciplinary Optimization， 2017（1）：21-45.

[3]冷国俊， 张卓， 保宏， 等.考虑重叠过滤及稳定性约束的桁架拓扑优化方法[J].工程力学， 2013（2）：8-13.

[4]CUI H， AN H， HUANG H . Truss topology optimization considering local buckling constraints and restrictions on intersection and overlap of bar members[J]. Structural and Multidisciplinary Optimization， 2018（2）：575-594.

[5]CHANGIZI N， KABOO DA NIAN H， JALALPOUR M. Stress-based topology optimization of frame structures under geometric uncertainty[J]. Computer Methods in Applied Mechanics and Engineering， 2017， 315：121-140.

[6]JEONG S H， CHOI D H， YOON G H . Separable stress interpolation scheme for stress-based topology optimization with multiple homogenous materials[J]. Finite Elements in Analysis & Design， 2014（5）：16-31.

[7]GAO X J， LI YX， MA H T， et al. Improving the overall performance of continuum structures： a topology optimization model considering stiffness， strength and stability[J]. Computer Methods in Applied Mechanics and Engineering， 2020，359：112660.

[8]LE C， NORATO J， BRUNS T， et al. Stress-based topology optimization for continua[J]. Structural and Multidisciplinary Optimization， 2010（4）：605-620.

[9]王選， 刘宏亮， 龙凯， 等.基于改进的双向渐进结构优化法的应力约束拓扑优化[J].力学学报， 2018（2）：385-394.

[10]PARÍS J， NAVARRINA F， COLOMINAS I， et al. Topology optimization of continuum structures with local and global stress constraints[J]. Chinese Journal of Theoretical & Applied Mechanics， 2009（4）：98-104.

[11]MOON S， YOON G. A newly developed qp-relaxation method for element connectivity parameterization to achieve stress-based topology optimization for geometrically nonlinear structures [J]. Computer Methods in Applied Mechanics and Engineering， 2013（3）：226-241.

[12]ZHANG W， GUO X， WANG M， et al. Optimal topology design of continuum structures with stress concentration alleviation via level set method [J]. International Journal for Numerical Methods in Engineering， 2013（9）：942-959.

[13]XIA Q， SHI T， LIU S， et al. A level set solution to the stress-based structural shape and topology optimization [J]. Computers & Structures， 2012（1）：55-64.

[14]PICELLI R， TOWNSEND S， BRAMPTON C， et al. Stress-based shape and topology optimization with the level set method [J]. Computer Methods in Applied Mechanics and Engineering， 2018（1）：1-23.

[15]ZUO W， YU J， SAITOU K. Stress sensitivity analysis and optimization of automobile body frame consisting of rectangular tubes[J]. International Journal of Automotive Technology， 2016（5）：843-851.

[16]龙凯， 王选， 吉亮.面向应力约束的独立连续映射方法[J].力学学报， 2019（2）：320-329.

[17]TOMÁS ZEGARD， PAULINO G H . GRAND3— Ground structure based topology optimization for arbitrary 3D domains using MATLAB[J]. Structural & Multidisciplinary Optimization， 2015（6）：1161-1184.

3424500338229