电子地图轨道地理坐标描述方法研究

陈志强，鲍鹏宇

(1.北京全路通信信号研究设计院集团有限公司，北京 100070；2.北京市高速铁路运行控制系统工程技术研究中心，北京 100070)

列控系统车载设备测速测距传感器无法消除距离的累积误差，需要在地面铺设大量应答器设备进行位置校准，这增加了地面设备维护工作量[1-3]。由于卫星定位系统进行列车定位时无累计误差，可替代应答器设备实现列车位置校准[4-6]。2020 年6 月23 日北斗三号最后一个组网卫星发射成功，北斗三号全球卫星导航系统星座部署已全面完成，这给卫星定位系统在铁路列车控制领域的应用打下了基础和机遇。然而由于卫星定位提供的是经纬度二维坐标，而列控系统使用的是一维的轨道相对位置，为将二维的卫星坐标映射到一维的轨道上，需要提供轨道的坐标电子地图数据。本文基于此问题，对轨道电子地图的生成方法展开研讨。

1 轨道近似描述方法

铁路轨道可使用直轨和弯轨进行近似描述[7-8]，其中直轨可用直线段上的点进行描述，而弯轨包含两种描述方法：曲线描述法和线段近似法。

1）曲率描述法

曲率描述法即直接使用包含曲率半径R 和角度α 的曲线描述一段弯轨，如图1（a）所示。

2）线段近似法

线段近似法即在弯轨上选择若干个近似点，连接近似点形成若干个近似线段，使用若干个线段近似描述一段弯轨，如图1（b）所示。

比较曲率描述和线段近似两种方法：

1）参数比较：曲率描述法使用R 和α 两个参数即可描述一段弯轨，运算参数较少。而线段近似法需要包含若干个分段点的经纬度坐标，参数较多；

2）算法复杂度比较：二维卫星定位点向一维轨道投影时，曲率描述法需要大量使用三角函数运算，算法复杂。线段近似法直接进行线性运算，算法简单；

3） 工程难度比较：曲率描述法的R 和α 工程测量困难，而线段近似法的分段点工程测量简单。

图1 轨道描述方法Fig.1 Track description method

综上所述，线段近似法虽然数据量稍大，但算法简单和工程测量难度小，具有更好的可行性。

2 线段近似方法

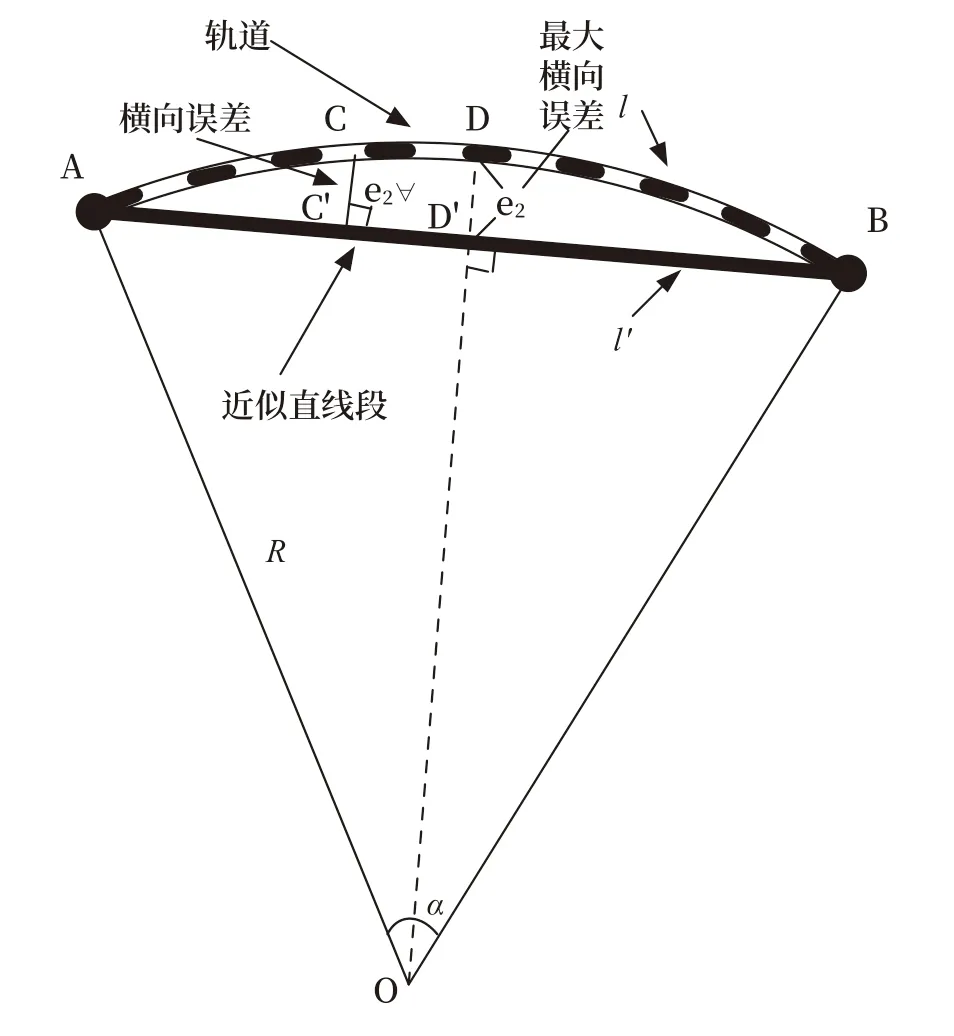
图2 线段近似算法Fig.2 Line segment approximation algorithms

1） 纵向误差和最大纵向误差

其中，

将公式（2）和（3）代入公式（1）有

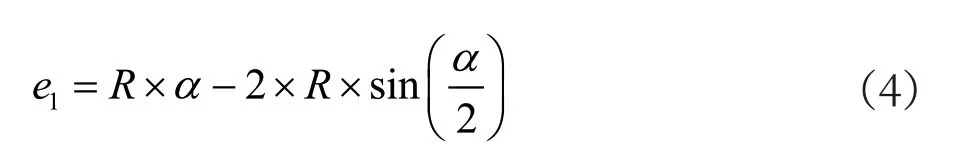
将公式（4）进行化简，有

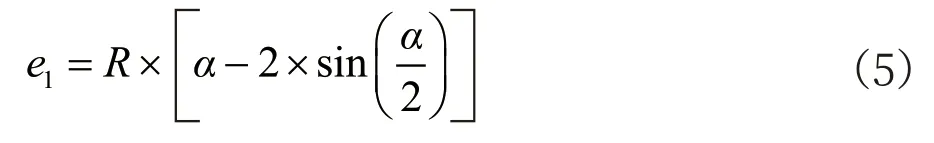
2）最大横向误差

点C 的横向误差为CC′。

其中，

将公式（7）和（8）代入公式（6）有

将公式（9）进行化简，有

由公式（2）可知

将公式（11）分别代入公式（5）和（10），可以得到误差和运行距离l 及曲率半径R 的关系

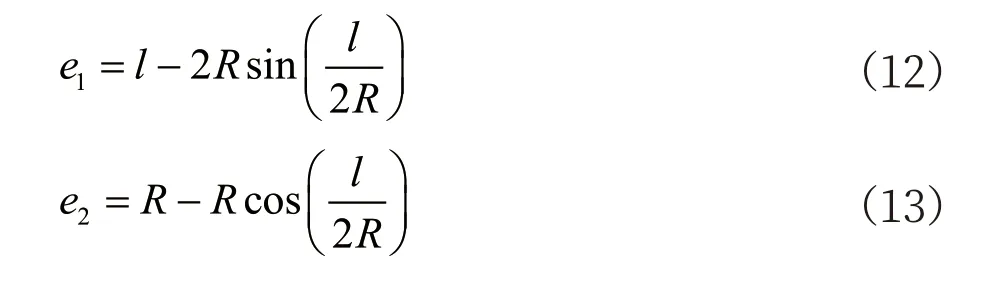
3 误差控制方法

由于实地测量的轨道卫星坐标误差需控制在固定范围（设为emax）内。由公式（12）和（13）可知，当曲率半径固定时，误差只与运行距离l 相关，对公式（12）和（13）中的l 求导，可得到

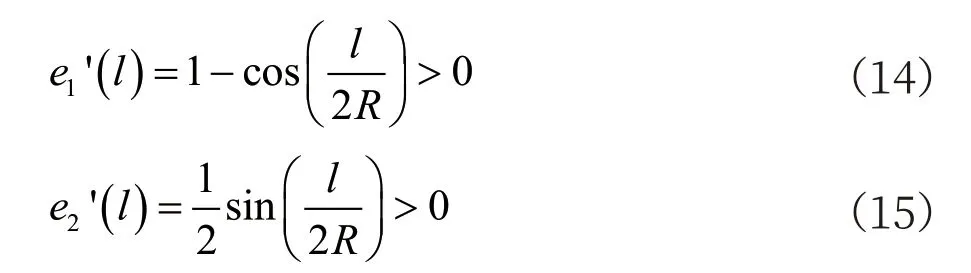
由公式（14）和（15）可知，当曲率半径固定时，随着l 的增大，误差e1和e2逐渐增大。因此使用线段AB 近似圆弧时，若误差超过emax，可通过在AB 间增加若干个近似点的方法缩短距离l，进而减小误差。

定理1：当运行弧长l ∈[0,2Rarctan(0.5)]时，横向误差大于等于纵向误差。

证明：

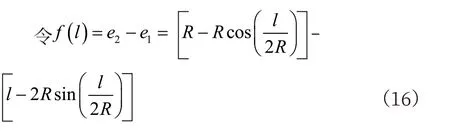
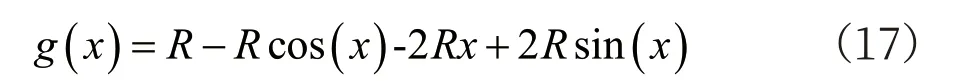
x=0 时有g(0)=0，将g(x)对x 求导，有

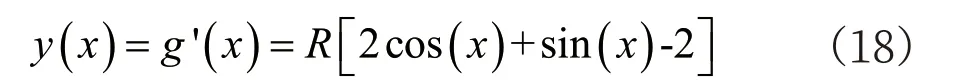
x=0 时有y(0)=0，将y(x)对x 求导，有

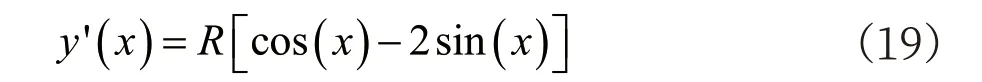
易知，当x ∈[0,arctan(0.5)]时，有y′(x)≥0，即y(x)在[0,arctan(0.5)]内是增函数。由于y(0)=0，有x ∈[0,arctan(0.5)]时，y(x)≥0。

同理，有x ∈[0,arctan(0.5)]时，g(x)≥0，即e2≥e1。

由于l=2Rx，有l ∈[0,2Rarctan(0.5)]时，e2≥e1。

证毕。

根据定理1 可知，当l ＜2Rarctan(0.5)时，横向误差大于纵向误差，因此在此范围内可使用公式（20）计算最大误差e 时的弧长l 值。

可将工程允许的最大误差带入公式（20）中，即可获得最大圆弧长度用以限定近似点间隔。

4 仿真计算

根据应用公式（13）和定理1，可得到各曲率半径下弧线长度l 和最大误差之间的关系，以及弧线长度l 满足定理1 的最大值lmax，如表1 所示。

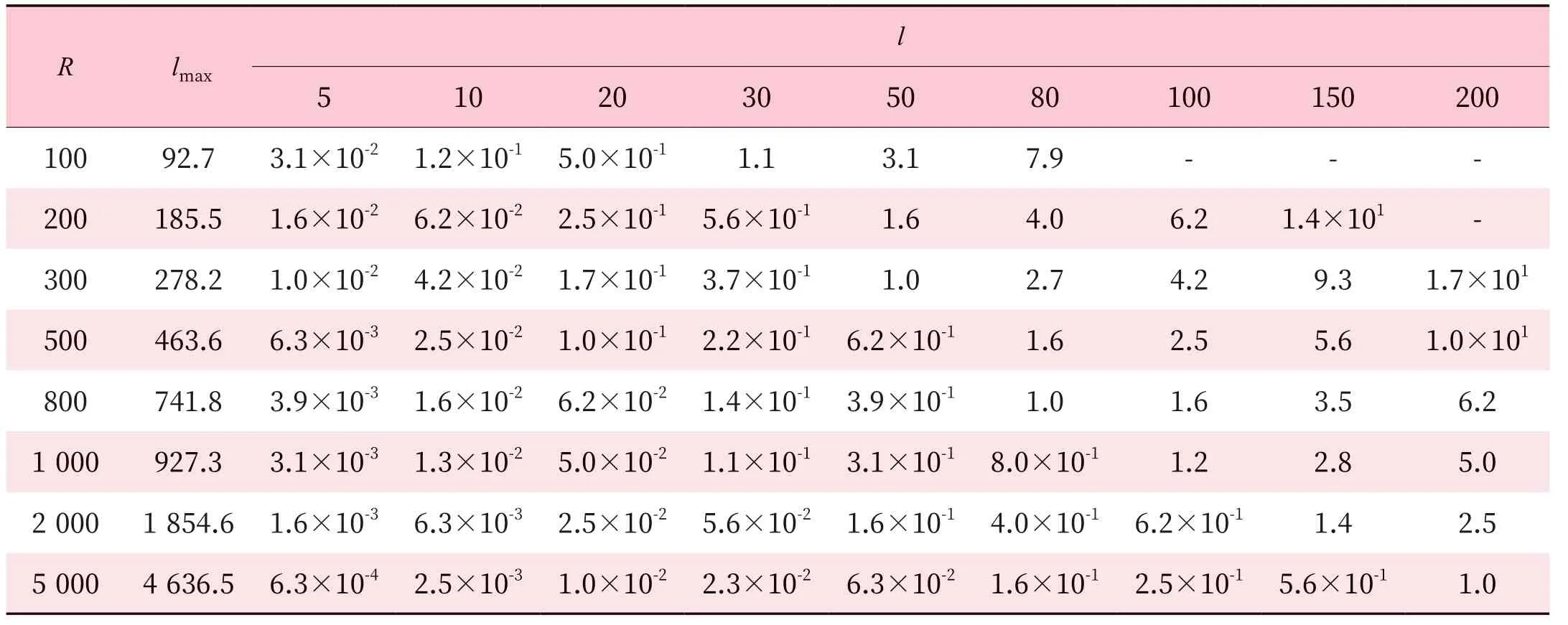
表1 弧线长度和最大误差的关系Tab.1 Relationship between arc length and maximum error m

根据表1 可生成弧长误差关系曲线，如图3 所示。如表1 和图3 所示，若曲率半径不小于300 m，则轨道的采样间隔弧长最小为50 m 即可满足1 m的精度要求；轨道采样间隔弧长最小为20 m 即可满足0.2 m 的精度要求。且随着曲率半径的增加或最小误差的增加，采样间隔弧长逐渐增加。

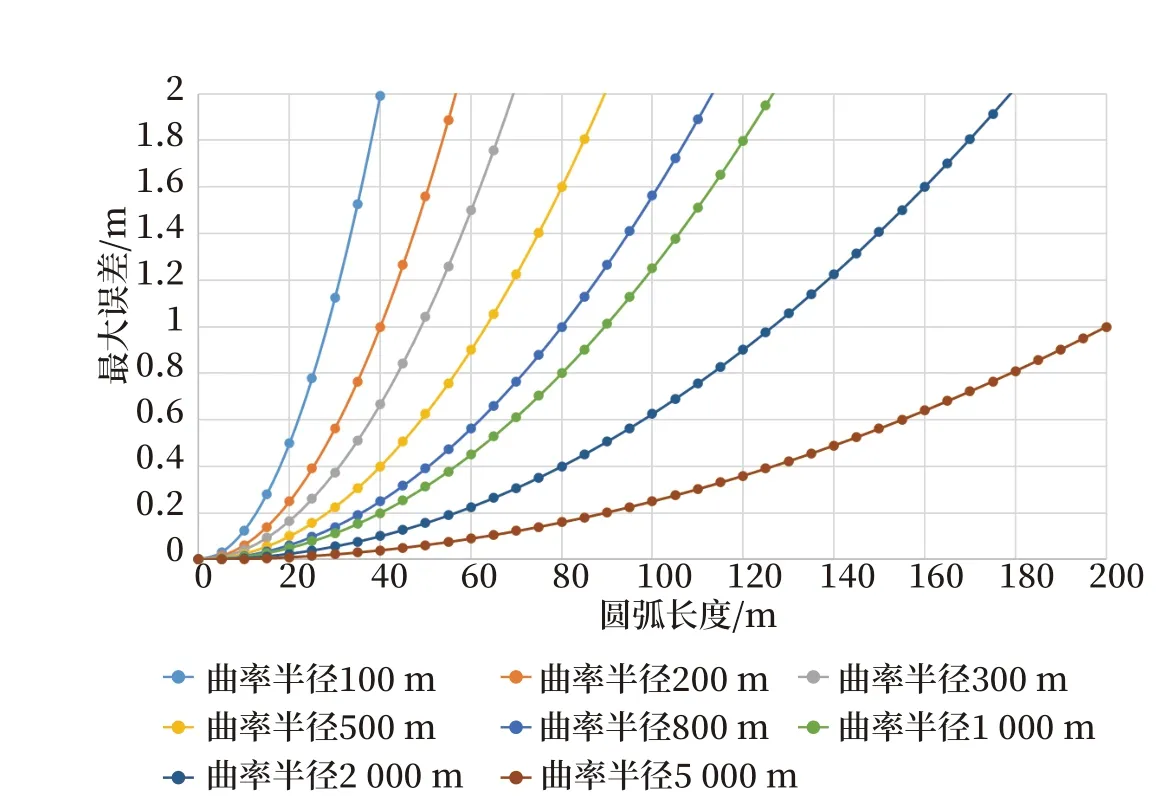
图3 弧线长度和最大误差的关系曲线Fig.3 Relation curve between arc length and maximum error

5 结论

本论文首先对电子地图中弯轨的曲线描述法和线段近似法两种方法的优缺点进行分析，得出线段近似法更易于应用和实施的结论，然后对线段近似法的误差进行分析，提出线段近似法中近似点间隔的确定方法。该方法既可以满足地图描述精度要求，又能最大程度上降低电子地图的数据量。本论文提出的电子地图描述方法，为卫星定位系统在列控系统中的有效应用提供了切实可行的方法和理论支撑。