山地风电场微观选址造成风电机组发电量偏低问题分析及移位改造方法研究

摘 要：受部分山区地形复雜的影响，风电场微观选址工作面临很多困难。为解决复杂地形风电场微观选址过程中个别风电机组的实际发电能力严重低于设计值等问题，基于CFD数值模拟，提出利用冗余机位对发电量偏低的风电机组进行移位改造的选址测算方法。选取黑龙江省某山地风电场改造后的实际发电效率进行比对验证，结果表明，该方法简单有效，能够准确模拟测算风电场及其周围可再生资源情况，对复杂山区地形下风电场的微观选址具有理论参考价值。

关键词：风电场;微观选址;复杂地形;发电效率

0    引言

随着世界范围内可再生能源的迅速发展，风能作为最具发展前景的清洁能源之一受到广泛关注[1]。风力发电技术以其独有的优点发展迅速，我国风电机组的装机容量也呈指数型的爆炸式增长模式，截至2019年底，我国并网风电装机容量达21 005万kW[2]。随着风电场规模的不断增大，风电场的微观选址、移位改造和机组的合理布局对提高风电场的发电效率、合理利用风能资源、正确预测机组发电能力等具有重要意义[3]，在一定程度上也可提高风电场的并网能力，保证电力经济的可持续发展[3]。

考虑到风电场选址一般为复杂的山地，需计及高低起伏变化的地面效应对发电效率产生的影响[4]，同时复杂地形上的风电场较戈壁滩单一地形相比，其脊谷交错、地势起伏，局部的山谷对发电效率的影响比较显著[5]。国内外众多学者对复杂地形的风电场微观选址问题进行了相关的研究[6-9]，如利用再分析数据法，模拟风向对风机布置的影响[10];较为细致地对机位优化、尾流问题进行了理论研究[11]等。但上述研究仅停留在理论研究与模拟阶段，通过实地勘验，在现实中复杂地形风电场微观选址的过程中还存在许多问题，如测风塔、等高线等其他限制因素[4]。

随着计算机技术的不断发展，CFD数值模拟方法[12]能够较好地再现流体环绕复杂几何的流动状况，这种新型的方法被越来越多地应用于复杂地形的风电场微观选址问题的研究上。文献[13]表明CFD数值模拟方法能够对复杂地形甚至极端陡峭地形下的风场的流体状况进行模拟;文献[14]采用CFD模拟再现实际地形中的风电场，分析网格、湍流模型的不同对风旋涡位置与速度分布的影响;文献[15]利用CFD分析软件模拟峡谷地形中的风流动规律。目前利用CFD数值模拟分析风电场的微观选址问题的研究仍处于起步阶段，对山坡、山丘、脊谷等方面还需要进一步的研究。

本文基于CFD数值模拟，提出利用冗余机位对发电量偏低的风电机组进行移位改造的选址测算方法。选取黑龙江省某山地风电场改造后的实际发电效率进行比对验证，结果表明，该方法简单有效，能够准确模拟测算风电场及其周围可再生资源的情况，对复杂山区地形下风电场的微观选址具有理论参考价值。

1    CFD数值模拟法

1.1    流动控制方程

基于雷诺时均的质量与动量守恒方程如下：

式中：ρ为流体密度;t为时间;xi、xj分别为i、j方向上的坐标;μi、μj分别为流体速度沿i、j方向上的分量;p为静压力;τij为应力矢量;gi为i方向上的重力分量;Fi为由压力和能源而引起的其他能源项。

1.2   湍流模型

利用网格（Gigid）对风力机进行数值计算，选择RNC k-ε湍流模型，该模型能够适用于旋转流场的分析与建模。RNC k-ε湍流模型如下：

式中：k为湍流动能;ε为湍流动能耗散率;Gk为由层流速度梯度而产生的湍流动能;Gb为由浮力而产生的湍流动能;YM为在可压缩湍流中过度扩散产生的波动;αk、αε分别为k方程和ε方程的普朗特常数;C1ε、C2ε、C3ε为常数;Sk、Sε为修正系数。

与标准k-ε湍流模型不同，RNC k-ε湍流模型增加了考虑低雷诺数流动粘性的解析式，在添加约束条件的同时，考虑湍流旋涡，并将标准k-ε湍流模型中的变量变为湍流普朗特常数提供的解析式，有效提高了计算精度，使得RNC k-ε湍流模型更加适用于旋转流场分析。

2    实例分析

2.1    算例概况

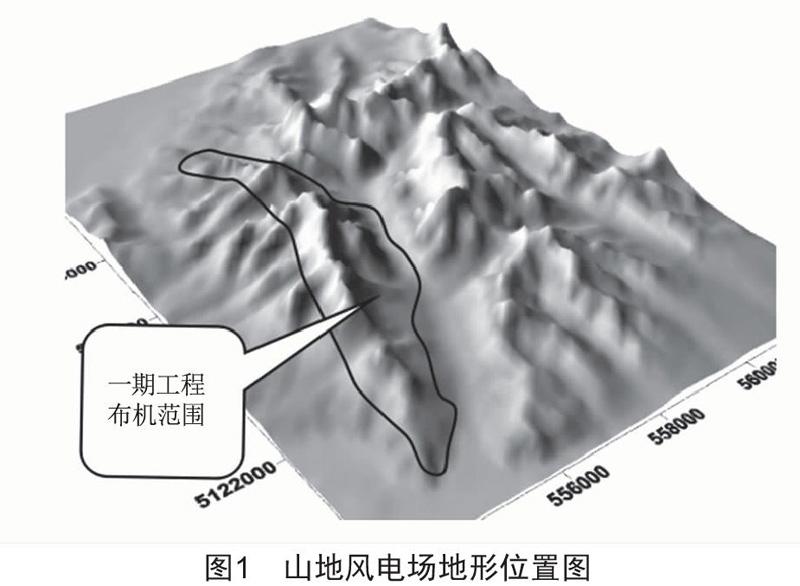
黑龙江省某山地风电场如图1所示，地形起伏较大，地面高程为170～357 m的低山丘陵。风电场一期工程于2004年6月开展测风工作，2007年核准开工建设，装机容量49.5 MW，安装33台FD-70B/1500型风力发电机组，2008年首台机组发电，2009年9月全部机组并网发电。自投运以来，#20风电机组的年发电量只有212万kWh，仅为微观选址的理论发电量的65.9%，相当于风电场单机年平均发电量的66%左右，严重偏离设计值，且故障率相对较高（处于山坡边缘，风速不稳定，湍流强度大）。为提升该风电机组的发电能力，改善其运行环境，于2012年对其进行了移位改造。

根据风电场微观选址报告，风电场主导风向为西风，风电场微观选址布机情况如图2所示。由图可见，#20风机处于主风向山脉东侧，且海拔高度低于西侧山脉70多m，前后两排最近距离只有600 m，造成该位置风速明显小于设计风速，且风电机中心位置距山坡边缘约30 m，山谷深度约85 m，坡度约65°。实际运行后风速极不稳定，导致该机组故障较多。

#20机组年实际运行对比情况如表1所示。

由表中数据可见，无论风速还是发电量，#20风电机组都与风电场平均值偏差较大。该风电机组年可利用率93.20%，低于全风电场年可利用率97.80%的水平。考虑剔除该风电机组可利用率不同的影响，这里将该机组的年可利用率按风电场平均值进行修正，修正后的年发电量2 240 MWh，与风电场平均发电量的相对值为70.20%。主要原因是微观选址等方面存在问题，具体如下：

（1）当时的微观选址软件处理复杂地形能力不足。當时采用的微观选址软件为WASP，软件地形模型算法简单，没有CFD功能，处理山地风电场湍流问题存在一定困难，特别是应对一些复杂地形更显不足。

（2）地形图数据精度不高。当时用的是1：10 000的数字地形图，由于精度不高，不能充分反映现场地形的复杂状况。

（3）设计选址人员经验不足。选址人员没有充分考虑#20机位处于地势变化较大的山谷边缘，造成该机位湍流强度大，风速不稳定，同时也没有避开主风向前方山峰的遮挡。

（4）测风数据代表性不强。测风塔的位置不在风电场区域内，测风塔的高度只有50 m，小于轮毂高度65 m，测风塔的位置海拔较低。

2.2    方案设计

依据风电场微观选址报告，当时初步选择时有44个机位，首先从中选定了3个备选机位，位置情况如图3所示。3个备选机位的微观选址情况如表2所示，3个备选机位中，备选一，平台狭小，离附近机位距离近，地势陡峭，且处于主风向下方;备选二，离周围风机距离较近，它的尾流对其后方3台机组的影响较大;备选三，地势平坦，平台面积大，地形与附近机组相似，且只会对其后面1台机组造成尾流影响。

利用风电场近两年实际运行数据，对选定的3个备选机位，利用其临近机组年发电量数据进行了比对分析，如表3所示。

通过计算结果比对，并根据现场地形情况，最终确认将#20风电机组移位至#33风机附近的备选三号机位。安装于新机位的#20风电机组年发电量约290万kWh，风电机移位后比原机位每年多发电78万kWh，发电能力提升了36.8%。各机组发电量通过下式计算：

式中：W为新机位年理论发电量;k为修正系数（考虑机组性能差异、风资源水平年差异因素影响修正值，建议取值0.9～1.0，本例中选取0.95）;Ws为备选机位临近机组年实际发电量;Wb为微观选址年发电量;Wl为备选机位临近机组年理论设计发电量。

由于当初项目已经多征用了11个机位的土地，集电线路设计也存在冗余，3个备选机位在道路、风机及箱变基础、机组拆除和安装、集电线路等方面施工条件相近，施工费用近似相同，所以在点位选择时仅考虑发电量最优方案即可。

2.3    实施过程

对#20风电机组进行了移位改造。主要工作包括：新建一段道路、一个风电机组和机组变压器基础，风电机组的拆除和重新安装，电缆、光缆的敷设。工期2个月，改造费用合计136万元。

2.4    改造效果

项目实施后效果明显。对改造后6年的数据进行分析，年平均风速6.72 m/s，年平均发电量288万kWh，年增加发电量76万kWh，年增加收入46万元，累计增收278万元。

该机位风速稳定，每年可利用率都在95%以上，平均年可利用率97.4%，风电机故障停机次数减少60%。移位后，原#20机位附近的#19风电机组发电量也得到了一定提升。

3    结语

这次移位改造的实际运行情况和改造方案的理论计算十分接近，主要原因如下：一是熟悉现场的风资源及地形状况，掌握了第一手资料;二是本文比对计算法虽然简单，却消除了风资源、地形等因素的影响，将不同位置风机发电量与风速的非线性关系转化为发电量与临近风机发电量的线性关系。由于微观选址工作至关重要，直接关系到风电项目收益，必须高度重视，尤其是复杂地形的情形。要选用合适的选址工具软件，具备CFD功能，能够很好地处理复杂地形;要有高精度的地形图（地势平坦1：5 000，地形陡峭复杂1：2 000）;具有代表性的测风数据，测风塔一定在开发区域内，且位置具有代表性，测风塔的高度大于轮毂高度，测风塔的数量要足够;由经验丰富的人员开展微观选址工作。一旦出现因微观选址问题导致发电量偏低的机组，要尽早采取有效措施对其进行移位改造。制定移位改造方案时，应结合风电场实际情况，利用现有风电机组实际的风速和发电量数据，采用有效方法，提高移位改造的经济性。

[参考文献]

[1] 刘振亚.构建全球能源互联网 推动能源清洁绿色发展[J].华北电业，2015（6）：4-7.

[2] 王恰.中国风电产业40年发展成就与展望[J].中国能源，2020，42（9）：28-32.

[3] SONG M X，CHEN K，WANG J.A Two-level Approach for Three-dimensional Micro-siting Optimization of Large-scale Wind Farms[J/OL].Energy，2020，190.[2020-12-13].https：//doi.org/10.1016/j.energy.2019.116340.

[4] 王红光，赵海军，段晓辉.复杂地形风电场微观选址实践探讨[J].南方能源建设，2019，6（2）：59-63.

[5] 左薇，李惠民，芮晓明，等.风电场山坡地形的数值模拟研究[J].太阳能学报，2019，40（5）：1441-1447.

[6] 王洁，许昌，韩星星，等.基于风力机尾流排斥的平坦地形风电场微观选址优化[J].电力系统自动化，2020，44（15）：62-69.

[7] 李俊凯，葛莹，鲍倩，等.利用地理场景的风电场微观智能选址方法[J].测绘科学，2020，45（4）：199-206.

[8] 李岩，吴迪，刘怀西，等.海上风电场微观选址及输电线路规划研究[J].风能，2019（10）：58-63.

[9] 张文静.风电场选址探究[J].湖北农机化，2019（13）：83.

[10] 蔡彦枫，王海龙，周川，等.风向对广东海上风电场风机布置的影响[J].南方能源建设，2016，3（4）：113-118.

[11] 许昌，杨建川，李辰奇，等.复杂地形风电场微观选址优化[J].中国电机工程学报，2013，33（31）：58-64.

[12] 牟林，董书宁，郑士田，等.基于CFD-DEM耦合模型的阻水墙建造过程数值模拟[J].岩土工程学报：1-11（2020-

10-27）[2020-12-13].https：//kns.cnki.net/kcms/

detail/detail.aspx？dbcode=CAPJ&dbname=CAPJLAST&-

filename=YTGC20201026004&v=ry1MXR9JKJajihGeUOG3-

WTkTKfl7G3-dg63FNqLzwuOCcuUqWUeGqQsU0c3k9OOCk.

[13] 杨昆，姜婷婷，朱金奎，等.大规模风电场实际尾流分析与算法研究[C]//第七届中国风电后市场交流合作大会论文集，2020：81-86.

[14] 李磊，张立杰，张宁，等.FLUENT在复杂地形风场精细模拟中的应用研究[J].高原气象，2010，29（3）：621-628.

[15] 霍相五.高墩波形钢腹板PC箱梁桥施工期峡谷地形风致响应研究[D].邯郸：河北工程大学，2019.

收稿日期：2020-12-16

作者简介：陈国光（1970—），男，黑龙江拜泉人，高级工程师，主要从事电力系统和风力发电项目前期、基建、运行管理工作。