基于回归神经网络的柴油机NOx排放预测及影响分析
2021-03-08伦智梅张振京宋业栋谢熙顾昕岑
伦智梅,张振京,宋业栋,谢熙,顾昕岑
(1.内燃机可靠性国家重点实验室,山东 潍坊261061;2.潍柴动力股份有限公司,山东 潍坊 261061)
国六排放标准的发布对柴油发动机NOx排放有了更高的限制要求。因此,研究如何准确估计发动机NOx排放值并识别其关键影响因素,对掌握发动机燃烧过程的复杂影响机理、有效采取优化设计是至关重要的。文献[1]基于柴油机台架的重复性试验,分析各参数变化趋势及NOx排放量的相关性;文献[2]探讨了发动机ETC测试时NOx比排放的预测方法,以减少SCR系统标定试验的工作量;文献[3]基于三输入参数的RBF神经网络模型实现了NOx排放预测,为控制柴油机NOx质量流量的排放水平提供了一定的参考。
计算柴油发动机原机NOx质量流量值的传统方法是通过查询标定好的MAP图,获取到某一工况对应的NOx质量流量排放值,该方法具有标定MAP过程相对复杂、计算精度低的局限性,且当发动机工况运行状态发生变化时需重新标定MAP,可能导致台架试验的标定工作量增加;此外,用于标定MAP的参数之间可能存在强耦合的关系。因此,该方法不能准确地表征发动机NOx排放的实际水平,可能无法达到国六排放标准对NOx排放限值的检测要求。神经网络预测方法可以不断学习训练样本特征,具有良好的数据容错性、鲁棒性和泛化能力,目前已广泛应用于各类非线性回归问题[4-5]。本文构建多输入单输出的神经网络回归模型,通过大量试验样本数据特征进行权值训练,从而建立多参数输入的非线性回归映射关系,以实现对NOx质量流量值的精确预测;此外,提出一种影响因子分析算法,分析输入因子对输出参数的影响权重,以期有效识别影响NOx质量流量排放的关键影响参数。
1 数据准备
1.1 影响因素输入变量选取
发动机燃烧是一个复杂的化学反应过程,为了研究影响NOx排放情况的关键因素,本文基于试验过程中积累的先验知识,以冗余的选择原则,选取影响发动机NOx排放水平的12个性能参数作为回归神经网络的参数输入,分别为:发动机转速;轨压测量值、增压压力、进气压力;进气温度、发动机出水温度、SCR上游温度;主喷提前角、主喷设定提前角;预喷油量、总喷油量,空气质量。
1.2 数据获取与预处理
采集同一柴油机型号的多次ETC工况台架试验的试验数据,获取的有效实验数据条数约为180 500条。
为避免各输入参数之间的量纲差异,需对获取的试验数据样本进行归一化处理,以有效消除不同输入参数因单位不统一的影响;同时,选取同型号发动机长期统计得到的极限值,即各参数的最大、最小历史数值作为预处理的基础计算值。
本文采用的归一化算法为线性转换算法,归一化算法的计算公式定义为
(1)
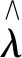
2 神经网络回归模型
2.1 神经网络的回归原理
由于发动机NOx值的影响因素有多个,所以传统的回归方法无法精确地描述自变量与因变量之间的具体函数映射关系,很难拟合准确的函数表达形式;而神经网络结构可包含多层网络层,各层包含多个神经元,且相邻层之间神经元全连接,可同时允许数量足够多的变量作为输入参数,通过对大量试验样本进行特征学习与权值优化,使各层网络的权值参数达到最优状态,最终确定出表征输入与输出目标的非线性函数[6]。当网络训练完成后,其网络结构及参数取值即代表了映射“输入→输出”的映射关系。
本文拟构建的神经网络为多输入、单输出模型,输出值为NOx质量流量排放值;因此,基于神经网络模型结构设计和训练,可以搭建多输入-单输出的映射关系,从而实现预测效果。
2.2 模型构建及训练
回归神经网络基本结构如图1所示,其模型结构除输入、输出层外,还包含两层隐含层。其中,输入层神经元个数等于模型输入参数个数;输出层神经元个数为1,输出结果即为发动机NOx质量流量的预测值。经过多次训练实验,并对比分析模型每次训练结果可知,当隐含层神经元数目为{16,12}时,训练均方误差达到最小。
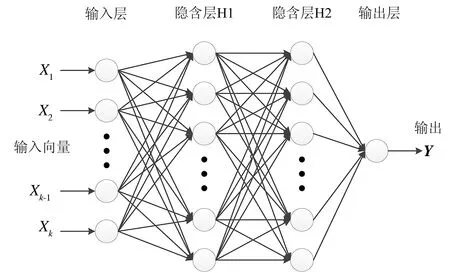
图1 神经网络结构图Fig.1 Neural network structure diagram
模型采用S形对数(Log-Sigmoid)激活函数,其目的在于向多层神经网络中引入非线性,以更好地拟合非线性映射关系。激活函数表达公式为
(2)
式中x是网络模型输入参数。
网络模型训练过程中采用梯度下降法作为学习算法,算法流程如图2所示。训练过程描述如下:
1)初始化网络结构及网络参数权值。
2)以归一化处理后的数据作为训练网络模型的训练样本集,数据集可以描述为(X,Y),其中:X为模型的输入数据向量集;Y为模型的目标输出向量。
3)逐层前向计算,得到神经网络的实际输出值o。对于输出层,实际输出值的计算公式为
(3)
式中:j为输出层的输入层(H2层)神经元序号;wj为H2中第j个神经元节点与输出层节点间的权值。同理,将输出层的神经元yj继续向前转化,即可得到输入层xk与输出值o的表达关系,其中:i为H1层神经元序号;vij为H1层中第i个神经元与H2层中第j个神经元的连接权值;λki为输入层第k个输入参数节点与H1层第i个神经元的连接权值。
4)计算目标输出值y与实际输出值o的误差,本文为单输出模型,则反向误差计算公式定义为
(4)
结合公式(3)与公式(4)计算可得反向误差值,经过循环迭代,反向地逐层调整各层连接权值,直到反向误差值小于设定的误差阈值,或者迭代次数达到设定的最大迭代次数,模型训练过程得以结束,并保存模型为M_net。
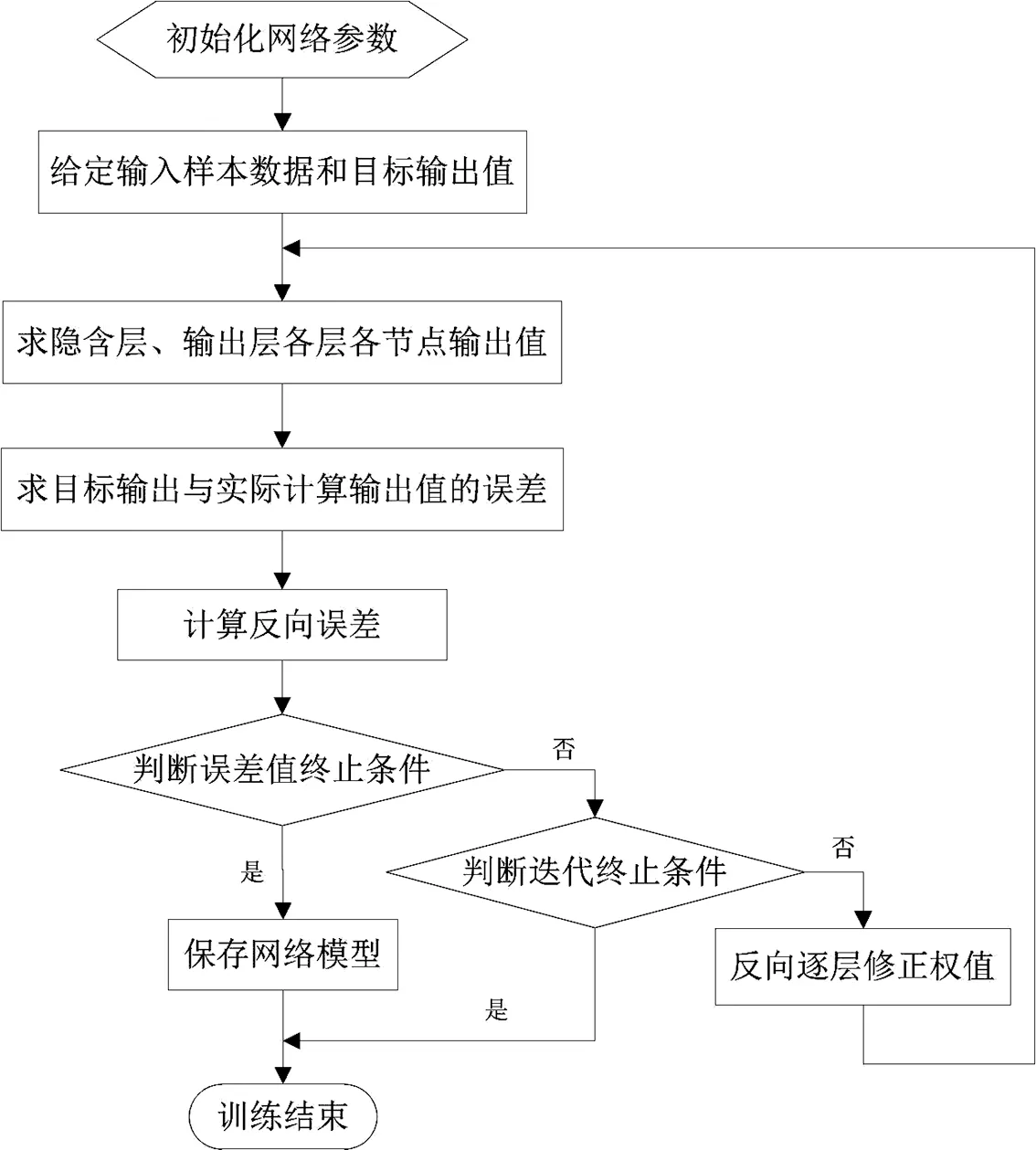
图2 学习算法流程图Fig.2 Flow chart of learning algorithm
通常由均方误差(mean squared error,MSE)来评价神经网络训练质量与模型性能,均方误差值是指参数估计值和参数真值之差平方的期望值,MSE越小,则说明神经网络模型的预测精度越高。MSE的计算公式定义为
(5)
式中:N是测试样本的数目;ti为样本实际值;ai为预测输出值。
在网络训练过程中,网络的均方误差变化曲线如图3所示。当训练迭代1 000次时训练终止,此时网络达到最优,其均方误差值为5.023×10-5。

图3 均方误差变化曲线Fig.3 Mean square error curve
2.3 实验验证及结果分析
为验证网络回归模型预测的精确性,本文选取了另一组实验数据作为测试样本进行测试实验,并对比实际值与模型预测值,对比结果如图4所示。选取横轴区间为[1 000,1 250]的结果曲线放大观察,如图5所示。
利用相对误差计算值来评价神经网络模型的精度,其计算表达式定义为
(6)
式中:ti为NOx质量流量实际值;ai为网络模型输出的预测值。
从图4及其放大图图5可以看出,网络模型预测结果(反归一化处理后)与实际值大致重合,具有较好的逼近预测性能,表明了该回归预测模型具有较好的泛化性能;同时,利用公式(6)计算得出模型预测结果的相对误差基本在5%以下,在实际工程应用的允许误差范围内,满足NOx质量流量的预测精度要求。
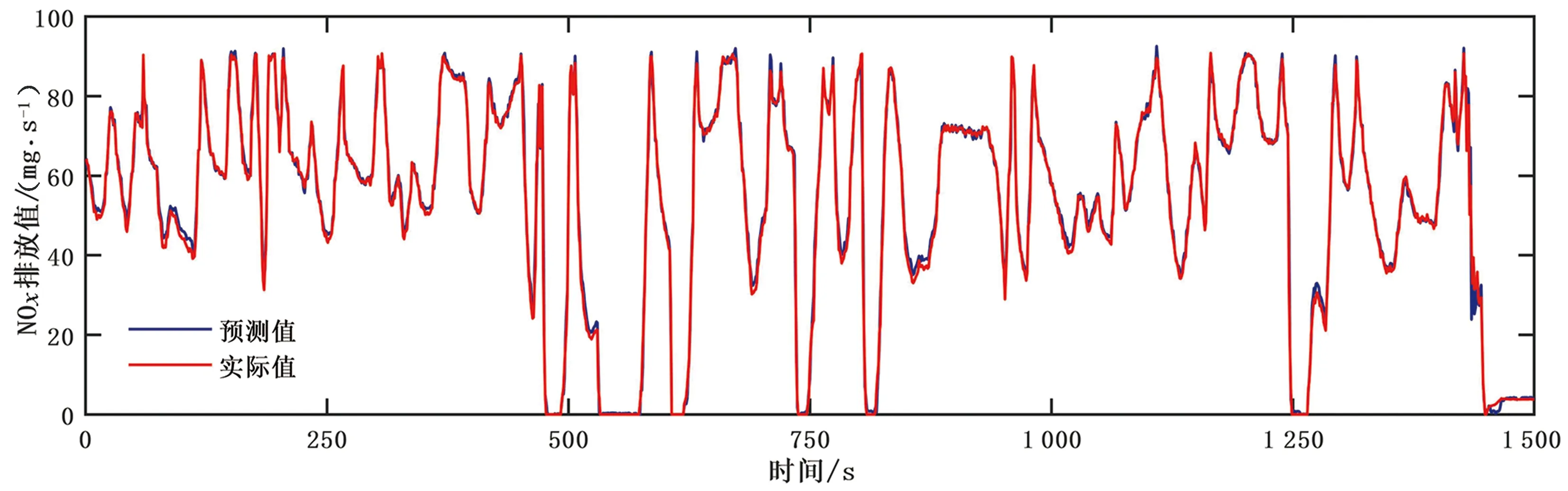
图4 NOx预测值与实际值对比结果(部分数据)Fig.4 Comparison of NOx predicted value and actual value (partial data)

图5 图4中[1 000,1 250]区间的曲线放大图Fig.5 A magnified view of the curve between [1 000,1 250] in Fig.4
3 NOx排放影响因素分析
由于MIV(平均影响值)[7]作为确定输入神经元对输出神经元影响大小的一个重要指标,其绝对值大小定量地表征了影响的相对权重;因此,本文考虑在神经网络模型的基础上,采用MIV算法来评价各输入变量的相关性,并衡量各输入变量对输出变量的相对影响权重。
3.1 MIV影响因子分析算法
MIV算法流程如图6所示,实现步骤如下:

图6 MIV算法流程Fig.6 MIV algorithm flow chart
1)设定MIV的调节率Ki,即各输入变量变化的比例,其中i为调节率的序号。
2)模型训练样本的每一自变量值在其原值Po的基础上分别增加和减少当前调节率的比例大小,得到新的训练样本数据集Pi_max、Pi_min。
3)针对每一自变量,以调节后的新训练样本数据Pi_max、Pi_min分别作为该自变量的测试样本数据,用已训练好的神经网络模型M_net进行仿真测试,并得到两组预测结果Ri_max、Ri_min。
4)计算各个自变量的两次预测值之差,即为IVi值,其物理意义为:按一定比例调整该自变量大小时,可以改变模型输出结果产生的影响大小。
5)计算IVi值的均值,即该自变量对于网络模型输出目标变量的MIVi值。
绝对值|MIVi|的大小可以衡量对应输入变量对输出变量的相对重要性与影响权重,也可基于相对影响权重值,剔除权重较小的输入变量,以便重构和优化训练模型,实现对网络输入参数的降维,进一步降低网络模型的复杂度。
本文设定4个MIV的调节率,分别为K1=10%、K2=15%、K3=20%、K4=25%。同时,针对每一个调节率,做多次测试实验,组内求均值后最终计算得出各变量的MIV绝对值,结果见表1。
3.2 NOx排放影响因子分析
根据各变量的|MIV|计算结果,绘制出各调节率下不同影响因子的|MIV|值变化曲线及其标准差柱形图,如图7、图8所示。

表1 各输入变量的|MIV|值Tab.1 |MIV| value of each input variable

图7 各影响因子的|MIV|值变化曲线Fig.7 The change curve of |MIV| value of each influence factor

图8 |MIV|标准差柱形图Fig.8 Standard deviation bar chart of |MIV|
由图7可以看出,在不同调节率下,主喷提前角、转速、总喷油量、主喷设定提前角、空气质量5个输入变量对发动机NOx质量流量排放的影响权重相对较大;而温度类变量,如SCR上游温度、发动机水温、进气温度对NOx排放水平的相对影响权重几乎为零,可以忽略;其它输入变量对NOx排放值的影响相对较小。不同调节率的权重变化曲线走势基本保持一致,仅在不同调节率下各输入参数对NOx的影响程度略有不同。由图8可知,主喷提前角、主喷设定提前角及总喷油量3个输入变量的|MIV|标准差较大,即随着调节率的变化,以上3个参数的变化最为灵敏,其敏感度相对较高。
为了更加清晰地表达各影响因子对NOx排放值的影响权重占比情况,绘制了图9所示的|MIV|权重占比图,各柱形分别代表各自的影响权重占比。由图9可以看出,在不同调节率下,主喷提前角在所有参数中的权重占比最大;其次,转速、主喷设定提前角及总喷油量占较大的权重百分比。综上得出,影响发动机NOx排放水平的主要因素包含了以上4个参数。
此外,主喷提前角、主喷设定提前角两输入参数的|MIV|权重占比随调节率的增大而增大,所以,这两个变量与NOx排放值呈正相关关系,其它输入变量均为负相关关系。因此,NOx排放的影响因素不是单一的,而是受多种因素综合影响。

图9 各影响因子的|MIV|权重占比Fig.9 |MIV| weight proportion of each influence factor
4 结束语
本文构建了多个输入与单输出目标之间的非线性回归神经网络,并基于测试数据进行模型验证。验证结果表明,模型实际预测值与期望输出值的相对误差在5%以下,验证了该神经网络回归模型具有较高的预测精度与泛化性能,精确地拟合了多参数与发动机NOx排放量之间的复杂映射关系,实现了对发动机NOx质量流量排放值的准确预测。基于已构建的网络回归模型,采用MIV算法定量分析了各输入参数对发动机NOx排放量的影响权重相对大小。计算结果表明,在模型输入变量范围内,主要由主喷提前角、发动机转速、主喷设定提前角及总喷油量4个关键影响因素综合影响发动机NOx质量流量的排放量。本文提出的影响因子分析算法可为后续实现控制发动机NOx排放要求提供有力的理论依据,同时为网络模型输入的降维、迭代与优化提供了重要依据。
