AUV水下移动重力测量建模及误差分析
2021-03-08张志强于瑞航崔银锋
张志强,于瑞航,崔银锋
(1.武汉大学 测绘学院,湖北 武汉 430079;2.海军工程大学 兵器工程学院,湖北 武汉 430033;3.国防科技大学 智能科学学院,湖南 长沙 410073;4.中国人民解放军 陆军特种作战学院 机电工程系,广东 广州 510502)
0 引言
准确感知海洋地球物理信息是认知海洋的首要前提。而对于海洋重力数据研究来说,其在地球物理、矿产资源勘探、军事运用、弹道导弹发射等方面均有广泛应用,是海洋地球物理信息中至关重要的一部分,尤其在探测海底矿藏方面,重力测量是得到地下结构剖面的有力工具和矿产资源勘探的有力手段[1-3]。尽管卫星测高和船载重力测量获得的重力数据能解决数千米乃至更大区域的重力特性问题[4-6],但较小规模的地质特征,例如亚公里空间波长的地质特征,仍需辅以水下和近海底调查,克服离势场源过远所造成的信号衰减问题。
水下移动重力测量,也就是在靠近海底的移动平台上使用可连续记录的重力仪,能够大大增加重力测量的次数和空间覆盖范围。因此,在一些情况下,如热液矿床测量,既要保证一定的分辨率,又要确保探测区域和效率,采用水下移动重力测量是最佳手段。水下移动重力测量主要采用拖曳式和自航式。拖曳式水下移动重力测量方面,Zumberge开发了一种拖曳式海洋重力测量系统 Towdog[7],它在海底上方大约30 m高度拖曳,具有0.1 mgal的精度。使用拖曳方式实施重力测量解决了连续水下重力测量问题,但其需要庞大的作业母船进行保障,而且还存在拖鱼与水面母船运动耦合、难以保持安全高度以及水下操纵能力有限等不足。自航式水下移动重力测量方面,随着自主水下无人航行器(Autonomous Underwater Vehicle,AUV)越来越多地用于海洋测量及调查工作,许多以前由拖曳系统、HOV和ROV进行的地球物理测绘任务,包括多波束测深、磁力测量等,改由 AUV完成。如Purcell使用3台REMUS 6000型AUV快速调查了较大海域的深海海底,成功寻找到了法国航空公司447航班的残骸[8]。AUV由于是自主控制、无拖缆的水下航行器,能够明显减轻水面母船的作业压力,允许水面母船同时执行多个任务,进而降低了水下重力测量相关的高昂成本和准入门槛,是理想的水下移动重力测量平台。
当前不同功能定位的AUV平台快速发展,以此为基础,本文提出利用当前发展比较成熟的AUV平台,搭载相关测量设备进行水下重力测量的思路,该方法摆脱了以往水下定点重力测量或拖曳重力测量的局限与不足,为深海资源勘察、军事目标探测等任务提供技术支撑,这也是深远海研究中一个非常重要的热点研究方向。
进行水下移动重力测量的理论难点是测量误差的分析,相对于常见的航空、船载移动重力测量,水下移动重力测量主要存在2个方面的问题:1)水下无法使用卫星定位信号,需要使用水声定位、捷联惯导以及深度计等多种辅助定位设备才能得到准确三维位置信息;2)水下航行物体运动姿态与飞机、舰船航行有较大区别,对于重力测量的影响机理不同。本文介绍了水下移动重力测量的相关基础知识,推导了水下移动重力测量情形下重力扰动计算公式,分析了捷联重力仪水下测量误差的特性。
1 水下移动重力测量基础理论
水下航行物体搭载重力仪在水下按一定航线航行,由牛顿第二运动定律可知,惯性系中质点运动方程可以表示为[9]

由式(1)得到:

式(2)是水下移动重力测量的基本原理,即利用牛顿第二定律,将地球引力加速度从动态测量值中分离出来,其中包括了载体加速度。由广义相对论的等效原理可知,加速度和万有引力的作用是等效的,因此不能使用加速度计对重力直接进行测量。
进行水下静态重力测量时,由于测量设备处于静止状态,其载体加速度为=0,因此,通过对重力传感器敏感轴的空间指向(垂直水平面的方向)进行调整就能够测得重力加速度。水下静态重力测量的测量精度可以很高,能够达到地面测量的精度水平,水下静态的测量深度可达km量级,但这种水下逐点依次测量的方式效率比较低下,不能满足大范围内水下重力测量的作业需求。为解决水下静态重力测量效率低、覆盖面小的问题,需要考虑采用水下移动重力测量方法。
水下移动重力测量的过程中,设备处于不断运动状态,因此加速度不再为0。此时,重力传感器测得的结果同时包含重力加速度和载体加速度,并且这两种加速度无法区分。因此,对移动重力测量进行研究时迫切需要解决2方面问题:1)解决在运动状态下,如何让传感器的敏感轴保持稳定的指向;2)载体加速度与引力加速度如何进行有效分离。
对于第1个问题,主要有3种方法:1)利用周期性阻尼和以陀螺为主的惯性传感器组成惯性稳定平台,维持测量设备的稳定垂直指向和水平基准,如美国 Lacoste & Romberg重力仪;2)采用舒勒调谐平台,以消除水平加速度对重力传感器测量输出的影响,这类设备以俄罗斯 GT系列重力仪和加拿大AIRGrav重力仪为代表[10];3)采用“数学平台”,通过计算载体坐标系与当地地理坐标系的姿态转换矩阵,将重力传感器测量值投影到相应坐标系下,一般被称为捷联式惯性稳定平台[11]。
对于第2个问题,主要有2方法:1)将共基线的2个加速度计测量得到的结果求差,旨在消除运动载体因共有运动所产生的误差。在共用基线可以保持稳定的运动状态且可以旋转的条件下,对其做差可以从差值中分离出相应的重力梯度分量,这就是重力梯度测量的基本原理。但梯度测量设计的技术方法和对硬件要求相当苛刻,实现难度很大。2)使用2种不同且独立的测量方法,要求由一种方法得到的测量值含有引力加速度信息的比力观测值;另一种方法得到的测量值只包含载体加速度,同一坐标系下做差,就能够得到重力加速度。现阶段,有卫星应用条件下的重力测量方法大多采用差分卫星定位(DGNSS)技术来求解载体加速度,进而实现重力加速度的分离。而对于水下重力测量来讲,卫星导航系统GNSS不可用,因此需要引入新的测量方法。
通过上述分析可知,使用AUV开展水下移动重力测量需要3个组成部分:第1为重力传感器分系统,该部分包括获取比力的重力仪或加速度计;第2为平台分系统,使加速度计保持水平或计算其姿态;第3为定位分系统,主要用于得到AUV的惯性加速度。典型AUV重力测量系统如图1所示,这是日本海洋科学与技术中心(JAMSTEC)的URASHIMA型AUV搭载的重力测量系统,其重力仪为 Lacoste公司的动态重力仪 S-174,平台分系统为惯性三轴陀螺平台,定位分系统由多普勒计程仪(DVL)、惯导、深度传感器、超短基线水声定位装置以及母船搭载的差分 GPS组成,母船和AUV之间采用水声技术进行通信。
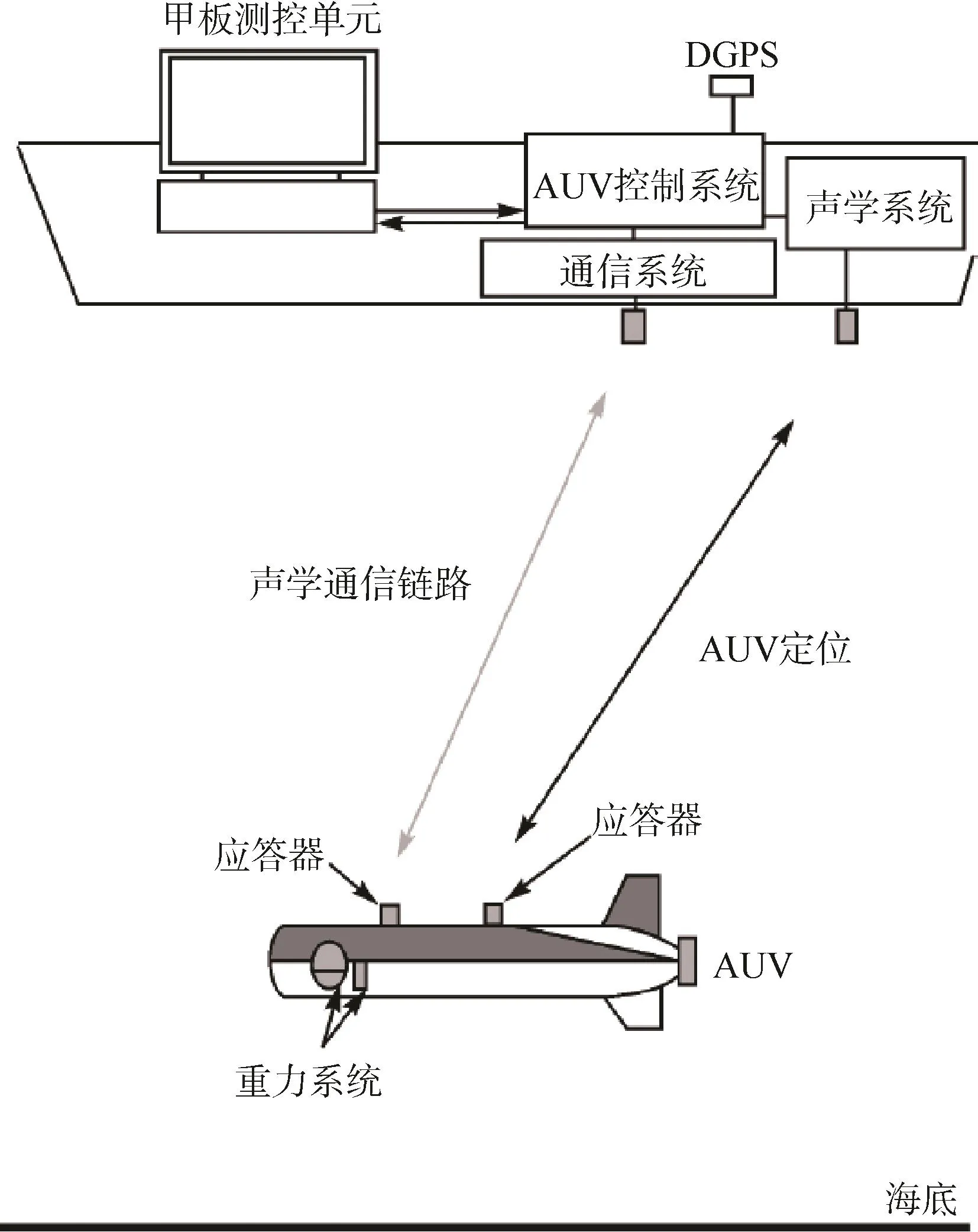
图1 典型AUV重力测量系统Fig.1 Typical AUV gravity measurement system
AUV重力测量按照测量结果可以分为标量、矢量、梯度重力测量3类,常见的重力测量为标量重力测量。按照使用的平台分系统可以分为平台式、捷联式、旋转不变式3类。标量重力测量可以使用3种平台分系统中的任何一种,平台式使用了精密加速度计,捷联式使用了数字平台,旋转不变式使用三轴加速度计。矢量重力测量主要使用平台和捷联式。梯度重力测量使用旋转不变式平台分系统进行测量。
2 水下移动重力测量数学模型
由上述分析可知,水下移动重力测量的基本原理是利用牛顿第二定律,将地球引力加速度从动态测量值中分离出来,进而得到导航坐标系下的移动重力测量模型。依据AUV搭载传感器特点以及建立的动态重力测量模型,可以分析相应重力测量的误差特性。
结合当地的地理导航坐标系内部机械编排可知,导航坐标系下地速Ven的变化率可通过在惯性坐标系下的变化率得到[12]:

式中:ωie为相对于惯性系的地球自转角速度;ωen为相对于导航系的相对转动角速度。
另一方面,惯性系下的速度变化率可以表示为
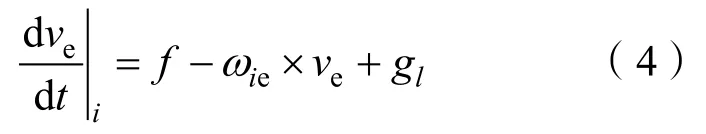
式中,gl为当地重力矢量。
将式(4)代入式(3)中,得:

其在导航坐标系中表示为
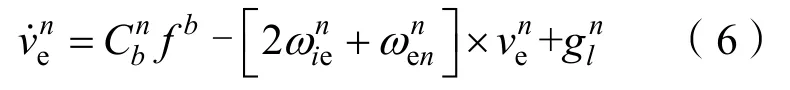

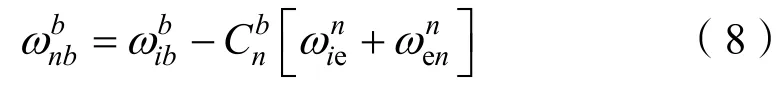
将式(6)的重力值移到等式左边,于是,移动重力测量的表达式在导航系下可以表示为
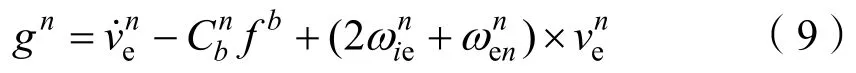
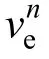
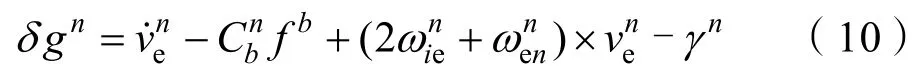

式(10)是矢量表达式,通过计算可以得到重力的3个分量表达式:
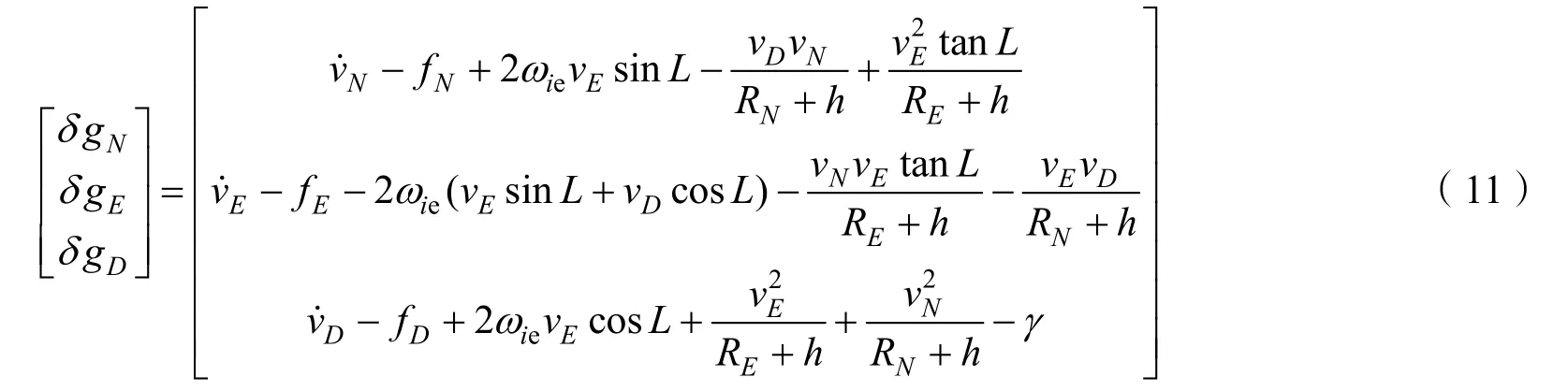
式(11)中的第3个分量就是标量重力测量的基本原理:
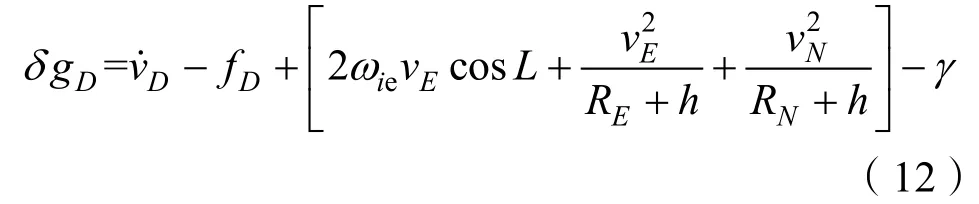
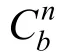

正常重力γ与所在纬度L、高度h等位置信息相关:


式中,g0(L)为地表重力:
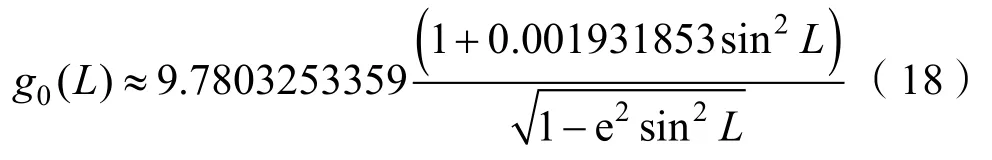
综合以上分析,高精度的载体信息,如位置、重力仪姿态、速度、加速度等是得到高精度扰动重力计算值的基础。此外,需要在水下重力测量过程中进行误差估计并对误差进行补偿。
3 水下重力测量误差分析
由扰动重力矢量计算公式即式(10)可以得到水下移动重力测量的误差模型:


3.1 姿态测量误差
由式(19)可知,比力测量误差还与捷联惯导系统姿态测量误差ψ有关。
对式(19)右边第1项进行展开,可得:
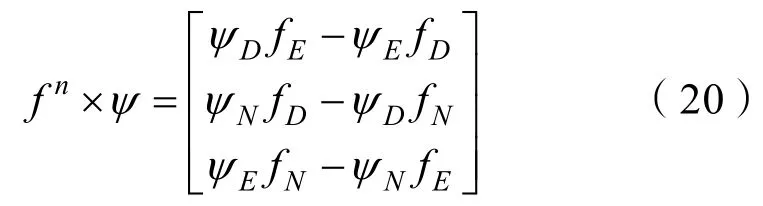
由式(20)的前2个分量可知,重力的北向和东向 2个水平分量受姿态误差影响较大。水平姿态出现误差,水平分量测量误差就会达到约4.7 mgal,由式(20)的最后1个分量可知,水平加速度对重力测量精度也会产生较大的影响。但对于标量重力测量来说,姿态测量精度根据不同长度的滤波周期,可以相对放宽10"以上。
3.2 位置测量误差
载体位置测量误差主要引起2个方面的计算误差,即离心加速度和哥氏加速度的计算误差和正常重力的计算误差。
导航系下位置误差引起的离心加速度和哥氏加速度计算误差为[13]
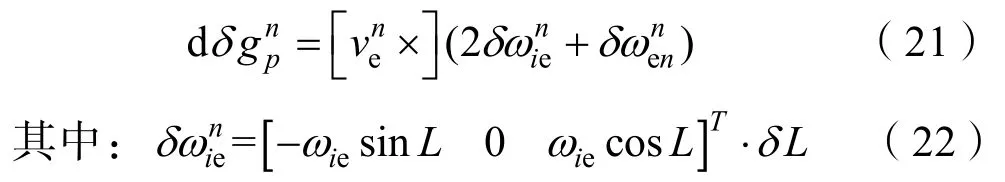
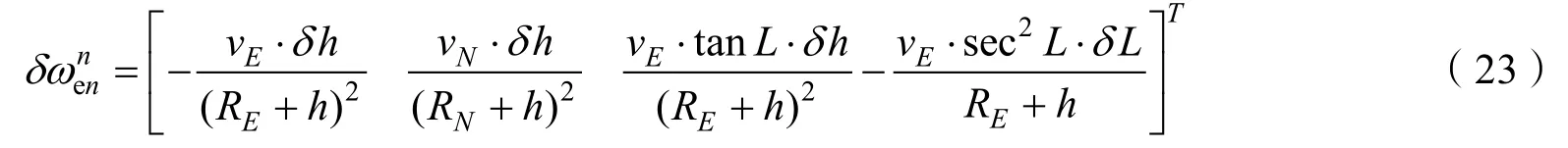

对于水下重力测量来说,主要使用水声定位方式对AUV、ROV等水下航行器实施主动定位,包括超短基线水声定位、短基线水声定位以及长基线水声定位系统等。常用的超短基线水声定位系统精度可以达到测量斜距的0.5%以内,如我国“蛟龙”号深潜器配套的超短基线定位系统,在环境噪声为60 dB时最大作用距离为8 000 m,在60°圆锥角内时测距精度为 0.3%斜距,最大工作水深达到7 000 m[14]。以水下500 m水深的重力测量为例,超短基线定位误差可以控制在0.3 m以内,因此完全满足上述对位置精度的理论要求。
正常重力的计算误差与高度和纬度相关,正常重力对高度求偏导数,有:

所以,对于水下重力测量来讲,1 m的深度测量误差将引起0.3 mgal左右的误差。而目前深度计的测量精度可以达到 5 cm,因此,正常重力的计算误差小于0.02 mgal,满足水下重力测量对位置、高度等定位精度要求。
3.3 速度测量误差
速度误差引起的离心加速度和哥氏加速度计算误差为

计算表明,当速度误差在0.1 m/s时,速度产生的误差主要是厄特弗斯校正误差,可达mgal级。因此,速度测量精度比较关键。
由于水下有多普勒计程仪(DVL)可以提供速度测量信息,在对底跟踪的条件下,目前常用的多普勒测速仪速度误差低于 0.1 m/s,因此可以满足水下重力测量对速度的精度要求。
3.4 其他误差
载体运动加速度的测量精度决定了重力测量精度和分辨率,在航空重力测量以及海洋重力测量的过程中,利用全球卫星导航定位系统(GNSS)求解的载体加速度精度可达mgal级。而在水下重力测量中,无法直接利用GNSS提供精确的位置信息求解加速度信息[15],因此需要其他方式如超短基线水声定位系统(USBL)、多普勒计程仪(DVL)、惯导和深度计为水下重力仪提供定位信息。对于垂直方向上的载体加速度,深度计测得的深度信息相比水声定位系统精度更高,因此,垂直方向的载体加速度信息主要由深度计数据计算得到。如果获得的信息含有大量噪声,则需要采用低通滤波的方法将高频部分的噪声滤除,以提高加速度测量精度。
捷联惯导系统与其他分系统如多普勒计程仪、深度计、超短基线等设备的量测值存在时间同步的时间误差和安装杆臂的空间误差。对于时间同步误差,在典型的动态环境下,时间同步误差为 1 ms时重力测量误差会达到20 mgal,因此必须将时间同步误差降至50 ns以内,这样才有可能使测量精度达到1 mgal内[16]。
4 结束语
本文通过研究船载和航空重力测量,推导了基于捷联式重力仪的水下移动重力测量模型,将地球引力加速度从动态测量值中分离出来,分析了移动重力测量中需要解决的稳定重力传感器敏感轴以及分离载体加速度两个问题。在此基础上以典型AUV水下重力测量为例,说明了水下移动重力测量所需的重力传感器分系统、平台分系统和定位分系统。
由于水下移动重力测量涉及惯性坐标系、地固坐标系、导航坐标系以及载体坐标系的相互转换,介绍了这几类常用坐标系,说明了方向余弦矩阵、欧拉角和四元数的转换关系。接着推导了导航坐标系下的移动重力测量模型和误差模型,重力测量值可以由比力、方向余弦矩阵、载体位置、速度和加速度测量值计算得出,其中比力测量值和方向余弦矩阵可以由惯性器件输出的测量信息和惯性导航解算得到,载体位置、速度和加速度则需要由专门的水下导航定位设备得到。分析了捷联重力仪安装在AUV上实施测量时的误差特性,推导了基于捷联式重力仪的水下移动重力测量误差模型,研究了重力传感器、姿态测量、位置测量、速度测量以及其他测量手段带来的误差。根据水下移动重力测量特点,结合水下导航定位设备特点和性能,讨论了达到1 mgal测量精度的可行性以及对水下定位设备的性能要求。经计算,在重力传感器与捷联式航空重力仪一致,水声定位系统定位精度达到测量斜距的0.5%,水压深度计测深测量精度达到5 cm,多普勒计程仪测速精度达到0.1 m/s的情况下,可以确保水下移动重力测量达到精度要求。
