先后掘进盾构间距对下穿既有立交桥桩基影响分析

冯 勇 （中铁十六局集团北京轨道交通工程建设有限公司，北京 101100）

1 引言

伴随城市的发展，市内交通拥堵日趋严重，目前解决城市交通拥堵现象的主要方法是修建地铁与高架，两者大都在不同的时期建设，且高架建设大都早于地铁建设。后期建设地铁对前期建设的高架难免产生影响，甚至影响其安全运行，对其结构安全进行分析非常必要。

R.B.Peck通过对单孔隧道施工所产生的地表沉降数据进行研究，提出地表沉降凹槽近似于正态分布曲线；1975年，刘建航院士通过对上海地铁监测数据进行研究分析，提出了“欠地层损失”概念，并对Peck公式进行了修正。2002年Mroueh和Shahrour等人根据地铁经过单桩和桩群基础引起的偏移量和沉降量，运用数值计算方法进行分析研究，他们提出随着盾构的推动，桩基的弯曲力矩和剪切应力都将得到增加，并且桩基的位移量和竖直应力也会随着桩身与隧道之间的水平和纵向间距的变化而发生变化。2011年张恒、陈寿根等对隧道盾构下穿公路立交桥分析，发现桩基主要是水平方向上的变形，并且上半部分朝向隧道一侧，下半部分背离隧道一侧。

2 模型建立

2.1 模型概况

本文以合肥地铁2#线下穿五里墩立交桥为研究对象，并选取其相关数据建立数值模拟模型，依据圣维南计算原理，规定左、右隧道轴线向外5D（D为隧道直径）距离作为此模型的X轴，距离为78m；规定沿隧道轴线方向作为模型的Y轴，长度为60m；规定竖向作为模型的Z轴，长度为45m。土体厚度为39m，拱顶至地表取其覆土厚度为25.5m；盾构掌子面直径为6.28m；模型选取宽度为1.5m厚度为0.3m的管片；注浆层厚度为0.14m。立交桥桥桩长度为16.5m，桩径1.2m，桩体与拱顶距离为7.5m。左隧道与右隧道中心相距18m，左桩体中心在两隧道之间三分之一位置处，距左侧隧道中心线12m；右桩体中心距右侧隧道中心线为9m。隧道与桩体相对位置如图2所示。

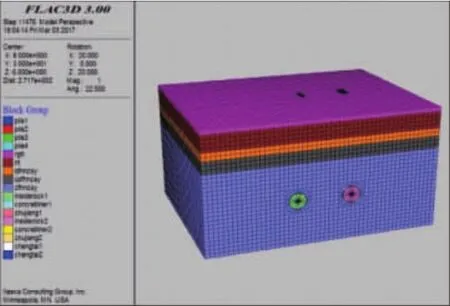
图1 有限元建立的数值模型

图2 盾构区间隧道与桩基的位置关系图

2.2 模型参数

依据地质勘查报告的相关数据，确定所建立模型中的地层分布自上而下分别为：人工土覆盖层、粘土层、全风化泥质砂岩层、强风化泥质砂岩层及中等风化泥质砂岩层，厚度分别为1.2m、5.9m、2.1m、4.7m、24.5m。采用实体单元来进行有限元数值模拟。土体选用M—C本构模型，管片、桩基、承台和注浆均选用线弹性本构模型。盾构掘进过程利用FLAC进行数值模拟，按掘进顺序激活管片和注浆体，其中注浆凝固可分为两步骤进行，开始注入浆体时候，浆体弹性模量较小，往后随着浆体的凝固，浆体弹性模量逐渐增加。由于存在微小裂缝，混凝土实际值与理论值存在一定误差，故取实际弹性模量的90%作为理论计算值，均设31.5GPa。

材料物理力学参数见下表。

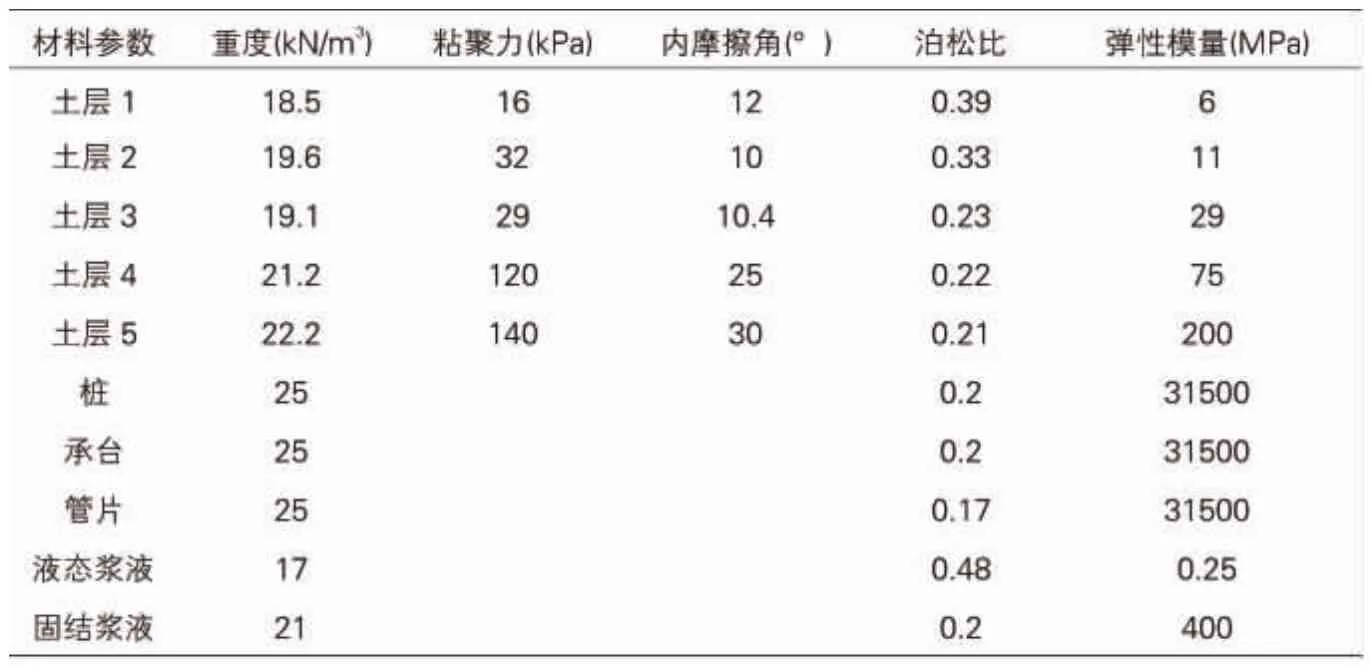
材料参数表

2.3 接触面作用

桩—土接触面分成若干个三角形单元，由两个三角形单元构成四边形单元，继而组合成接触面。桩—土接触面如图3所示，接触面法向刚度与剪切刚度由下式求解得出：

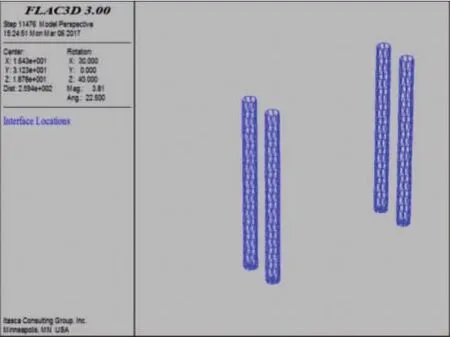
图3 桩—土接触面的模型示意图

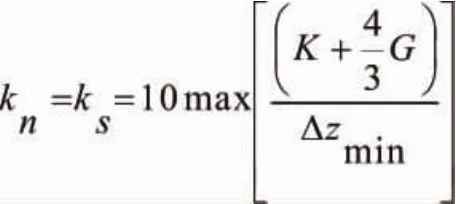
K—体积模量

G—剪切模量

ΔZ—接触面最小连接尺寸

体积模量和剪切模量可根据下式计算得出：

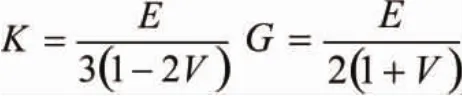
E—弹性模量

V—泊松比

桩土接触面参数中，粘聚力c和摩擦角φ的取值为桩基周围土层相关参数的0.7倍，桥墩自重和桥板承受荷载取为1800kN。

3 数值模拟结果分析

滞后距离分别设定为 0m、12m、24m、36m和60m，根据五种工况进行分析对比。

3.1 滞后距离对水平位移影响分析

1-4号桩基的水平侧向位移，如图4～图7所示。

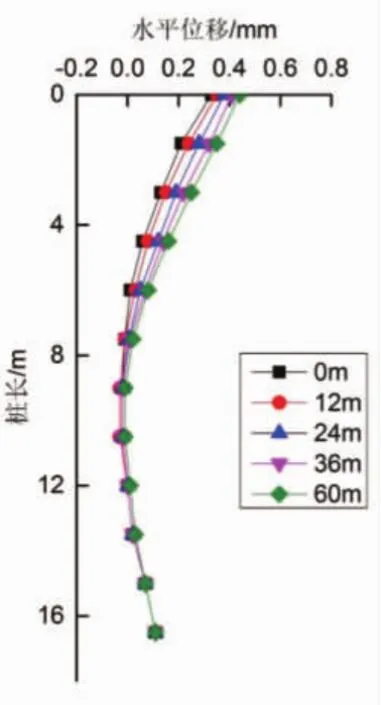
图4 桩1在各种滞后距离下的桩身水平位移

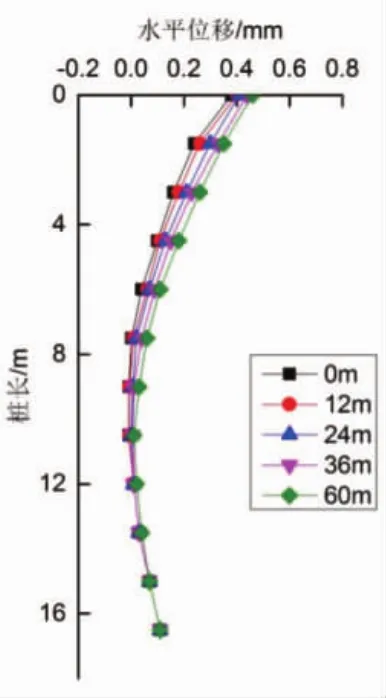
图5 桩2各种滞后距离下的桩身水平位移

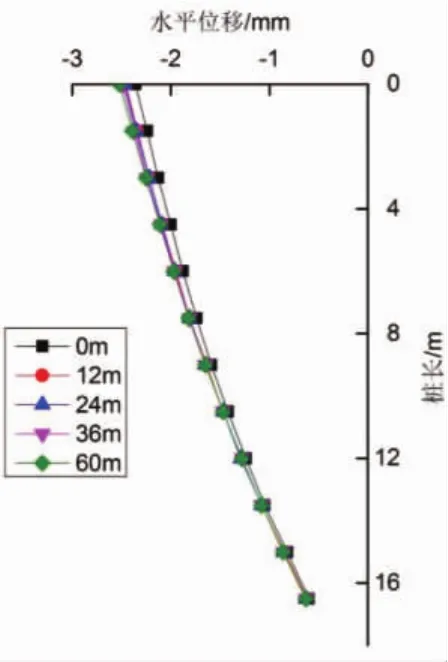
图6 桩3在各种滞后距离下的桩身水平位移

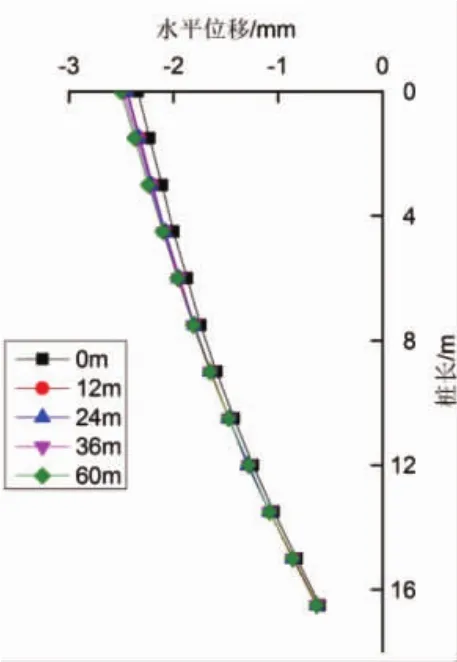
图7 桩4在各种滞后距离下的桩身水平位移

由图4～图7可以看出：在0～60m各种间距下桩身的水平变形规律基本一致，右线先行掘进，且距离桩基较近，隧道掘进造成桩基一侧侧压减小，四个桩基水平位移基本是向先行隧道偏移的。桩1、桩2下部分距离先行隧道仅为2.3m，受土层扰动及损失率影响，桩身附加弯矩和轴力增加，导致桩1、桩2自桩顶向下到2/3桩长范围之间水平位移逐渐减小，而自2/3桩长到桩段，其水平位移变形量逐渐增加。桩1、桩2的桩顶水平偏移量与滞后距离呈正相关，其水平位移增加约27%；而桩3、桩4水平位移仅增加约6.8%。

3.2 间隔距离对竖向位移影响分析

1、2、3和4号桩基的竖向位移，见图8所示。

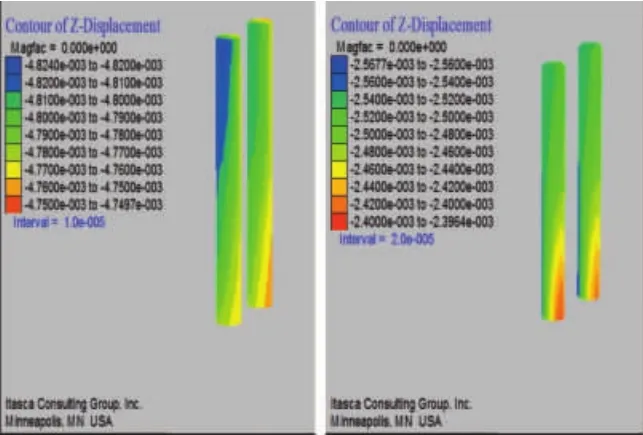
图8 桩1、2和桩3、4在距离0m 时每根桩基竖向位移变化云图

图8～图13中可得出：在五种工况下，四个桩基的桩顶沉降变化趋势基本相同，盾构开挖桩底引起了少量的挠曲变形，导致桩顶的竖向位移比桩底的竖向位移略微偏大；随着间隔距离的增大，桩顶部沉降有所降低，超过6倍桩径后沉降趋于稳定，桩1、桩2的沉降减小约28%，桩3、桩4减小约5%；在滞后距离为60m时，桩1～4的桩顶沉降量分别为 3.50mm、3.43mm、2.42mm和2.40mm。

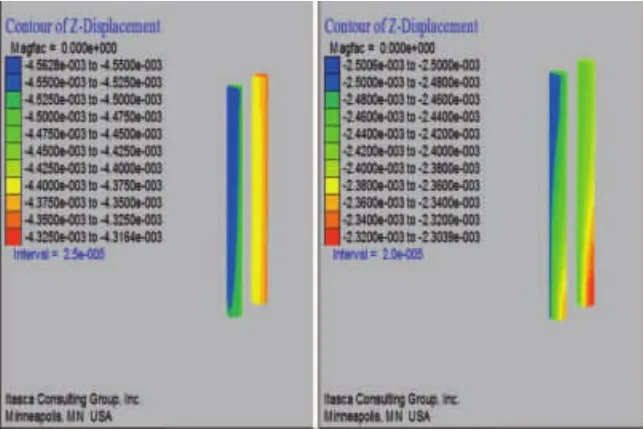
图9 桩1、2和桩3、4在距离12m 时每根桩基竖向位移变化云图

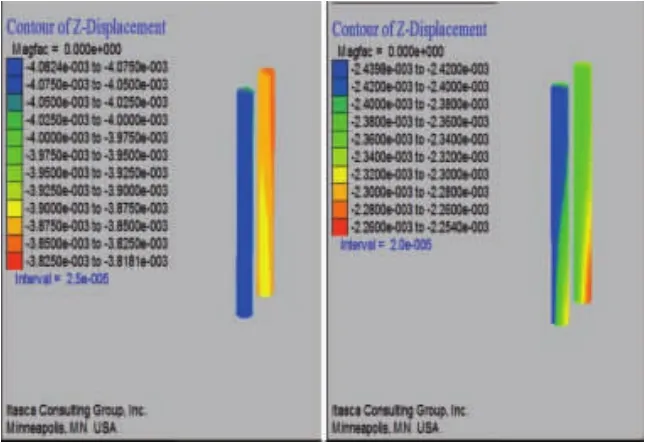
图10 桩1、2和桩3、4在距离24m 时每根桩基竖向位移变化云图

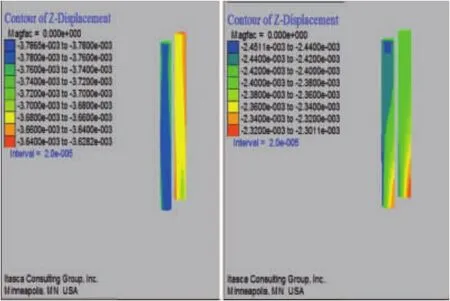
图11 桩1、2和桩3、4在距离36m 时每根桩基竖向位移变化云图

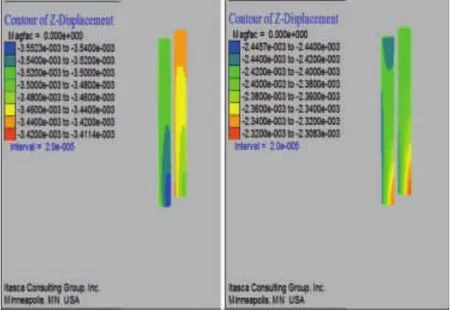
图12 桩1、2和桩3、4在距离60m 时每根桩基竖向位移变化云图

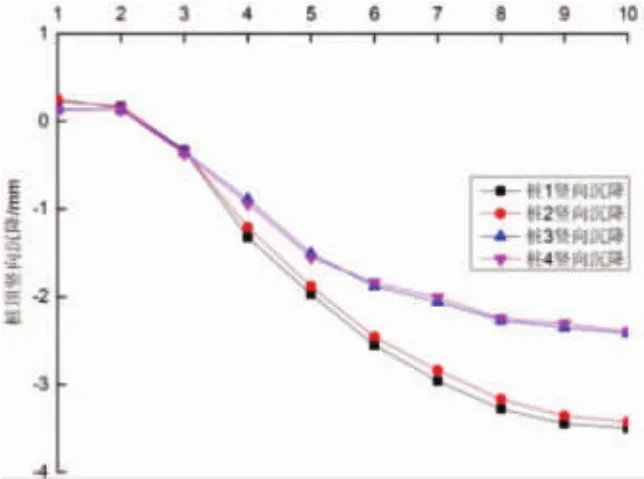
图13 距离60m时桩顶竖向位移变化曲线

3.3 间隔距离对地面沉降影响分析

在Y=30处地表各监测点沉降变化如图14所示，从图14可以看出，地表沉降曲线为“W”形。随着间隔距离的增加，先行隧道的地表沉降不断减小，后行隧道的表面沉降程度相对较小。在先行线和后行线隧道开挖的整个过程中，对地面沉降的主要危害范围分别是中线两侧的3D和2.25D。多线隧道关键危险区的沉淀池容积约占沉淀池总容积的3/4。左右线间距为60m时，先行线隧道中心最大沉降量和后行线隧道中心最大沉降量3.18mm、3.01mm；不同间隔距离下先行线隧道中心位置地表沉降要比后行线隧道约大6%～17%。先行线隧道的表面沉降最大值位于两个隧道中间的桩基右侧，距离约0.25D处，并且靠近先行开挖隧道的侧面。

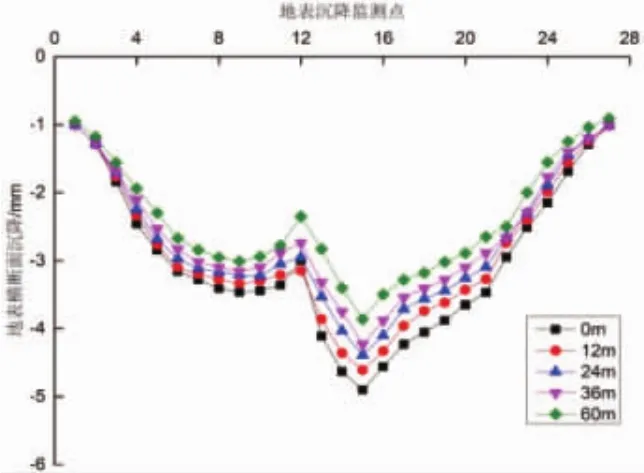
图14 Y=30m处地表横断面各监测点纵向沉降变化图

4 结论

通过分析可以得到以下主要结论。

①不同盾构掘进间隔距离，高架桥桩基水平变形规律基本一致，右线先行掘进，且距离桩基较近，隧道掘进造成桩基一侧侧压减小，四个桩基水平位移基本是向先行隧道偏移的。

②由于桩1和桩2下部分距离先行隧道净距仅为2.3m，土层受到扰动，损失率产生变化后，桩身附加弯矩和轴力增加，进而导致桩1和桩2自桩顶向下到2/3桩长范围之间水平位移逐渐减小，而自2/3桩长到桩段其水平变形逐渐增加。桩1、桩2的顶部水平偏移量与桩间距的大小呈正相关，其水平移动距离增加约27%；而桩3、4水平方向位移仅增加约6.8%左右。

③盾构开挖桩底产生极小的挠曲变形，从而会导致桩顶的竖向位移比桩底的竖向位移略微偏大；随着间隔距离的增大，桩顶部沉降有所降低，超过6倍洞径后趋于稳定，桩1和桩2的沉降减少约28%，桩3和桩4减少约5%。

④表面沉降曲线为“W”形，并且表面沉降量与间隔成反比。在隧道开挖的整个过程中，破坏地面沉降区域的关键是中心线的两侧，即3D和2.25D左右。在不同距离下，先行线隧道中心的地表沉降量比后行隧道大6%～17%。先行隧道的地表沉降最大值位于两条隧道之间的桩基右侧，距离约为0.25D，且靠近第一个基坑的隧道开挖侧面。