基于遗传算法-反向传播神经网络的径向式导叶多级泵水力性能优化

2021-03-07王延锋张连军段海鹏

科学技术与工程 2021年4期

王延锋, 张连军, 段海鹏

(1.中国矿业大学(北京)机电与信息工程学院, 北京 100083； 2.安标国家矿用产品安全标志中心有限公司, 北京 100013； 3.中煤科工集团唐山研究院有限公司, 唐山 063000)

径向式导叶多级泵已逐渐成为大水矿井和超深矿井的矿井水排放与处理的主要设备[1],其水力性能的优劣直接决定着泵内流特性与外特性。但由于多级泵流道结构复杂,具有狭长且窄的特点,内部流动机理尚未被完全了解,导致水力性能优化设计经历设计-试制-试验-改正的反复修正过程[2],优化指导方法仍然处于半经验与半理论的阶段,使得径向式导叶多级泵水力性能的预测准确度不够,严重制约着高效水力模型的研发效率。因此,研究径向式导叶多级泵水力性能预测模型对提高其效率、缩短研发周期具有重要的意义。

随着理论基础、数值模拟和试验技术以及优化算法的发展与提升,针对离心泵水力性能优化设计的研究已成为众多学者的研究目标之一,不同的离心泵水力性能优化设计方法展现了不同的优化设计特点。目前众多学者针对离心泵水力性能优化设计方法的研究主要包括速度系数优化设计[3-5]、损失极值优化设计[6-7]、基于计算流体力学(computational fluid dynamics,CFD)优化设计[8-10]及基于CFD数值模拟与智能优化算法的优化设计[11-13],其中速度系数方法和损失极值法在离心泵水力设计领域应用较多,但该方法受到现有模型和经验系数的限制,无法从根本上提高泵的水力性能,在离心泵水力性能优化设计方面很难取得突破性进展[14-16]；基于CFD的优化设计方法称为从正问题出发的反问题优化设计方法,虽然目前已有众多相关研究成果且取得了良好的设计效果,但由于离心泵过流部件几何参数较多,对泵性能的影响与作用机理各异,能否准确地把握过流部件几何参数与泵性能的关联关系需要反复的数值模拟计算与充分的工程实践经验[17]；而基于CFD数值模拟与智能优化算法的优化设计方法是基于CFD数值模拟计算结果,结合基本流体理论,利用粒子群算法[18]、遗传算法[19-20]和支持向量机[21]构建优化设计数学模型或者基于神经网络的近似能量性能预测模型[22-23],直接探寻过流部件几何参数的最优组合方式,该方法已逐渐成为离心泵水力性能优化设计的发展方向,同时也是众多学者研究的热点问题。

为此，以径向式导叶多级泵为研究对象,以过流部件关键几何参数为输入层,以研究对象的扬程和效率为输出层,构建反向传播(back propagation,BP)神经网络,并采用遗传算法(genetic algorithm,GA)优化BP神经网络的权值和阈值,建立径向式导叶多级泵水力性能预测模型,探索过流部件关键几何参数的最优组合方案,为进一步研究相似泵的水力性能优化设计方法奠定基础。

1 基于GA-BP神经网络的预测模型

1.1 过流部件关键几何参数

选择MD500-57型径向式导叶多级泵为研究对象,根据文献[24]发现影响径向式导叶多级泵水力性能的关键几何参数如表1所示。为后续径向式导叶多级泵水力性能优化设计方法的构建与求解,需要对过流部件关键几何参数的取值范围进行计算,即变量的约束。在对过流部件关键几何参数的取值范围进行计算时,取值范围不宜过大,否则将无法满足水力设计要求,同时取值范围不宜过小,否则有可能导致遗漏最优解。流体力学发展至今,随着速度系数法不断完善与改进,以及工程师和研究人员工程实践经验的不断丰富。因此将速度系数法和工程实践经验相结合,以研究对象的关键几何参数值作为基准值,建立了过流部件关键几何参数的取值范围,具体如表1所示。

1.2 BP神经网络

将BP神经网络应用于径向式导叶多级泵的水力性能预测中,首先将构建的试验样本归一化处理后作为BP神经网络输入层的输入信息,输入信息通过隐含层作用于输出层的神经元上,并产生输出信息；其后将BP神经网络产生的输出信息与实际结果的误差进行反向传播,将输出误差通过隐含层向输入层逐层反传,并将输出误差分摊给各层所有神经元,以此调整输入层神经元与隐含层神经元的联结强度和隐含层神经元与输出层神经元的联结强度,经过反复学习训练,确定与最小误差相对应的网格参数；然后将试验样本归一化处理后的其它数据依次输入BP神经网络内,重复上述调试与训练过程,直至准确地得到径向式导叶多级泵水力性能预测模型。

图1为具有代表性且常用的3层BP神经网络示意图,若输入层向量为A=(a1,a2,…,au,al)T,隐含层向量为B=(b1,b2,…,bγ,br)T,输出层向量为C=(c1,c2,…,cθ,ck)T,输入层到隐含层之间的权值矩阵用W表示,隐含层到输出层之间的权值矩阵用O表示,则各层中信息之间的数学关系如下。

(1)对于隐含层有

bγ=f(netγ)，γ=1, 2,…,r

(1)

(2)

式中：netγ为隐含层神经元bγ的输入值；ouγ为神经元aγ的权重；aγ为输入层第γ个神经元。

(2)对于输出层有

cθ=f(netθ)，θ=1, 2,…,k

(3)

(4)

式中：entθ为输出层神经元cθ的输入值；wγ为神经元bγ的权重；bγ为隐含层第γ个神经元。

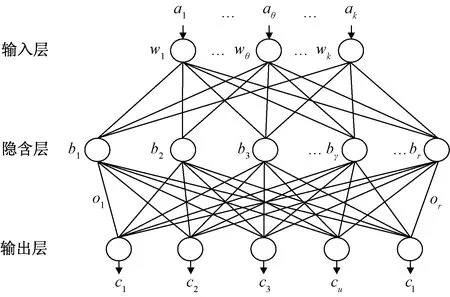
图1 BP神经网络结构Fig.1 Structure of BP neural network

1.3 建立GA-BP神经网络的预测模型

BP神经网络作为局部寻优算法,网络的初始权值与阈值是随机生成的,从而导致网络训练过程收敛速度较慢且易陷入局部极小值[25],无法获得最优解。而遗传算法是以概率选择为主要方法,依据“优胜劣汰”进化原理,以“网络误差最小”作为进化准则,在全局范围内搜索最优解[26]。因此将BP神经网络和GA算法相结合,以GA算法对BP神经网络的初始权值和阈值进行优化设计,能够显著提高网络收敛速度、预测能力和预测精度。

鉴于此,基于GA-BP神经网络的径向式导叶多级泵水力性能预测模型的具体优化流程如图2所示。

根据BP神经网络的构建流程,输入层和输出层的结构设计随训练样本的选择基本确定,即输入层的神经元为13个,即过流部件的13个关键几何参数,输出层的神经元为2个,即泵扬程和效率,而隐含层的神经元个数与激活函数的选择成为了BP神经网络结构设计中的核心问题。

针对隐含层的神经元个数,采用经验式(5)～式(7)计算得到隐含层神经元个数的上、下界值分别为6和13。为保证神经网络的精度,将取值范围扩大至6～15,在其他条件都保持相同的情况下,运用MATLAB软件仿真试验,不同隐含层神经元个数的训练误差与网络误差如表2所示。由表2可知,隐含层的神经元个数为10时,验证均方误差最小。因此选定隐含层神经元个数的最佳数目为10个。

(5)

图2 遗传算法与BP神经网络流程图Fig.2 Flow chart of GA-BP neural network

表2 隐含层神经元个数与相应的误差

(6)

l=log2n

(7)

式中：n为输入层神经元数量；l为隐含层神经元数量；m为输出层神经元数量；a为0～10的常数。针对激活函数的选定,以输入层的神经元为13个,隐含层的神经元为10个,输出层的神经元为2个,依次分别选取logsig函数和tansig函数作为BP神经网络各层的激活函数,采用相同的训练样本分别对网络进行训练,两种激活函数的误差结果如表3所示。由表3可知,采用tansig函数作为激活函数时,训练均方误差较小,因此选择tansig函数作为激活函数。

综上所述,所设计的BP神经网络具体参数如表4所示。

表3 两种激活函数对应的网络误差精度

表4 BP神经网络的具体参数选择与设计

2 预测模型的网络训练

2.1 基于正交试验方法的样本设计与求解

正交试验是试验设计中最常用的方法之一,其主要是利用正交表对试验参数进行组合试验方案设计,而正交表具有正交性、均衡分布性和综合可比性等特点,是一种高效的试验设计手段。鉴于此,采用正交试验设计方法对试验参数进行组合,构建试验参数的正交试验方案。

2.1.1 样本设计

试验参数共计13个,各试验参数采用3水平,进行正交试验方案的设计,共计54个试验设计方案,部分试验方案如表5所示。

2.1.2 样本求解

在正交试验设计方案的基础上,根据表5中各个试验设计方案中试验参数的不同组合方式,对研究对象的叶轮和径向式导叶的流体计算域进行重新建模,采用数值模拟计算54个试验设计方案所对应的扬程和效率,并将数值计算结果的扬程和效率作为优化目标数据,从而构建完整的正交试验设计的样本数据,具体如表6所示。

表5 部分正交试验的设计方案

表6 训练与测试样本

2.1.3 样本数据的归一化处理

根据样本数据归一化处理计算式(8),运用MATLAB软件对上述建立的正交试验样本数据进行归一化处理,归一化处理后部分结果如表7所示。

(8)

式(8)中：t′i为归一化处理之后对应的数值；ti为第i个数据的初始值；tmin为初始数值中的最小值；tmax为初始数值中的最大值。

2.2 预测模型的训练过程

2.2.1 选择训练函数

表7 样本数据的归一化处理

目前BP神经网络的网络训练法主要包括traingdm函数(动量梯度下降函数)、traingd函数(梯度下降反向传播算法)、traingda函数(自适应学习率的t函数下降反向传播算法)、traingdx函数(带动量梯度下降的自适应学习率的反向传播算法)和trainlm函数(L-M反向传播函数)等[27],依次采用上述训练函数对BP神经网络进行训练后,训练精度如表8所示。

由表8可知,采用trainlm训练函数对网络进行训练时,其模型精度为0.075,是所有训练函数中训练精度最高的。因此采用trainlm训练函数作为神经网络的训练函数。

2.2.2 网络训练参数设置

选择正交试验样本数据的前49组数据作为训练样本,选择初始种群数为60,交叉遗传的概率取0.65,设置变异概率为均匀变异,终止进化迭代步数为500步,同时设置BP神经网络的自适应学习速率为0.7,迭代步数为500步,目标误差为0.001。通过设置上述网络训练参数,径向式导叶多级泵水力性能预测模型的误差变化曲线如图3所示。

2.2.3 预测结果验证

选择正交试验样本数据的最后5组数据作为网络预测精度的验证样本,预测结果与数值计算结果如表9所示。

表8 训练算法及其对应的神经网络模型精度

图3 训练误差曲线Fig.3 Curve of network error

表9 检验样本预测结果与数值计算结果的比较

由表9可知,经神经网络预测的径向式导叶多级泵扬程最大误差为4.11%,效率最大误差为2.88%,预测精度误差均在5%范围以内,可满足后续基于GA-BP神经网络的径向式导叶多级泵水力性能优化设计,同时也基本可以满足工程应用的需求。

3 优化前后结果对比与验证

3.1 优化前后结果对比

MD500-57型径向式导叶多级泵过流部件的关键几何参数优化设计前后的对比结果如表10所示。

表10 关键几何参数优化设计前后的结果对比

3.2 优化前后试验验证

为了验证优化后径向式导叶多级泵的水力性能,所采用的试验平台为开式旋转水力机械试验台,其安装图如图4所示。

图4 优化后径向式导叶多级泵的试验安装Fig.4 Test installation of optimized radial diffuser multistage pump

图5为优化前后径向式导叶多级泵的水力性能曲线对比。由图5可以看出,优化后泵的扬程与效率均有所提高；从流量-扬程特性曲线来看,在0.75Q(Q为设计流量,500 m3/h)至1.0Q流量下优化后多级泵扬程增加较多,特别是在设计工况下多级泵扬程增加了2.4 m,而在其他流量下多级泵扬程增加不多；从流量-效率特性曲线来看,在0.75Q～1.0Q流量下优化后多级泵效率增加较多,该流量区间内多级泵效率平均提高了3.34%,同时径向式导叶多级泵的高效区范围变宽。表明优化后径向式导叶多级泵的水力性能有所提高。

图5分析优化前后径向式多级泵的流量-扬程和流量-效率特性曲线的变化情况,而多级泵的轴功率性能参数是径向式导叶多级泵水力节能优化的最直接体现。表11为优化前后多级泵的轴功率试验数据。由表11可知,当泵流量为507 m3/h时,多级泵的轴功率降低了1.58 kW。由此可见在设计工况附近,多级泵的轴功率明显下降。

通过对优化后径向式导叶多级泵的扬程、效率和轴功率等参数的对比分析可以发现,多级泵的性能得以提高与改善,同时也表明通过基于GA-BP神经网络的径向式导叶多级泵水力性能优化设计而获得的过流部件关键几何参数的组合是最优的,实现了径向式导叶多级泵的水力性能优化设计,由此也证明了提出的径向式导叶多级泵水力性能优化设计方法的可行性与科学性。