多足机器人的设计与仿真分析

翁杰弟，许锦昌，何伟锋，刘烁超，李湘勤

（韶关学院智能工程学院，广东韶关 512000）

0 引言

仿生多足机器人的设计灵感来源于自然界的多足爬行动物，例如猎豹、狗和壁虎等，对其进行机构模仿设计[1]。仿生多足机器人的主要特点是只需要断续、离散的着地点，既能在坚硬平地上行走，也能跨·越沟壑和障碍物，具有广泛的地形适应性[2]。多足机器人往往可以在地形复杂、环境恶劣的救灾、煤矿、农业和军事等领域中，发挥较好的作用并完成任务[3]。因而多足机器人在这些领域中都有较好的应用前景和较高的研究价值及意义。

足式步行机器人的研究已成为现代科学研究的热点之一。国外研究成果中最具有代表性的是美国波士顿动力公司2008年研制的“big dog”[4]和2013年研制的“猎豹”。国内也取得了一定的成果，如哈尔滨工业大学开发的两栖仿生机械蟹[5]，南京航空航天大学开发的仿壁虎爬行机器人[6]和山东大学开发的由液压驱动的多足机器人“SCalf-1”[7]。

在农业生产活动中，常存在柔软地面或泥泞作业环境，本文以一种可适用于凹凸不平、柔软及泥泞地面行走的多足机器人为研究对象，进行建模仿真和运动轨迹优化。利用三维建模软件SolidWorks设计出仿生多足机器人，利用运动学分析软件ADAMS对其机构设计的合理性、行走能力、爬坡能力和越障能力等性能进行仿真分析，以验证该多足机器人具备在复杂地农业生产作业环境中的行走能力。

1 多足机器人的建模设计和运动学分析

1.1 多足机器人的建模设计

基于六杆牵引机行走机构设计的多足机器人简化三维模型如图1所示。该机器人的总体尺寸为长900 mm，宽600 mm，高450 mm。为了使虚拟样机运动仿真结果与物理样机实际运动结果相似，适当的调整加大前座和后座的质量以充当需要补充的质量块，使多足机器人模型整体质量达接近物理样机的质量。

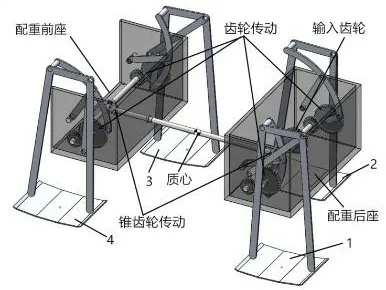
图1 多足机器人在SolidWorks中的整体模型

1.2 多足机器人的运动步态规划

对步履机器的四条腿进行编号，便于运动学分析。通过模拟四足动物的步态运动以实现较好的步态运动，将该多足机器人的前部和后部通过锥齿轮来实现前座和后座的连接传动，以实现1足和3足同步，2足和4足同步，通过改变左部和右部曲柄初始位置的相位差来调节步态。左部和右部的连接传动通过输入电机到齿轮，再传动到以曲轴为形式的曲柄上，避免杆件之间的干涉，从而实现连续腿部基本机构的迈步功能。

如图2所示为该多足机器人的运动步态，其中○足表示该足处于离地运动状态，“●”足表示该足处于着地运动状态。图2a为多足机器人的运动准备阶段，图2b到图2e为一个步态周期。图2b中1足和3足同步迈出，图2c中1足和3足作为支撑并使多足机器人躯体向前移动，图2d中2足和4足同步迈出，图2e中2足和4足作为支撑并使多足机器人躯体向前移动得到图2f的下一个步态周期的初始状态。

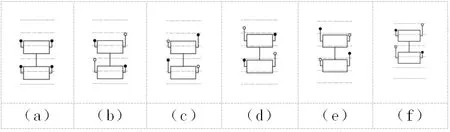
图2 多足机器人运动步态

1.3 多足机器人的运动学分析

已知多足机器人腿部基本机构的足部坐标，通过运动学正解求出多足机器人的躯体质心的位姿。在多足机器人躯体质心处建立坐标系{C}，设该坐标系在机器人运动初始位置时与大地坐标系{G}重合，当质心坐标系{C}相对于大地坐标系{G}的X、Y、Z轴分别移动了XC、YC、ZC，绕X、Y、Z轴分别旋转角度时，可以得出质心坐标系{C}相对于大地坐标系{G}的位姿变换矩阵为[8-9]：

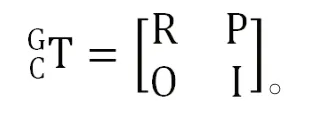
2 多足机器人的仿真分析

对上述的多足机器人利用虚拟样机技术在斜坡和复杂地面环境中的运动状况进行仿真分析。将已经装配好的多足机器人简化模型导入在ADAMS中，并对各铰链添加转动副，对齿轮和锥齿轮添加齿轮副，需相对固定的构件添加固定副。约束副的添加要注意对象的选取，位置的确定，方向的定义，特别应注意在齿轮副中的共速点（Common Velocity Marker）的制作和该点Z轴应与齿轮切向速度方向平行。

设定地面材料为混凝土，足部硬橡胶和干混凝土的静摩擦系数为0.9和动摩擦系数为0.7[10]。通过在四只足上添加与地面的接触力，定义静摩擦系数和动摩擦系数。在输入齿轮上添加240°/s的电机，设定仿真时间为24 s，step为200进行仿真。

2.1 通过斜坡地面运动分析

利用斜坡地面来具体分析该多足机器人的爬坡能力，并从中得到其爬坡角度适用范围。在建立斜坡模型，添加前述相同的接触力参数、静摩擦系数和动摩擦系数，建立多足机器人通过斜坡地面的仿真模型。设定仿真时间24 s，step为200，分别多足机器人在坡角为5°、10°、25°、45°、65°五种坡面的通过能力进行仿真，速度及加速变化规律如图3、4所示。

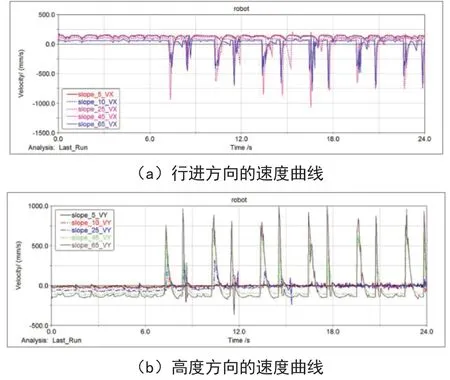
图3 在所选坡度的斜坡运动时多足机器人质心的速度曲线

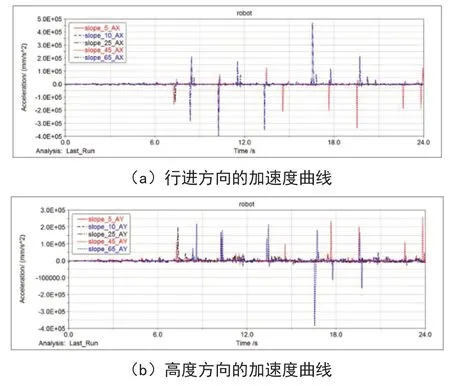
图4 在所选坡度的斜坡运动时多足机器人质心的加速度曲线

多足机器人在0～7.56 s内在平地上运动，在7.56～24 s内在斜坡上运动。多足机器人质心在行进方向上的位移随着仿真所选坡度的增大而逐渐变缓。当坡度达到25°时，多足机器人上坡出现困难，发生了一定的滑移；当坡度达到45°时，在7.56～24 s内，多足机器人在行进方向上的位移在630～801 mm的范围内上下波动，发生了较大的滑移，已无法继续上行。这种滑移是由于机器人足部与斜坡之间的摩擦力不足以抵消其自身的重力在沿着斜坡的行进方向反方向所产生的阻抗力，这种滑移程度随着斜坡坡度的增大而增大。根据图3、4结果显示，当多足机器人所趴坡度在25°以下时，多足机器人质心在行进方向上速度和加速度随着坡度增大而减小，且速度和加速度波动不大，较为平稳；当坡度达到25°以上时，多足机器人速度和加速度同样随坡度增大而减小，但出现了较大的速度和加速度突变。分析可知，该多足机器人在坡度为25°以下的斜坡上运行时，在行进方向和高度方向上运动较为平稳，有一定的爬坡能力；当多足机器人在坡度达到25°以上的斜坡上运动时，出现了较大的位移波动及速度和加速度突变。

2.2 通过复杂地面运动分析

考虑到农业生产作业环境中存在一些凹凸不平、斜坡面等现象，需要确定多足机人在复杂地面行走的性能。该多足机器人的腿部基本机构的单步跨距为315.65 mm，单步的幅度为60.59 mm，由3.1得到其爬坡的最佳范围在25°及其以下，所以现设计一种能使该多足机器人通过的复杂地面。以峰-峰值为56 mm，周期为785 mm的正弦曲线。并倾斜12°作为此次仿真分析的复杂地面。多足机器人通过复杂地面的模型如图5所示。同样以前述接触力参数、静摩擦系数和动摩擦系数应用到本次仿真中，设定仿真时间24 s，step为200进行仿真。将这次仿真所得位移曲线与通过坡度为12°的斜坡时所得位移曲线进行对比得到如图6所示的多足机器人的质心位移对比曲线。多足机器人通过复杂地面时质心速度曲线和加速度曲线如图7、8。

图5 多足机器人通过复杂地面的模

图6 复杂地面和通过12°斜坡时行进方向上的位移对比曲线

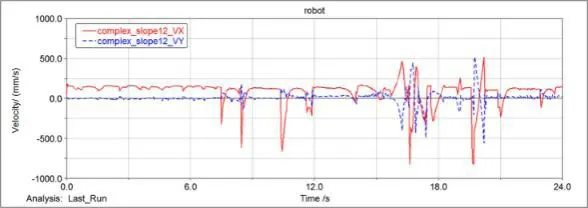
图7 通过复杂地面时质心速度曲线

图8 通过复杂地面时质心加速度曲线

如图6所示，多足机器人在7.56 s时开始登上复杂地面，并在剩下的16.44 s内越过了以两个特定的正弦函数曲线周期。多足机器人在通过复杂地面时比通过12°斜坡时的主运动行进方向的位移较小，有一定的位移波动。结合图7中的多足机器人通过复杂地面时在行进方向的速度总体上平稳，但在8.45 s、10.44 s、16.60 s和19.68 s处出现了较大负向速度突变，使得多足机器人出现了短暂的后退。再由图8中的多足机器人通过复杂地面时在行进方向的加速度在17.4 s和19.72 s处达到了54 261.67 mm/s2和71 231.42 mm/s2，但总体加速度波动不大。

综上所述可以得到在通过复杂地面时该多足机器人在行进方向上位移、速度和加速度波动不大，总体上仍然是呈现稳步上升趋势；在高度向上有较大的位移、速度和加速度波动，这是由于该特定的正弦函数从波谷到波峰之间的拐点处的坡度达到了35.4°，已超过了该多足机器人爬坡的最佳坡度范围。由以上分析可以得出该多足机器人能过通过设定的复杂地面，具有一定的越障能力和较好的地形适应性。

3 结语

通过利用虚拟样机技术对腿部基本步行机构和四足仿生机器人进行仿真分析，能够简化理论计算，减少制作物理样机的成本和时间，增加实验数据的可靠性。本文研究的多足机器人由于具有较大的触地滑板，可以在柔软或泥泞地面上对自身提供良好的支撑效果，通过仿真分析，验证该多足机器人具备25°以下的爬坡能力，在凹凸不平的复杂地形下能较为稳定的行走。验证了此种多足仿生机器人可针对性适用于农业生产中的泥泞或凹凸不平地面的行走作业。