动车组牵引变流器支撑电容全寿命周期可靠性研究

李夺

（中车青岛四方机车车辆股份有限公司 山东省青岛市 266000）

直流支撑电容作为动车组牵引变流器设计和应用的关键元件，主要起到缓冲交流侧和直流侧间的电能转换，平稳中间直流电压，储能并提供瞬态能量转移的作用[1]。在支撑电容运行服役的过程中，在自身因素和外界因素的共同作用下，存在损坏失效的风险，可能发生电气击穿导致电容短路引起爆炸，给动车组的正常工作造成了严重的安全隐患[2]。而且，动车组上牵引变流器和辅助电源的支撑电容完全是壳体密闭式，内部电气绝缘结构复杂，若对电容经常拆卸检查将造成很大的人工和时间成本。

因此，针对正在运行服役的支撑电容，为了确保动车组运行可靠性，同时降低检修成本，需要开展的牵引变流器和辅助电源支撑电容可靠性研究具有重要的理论意义和工程价值。

1 研究方法

支撑电容在运行过程中，由于电应力与热效应的作用逐渐老化，但由于金属薄膜电容器的自愈特性，其性能在长时间范围内能保存稳定运行，在自愈范围内，其容值变化较为缓慢，仅以容值的变化情况无法准确评估电容的可靠性，结合试验结果，发现介质损耗、局部放电量以及电容容值能够较好地表征电容性能随里程的变化规律，另外，耐久性试验过程中容值随时间衰减与实际运行里程具有较好的对应性，因此基于以上物理量对支撑电容可靠性进行评估，评估流程如图1所示。

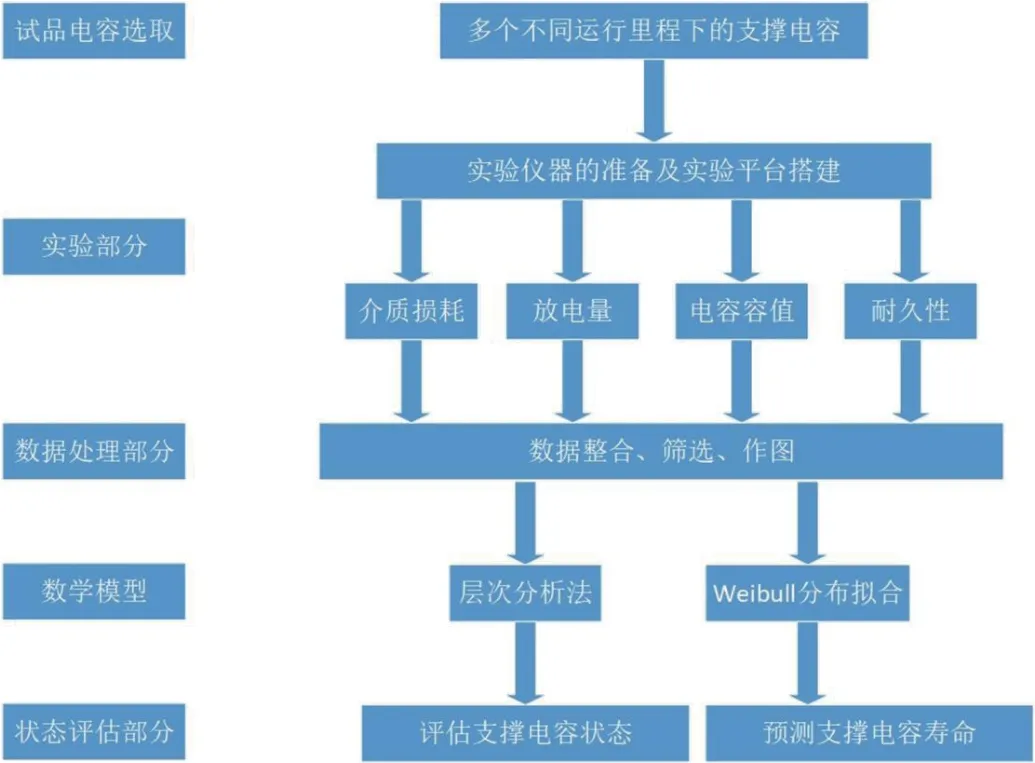
图1：动车组牵引变流器支撑电容可靠性评估方法及流程图

2 主要关键技术研究

层次分析法（Analytic Hierarchy Process）是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法，是一种定性与定量相结合的系统分析方法[3]。该方法的原理是将复杂问题降级化，分解成小指标，在所有指标间进行对比分析，得到多种解决问题的办法，由于各个方案所占权重不同，通过分析最后得到最好的问题解决办法[4]。

表4：特征值和特征向量

2.1 依据指标结构，建立层次模型

首先，根据所要探究的具体问题，选出问题的各项评价指标，评价指标涉及了所评价目标的全方面信息，指标涉及出不同层次、不同维，可分为多个层级。

2.2 依据指标划分，构造判断矩阵

利用托马斯·塞蒂的“1-9 标度法”进行指标层级构建[5]，根据指标层次模型，对每一层中的每个指标进行比较，比较后可确定出相对重要的指标层次详见表1。

表1：指标层次表

依据上表，构造的成对比较矩阵如下：

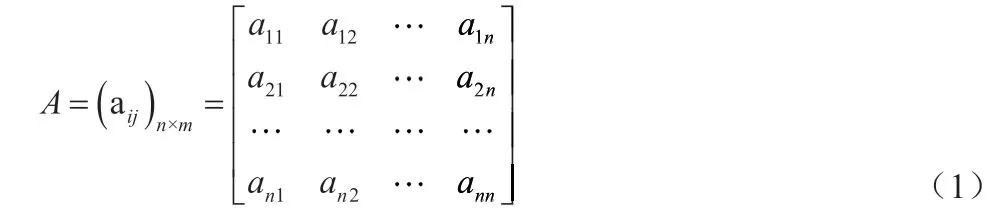
其中，用aij表示第i 个因素相对于第J 个因素的比较结果。

通过上述定义可以得知，成对比较矩阵(aij)n×m，满足下列性质：

(aij)n×m也称为正互反阵。

2.3 计算权重

组建好判断矩阵之后，对构造的矩阵实行层次单排序和判断矩阵一次性检验，求解判断矩阵（标记为A）的最大特征根问题：

2.4 检测一致性

检测一致性一共分为3 个步骤。

（1）一致性指标 CI。

注 2.3 以上定理和命题给我们提供了2个是完备空间但不是紧空间的例子。更重要的是,借助定理2.3—2.6,可以确定以下度量空间的完备性。

其中，n 的值为所选因素的个数。

（2）查找相应的一致性指标 RI 所对应的不同矩阵阶数，见表2。

表2：平均随机一致性指标 RI 标准值

通过表2所示，对于1、2 阶判断矩阵都完全具有一致性。当阶数超过2 时，判断矩阵的一致性指标CI 和同阶平均随机一致性指标RI 之比，用检验系数CR 表示随机一致性比率。

（3）计算检验系数 CR。

利用层次分析法检验判断矩阵是否具有一致性是在计算CR 的值，也就是随机一致性比率的值中实现的，表达式如下：

当 CR=0 时，说明矩阵一致性极佳，可以通过检验。

当 CR<0.1 时，说明矩阵一致性一般，但是可以通过检验。

当 CR ≥0.1 时，说明矩阵的一致性很差，则需要对举证的元素取值进行调整应对，直到 CR<0.1 才能使判断矩阵具有满意一致性。

3 试验结果分析

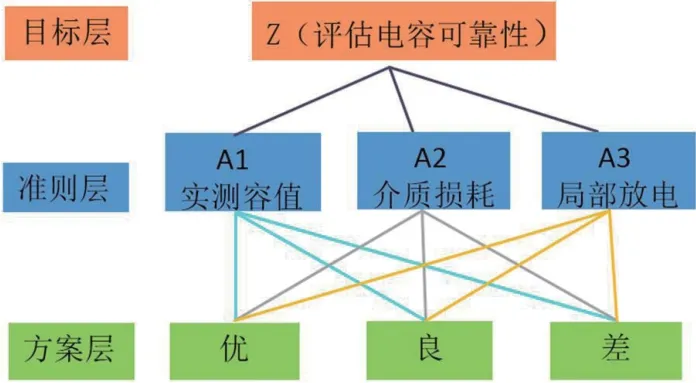
图2：牵引变流器支撑电容可靠性评估模型

3.1 构造成对比较矩阵

对于各个因素间重要性的比较，采取计算数据变化率的方法来定量判断，即：针对某一里程电容，计算它的实测数据与该电容的出厂初值的变化率，变化率大的因素则相对重要一些。

在电容评估问题中第二层A 的各个因素对目标层Z 的影响两两比较的结果如表3。

表3：准则层判断矩阵

得到成对比较矩阵A 如下：

3.2 计算权向量并给出一致性检验

3.3 确定方案层分数

牵引变流器逆变电容方案层分数打分如表5、表6。

表5：牵引变流器油式电容方案层分数

表6：牵引变流器干式电容方案层分数

3.4 计算最终得分评估电容

最后得分Z。

如600 万公里的牵引变流器逆变电容数据如下：耐久性前后容值衰减5.5%，电容值测试值为1255.62μF，平均局部放电量为330pC，将其计为向量形式如下。

通过方案层分数表可知，耐久性前后容值衰减为差，得分1 分；电容值测试值测试为优，得分3 分；平均放电量测试为差，得分1 分。通过加权求总得分为。

即1

其余电容状态根据方案层分数统计，查阅附录D 层次分析法真值表，确定部分结果如表7所示，完整评估结果如附录E所示。

表7：层次分析法评估结果

4 结论

本文就动车组支撑电容寿命周期可靠性评估提出了有效的评估方法和评估流程，通过分析得出，240 万里程的电容服役性能较优，其性能随里程的变化不明显；480 万里程牵引变流器逆变电容服役性能有所下降，状态良好；600 万公里牵引变流器电容，容值、介损、耐压、浪涌放电变化明显，状态较差，建议采取相应检修措施。