基于遗传算法的中小城市地铁运营与建设的方案
2021-03-07吴家扬刘雯景
吴家扬 刘雯景
(广东海洋大学 广东省湛江市 524088)
1 引言
在经济高速发展的当下,作为城市动脉的地铁,给人们带来交通便利、快捷,一种千里江陵一日还的幸福生活。但中小城市地铁建设成本昂贵、出行亏损、早晚高峰期交通拥堵,运用合理科学的运营和优化建设设计刻不容缓。根据相关报道显示呼和浩特地铁2019年年底开始试运营,目前已有地铁1 号线和2 号线两条正在运营的线路。然而,因线路数量、人口基数相对较少和站点选址上的问题地铁运营收入依然较低,从而引进科学的运营方案设计来有效降低运营成本提高运行效率势在必行。通过实例对基于遗传算法与确定性模型的公交调度结果进行比对,结果表明,基于遗传算法获得的地铁调度模糊最优解比确定性模型更为合理。[1]
2 问题分析
2.1 基于遗传算法模型分析
首先对原发车方案进行评价,其次是求最优发车的间隔时间和最优的车厢数。车箱数默认为6,把站点人数分成平峰期和高峰期,采用均值化进行处理,再利用遗传算法求发车最优间隔时间。利用所求的最优时间和成本函数,去比较车厢数不同时的利润值。当利润值最大时,就为最优的车厢数量。
3 模型的建立与求解
3.1 基于遗传算法模型分析
3.1.1 数据的预处理
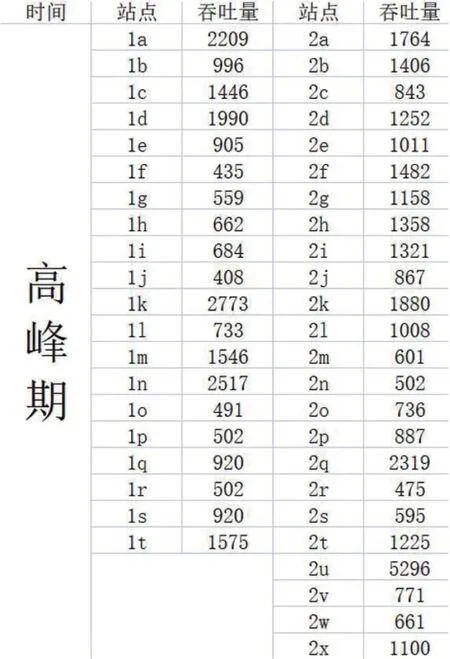
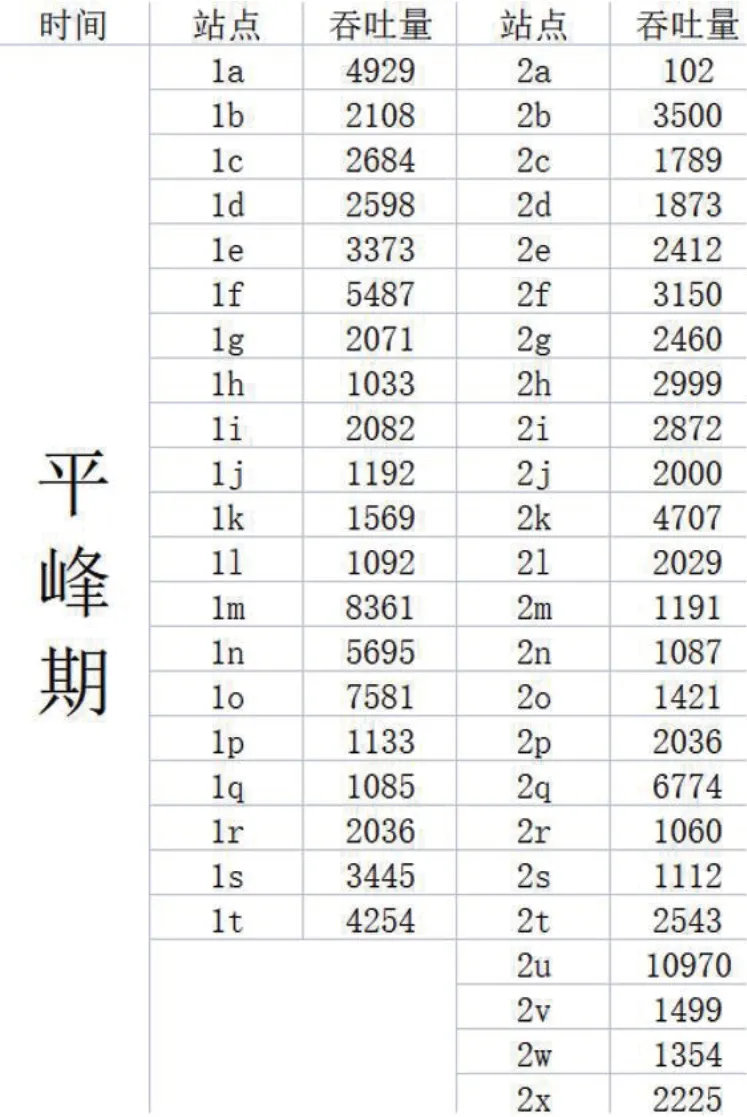
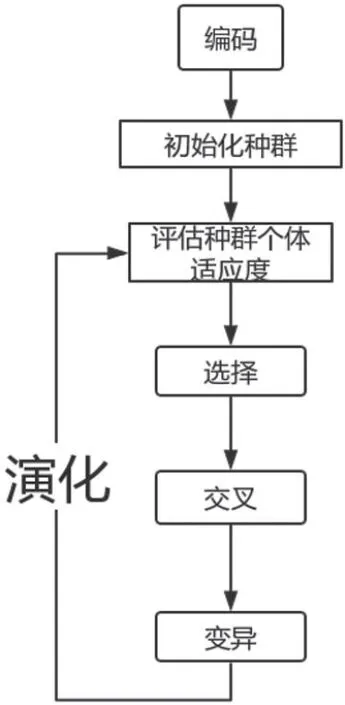
我们采用的数据是呼和浩特市2020年9月1日至2020年9月14日,2 条线路,45 个站点,间隔为15 分钟的客流数据。将地铁的运营时间分成高峰期和平峰期,早高峰为7:00-9:00,晚高峰为17:00-19:00,其余时间为平峰期。我们把早高峰期和晚高峰期的时间用S1去表示,平峰期的时间用S2去表示。我们用fijkq去表示第天,第j 号线,第k 个站点的人数,q 表示的是运营时间的分类。其中(0 fijkq这个变量将被用于计算目标函数的最优值。为了优化后面求最优值的过程,首先对S1和S2两个时期14 天的数据作均值化处理,用去表示每个站点14 天的平均值,q 的取值为0 和1,即 通过上面的统计我们可以得到S1和S2两个时期每个站点的吞吐量信息,如图1、图2所示。 图1:高峰期的客流情况 图2:平峰期的客流情况 3.1.2 构建遗传算法模型 我们在求解发车的时间间隔t 用的是遗传算法,该算法的实现如表1所示[2]。 表1:算法步骤 步骤1.确定优化方程 该问题的关键是设置一个合理的间隔时间,从而找到盈利最优的模式。可以把该问题看成是如何求最小成本,也就是就能够最大化盈利。查阅资料[3],我们考虑如下公式,其中用α 表示列车运营成本权重系数,用β 表示乘客出行成本权重系数,C0表示轨道交通系统乘客出行成本,Cv为轨道交通系统列车运营成本。成本函数可表示为: C=αC0+βCv 运营时间分成高峰期和平峰期,早高峰为7:00-9:00,晚高峰为17:00-19:00,其余时间为平峰期。依据这两个时间段,采用熵权法去确立权值,高峰期用α1去表示,平峰期用α2去表示。最终,最优的发车间隔通过t=α1×t1+α2×t2。 步骤2.生成初始解编码 表4:早高峰期方案设计 表5:晚高峰期方案设计 选择的编码方式是二进制编码,将十进制的数字转换成二进制。由于方程中xi的范围处于[0,128]之间,因此统一转换为7 位的二进制数,例如当xi=8 的时候需要转换成xi=00000100。我们生成的初始解有4 个,分别是4,6,8,10,它们经过编码得到的结果,分别是: x1=00000100 x2=00000110 x3=00001000 x4=00001100 步骤3.评估种群适应度,淘汰最小解。 把上述生成的变量分别代入目标函数中,通过Max(xi)去比较4 个解的概率,得到概率最小的解为xk,概率最小的解要被概率最高的解替换。即: xk=Max(xi) 步骤4.交叉,变异。 是否进行变异需要用过概率去决定。其中默认变异率为Pm=0.001,变异概率P=Pm×m×q 可以通过求取。其中是编码的位数用m 去表示,解的群体数用q 去表示。将求得的P 于1 进行比较,当P<1 不进行变异,当P>1 进行变异。对初始解进行交叉,交叉操作如图3所示,即对 位二进制数的后四位进行交叉变换。 图3:交叉变换的示意图 步骤5.解码得到最优值。利用函数BinToDec()进行解码转换 在前面求解的最优发车间隔t 的时候,我们已经建立了关于成本函数,当成本函数值越小,地铁公司的盈利越高。在求解最优车厢数的时候,需要通过比较车厢数n 为3,4,5,6,7,8 时候的日成本量,当日成本最小时,即为车厢数n 的最优值。其中最优发车间隔默认为t=6,将上述所说的n 与t 代入函数中计算比较,即可求得最优发车间隔、最优车厢数。 3.1.3 模型参数的设置 在求解的时候,我们在遗传算法的参数设置[5],如表2所示。 表2:参数设置 3.1.4 模型结果分析 通过图4所示的流程,最终我们在迭代次数为75,求出了平峰期的最佳间隔时间为t1=8.3,高峰期发车间隔5.4。损失函数如图5所示。 图4:遗传算法流程 图5:损失函数图像 利用熵权法我们可以求得的权重平峰期α1为0.3,高峰期α2为0.7。得到结果如表3所示。当车厢数为4 时,求得的成本节约18%。 表3:计算结果 3.2.1 错峰出行目标函数的建立 以最大客流量站点为2c 为研究对象,比较不同的错峰出行方式会对该站点的客流量造成影响。 了解到该地区的学生群体的上学时间7:45-8:00 之间,放学时间17:00-18:00。上班群体的时间为7:30-8:10 之间,下班时间为17:30-18:15。可以看见现在的上学时间和上班群体的时间存在较大的交叉性。 因此我们根据实际情况,对早高峰期和晚高峰期分别设置了3种不同的方案[6],在不影响上班群体和学生群体的出行情况下,尽可能的减少出行时间的交叉,如表格4、5所示。 考虑到学生群体有到校时间的准则,上班群体也有到岗时间的准则,因此它们在不同时间段将会有不同的权重。用αi1去表示用第i 个方案上学时间的权重,用αi2去表示用第i 个方案上班时间的权重。 3.2.2 错峰出行目标函数的求解 舒适度的结果如表6、表7所示。从表中可以看见,早高峰期与晚高峰期都是方案三的拥挤度最低,因此上学时间设置为7:20-7:30,上班时间为8:35-8:55,放学时间为16:50-17:20,下班时间为17:40-18:15,能够有效减少2c 站点所出现的拥挤情况。 表6:早高峰期舒适度 表7:晚高峰期舒适度 综上早晚高峰期的优化计算,可实现最终平峰目标的方案设置,如表8所示。 表8:平峰目标方案 在地铁1 号线,2 号线各站点人流量均互不影响的前提下,会忽略实际生活中出现的换乘等情况,且统计样本有重复性。地铁运营成本统计忽略实际能耗成本,维护成本等方面,与实际会有较大出入。 模型逻辑清晰,可操作性强,可移植性强。模型基于数学推导,分析严谨,稳定性高,结论具有普遍意义。结合实际城市地形分析,结论严谨,有一定程度上的实用价值。 在选址问题上只选取了一天的站点吞吐量分析,而具体人流量会受交通管制,天气,节假日等因素影响。模型忽略了具体城市的原有交通布局方案,实际合理性上会有一定程度欠妥。 本文使用的模型移植性高,如遗传算法可用在各类优化问题上求解,基于遗传算法改进的站点优化模型可应用在公共基础设施选址等具有实际效益的问题上。[7]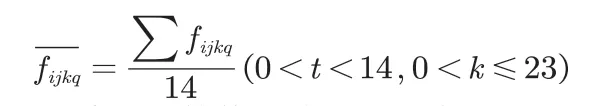







3.2 以2c站点为例提出错峰出行建议




4 模型的评价及优化
4.1 误差分析
4.2 模型的优点
4.3 模型的缺点
4.4 模型的推广
