导管架平台上部组块双船拆除
2021-03-06李健行付振秋AndyWANG
李健行,李 欣,付振秋,孙 浩,Andy WANG
(1. 上海交通大学 海洋工程国家重点实验室,上海 200240;2. 上海交通大学 三亚崖州湾深海科技研究院,海南 三亚 572024; 3. DNV Oil and Gas,上海 200336)
0 引 言
21世纪初期,全球有超过7 000个海洋油气生产设施,一般海洋油气设施的设计寿命约为20 a,随着其服役时间的延长,有相当一部分设施都将面临达到服役寿命的问题。按照相关法律要求,这些达到服役寿命或不再使用的设施必须进行妥当的退役废弃处理。自从1973年以来,海洋平台拆除数目逐年增多,2006后,每年的拆除数目都在百座以上,目前全世界已经陆续拆除超过5 000座平台。根据我国相关统计信息,我国会有近100座海洋平台陆续进入弃置阶段,预计今后几年会有十多座平台将被拆除,并且其中大多数为导管架平台,拆除方案各有不同[1-3]。据国外拆除费用统计,在北海地区,拆除总成本约占设备初投资费用的3%~7%,且部分平台的导管架拆除费用高于建造成本。因此,废弃海洋平台的拆除工作将催生一个产业,成为海洋工程界的一个新的经济增长点。导管架作为废弃桩基平台的重要组成部分,结构复杂,在服役期间,腐蚀等原因会使结构受到大幅削弱和破坏[4],重心位置会发生变化,增大了拆除风险。同时,导管架的拆除涉及技术领域较多,拆除作业周期长、难度大,而且对海洋环境有潜在的污染风险,一旦发生事故,将造成巨大的损失[5]。
目前国外对于海洋废弃平台拆除的问题已经有所研究,但是国内对于这个问题的研究仍在起步阶段。双驳船浮托安装是平台服役时由两侧驳船使用浮托方法将其安装至施工区域,而双浮拖组块拆除则是其逆过程。其中涉及的较多问题不能简单地进行逆向考虑就可解决[6-7],其中的安全性和各种水动力问题仍然需进行细致的研究。
本试验采用完全模拟实际施工过程的方法,模拟进船、质量转移、退船、满载行驶等4个过程。其中质量转移阶段是双驳船对导管架平台进行抬升,平台的质量逐渐转移至双驳船但导管架平台尚未产生位移的阶段。通过固定导管架平台模型,调整双驳船压载,完成模拟导管架平台质量转移0、50%、100%等3个工况的波浪试验。将导管架平台模型通过甲板耦合装置(Deck Mating Unit, DMU)与桩腿支撑装置(Leg Supporting Unit, LSU)连接在双驳船之上,并结合DP系统,进行双驳船托举平台满载行驶试验。之后进行双驳船与第3条运输驳船的进船、退船的配合试验。着重进行上部组块质量转移完成阶段的时域模拟,并与试验数据进行相应对比,以此对实际施工阶段的安全性进行指导。双浮托法拆除上部组块示例如图1所示。
1 计算理论
1.1 坐标系定义
根据右手法则,选择全局坐标系O-xyz,其原点为DP设定点,x轴指向北,y轴指向东,z轴(未使用)指向下方。船在xy平面上的方向定义为顺时针旋转,船首指向北方的方向为零参考点。

图1 双浮托法拆除上部组块示例
驳船的速度以船体坐标系作为参考,速度矢量v由分量u、v、r组成,描述朝船首方向、向右舷侧向和顺时针旋转方向的速度,θ为船首方向与x轴的偏角,CoG为船体坐标系原点,坐标系如图2所示。

图2 坐标系示例
1.2 频域计算理论
假设流体为理想流体,在满载工况下,2条驳船为无航速的2个浮体M与L,其中一条驳船的速度势φ公式为

(1)
式中:φI为入射势;φl,M为作用于驳船M的入射波速度势;φD,M为另一条驳船L对驳船M产生的绕射势,包括驳船M对自身产生的绕射势;φj为当浮体M没有产生运动时,由于另一条驳船的振荡而作用于驳船M上的辐射势,包括驳船M对自身产生的辐射势;ξj为驳船自由度j的运动响应,j=1~6为驳船M在6个自由度上的运动(纵荡、横荡、垂荡、横摇、纵摇和艏摇),j=7~12为驳船L在6个自由度上的运动响应;ω为波浪频率;t为时间。
把入射势展开,公式为

(2)

代入拉普拉斯方程进行求解:
2φ=0
(3)
边界条件如下。
统一自由面条件:
(4)
平整海床条件:

(5)
式中:n为垂直于物体表面与流场正方向相同的单位向量。
物面条件:
(6)
远方辐射条件:
(7)
通过格林公式将式(3)转化为物面上的积分方程进行求解,公式为
(8)
式中:Sb为驳船的湿表面。
对驳船湿表面绘制网格,可以进一步得到:
(9)
式中:i=1,2,3,…,N为网格数量;Sk为第k个网格的面积。
最后获得驳船频域的运动方程为
(10)
式中:mij、Cij、Fi分别为驳船的质量矩阵、静恢复力矩阵和所受波浪力;Aij为附加质量矩阵;Bij为阻尼矩阵;ξj为驳船6个自由度的运动。
1.3 时域运动方程
基于施工条件,考虑一阶波浪力,风、流力,推进器推进力,横向护舷力,DMU、LSU作用力构建多浮体动力学方程:
(11)

可参考Newmark逐步积分方法[8]进行求解。
2 质量转移阶段的数值模拟分析
由于导管架平台的重心不确定性且某些结构腐蚀导致施工难度加大,因此进行浮托操作时将导管架平台的质量转移到双驳船之上的质量转移阶段是施工时面临的主要危险阶段。由于双浮体之间有相互作用,因此在波浪中受到的波浪力和辐射力会存在耦合作用和相互干扰[9-10],也更为复杂。并且当质量转移完成时,原本导管架平台的所有约束都将失去作用,一旦发生危险会带来不可挽回的严重后果。因此有必要对于这一阶段各个关键组成部分的性能进行进一步的分析研究。
使用DNV Sesam中的Sima模块进行多浮体耦合运动时域分析,使用其搭载的的Simo求解器模拟海洋工程作业。对质量转移完成阶段进行数值模拟分析,计算双驳船系统的水动力参数和DMU受力大小,并给予不同有义波高与方向的波浪载荷,观察总体水动力性能是否在合理范围内。
2.1 船体主要参数和建模
使用中远航运股份有限公司现有的姊妹船泰安口与康盛口自航式半潜驳船,2艘船载重量均为18 000 t,均由广船国际股份有限公司建造完成。其中,泰安口船具有特殊的船体(没有船墙)结构,并且装置多个目前国际领先和个性的自动控制系统设备。2艘驳船外形如图3和图4所示。

图3 泰安口

图4 康盛口
试验模型采用的缩尺比为37,由于双船系统存在耦合,2艘驳船中间的波面会有一定程度的升高[11],在HydroD中可以对驳船之间的附连水采用单独绘制网格的方式,较好地模拟这一现象。2艘驳船和上部组块的主要参数如表1和表2所示。
经过处理后,参与时域水动力计算的模型如图5所示。
2.2 海洋环境条件
为保证控制系统的精确性和施工的安全性,有效波高小于1.5 m且风速不大于1.60 m/s是施工对环境的基本要求。欧洲北海海域海况恶劣,尤其是秋冬季节会有有效波高超过7 m的大波高频发生。但是夏季因为不同纬度温差小,西风风力较小,在这个窗口期环境条件较为理想。选取JONSWAP波谱,Gamma值为3.3,平均风速为1.35 m/s,有义波高Hs为0.75 m进行数值模拟和模型试验,其他条件如表3所示。

表1 运输驳船主要参数

表2 运输驳船上部组块主要参数
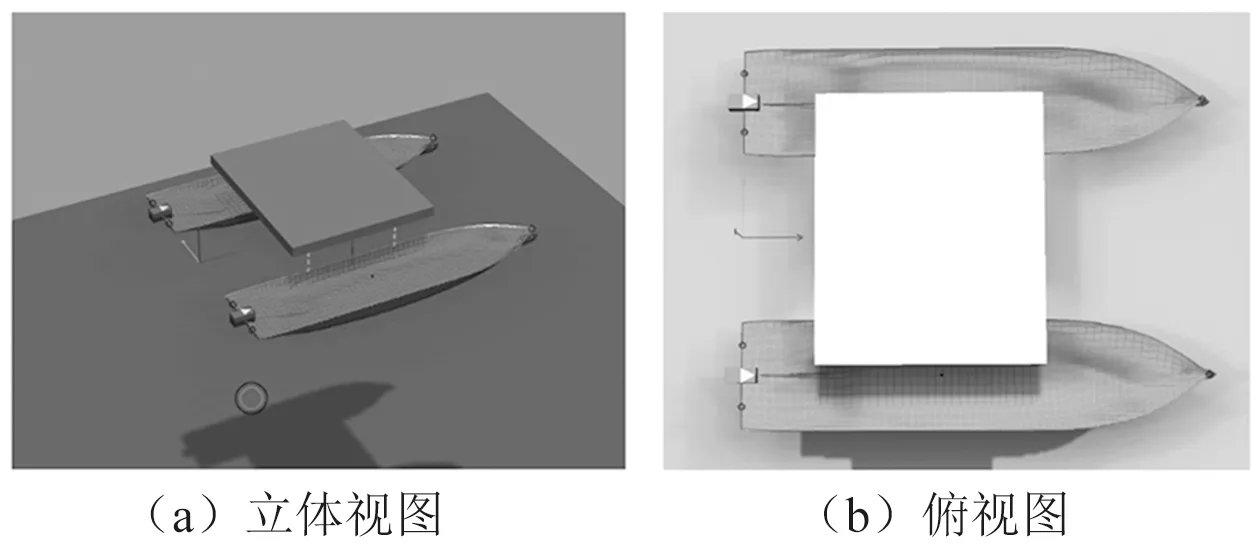
图5 Sima水动力模型
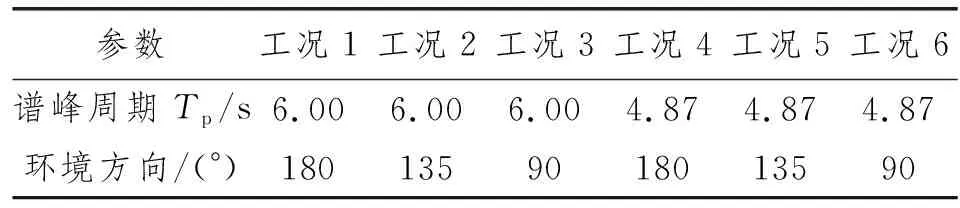
表3 海洋环境条件数值
生成的波浪频谱如图6所示。

图6 波浪能量密度频谱
2.3 驳船网格模型
对于2艘驳船,在Genier中建模并生成网格,之后导入HydroD中生成Wadam水动力模型。为了表述方便,在试验与计算中把2艘双浮拖船命名为k-class 1和k-class 2,其网格如图7所示。

图7 k-class网格模型
2.4 时域模拟结果
通过时域计算获得平台上部组块质量转移为0、50%、100%等3个阶段的驳船运动情况,并分别提取平均值与幅值。调整驳船间距进行计算发现,在DMU横向和纵向约束最大尺寸的10%范围内进行运动不会对驳船与上部组块的配合造成危险。因此,选取水平运动为0.2 m、竖直运动为0.35 m作为安全临界值,结果如表4所示。
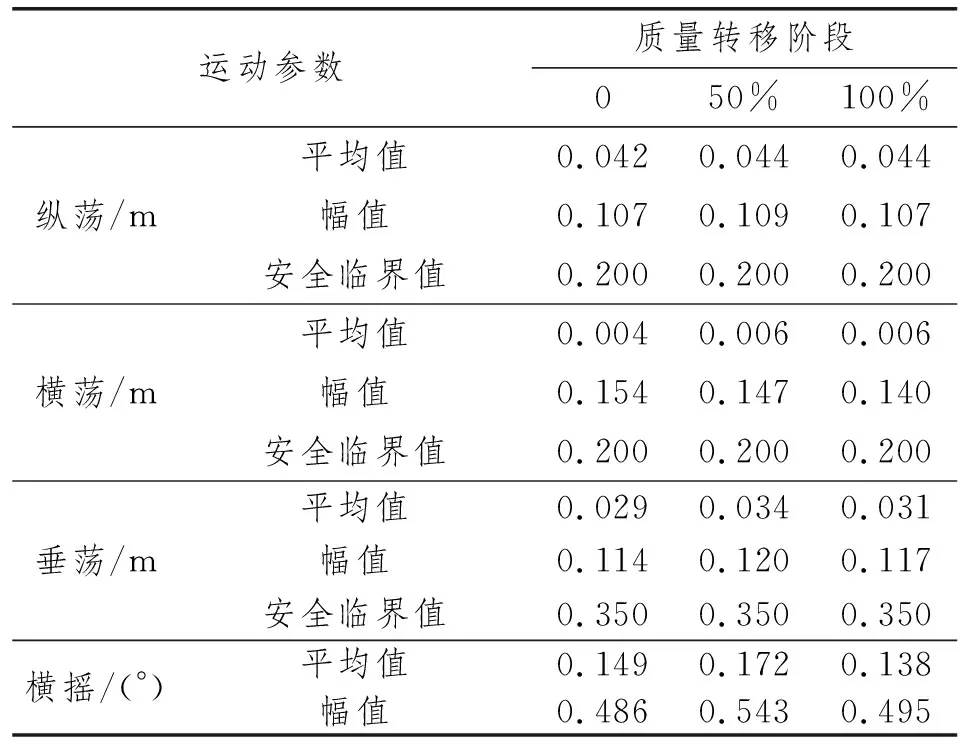
表4 质量转移各阶段驳船运动情况
对比表4中相关数据可知,不同质量转移阶段对驳船纵荡运动的影响较小。随着质量转移完成,DMU的约束作用可以完全生效,因此驳船在质量转移完成时横荡最小;但是由于波浪作用,在质量转移完成50%时驳船的横摇角会有明显的增大。由于平台上部组块质量转移到驳船,驳船的重心和吃水会发生变化,因此在质量转移50%时驳船的垂荡运动明显增大,质量转移完成后恢复至正常大小。上述幅值均未超过设定的安全临界值。
通过时域计算获得平台上部组块质量转移阶段为0、50%、100%等3个阶段的DMU水平与竖直方向的合力,并分别提取其平均值、最小值和幅值,结果如表5所示。

表5 质量转移各阶段DMU受力情况 kN
质量转移刚开始阶段DMU会因为波浪作用在水平和竖直方向有较小的碰撞受力。当质量转移为50%时,其水平方向的受力明显高于质量转移完成时的受力,这是因为质量转移过程中插肩对接会产生相对运动。分析竖直方向DMU的受力可知,由波浪引起的纵荡运动会导致驳船和组块之间在竖直方向受力会有2%~3%的变化,因此要求DMU在实际施工时具有一定的抗冲击能力。
3 水池模型试验
在水池模型试验中,对DMU与LSU的对接装置进行改良,使其在水平方向与竖直方向均有一定的缓冲能力,该装置与实际甲板对接单元满足几何相似条件。同时,在甲板对接单元内部的垂向和横向弹簧能够模拟实际甲板对接单元在各方向上的刚度特性。对接装置如图8所示。
图9和图10为试验所用驳船模型的外形与作业时的工作状态。

图8 DMU与LSU的对接装置

图9 k-class水池模型

图10 双船作业时工作状态
试验条件选取有义波高Hs=0.75 m,谱峰周期Tp=6.00 s,角度为180°,时长为1 500 s,将数据转化为幅值谱,在换算后将驳船运动和DMU受力与数值计算的幅值谱进行比较作图,结果如图11所示。

图11 驳船运动幅值谱对比
由频谱对比可知,船体运动响应在圆频率为0.8~0.9 rad/s达到峰值。在数值计算与水池模型试验中驳船的运动对于波浪的响应较为一致,但是由于水池模型试验中测量设备的振动与杂波的干扰,水池模型试验会有高频持续响应,但是在低频处二者响应基本吻合。纵摇运动的幅值没有超过0.30 m,横摇运动的幅值没有超过0.20 m,垂荡运动的幅值没有超过0.15 m,横摇角度各组成成分的幅值在0.5°以内,说明DMU和LSU的相对运动在允许范围之内,且数值计算结果能够较好地模拟质量转移完成时的运动状态。
DMU水平与竖直方向所受合力幅值谱对比如图12所示。
由频谱对比可知,DMU受力的响应在圆频率为0.8~0.9 rad/s达到峰值。在数值计算与水池模型试验中DMU的受力响应较为一致。但是由于水池模型试验中测量设备的振动与杂波的干扰,水池模型试验会有高频的持续响应,但在低频处二者响应基本吻合。在水平方向上由于系统整体运动幅度不大,水平方向受力各组成成分的幅值在2.5×104N以内。由于纵荡导致系统在竖直方向存在加速度,因此会导致纵向存在超出上部组块原有重力的受力响应成分存在,但是并没有超过1.5×107N,增加的成分不足10%,在DMU、LMU与驳船的承受范围之内。

图12 驳船运动受力谱对比
4 过驳阶段3船耦合计算分析
在完成质量转移后,需要将平台转移至另一驳船,为表述方便称其为x-class。这一阶段由于各个驳船之间距离非常小,因此需要着重考虑此过驳阶段3船之间的耦合关系。同样采用Sima软件进行水动力耦合时域计算,建立水动力模型如图13所示。
根据得到的时域数据分别提取3船横向各运动的幅值,结果如表6所示。
在实型值中,x-class与k-class之间距离为6 m。此过驳阶段3船在水平方向由平动和转动引起的横向运动叠加之后不超过0.6 m,也就是不超过驳船横向间距的10%。因此认为在海况良好时驳船在过驳阶段相互不会产生碰撞,可安全完成施工。

图13 3船耦合水动力模型

表6 过驳阶段3条驳船的运动情况
5 结 论
对导管架进行逆向浮托法拆除试验,分析质量转移分别为0、50%、100%时驳船和DMU的运动及受力响应。建立动态时域数值模型,并通过DNV Sesam中的Sima水动力分析组件进行计算。时域计算得到的对比结果显示,3个质量转移阶段的运动和受力幅值均未超过安全范围。经过对比,数值计算结果与水池模型试验结果基本统一,且频谱相似度较高,并且运动与受力响应都在允许范围内。通过3船水动力耦合计算,证明当过驳阶段3船位置较为靠近时,3船之间不会出现碰撞现象,在天气情况符合施工要求时,双船浮托逆向拆除法可以在实际施工中完成任务。
本次水池试验与DP系统结合是一次具有创新性的尝试,这次试验将会给以后同类试验研究提供重要的指导意义。
