Parametric Stability Analysis of Marine Risers with Multiphase Internal Flows Considering Hydrate Phase Transitions

LIANG Weixing, and LOU Min

College of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China

Abstract This study investigates the effects of multiphase internal flows that consider hydrate phase transitions on the parametric stability of marine risers. A numerical model of the multiphase internal flow that considers a hydrate phase transition is established.The model first solves the flow parameters and subsequently obtains the natural frequencies of risers with different gas intake ratios.The stability charts of marine risers with different gas intake ratios are plotted by applying Floquet theory, and the effects of the gas intake ratio on the instability and vibration response of the risers are identified. The natural frequency increases with an increase in the gas intake ratio; thus, instability zones move to higher frequency ranges in the stability charts. As the increasing gas intake ratio reduces the damping effect of the Coriolis force, the critical amplitude of the heave in the unstable region decreases, especially when hydrodynamic damping is not considered. As a result, higher-order unstable regions are excited. When in an unstable region, the vibration response curve of a riser with a high gas intake ratio excited by parametric resonance diverges quickly due to parametric resonance.

Key words hydrate phase transition; marine risers; multiphase internal flow; parametric stability; vibration response

1 Introduction

In recent years, offshore oil and gas development has gradually shifted toward deep sea or even ultradeep sea regions, thereby posing a considerable challenge to marine riser systems. During the service period of a riser, the periodic heave motion of the top floating platform due to waves changes the axial force acting on the riser, thus leading to the parametric vibration of the risers. Parametric resonance is an unstable vibration caused by parametric excitation, which leads to the exponential increase in the vibration amplitude with time, thus causing damage to the risers (Heet al., 2018).

In the past few decades, the dynamic behavior of marine risers subjected to internal and external fluid flows has received considerable attention from many scholars. Based on the principle of virtual work energy, Kaewunruenet al.(2005) developed a structural model of marine risers,including axial deformation, bending, effective tension,and external forces, and also both the riser and the internal fluid motions. Zhanget al.(2015) investigated the axial and transverse coupled vibration law of a deep water toptensioned riser under the combined effects of the internal fluid flow, external waves, and current loads. Heet al.(2017) conducted a theoretical investigation on an elastic and slender fluid-conveying pipe with a top-end excitation subjected to uniform cross flows and examined the combined effects of internal flow on the nonlinear VIV dynamics of pipes. Jianget al.(2019) numerically investigated the multimodal responses of pinned-pinned risers under the combined action of internal and external fluid flows and found that internal fluid velocities can influence the coupled frequencies and damping ratio for cross-flow and in-line motions. Xieet al.(2019) derived the governing equations for the vibration of pipes that convey variable-density fluid and analyzed the influence of the internal varying fluid density on the VIV of the pipe. Cabrera-Miranda and Paik (2019) investigated the nonlinear planar vibrations of a steel lazy wave riser excited by a slug flow and constructed frequency-response curves for curvature, effective tension, fatigue damage, and usage factor.

The parametric stability of marine risers has been widely studied by many scholars. Fujiwaraet al.(2011) used a large-scale model test to study the effects of parametric excitation on vortex-induced vibration. Yanget al.(2013)predicted the parametric instability of a top-tensioned riser in irregular waves and found that the higher vibration mode tends to fall into an unstable zone when a multifrequency excitation method is adopted. Leiet al.(2014)used the Floquet-Liapunov theorem to estimate the stability of a vibration system in the space of parametric excitation and discussed the influence of the parametric excitation on the frequency domain responses of the riser.Wanget al.(2015) presented a coupled dynamic analysis of a marine riser under combined forcing and parametric excitation, riser vibration response, bending moment, and shear force under the sea current; the combined action of sea current and sea wave was also investigated. Menget al.(2018) studied the effects of internal flow-induced centrifugal and Coriolis force on the parametric instability of deep water drilling risers and found that Coriolis force can make the combination resonance much more profound.

However, internal flow is not a steady single-phase flow,whereas a multiphase flow always includes oil, gas, and water. Given the low temperature and high pressure in deep water risers, natural gas and water are prone to producing hydrates, which decompose into natural gas after leaving the stable hydrate region. Therefore, the internal flow is a multiphase flow with hydrate phase transitions.Most studies on the dynamic characteristics and responses of marine risers have focused on uniform flows while considering internal flow. Moreover, a few scholars have considered the effects of internal flow on the parametric stability of marine risers. The previous work, which presented a dynamic analysis of marine risers subjected to external and multiphase internal fluid flows, has been cited in the literature (Lou and Liang, 2020). The present study examines the effects of multiphase internal flow parameters on the parametric stability of marine risers to avoid the occurrence of parametric resonance.

This paper is organized as follows: In Section 2.1, we establish a numerical multiphase internal flow model by considering hydrate phase transitions. In the model, the flow parameters are solved using the finite difference method. Subsequently, the parameters of the multiphase internal flow are introduced into the parametric excitation vibration equation in Section 2.2. Lastly, the effect of the multiphase flow that considers hydrate phase transitions on the parametric stability and vibration response is discussed in Section 3.

2 Numerical Model

2.1 Model of Multiphase Flow

Multiphase internal flow is a multiple-phase and multiple-component mixing system that arises due to hydrate phase transitions. In this work, a numerical model of multiphase internal flow that considers hydrate phase transitions is presented.

2.1.1 Phase transition model of natural gas hydrates

1) Phase equilibrium model

The Chen-Guo model is based on statistical thermodynamics theory, which has good accuracy and wide applicability, and easily converges to a solution. Hence, the Chen-Guo model is used in this work to obtain the phase equilibrium conditions of natural gas hydrates (Chen and Guo, 1998).

The equations of the Chen-Guo model are given in Eqs.(1) and (2).

whereflis the fugacity of the gas,f0lis the minimum fugacity required for the pure gas and pure water to form a stable hydrate when the system pressure approaches zero,θ1lis the occupancy rate of guest molecule l in a type-1 cavity,C1lis the Langmuir constant of guest molecule l in the type-1 cavity, andαis a constant of guest molecule l in the type-1 cavity.

2) Hydrate formation model

The gas hydrate formation process, which is considered a problem of hydrate shell formation on a droplet’s surface that gradually expands inward, is shown in Fig.1. On the basis of Vysniauskas & Bishnoimodel’s model (Vysniauskas and Bishnoi, 1983; Dholabhaiet al., 1993), the hydrate formation rate equation expressed by methane gas consumption is shown in Eq. (3).

whereuhis the methane consumption rate;Kfis the hydrate formation rate constant;Ais the cross-sectional area of the riser;d0is the diameter of the droplet;Ew0is the water content at the beginning of hydrate formation;Ewis the water content in the cross-sectional area; ∆Eais the activation energy;Ris the gas constant;Tis the temperature;Pis the pressure; ∆Tis the undercooling, where ∆T =Tc−T,Tcis the phase equilibrium temperature; anda,b,andγare experimental constants.

Fig.1 Schematic of the hydrate formation process.

3) Hydrate decomposition model

A schematic of the hydrate decomposition process is shown in Fig.2. This process is considered a problem of isometric sphere ablation from outside to inside. The solution to the hydrate decomposition rate is based on the Kim-Boshini hydrate decomposition kinetics model (Kimet al., 1987). The gas production rate of hydrate decomposition is given in Eq. (4).

wherenhis gas production rate;Kdis the hydrate decomposition rate constant;EWDis the water content at the beginning of hydrate decomposition;Ehis the volume fraction of the hydrate in the cross-sectional area; andfeqandfloare the reaction equilibrium and local gas fugacity,respectively.

2.1.2 Governing equations of a multiphase internal flow

1) Mass conservation equations:

2) Momentum conservation equations:

3) Energy conservation equations:

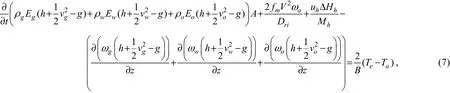
wherevg,vw,voandvhare the velocity of the gas, water, oil,and hydrate, respectively;ρg,ρw,ρoandρhdenote the density of the gas, water, oil, and hydrate, respectively;Eg,Ew,EoandEhare the volume fractions of the gas, water, oil,and hydrate, respectively;xgis the gas mass fraction in the hydrate;uhis the hydrate formation/decomposition rate;fris the frictional pressure drop;Pis the pressure in the riser;ωg,ωw, andωoare the mass production rates of the gas, water, and oil, respectively;his the enthalpy, which consists of the internal energy and pressure energy;vmis the velocity of mixture;Driis the inner diameter of the riser;ωais the mass flow of the fluid,Mhis the average molecular weight of the hydrates; ∆Hhis the hydrate phase transition heat;TaandTedenote the temperature in the riser and the ambient temperature, respectively;gis the acceleration of gravity;Cais the specific heat capacity of the fluid;Drois the outer diameter of the riser; andUais the convective heat transfer coefficient between the fluid and the environment.

Furthermore,Bin Eq. (7) can be calculated as shown in Eq. (8).

2.1.3 Solutions to the governing equations

The theoretical model of a multiphase internal flow involves many variables, making it difficult to obtain its analytical solution; thus, the established model must be discretized to obtain its numerical solution. In this study,the finite difference method is used to solve the equations.The temporal domain consists of the entire process starting from the riser’s entrance and ending at its exit; the spatial domain is the entire riser (Fig.3).

2.1.4 Definite conditions

1) Definite conditions of the temperature

The initial condition of the instantaneous temperature field (Weiet al., 2016) is a temperature field calculated at a steady state, and the boundary condition is the fluid temperature at the inlet of the riser. Thus, the definite conditions of the temperature are given in Eq. (9).

whereHis the water depth,Teis the seawater temperature,andTiis the temperature of the inlet fluid.

Fig.2 Schematic of the hydrate decomposition process.

Fig.3 Discrete schematic of the solution domain.

2) Definite conditions of the pressure and flow parameters

Under the assumption that the flow rate of each phase at the riser inlet is a constant, the pressure at the riser outlet can be measured directly. The definite conditions of the pressure and flow parameters are given in Eq. (10).wherezis the location along the riser;tis the time;ρlis the mixture density;Fris the friction pressure drop;qgi,qoi,andqwiare the flow rates of the gas, oil, and water at the riser inlet, respectively; andPiandPoare the values of pressure at the riser inlet and outlet, respectively.

2.2 Model of Vibrations Under Parametric Excitation

The riser model investigated in this study is shown in Fig.4. In the Cartesian coordinate system, the origin is at the bottom of the sea;His the water depth,Lis the length of the riser,zis the vertical coordinate of the riser’s element, andv=x(z,t) represents the displacement due to the parametric excitation at different positions and at different times. The differential arc length of the riser element after deformation is given in Eq. (11).

where dxand dzrepresent the lengths of the riser units in different directions, respectively.

Then, the geometric nonlinear terms'can be calculated as shown in Eq. (12).

Fig.4 Diagram of a marine riser.

The vibration equation under parametric excitation for the riser is the partial differential equation (Eq. (13)) shown below:

whereEis the elastic modulus,is the moment of inertia,Viis the velocity of the internal flow,andcis the hydrodynamic damping coefficient. ‘ · ’ indicates differentiation with respect to time, whereas ‘'’ indicates differentiation with respect toz.

Next,m=mr+mi+ma, where the mass per unit length of the riser isthe mass per unit length of the internal fluid is, and the added mass per unit length iswith added mass coefficientCa= 1.0.T(z,t) is the effective tension, which can be obtained as

whereT(z) is the static part of the effective tension and is given as

whereT0is the top tension, andwis the effect weight per unit length of the riser.

Then,

whereTtis the dynamic part of the effective tension,which is the tension of the riser over time caused by the heave motion of the platform;kis the equivalent spring stiffness of the tensioner;ais the platform heave amplitude, and Ω is the platform heave frequency, both of which contribute to the parametric excitation of the riser.

Assuming that the ends of the riser are hinged, the boundary conditions are as follows:

Regardless of the effects of the environmental loads, Eq.(13) can be reduced to a second-order ordinary differential equation using Galerkin’s method according to Louet al.(2019). A solution to Eq. (13) can be written as

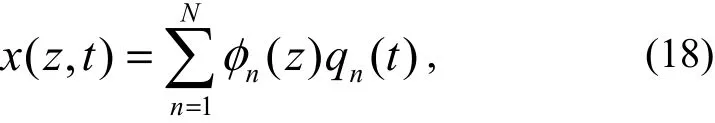
whereNis the number of adopted eigenfunctions;nis the mode order;φn(z) is the mode shape function, which represents the displacement amplitude of then-th normal mode;andqn(t) is a time function related to vibration response.

The riser model in this study is theoretical; thus, its mode shapes are as follows:

In reference to Menget al.(2018), the resulting secondorder implicit ordinary integral-differential equations can be achieved as

where

Then, a finite system of 2Nfirst-order coupled equations can be obtained as

where

wheremnmis the element of the mass matrixM,cnmis the element of damping matrixC,knmis the element of the stiffness matrixK, andn,m= 1, 2, ···,N. When omitting the time-varying component, the natural frequencies of the riser can be obtained. The parametric vibration equation is transformed into

whereA(t) = −[B]−1[E], and the period is 2π/Ω. Floquet theory is adopted to deal with parametric stability by using the periodic matrixA(t). Floquet theory provides a quantitative measure of the stability of a system of firstorder differential equations. The assumption Φ(t, 0) is the state transition matrix at an arbitrarily chosen moment in time, which is given by

The state transition matrix at the end of one period Φ(T,0) can be computed numerically by integrating the matrix differential equations over one periodT= 2π/Ω with the initial condition. Furthermore, the stability criterion can be defined as Re(λi)2+ Im(λi)2＜ 1 (i= 1, ···,N), whereλiare the eigenvalues of the state transition matrix at the end of one period.

2.3 Program Verification

In accordance with the established numerical model of the multiphase internal flow and the vibration equation of the marine riser, a program was developed on the basis of MATLAB. Furthermore, we validated the correctness of this program by calculating the internal pressure and natural frequency with the parameters given by Montoya-Hernandezet al.(2014). The parameters of the multiphase internal flow are shown in Table 1, and those of the dynamic analysis of the risers are shown in Table 2. The results of this program were then compared with data in the literature. Fig.5a shows that the internal pressure predicted by the internal flow analysis model in this study is consistent with that predicted in the literature, and the maximum error is less than 4.4%. Such a small error is obtained because the influence of hydrate phase transitionon pressure is considered in our internal flow model; hence,the predicted internal pressure is smaller. Fig.5b shows that the calculated results of the first- to fifth-order natural frequencies of the risers from the proposed dynamic model and the model in the literature are basically the same, and the maximum error is less than 2.1%.

Table 1 Parameters of the multiphase internal flow

Table 2 Parameters used in the dynamic analysis

Fig.5 Verification of the internal pressure and natural frequencies. (a) Internal pressure; (b) First- to fifth-order natural frequencies.

3 Results and Discussion

3.1 Analysis of the Flow Parameters of the Multiphase Internal Flow

The internal flow was modeled as a multiphase and multicomponent mixing system with hydrate phase transitions.In this part, we study the phase transition region of hydrates, as well as the effects of varying the multiphase flow parameters during the flow process from the underwater wellhead to floating platform, as shown in Table 3.

Table 3 Parameters used in the proposed model

Fig.6a shows the internal and phase equilibrium temperatures under different gas intake ratios. The intersection point between the internal temperature and phase equilibrium curves is the critical point of the hydrate phase transition. Below this critical point, the hydrate is in the formation region; above the critical point, the hydrate is in the decomposition region. Fig.6b displays the heat produced by friction between the internal flow and the wall,the hydrate phase transition and the heat transfer between the internal flow, and the external seawater when the gas intake ratio is 20%. The internal temperature is mainly affected by the heat transfer from the external seawater,whereas the hydrate phase transition and the friction between the internal flow and the wall have minimal influence on the internal temperature.

Assuming that the inlet temperature of the internal flow is 10℃, the internal temperature decreases when the external seawater temperature is lower than the internal temperature, thus reaching the lowest value at 900 m below the water’s surface. The inlet temperature then rises with the rapid increase in the sea water temperature near the water’s surface, thus reaching a maximum at the outlet.Fig.6a shows that the outlet temperature at gas intake ratios of 10%, 20%, 30%, and 40% are 17.97℃, 17.43℃, 17.04℃, and 16.67℃, respectively. That is, when the inlet temperature is the same, the higher the gas intake ratio, the lower the outlet temperature. This result is obtained because as the gas intake ratio increases, the internal flow velocity increases (see Fig.6c), resulting in a decrease in the heat transfer time. Simultaneously, an increase in gas volume fraction decreases the specific heat capacity and thermal conductivity of the internal flow, both of which reduce the heat transfer between the internal flow and the external sea water. Therefore, at the same inlet temperature, the temperature of a low gas intake ratio is close to the ambient temperature.

Figs.6c–f show the changes of the velocity, acceleration,density, and pressure, respectively, at different gas intake ratios. As the fluid flows upward, the gas expansion and hydrate decomposition increase the gas volume fraction,the mixed phase velocity, and the acceleration and decrease the density. The low density causes the gravity pressure to decrease, whereas the high velocity caused by the high gas intake ratio increases the frictional pressure drop rate.However, the effect of the gravity pressure drop is much greater than the frictional pressure drop, resulting in a net decrease in the total pressure drop. When the riser outlet pressure remains unchanged, the overall internal pressure decreases. Therefore, the phase equilibrium curve shifts to the left, and the hydrate formation region descends in depth. Simultaneously, hydrate formation consumes gas and slows down the change of the flow parameters caused by gas expansion. In the hydrate decomposition region,gas generated by hydrate decomposition accelerates the changes of the multiphase flow parameters, especially near the water’s surface.

Fig.6 Flow parameters at different gas intake ratios.

According to the above discussion, the flow parameters,such as velocity, acceleration, density, and pressure, constantly change in the upward flow. Changes in the flow parameters affect the stiffness, mass, and damping matrices in the discrete vibration differential equation of the riser. In the next section, the effect of the multiphase internal flow on the dynamic characteristics and response of the riser is further discussed on the basis of the calculated results given in this section.

3.2 Effect of the Gas Intake Ratio on the Natural Frequencies of the Riser

Figs.7a–d are the first-, fifth-, tenth-, and fifteenth- order natural frequencies of the riser for constant flow velocities (v= 0 m s−1andv= 0.79 m s−1) and gas intake ratios(10%, 20%, 30%, and 40%). When the internal flow is purely liquid and the velocity is constant (v= 0 m s−1andv= 0.79 m s−1), the first-, fifth-, tenth- and fifteenth-order natural frequencies decrease with the increase in the internal flow velocity. However, when the velocity increment is small, the natural frequency of the riser decreases slightly,which is consistent with the conclusions of Montoya-Hernandezet al.(2014). When the fluid in the riser is a multiphase flow arising from the hydrate phase transitions,the natural frequencies of the riser at different gas intake ratios are obtained on the basis of the calculated results of the internal flow parameters presented in Section 3.1. The results show that the natural frequencies of risers in the first, fifth, tenth, and fifteenth modes increase with the increase in gas intake ratio. The natural frequencies of different modes show similar regularity with an increase in air volume, but the trend of increasing natural frequencies with an increase in gas intake ratio is more evident in the higher modes. According to the results given in Section 3.1, the presence of gas increases the velocity of the internal flow, causing the natural frequency to decrease. However, the presence of gas simultaneously causes the pressure, density, and acceleration to increase, resulting in an increase in natural frequency. Thus, when the fluid in the riser is a multiphase flow with hydrate phase transitions,the natural vibration frequency of the riser generally shows an increasing trend with an increase in gas intake ratio.

Fig.7 Natural frequencies of the riser. (a) First-order; (b) Fifth-order; (c) Tenth-order; (d) Fifteenth-order.

3.3 Effect of Gas Intake Ratio on Parametric Stability

For a top tension riser in deep water, Ω = 2ωn/Pdetermines the order of instability. In general, unstable regions with large orders must meet complicated conditions, and high-order unstable regions are less likely to occur. Therefore, a high-order unstable region has no effect on the vibration response of the riser. The first two parameters of the unstable region in the project play a key role in the safety of the riser. Only the first (P= 1, Ω = 2ωn) and second instability regions (P= 2, Ω =ωn) are investigated in this study.

Assuming that the wave period is 3–13 s (the frequency is 0.48–2.09 rad s−1), the tenth-order natural frequency of the riser corresponds to 2 rad s−1in accordance with the results given in Section 3.2. The period of a parametric instability region corresponding to high-order modes is small; thus, this part mainly considers the stability analysis of the first eight order modes, where the range of calculation is 0.1–2 rad s−1.

To investigate the effect of the gas intake ratio on the stability of the riser, we calculate riser stability in accordance with Floquet theory, as presented in Section 2.2; a MATLAB program, which uses the Runge-Kutta method to solve the initial value problem and the corresponding eigenvalues of this matrix, is used. Red, green, and blue dots are used to represent the parametric instability conditions when the gas intake ratio is 0%, 20%, and 40%,respectively. The unstable regions represented by the dots are the results of the superposition of multiorder instability regions under different modes. The stability charts without hydrodynamic damping is shown in Figs.8a–c. In reality, the riser is surrounded by water. The resistance caused by the surrounding water is referred to as fluid drag, and the stability charts with hydrodynamic damping are shown in Figs.8d–f.

Fig.8 Stability charts of the riser.

As shown in Figs.8a–c, the unstable region without hydrodynamic damping consists mainly of first- and second-order unstable regions. Given the partial coincidence of the first- and second-order unstable regions, the second-order unstable region (ω2,ω4,ω6) cannot be fully displayed. When comparing Figs.8a–c with Figs.8d–f, the second-order unstable region disappears, and the firstorder unstable region decreases in the latter when considering hydrodynamic damping. With an increase in gas intake ratio, the unstable regions move to the high- frequency range in the stability charts; that is, under the same heave amplitude, the heave frequency of an unstable region with a high gas intake ratio increases. This phenomenon can be explained by the natural frequencies of the riser increasing with an increase in gas intake ratio, as shown in Section 3.2. Moreover, Fig.8 shows that the critical amplitude of heave in the unstable region decreases with an increase in gas intake ratio, especially when hydrodynamic damping is not considered, that is, when high-order unstable regions are excited with the increasing gas intake ratio.This result is caused by the increase in gas intake ratio,resulting in the reduction of internal flow density and increase in internal flow velocity. Given the combined effect of these two factors, the Coriolis force decreases; consequently, the areas of the instability zones can be increased by damping the Coriolis force.

3.4 Effect of Gas Intake Ratio on the Vibration Response

The parametric excitation stability charts of risers with different gas intake ratios with and without hydrodynamic damping are shown in Fig.8. With the 0.1 hydrodynamic damping stability charts taken as an example, the vibration response of the risers with different gas intake ratios under parametric excitation are obtained. The parameters of the heave frequency and the amplitude in the stable and unstable regions of the riser stability chart with different gas intake ratios (Fig.8f) are selected, and the dynamic response is calculated using our MATLAB program. The initial conditions are

Figs.9a–c show that when the platform heave frequency is twice the third natural frequency of the riser and the heave amplitude is 1 m, the first eight modes of the riser are not excited by parametric excitation for intake ratios of 0%, 20%, and 40%, and the response curves gradually attenuate with time; therefore, the riser is stable.Meanwhile, Figs.9d–f show that when the platform heave frequency is twice the third natural frequency of the riser and the heave amplitude is 3 m, the parametric response of the riser for gas intake ratios of 0%, 20%, and 40% is unstable, and the vibration response curve of the third mode represented by the red curve increases exponentially with increase in time. This phenomenon occurs because the above parameter combinations are in the unstable regions of the riser stability chart in Fig.8f; thus, the third mode is excited, resulting in the loss of stability of the riser and parametric resonance. Given that the modes of the riser model are not coupled, the other modes are not excited and gradually attenuate over time. As shown in Figs.9d–f, the third mode response curves of the high gas intake ratios diverge faster due to the decreased damping and increased natural frequency. That is, a riser with a high gas intake ratio is damaged early due to parametric resonance when the parameter combinations are in the unstable regions.

4 Conclusions

In this study, a multiphase internal flow numerical model that considers hydrate phase transitions was established.The flow parameters of the model were solved, and the natural frequencies of risers with different gas intake ratios were obtained. According to Floquet theory, stability and parametric vibration response analyses of risers under different gas intake ratios were conducted, and the following conclusions can be drawn:

1) From the riser’s inlet to its outlet, the pressure and density of the internal flow decrease, whereas the velocity and acceleration increase. In the hydrate formation region,the flow parameters change slowly because hydrate formation consumes gas. In the hydrate decomposition region,hydrate decomposition increases the gas volume fraction and accelerates the changing trend of the flow parameters.Simultaneously, the pressure and density of the internal flow decrease, whereas the velocity and acceleration increase with the increase in gas intake.

2) Natural frequency decreases with the increase in internal flow velocity. However, an increase in gas intake also changes other flow parameters, including acceleration, pressure, and density, thus resulting in an increase in the natural frequency of the riser where the changing trend is evident in higher modes.

3) The instability zones move to the high-frequency range in the stability charts with the increase in gas intake ratio. Such movement can be explained by the natural frequencies of the riser decreasing with the increase in gas intake ratio. Moreover, as the increased gas intake ratio diminishes the damping effect of the Coriolis force,the areas of the instability zones increase, and the critical heave amplitude in the unstable region decreases, especially when hydrodynamic damping is not considered.Consequently, additional high-order unstable regions are excited with the increase in gas intake ratio.

4) When the frequency and amplitude of the platform heave within the unstable region, the parametric resonance of the riser mode corresponding to the unstable region is excited, and the vibration response curve of the riser with a high gas intake ratio excited by parametric resonance without considering coupling effect diverges quickly due to parametric resonance.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (No. U2006226), the National Key Research and Development Program of China (No.2016YFC0303800), and the National Natural Science Foundation of China (No. 51579245).

Fig.9 Vibration response for different gas intake ratios and 0.1 hydrodynamic damping.