一种用于微电网经济调度的改进型内部搜索算法

陈汝科，沈丹青，何丽娜，杨凯帆，谢 枭，王若昕，黄 婧

（1.国网湖北省电力有限公司钟祥市供电公司，湖北钟祥 431900；2.国网湖北省电力有限公司沙洋县供电公司，湖北沙洋 448200）

引言

随着世界环境污染问题的日益严重，能源的再利用与综合利用成为了主流，可再生资源的利用研究得到了快速发展[1]。然而可再生资源的不稳定性也会影响电网的安全运行。为解决这一问题，微电网技术在现代电网运行中得到了迅速推广[2]。微电网是将电力系统中的分布式单元整合成一个独立的发电系统[3]。截止目前，在微电网经济优化调度方面，学者们常将研究重点放于优化算法改进，这是由于微电网的经济优化调度较为复杂，运用传统算法计算的难度较大。如文献[4]通过改进传统灰狼算法来解决微电网的优化问题；文献[5]提出了一种改进型布谷鸟搜寻算法来进行热电联供微电网优化调度；文献[6]利用内部搜索算法求解了微电网的经济排放调度问题，结果表明内部搜索算法在降低成本方面具有显著优势。

本研究对性能较好的内部搜索算法进行了有效改进，并在负荷响应侧引入了基于分时电价的数学模型，运用该改进优化算法对微电网进行经济调度，最终将计算结果与典型调度策略计算结果进行对比，以此验证本算法的有效性。

1 微电网模型

微电网模型主要包括电源模型及负荷响应模型[7]。

1.1 分布式电源模型

光伏电源的输出功率PG为[8]：

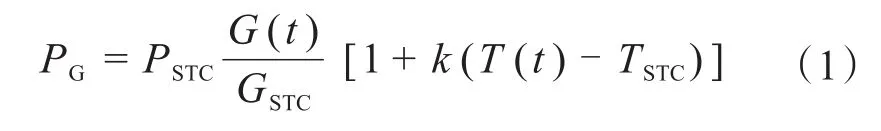
式中，PSTC为标准输出功率；GSTC为标准光辐射量；k为温差调节因子；T(t)为t时刻实时温度；TSTC为标准环境温度。

风机的输出功率PF为：

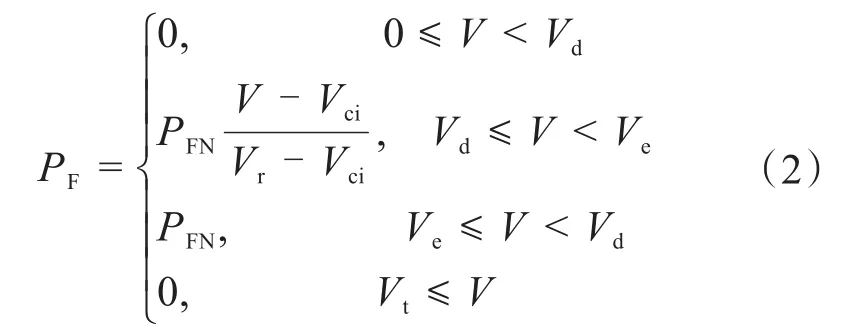
式中，Vd为最低风速；Ve为额定风速；Vt为停机风速。

柴油发电机其输出功率可表示为[9]：

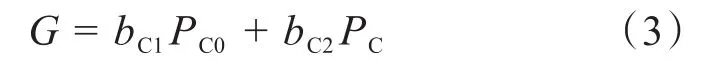
式中，G为耗油总量；bC1、bC2分别为耗量特性和运算斜率；PC0、PC分别为额定功率和实时功率。

燃料电池其输出功率可表示为[10]：

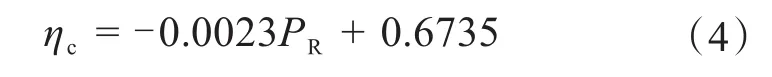
式中，ηc表示发电效率；PR表示输出功率。

对于蓄电池模型，其荷电状态SSOC(t)可表示为[11]：

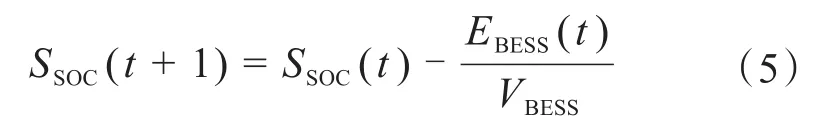
式中，EBESS(t)为t时段内储能系统的充放电电量；VBESS为储能总容量。

1.2 负荷需求响应模型

负荷需求响应指采取相关策略以使用户能够参与配电的过程，其目的是使用户能够合理分配不同时段的功耗，并减轻配电网络的压力。考虑到微电网的昼夜负荷差异较大，为平衡峰谷差异，引入了基于分时价格的负荷响应模型。

引入弹性理论对负荷用电量及时段电价二者变化关系进行分析，设置24为一个调度周期，根据弹性理论有：

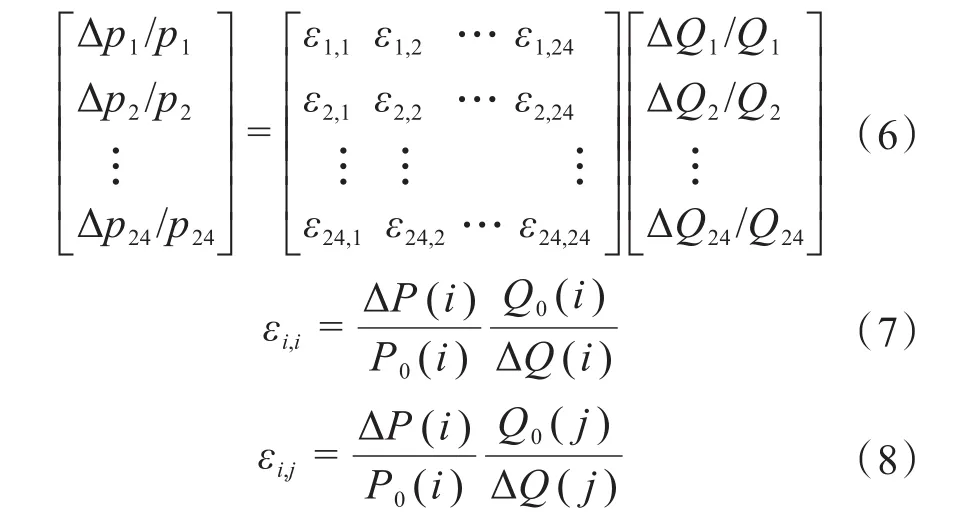
式中，ε为弹性系数；P0(i)为平移前的用电量；ΔP0(i)为平移前后电量之差；Q0(i)为正常使用时段的电价；ΔQ0(i)为平移前后的电价之差。

在供需平衡的条件下，负荷响应模型可表示为：

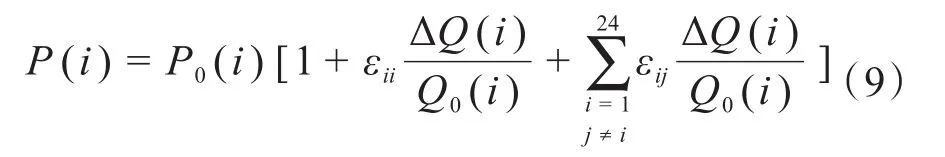
式中，P(i)为负荷实际需求。

1.3 目标函数的建立

分别以运行成本、环境污染费用最低为目标，建立经济模型。

以运行成本最低为目标，其经济模型为：

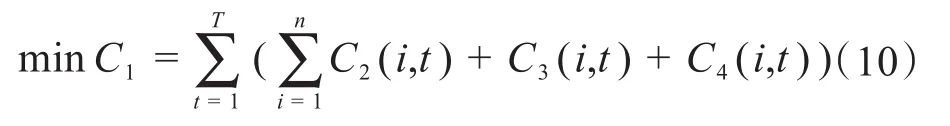
式中，C1为运行总费用；T为经济运行的时间段总数；C2(i,t)、C3(i,t)、C4(i,t)分别为发电单元的燃料费用、维护费用及折旧费用。

以污染费用最低为目标，其经济模型为：

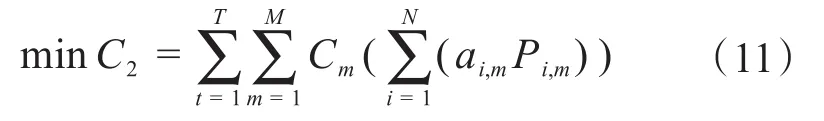
式中，M为气体种类数；Cm排放成本；ai,m为电源设备所排放污染气体m的系数。

1.4 约束条件的建立

（1）功率平衡

功率平衡可由下式求出：

式中，Pt为t时段的预测负荷功率；Pt、Pt、Pt、Pt、PtFGCXR分别为风机、光伏、柴油发电机、蓄电池、燃料电池的输出功率。

（2）蓄电池的荷电状态

式中，SSOCmin、SSOCmax分别为蓄电池允许的下限值和上限值。

（3）各电源设备的输出功率限制

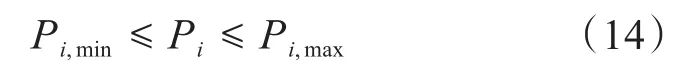
式中，Pi,min、Pi,max分别为电源输出功率的最小值和最大值。

2 改进内部搜索算法

2.1 ISA算法计算流程

ISA算法流程图如图1所示。由图1可以看出，ISA算法根据自适应系数α的取值，将元素分为了两组，分别是求解全局最优的成分组及求解局部最优的镜子组。因此，通过调节α的取值可以改变两组元素的数量比例，进而影响算法的收敛精度与速度。

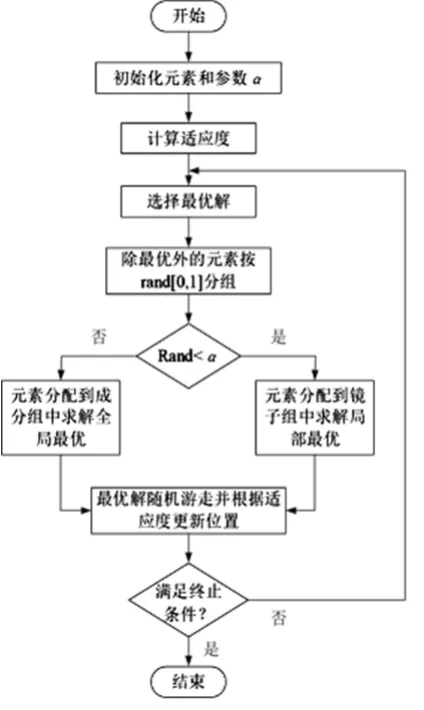
图1 ISA算法流程图

对于自适应系数α的取值，工程实际中通常有以下方法：①α取一个定值并且其不随环境变化而变化；②α设置为0.1～0.3内的随机值；③根据α可以影响收敛的特点，在每次迭代中改变α的取值，使算法性能更好。

为优化ISA的算法性能，选取第3种方法，对ISA算法进行了改进。

2.2 ISA算法改进

在对α进行取值时，当α取值较大，可以扩大优化范围，获得更多的解；当α取值较小，计算范围会缩小。因此，可以通过改进α的取值方法，即在迭代过程中，按照一定速度逐渐减小参数值。α可表示为：

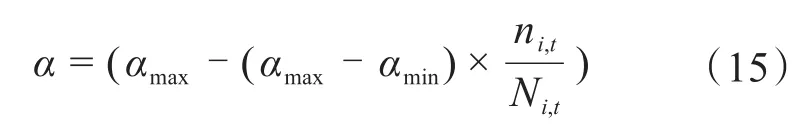
式中，αmax、αmin分别为取值的上限和下限；n为当前迭代次数；N为总迭代次数。

以上述分析为根据，可画出如图2所示的改进型内部搜索算法计算流程图。

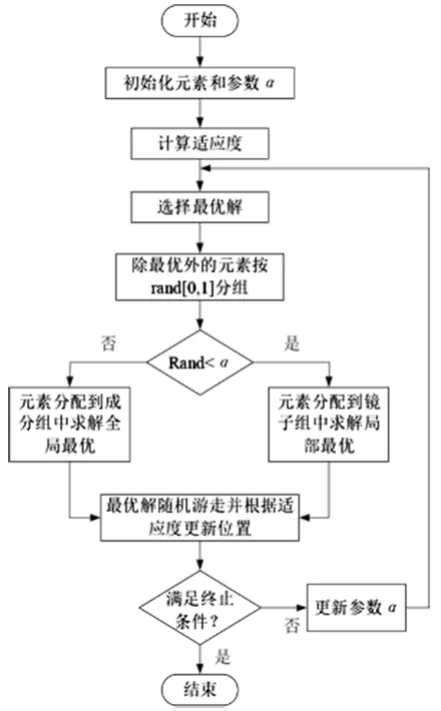
图2 改进型ISA算法流程图

对于边界条件，可做如下处理：

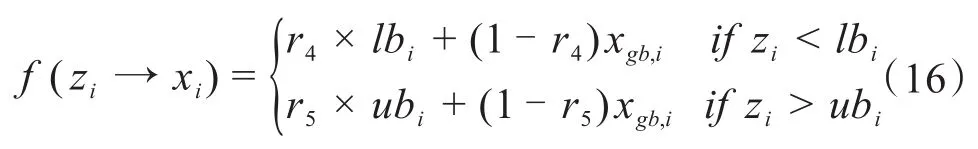
式中，r4、r5分别为0到1之间的随机值，xgb,i为全局最优解的相关成分。

3 算例分析

以运行费用最小为目标函数，分别求得典型调度策略与改进算法下电源设备的输出功率，如图3和图4所示。

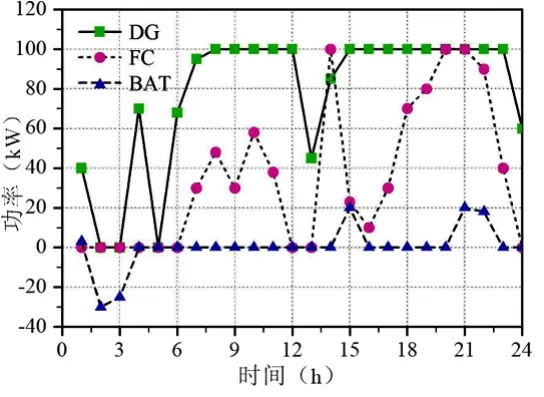
图3 典型调度策略下电源的输出功率

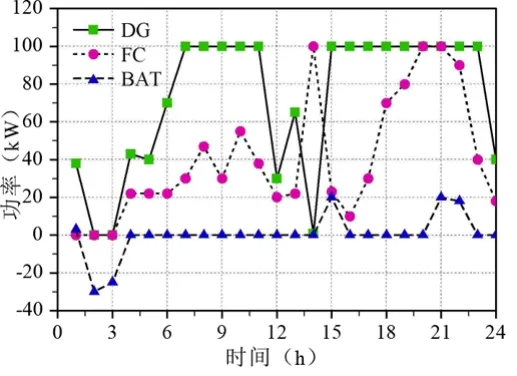
图4 优化调度下电源的输出功率

两种策略的荷电状态对比图如5所示。由图5可知，在运用典型专家策略进行微电网的优化调度时，蓄电池由于在1时段中没有释放电能，导致在3时段中产生弃电。并且在4、5、6、13时段中，忽略了燃料电池的电价变化，因此无法降低运行费用。

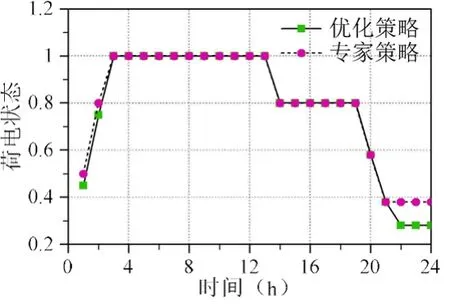
图5 荷电状态对比图

在考虑污染费用情况下，典型调度策略与改进优化调度策略下的荷电状态对比如图6所示。观察图6可知，当考虑污染费用时，典型调度策略依旧无法灵活调度蓄电池，并且在第20、21时段，典型调度策略中蓄电池仅作为备用输出设备。

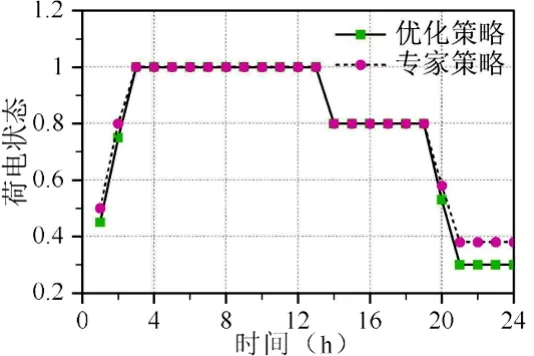
图6 荷电状态对比图

分别计算两种调度策略下的运行成本，结果如表1所示。

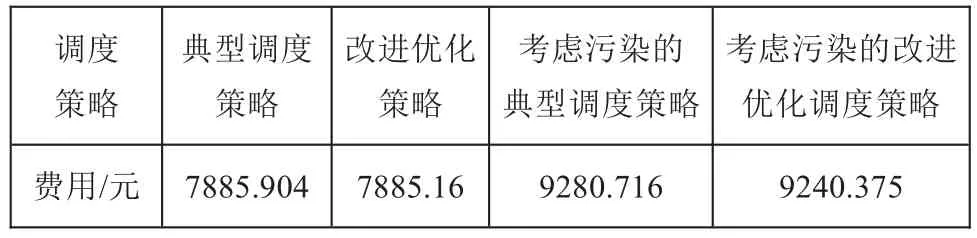
表1 2种调度策略的运行费用

由表1可知，改进优化调度策略在考虑污染和不考虑污染调度方面都可以有效提高微电网运行的经济性。综上可知，改进优化调度策略可以更好地发挥蓄电池的经济优势。

4 结论

（1）建立了包含光伏、风电、柴油发电机、燃料电池及蓄电池5种分布式电源模型，并引入基于分时电价的负荷需求模型以平衡负荷侧峰谷差异。

（2）通过对内部搜索算法进行改进，提出了一种改进型优化算法，通过算例对比分析，最终验证了优化算法的有效性。