网络断层扫描:理论与算法*

李惠康,高 艺,董 玮,陈 纯

(浙江大学 计算机科学与技术学院,浙江 杭州 310027)

随着互联网的飞速发展,网络在组成结构、数据流量和商业用途等方面变得越来越复杂.如何认知这些网络,对理解网络时代下用户行为有着重要意义.同时,这也是有效管理网络、保证可靠网络服务的基础.网络测量是指遵照一定的方法和技术,利用软硬件工具来测试、验证及表征网络性能和状态的一系列活动.网络测量可以是对网络性能的测量,如延时、丢包率、网络流量[1],也包括对网络拓扑[2]、路由信息等其他网络特征的测量.它是理解和认识网络行为的重要手段,在网络建模、网络安全、网络管理和优化等许多领域都有广泛应用[3].国内外学术界和研究机构对网络测量技术进行了大量的研究,总体上,这些网络测量技术一般采用分布式测量结构,在网络内部的相关节点上,通过测量代理采集有关测量数据,如报文丢失率、延迟和流量等,这些测量数据将汇集到一个中心节点上,通过建立适当的数学模型,对测量数据进行分析和计算,从而实现对网络系统的性能评估[4].这种网络测量技术属于网络内部测量,与网络体系结构和网络协议密切相关,并且需要网络内部相关节点的密切协作,具有较高的测量精确度.但也存在一些缺陷,主要表现在如下两个方面:(1) 网络测量依赖于特定的网络协议(如TCP/IP 协议、SNMP 协议),无法实现与网络结构和协议无关的测量;(2) 测量依赖于自治系统内部节点之间的协作,出于网络安全和商业利益等原因,有些自治系统并不对外开放,难以实现内部节点的协作和信息交流,无法保证测量准确性.

为此,近些年来,国际上许多学术机构都在寻求其他途径来研究网络的整体性能及其相互影响,将已成功应用于医学、地震学、地质勘探等领域的成熟理论和方法应用于通信网络领域,衍生出了网络断层扫描(network tomography)技术[5].它是根据网络外部(即网络边界)的测量信息来分析和推断网络内部的性能及状态,是一种在没有网络节点协作的条件下,通过主动发包探测或被动收集网络内部有用信息的新技术,结合数理统计方法,能够有效地推测出网络链路上的QoS 指标,如延迟分布、丢包率、吞吐率和流量等.

目前,网络断层扫描的研究主要集中于两个方面:一是测量数据的收集,主要研究如何收集网络内部相关的有用信息;二是测量数据的分析,主要研究如何根据收集的数据来获取网络内部的性能指标和运行状态.本文在简要介绍网络断层扫描基本概念和形式化表述的基础上,从测量数据收集和测量数据分析两个主要方面综述了网络断层扫描的研究现状与关键技术.随后分析了已有网络断层扫描方法在实际应用中的核心缺陷,并系统介绍了针对这些核心缺陷近年来提出的最新理论及算法.最后,基于现有研究成果对网络断层扫描技术的发展趋势和下一步的研究方向进行了讨论.

1 网络断层扫描基础

1.1 网络断层扫描的基本概念

网络断层扫描通过在网络边界上进行端到端(end-to-end)的测量,来推断网络内部状态和通信行为.为此,基于网络断层扫描的测量方法包含3 个主要步骤:①网络模型构建阶段,明确网络拓扑结构和网络性能模型;② 测量数据收集阶段,通过在网络节点或边界上部署具有监测能力的装置(即监测节点),并采用主动测量或被动测量的方式,从监测节点上收集端到端的网络测量数据;③测量数据分析阶段,根据网络性能模型建立性能推测方法,运用统计学理论对测量数据进行分析处理,从而推算出网络内部性能指标.

网络断层扫描技术对网络性能的推算依赖于监测节点的测量数据值,测量方式的不同,会影响到推算结果的准确性.根据测量过程中是否向被测网络中注入额外的数据包,网络测量方式可分为主动测量和被动测量[6].其中,主动测量通过向网络中发送特定的探测数据包,并通过分析探测数据包在网络中发生的特性变化,推算得到网络内部性能和行为参数,比如链路时延和丢包率等性能指标;被动测量通过在网络中部署监测节点(或数据包捕获器),收集网络节点或链路上的数据包信息,被动地监测网络,获知网络行为状况.被动测量方式不必向网络发送探测数据包,不会占用额外的网络资源.然而,被动测量要依赖所测量网络节点上的负载情况及测量链路上的通信流量,从而使得其可用性较差,实现复杂性高,难以保证测量的准确性.

当前,网络性能测量成为了网络断层扫描的一个主要研究目标.通过对网络时延、丢包率和吞吐量等性能指标进行数据采集和统计,分析网络特定范围或端到端路径的连通性及有效性,以便于发现网络瓶颈,优化网络配置,保障网络服务质量.此外,通过网络断层扫描测量得到的数据,可用于网络故障的定位,从而有助于网络维护管理.

1.2 网络断层扫描的形式化表述

为了便于网络断层扫描方法的研究与设计,通常需要对网络模型、测量目标和测量方法进行形式化的表述.下面将简要介绍网络断层扫描在这几方面常见的形式化表述方式.

首先,网络模型是网络断层扫描的基础,主要指在实现网络断层扫描技术时所采用的拓扑结构.为进行简洁的描述,可用G=(V,L)表示被测网络的拓扑结构.其中,V为网络节点集合,L为网络链路集合.每个节点表示一个计算机终端(terminal)、路由器(router)或者一个包括多个计算机/路由器的子网(subnetwork).任意两个节点间的连接称为路径(path),每条路径由一条或多条链路组成,任意两个节点之间的直接连接(不需要中间节点)称为链路(link),链路可以是单向的也可以是双向的.每条链路可以是一条物理链路,也可以是几条物理链路的抽象.对于如图1 所示的网络拓扑,其节点集合V={v1,v2,v3,v4},链路集合L={l1,l2,l3,l4,l5,l6},节点v1与v3之间存在5 条不经过重复节点的路径:l5,l2l3,l1l4,l2l6l4,l1l6l3.

Fig.1 A sample network topology图1 一个简单网络拓扑

为了获得端到端的测量数据,网络断层扫描方法需要在网络部分节点上部署监测节点.用集合M={m1,m2,…,mμ}表示网络部署的监测节点,在这些监测节点上可以发送和接收探测数据包.相应地,网络中其余的节点称为普通节点,用集合N(N=VM)表示.依赖于网络采用的路由策略,监测节点通过沿着某些测量路径发送探测数据包的形式,推算出网络节点及链路的性能指标和运行状态.在给定网络拓扑G和监测节点M的情况下,用集合P代表监测节点间的一组测量路径.需要注意的是,不同的路由策略可能会产生不同的测量路径集合.例如,当网络所有节点都运行了源路由机制(source routing[7])时,监测节点能够严格地控制和指定每一个探测数据包的路由路径.因此,在源路由机制下,测量路径P可以包含监测节点间任意形式的路径.相反,当探测数据包的路由策略完全由网络正常运行的路由协议决定时,测量路径P只能包含监测节点间一组特定形式的路径,如最短路径.

对于一个含有n条链路的网络G(即n=|L|),用表示G中的链路集合,以及用x=(x1,…,xn)T表示链路性能指标向量,其中,xi表示链路li的性能.给定监测节点间的一组测量路径,用c=(c1,…,cγ)T表示测量路径性能指标向量,其中,ci表示路径pi的性能.在很多网络应用中,链路性能指标是可以累加的(additive).例如,多条链路上的时延是单条链路时延之和;多条链路的原始丢包率虽然为单条链路丢包率的乘积,但在经过对数函数(log(·))转换后,也可以表示成单条链路丢包率累加的形式.对于可累加的链路性能指标,一条测量路径的性能值等于这条路径上所有链路性能值的总和.因此,我们可以用一个线性方程组的方式将已知的路径测量数据与未知的链路性能指标关联起来:

其中,R=(Rij)为一个γ×n阶的测量矩阵(measurement matrix),并且测量矩阵R的元素值要么为0,要么为1,即Rij∈{0,1}.具体地,当测量路径pi经过链路lj时,Rij=1;否则,Rij=0.因此,在数据分析阶段,网络断层扫描的目标是在给定R和c的情况下,通过求解线性方程组(1),获得链路性能x的值.

当链路li的性能指标xi在线性方程组(1)中有唯一解时,称链路li为可识别的(identifiable),否则称li为不可识别的(unidentifiable).另外,当网络G中所有链路都是可识别的,称网络G为完全可识别的(completely identifiable);否则,当网络G中只有部分链路是可识别的,称网络G为部分可识别的(partially identifiable).基于线性代数理论,只有当方程组(1)的测量矩阵R列满秩时(即rank(R)=n),网络G才能是完全可识别的.即:为了确切地计算出网络中n链路的性能x,网络断层扫描必须要获得监测节点间n条线性无关的测量路径的性能数据.

进一步地.当网络测量的目标是判断链路通信是否正常(即链路测量指标只有正常和失效两种状态)时,我们将用到布尔网络断层扫描方法(Boolean netowrk tomgoraphy).与常规网络断层扫描思想类似,布尔网络断层扫描通过测量监测节点间一组路径的状态,推断出网络内部链路的状态.形式化地,用x=(x1,…,xn)T表示链路状态向量以及c=(c1,…,cγ)T表示测量路径状态向量.与常规网络断层扫描不同的是,x和c为布尔向量,即元素xi和ci只有0 和1 两种取值.当xi=1(或ci=1)时,表示链路li(或路径pi)通信发生失效;反之,当xi=0(或ci=0)时,表示链路li(或路径pi)通信正常.考虑到对于一条路径pi,只有当pi包含失效链路时,pi才会发生通信失效,可以用如下方式将已知的测量路径状态信息与未知的链路状态信息关联起来:

其中,R=(Rij)为γ×n阶的测量矩阵(measurement matrix),并且元素Rij∈{0,1}.“⊙”为布尔矩阵的乘积运算,即.布尔网络断层扫描的目标是在给定R和c的情况下,通过求解布尔方程组(2),获得链路状态x.同理,当链路li的状态xi可以由方程组(2)唯一确定时,称链路li为可识别的(identifiable).

需要说明的是:虽然方程组(1)和方程组(2)表述的是对链路性能和状态的测量,但网络中节点的性能和状态可以等价转换为与其关联链路的性能和状态,所以网络断层扫描方法仍然可以用方程组(1)和方程组(2)的形式来求解网络节点的性能和状态.

1.3 网络断层扫描的简单例子

图2 所示为一个包含7 个节点和11 条链路(链路l1～l11)的网络拓扑,其中,m1,m2和m3为部署的3 个监测节点.为了测量出所有链路的时延,网络断层扫描方法在3 个监测节点之间构造了11 条测量路径p1～p11.其中,1 条为m1与m2间的测量路径,7 条为m1与m3间的测量路径,3 条为m2与m3间的测量路径.

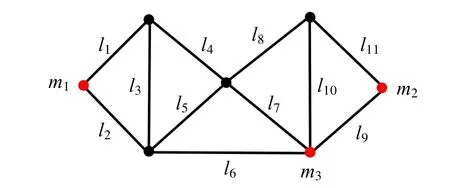
Fig.2 A network topology with three monitors:m1,m2and m3图2 部署3 个监测节点(m1,m2和m3)的网络拓扑

用向量x=(x1,…,x11)T表示链路l1～l11的时延,用向量c=(c1,…,c11)T表示测量路径p1～p11的时延,从而可以得到如下形式的测量矩阵R:

对于线性方程组Rx=c,由于测量矩阵R是列满秩的(即rank(R)=11),所以链路时延x有唯一解,即x=R-1c.在图2 中,尽管监测节点间还可以选取其他形式的测量路径(如l2l5l7l9),但这些额外的测量路径都是与已有测量路径(p1～p11)线性相关的,即,其他形式的路径都可以用已有路径(p1～p11)线性表示.因此,从链路性能测量的角度来说,p1～p11是一组最优的测量路径.此外,当我们任意移除一个监测节点(如m2)后,用剩余的7 条测量路径(p2～p8)构成的测量矩阵将不是列满秩的,即剩余的7 条测量路径将不能保证所有链路的可识别性.因此,从链路性能测量的角度来说,m1,m2和m3是一种最优的监测节点部署方式.

从图2 的例子中可以看出,监测节点部署和测量路径构造(或选取)对网络断层扫描方法的有效性有着重要的影响.下一节我们将详细综述国内外在网络断层扫描监测节点部署和测量路径构造等方面的研究进展.

2 相关工作

近些年,网络断层扫描作为网络测量领域的一个研究热点,得到了国内外学者的广泛关注.总体上,网络断层扫描包含网络模型构建、测量数据收集与测量数据分析这3 个主要步骤.其中,测量数据收集包含监测节点部署、测量路径构造与选取.本节从监测节点部署、测量路径构造与选取、测量数据分析与推断这3 个方面对近些年国内外代表性的研究工作进行归纳分析,其中也包含对各研究工作网络模型的阐述.

2.1 网络监测节点部署

如何获取网络内部的有用信息,是网络断层扫描研究的重要组成部分.当前,网络断层扫描的测量对象一般可分为网络状态参数和网络性能指标.其中,网络状态参数包含网络节点的配置信息和网络链路的状态信息,网络性能指标包括链路吞吐率、链路丢包率和链路时延等.这些指标反映网络的实时运行状态.根据测量对象的不同,网络监测节点部署可以分为传统网络断层扫描监测节点部署和布尔网络断层扫描监测节点部署.

2.1.1 传统网络断层扫描监测节点部署

传统网络断层扫描技术主要针对网络性能指标的测量,即:基于监测节点间端到端的测量数据,推断网络内部链路性能指标.由于网络端到端测量数据的收集依赖于网络模型(包括网络拓扑、网络性能模型)和路由策略等的设定,当前的研究工作考虑了网络断层扫描在不同网络模型和路由策略下的监测节点部署问题.

就网络拓扑结构而言,通常可分为有向拓扑和无向拓扑两种类型:在有向网络拓扑中,两节点间链路(如v1v2)性能在其不同通信方向上(如v1→v2和v2→v1)具有不同的表现;相反,在无向网络拓扑中,两节点间链路性能在其不同通信方向上有相同的表现.对于有向网络拓扑的链路性能测量,Xia 等人[8]证明了除非网络中所有的节点都是监测节点,否则并不是所有链路的性能指标都是可测的.Gurewitz 等人[9]进一步证明了:当只使用环路形式的测量路径(measurement cycle)时,即使在网络中每个节点都是监测节点的情况下,仍然不能准确测量出所有链路的性能指标.对于无向网络拓扑的链路性能测量,文献[10-13]提出了基于探测包往返时间RTT(round-trip time)逐跳式(hop-by-hop)地测量链路时延的方法.该方法需要网络所有节点都运行了网际控制报文协议(ICMP).然而在有些实际的网络中,并不是所有的节点都允许使用ICMP 协议.此外,受因特网路由协议以及ICMP 协议的限制,探测包的往返路径可能是不对称的,从而难以保证其测量结果的准确性.由于逐跳测量方法在应用上存在的缺陷,很多工作研究了端到端(end-to-end)测量方法的可行性.

文献[11,12]研究了基于网络默认路由策略的链路性能测量问题,并证明了部署最少数量监测节点来获得网络中所有链路的性能指标是NP 难问题.文献[13]进一步证明了:即使在部分节点可以控制其本地路由策略的情况下,部署最少数量监测节点来获得网络中所有链路性能指标的问题仍是NP 难的.文献[14]研究了在给定网络路由策略时的链路性能测量问题,并提出了一个有效的近似计算方法,以基于网络节点的连接信息估算出一个自治系统内部链路的性能指标.Gopalan 等人[15]研究了当探测包路径可控的情况下,基于网络断层扫描技术的链路性能测量问题.Gopalan 等人[15]还在分析链路性能可测性(link identifiability)、网络拓扑和监测节点数量及位置三者之间关系的基础上,提出了一种最优的监测节点部署算法,并通过使用环路形式的测量路径进行探测包的发送和收集,从而计算出网络所有链路的性能指标.由于很多网络禁止兜圈子路由的方式,基于环路形式测量路径的测量方法在应用中难以实现.因此,基于非环路形式测量路径的链路性能识别问题受到了越来越多的关注.Ma 等人[16]推导了在仅仅使用非环路形式测量路径的情况下,网络中所有链路都可测的网络拓扑结构特征,并设计了一个最优的监测节点部署算法MMP(minimum monitor placement)[17].基于对拓扑连通性的划分,MMP 迭代地在每个连通分支上部署必要的监测节点,从而可以在线性时间内最小化监测节点的整体数量.这些早期工作为网络断层扫描技术的演变与改进提供了基础和指导.

现有的大多数监测节点部署算法旨在实现整个网络的可识别性,需要精确测量所有链路的性能指标.为了实现这一目标,即便最优的算法也可能需要部署数目不少的监测节点,如将ISP 网络中,64%的节点部署为监测节点[17].因此,部分网络可识别性(partial identifiability)问题受到了越来越多的关注.基于探测包可控路由的假设,文献[18]提出了一个有效的判别算法DIL-2M,以快速地识别出一个部署有两个监测节点的网络中所有可识别的链路.基于该算法,文献[19]提出了一个近似最优的监测节点部署算法GMMP,通过优化对给定数目监测节点的部署,从而最大化网络中可测链路的数量.另一方面,注意到有些实际应用往往只需要获取网络某些链路的性能,如处在网络关键位置上的链路.

为了提高网络断层扫描的灵活性,Dong 等人[20,21]提出了优先链路(preferential link)的概念,将网络中需要测量的链路指定为优先链路.为了降低优先链路测量的复杂度及减小监测节点的部署范围,Dong 等人首先提出了一种网络拓扑裁剪算法Scalpel[20].Scalpel 包含两个主要阶段:第1 个阶段,从原拓扑中裁掉不含优先链路的2-点连通分支(biconnected component)(如图3(a)所示);第2 个阶段,从第1 阶段裁剪后的图中裁掉一些边缘的3-点连通分支(triconnected component)和环分支(cycle).需要注意的是:在剩余的拓扑图中部署监测节点,可能无法达到在原拓扑图中部署的效果.为了不影响监测节点部署的性能,Scalpel 会从每一个被裁剪的分支中选取一个辅助节点(如图3(b)所示).在使用Scalpel 算法对原拓扑图G进行裁剪后,得到一个剩余的拓扑图Gt及辅助节点集合H.以图Gt和节点集合H为输入,Dong 等人进一步设计了最优监测节点部署算法OMA(optimal monitor assignment)[21],通过从图Gt和辅助节点集合H中选取最少数量的节点作为监测节点,实现对原网络拓扑G中所有优先链路的性能指标的测量.上述这些旨在实现部分网络可识别性的监测节点部署算法有助于服务提供商和管理员以较小的成本满足网络测量需求,提高了网络断层扫描算法的灵活性.

Fig.3 Illustrative example for the two stages of topology trimming algorithm图3 网络拓扑裁剪算法包含的两个阶段的说明示例

2.1.2 布尔网络断层扫描监测节点部署

当服务提供商和管理员想要测量的是网络状态参数时,要用到布尔形式的网络断层扫描技术.其中,网络内部运行状态可以用有限个零散数值表示,例如,用“0”表示链路通信正常,用“1”表示链路通信故障.

网络拥塞已成为网络传输性能和扩展性的重要影响因素,及时准确地定位网络拥塞,有助于网络性能调优和协议设计.基于网络中同时发生拥塞的链路数目较少的假设和给定的端到端路径测量信息,文献[22-24]使用压缩感知技术来识别因特网中发生拥塞的链路.在算法的实现中,通过引入一个用于判断链路通信正常与否的阈值,从而将链路性能小于阈值的数值转化为零.通过压缩感知技术,可以有效地恢复出链路性能大于阈值的数值,即识别网络中拥塞的链路.对于链路通信故障的定位问题,文献[25-28]利用概率统计方法从网络中找出一组最少数量的链路故障,从而能够完全解释测量的端到端的路径状态信息.文献[29,30]基于端到端的测量信息,使用贝叶斯方法计算网络中每一条链路发生故障的概率.

上述研究工作对网络允许的链路故障数目具有较严格的要求,在大规模网络场景中,难以保证其有效性.针对特定形式的通信模型(如客户-服务器),其网络拓扑往往相对固定.Duffield 等人[31]提出了一种简捷有效的链路故障定位算法,利用客户端与服务器之间路径的相似性,能够基于少数端到端测量信息,定位网络故障链路.进一步地,Ahuja 等人[32]形式化分析了网络拓扑结构、监测节点部署和链路故障识别三者的关系,并推导了在使用包含环路的测量路径时,链路故障的可识别性条件,并提出了一个最优监测节点部署算法,以准确定位出任意k条链路的通信故障.另一方面,有些工作关注于对网络节点通信故障的监测和定位.文献[33-35]研究了在不同探测包路由策略(任意可控路由、可控无环路由和不可控路由)下,网络节点通信故障的定位问题.具体地,文献[33,34]提出了有效的算法来计算对于给定的网络拓扑和监测节点部署,在一个特定节点集合中,最多可以同时发生故障的节点数目,以及给定允许发生故障的节点数目时,可以明确推算出状态的最大节点集合.针对采用客户-服务器通信模型的网络,He 等人[36]提出了有效的服务器节点部署算法,通过测量服务器节点与客户端之间的路径信息,从而最大化可定位节点故障的数量.该算法有利于拓展布尔网络断层扫描的适用范围.更为一般地,Bartolini 等人[37]推导了在给定测量路径数目、路由策略和网络拓扑形式(如树状和网状拓扑)等一般性信息的情况下,可以定位的发生通信故障节点的最大数量.该理论结果可以为网络拓扑设计和路由选择等操作提供参考和指导.

2.2 测量路径构造与选取

在网络断层扫描中,端到端测量数据的收集取决于使用的测量路径形式,不同的测量路径很可能产生不同的测量数据,从而可能得到不同的测量结果.近些年,很多工作从几何代数的角度研究了测量路径的构造和选取问题.当测量路径可以包含环路时,Gopalan 等人[38]提出了一种基于给定网络监测节点的线性无关(linearly independent)测量路径构造方法,并形式化证明了算法构造的测量路径是监测节点之间存在的一组最大数量的线性无关路径.该算法为基于环路测量路径的网络断层扫描技术(如最少监测节点部署[18])的实际应用奠定了基础.当测量路径不允许包含环路时,Wing 等人[39]推导了不同网络(有向和无向拓扑网络)中线性无关路径数目的界限值.

另一方面,Ma 等人[40]提出了一种具有多项式时间复杂度的无环测量路径构造算法STPC,基于网络中部署的监测节点构造出一组最大数量的线性无关且不含环路的测量路径,实现对所有链路性能的测量.该算法也为基于无环测量路径的网络断层扫描(如最少监测节点部署[17])的实际应用奠定了基础.为了简化监测节点间测量路径的构造,STPC 首先对网络监测节点进行合并操作.具体地,在网络拓扑中,STPC 引入一个虚拟监测节点,并分别用一条虚拟链路将原有的每个监测节点与虚拟监测节点连接起来.由于原拓扑链路(及路径)与新拓扑链路(及路径)之间存在着一一对应的关系,监测节点合并操作不会影响网络链路的可识别性,从而可以将原监测节点间无环测量路径的构造问题转换为虚拟监测节点上有环测量路径的构造问题.鉴于生成树不含回路的特性,STPC 接着在新拓扑图中以虚拟监测节点为根节点,构造了3 棵独立的生成树(如图4 所示).在每个网络节点上,通过这3 棵生成树的两两组合,可以得到3 条从该网络节点到虚拟监测节点的测量路径.最后,再将虚拟监测节点上的测量路径转换为实际监测节点间的测量路径.此外,将测量路径数据表示为线性方程组的形式后,生成树各节点上测量路径的嵌套结构使得对方程组的求解不需要采用传统高斯消元法的方式,即显示反转方程组系数矩阵.因此,STPC 能够确保在线性时间内计算出所有网络链路的性能指标.需要说明的是:STPC 在构造测量路径时需要网络中存在足够多的监测节点,以确保对所有链路性能指标的推算.这一前提条件可能会给网络管理员带来不小的测量成本,从而导致STPC 在实际应用时面临局限性.

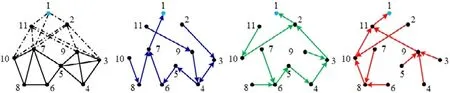
Fig.4 Illustrative example with a network topology and three independent spanning trees rooted at node 1图4 网络拓扑及其以节点1 为根节点的3 棵独立生成树的说明示例

测量路径的使用数量,很大程度上决定了探测包流量的大小[41-44].为降低测量负载对网络正常通信的影响,有些工作关注于对测量路径的选取及测量路径数目的减少.针对网络路径性能测量问题,Chen 等人[45]提出了一个在给定监测节点部署的测量路径选取方法,通过选取并测量一定数量线性无关的路径,从而可以计算出其他路径的性能指标.为了说明测量路径选取方法的可扩展性,Chen 等人[45]还推导了在任意规模的网络中,线性无关路径选取数目的界限值,并将该界限值表达成网络链路数目的线性函数形式.该结果为路径选取方法在大规模网络中的应用提供了坚实的理论依据.注意到网络路径大多都是线性相关的,文献[46,47]基于给定的一组路径测量信息,利用线性代数方法计算出其他未被测量的子路径上的性能指标.针对网络链路性能测量问题,Tang等人[48]基于网络拓扑和路径相关性信息设计了一种有效的路径选取方法,通过收集监测节点间少量路径的性能数据,推算出网络内部细粒度的链路性能界限值.

此外,针对网络中指定链路(即优先链路)的性能识别问题,基于实现网络部分可识别性的最优监测节点部署算法(如OMA[21]),Zheng 等人[49]设计了一种测量路径选取方法PathSelection.为了尽可能地减少测量路径的数目,PathSelection 首先从给定监测节点间的候选路径中确定出冗余的测量路径:可以被其他路径代替的路径以及对优先链路性能识别没有帮助的路径.然后,PathSelection 基于二分图模型(bipartite model)分析每一条优先链路识别与路径组合的关系,并迭代式地从二分图中找出一组可以识别所有优先链路且数目最少的路径作为最终使用的测量路径.在给定候选路径的情况下,PathSelection 虽然可以有效地减少测量路径数目,但在大规模网络中,要从给定的候选路径中找出所有可以识别优先链路性能的路径组合,并在二分图中确定一组数量最少的路径,可能会造成很大的时间开销.因此,如何从候选路径中快速地找到一组对链路性能识别最有帮助的测量路径,仍然是提高网络断层扫描有效性的一个关键问题.

2.3 测量数据分析与推断

在网络断层扫描技术中,监测节点按照一定规律(如周期性)或一定模式(如泊松分布)沿着测量路径发送探测数据包,将可以收集到一组(或一系列)端到端的测量数据.如何基于收集的测量数据准确地推断网络内部性能和状态对测量方法的有效性显得尤为重要.本节将简要介绍网络断层扫描常用的数据分析与推断方法.

根据网络性能参数特征,现有网络断层扫描的数据分析方法大致可以分为统计学习方法和代数计算方法.其中,统计学习方法针对的是性能参数在探测包收集过程中会变化的测量数据,而代数计算方法针对的是性能参数在探测包收集过程中相对稳定的测量数据.

基于统计学习的数据分析方法将路径性能和状态作为一个整体,通过端到端测量数据收集一个测量样本,并结合网络拓扑模型和网络性能模型推测出链路性能或通信状态的概率分布.其基本思想是:利用第1.2 节公式(1)或公式(2)所示模型构造一个分布函数f(c;x)来描述网络性能指标或通信状态特性的依赖关系.如果存在完整观测样本,就可以用参数估计的方法确定x.然而在网络断层扫描中,通常只能观测到部分样本数据,这使得数据推断变得比较复杂,需用统计学习的方法来估计那部分不确定的、观测不到的数据[50].常见的基于统计学习的测量数据分析过程如图5 所示.网络性能指标或通信状态对应于一个未知向量x,并在参数空间定义一个点,意味着已确定的推理估计目标.端到端测量数据c是观测空间的一些点,每个测量数据都在这个空间产生一个特有的点.函数f(c;x)表示这些空间之间连接的统计量,实际上是一组概率密度函数.通过这些观测数据,推理方法就能利用估计规则x′=g(c)来揭示测量对象x的值.目前,网络断层扫描主要的统计学习方法包含极大似然估计方法(maximum likelihood estimation,简称MLE)[51,52]、期望最大化(expectation maximization,简称EM)方法[53]和贝叶斯(Bayesian)估计方法[54]等.

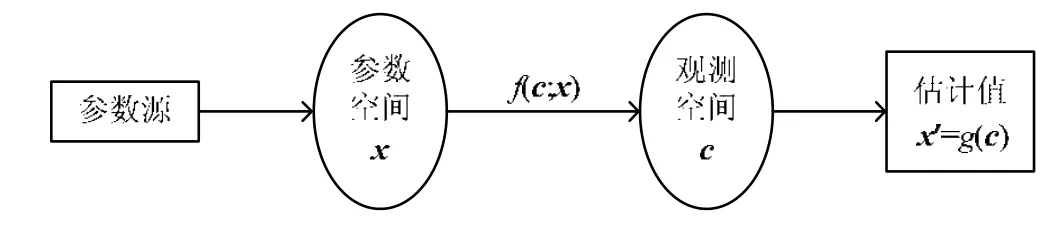
Fig.5 Statistical learning procedures for measurement data analysis图5 测量数据分析的统计学习过程

为测量所有链路性能的概率分布,在测量数据收集阶段,文献[55,56]利用多播的方式进行网络探测包的发送和接收,并提出了相应的多播树构造算法,证明了这种测量方式具有覆盖范围广、测量开销低的优势.在测量数据分析阶段,Chen 等人[57]应用傅里叶变换的技术对给定的路径性能数据做预处理后,结合广义矩估计的方法推断出单条链路性能参数的概率分布.注意到测量数据的质量可能影响到数据分析准确性,与传统给定路径测量信息来推断链路性能的方法不同的是,He 等人[58]基于费希尔信息(Fisher information)理论设计了一种探测包分配框架,用于计算在给定一组测量路径和给定探测包总数目的情况下,单条测量路径上探测包的发送数量,以使得收集到的路径测量信息可以最大化链路性能估计的准确率.同时,文献[58]将该探测包分配框架应用到链路时延测量和链路丢包率测量的实际问题中,基于框架收集到的路径测量信息和优化算法(D-最优化和A-最优化),准确地估算出了网络链路时延和丢包率的概率分布情况.针对网络链路通信故障的定位问题,文献[25-28]利用极大似然估计方法从网络中找出一组最少数目的链路故障,从而能够完全解释收集的端到端路径状态信息.文献[29,30]基于给定的端到端的测量数据,利用贝叶斯学习方法计算网络中每一条链路故障的概率.

基于代数计算的数据分析方法的基本思想是:将链路性能指标或通信状态刻画为一个未知常量,通过收集一组端到端路径的测量数据,结合网络拓扑模型和网络性能模型推测出链路的性能或状态.对于可累加的网络性能指标(如链路时延),一条端到端路径的性能指标等于路径上所有链路性能指标的总和.因此,代数计算方法可以将收集的路径测量数据表述成一个线性方程组的形式(如公式(1)所示),然后应用线性代数理论求解形式化的线性方程组,从而获得有唯一解(即唯一确定)的链路性能指标值.目前,网络断层扫描主要的代数计算方法有高斯消元法[18,19]、LU 分解法[22,23]、逆矩阵法[15,16]和增广矩阵法[49]等.基于高斯消元法的数据分析具有较好的通用性,在实际网络断层扫描中应用得较多,但其计算复杂度较大,在可扩展性方面有局限性.相反,基于LU 分解法和逆矩阵法的数据分析具有相对稳定的计算开销,但方法的使用需要满足一定的前提条件,如LU 分解法需方程组系数矩阵(公式(1)中的R)可分解成两个三角矩阵的乘积,逆矩阵法需方程组系数矩阵(第1.2 节公式(1)中的R)是满秩可逆的.基于增广矩阵的数据分析也具有较好的通用性,适用于需要测量不可识别(即无唯一解)的链路性能指标范围的场景.

3 应用挑战与关键技术

表1 总结了近些年网络断层扫描方法的相关研究成果.

概况地说,文献[11,12,15,17]从探测数据包路由策略的角度研究了在实现网络完全可识别性时的监测节点部署问题.其中,文献[11,12]基于网络默认路由协议的链路性能测量问题,并证明在基于网络默认路由(即不可控路由)策略下最少监测节点的部署是一个NP 难问题.随后,文献[15,17]分别从测量路径是否允许包含环路的角度提出了基于可控路由策略的监测节点部署理论和线性时间复杂度算法,从而为网络断层扫描技术的演变和改进奠定了基础.受网络测量成本的限制,文献[18-21]从实现网络部分可识别性的角度解决了监测节点的部署问题,确保可以用有限的成本满足服务提供商和网络管理员的测量需求,从而提高了网络断层扫描算法的灵活性.另一方面,网络内部运行状态也是网络测量的重要组成部分.文献[32-34,36]从探测数据包路由策略的角度研究了对特定数目链路(或节点)失效定位的监测节点部署问题,从而进一步拓展了网络断层扫描技术的适用范围.此外,文献[38,40,45,49]从测量对象和路由策略的角度研究了测量路径的构造和选取问题,并提出了相应的多项式时间复杂度算法.这些工作为网络断层扫描技术在各种形式网络中的实际应用提供了必要的基础.

从表1 中可以看出:当前已有许多网络断层扫描的理论和方法,但这些方法的设计在测量目标(或测量对象)、网络模型和测量成本等方面都有较为明确且严格的规定(或假设).这些规定假设虽然有利于方法的演变与验证,但也给方法的实际应用带来了局限性.

总体上,现有的网络断层扫描方法在性能测量粒度(及精度)、网络拓扑结构和网络通信模型这3 个核心方面都带有较强的假设和要求(见表2),这影响了网络断层扫描方法在实际应用中的有效性和通用性,甚至使得方法在有些网络场景中难以被使用.总体上,设计一个通用、高效及鲁棒的网络断层扫描方法面临以下3 项关键挑战:测量成本非常受限、网络拓扑的动态性以及网络通信的易失效性.近两年,越来越多的研究者开始关注已有网络断层扫描方法的局限性,并提出了相应理论和关键技术,以有效应对这些挑战.本节归纳了在应对上述挑战的一些代表性研究工作及其关键技术.

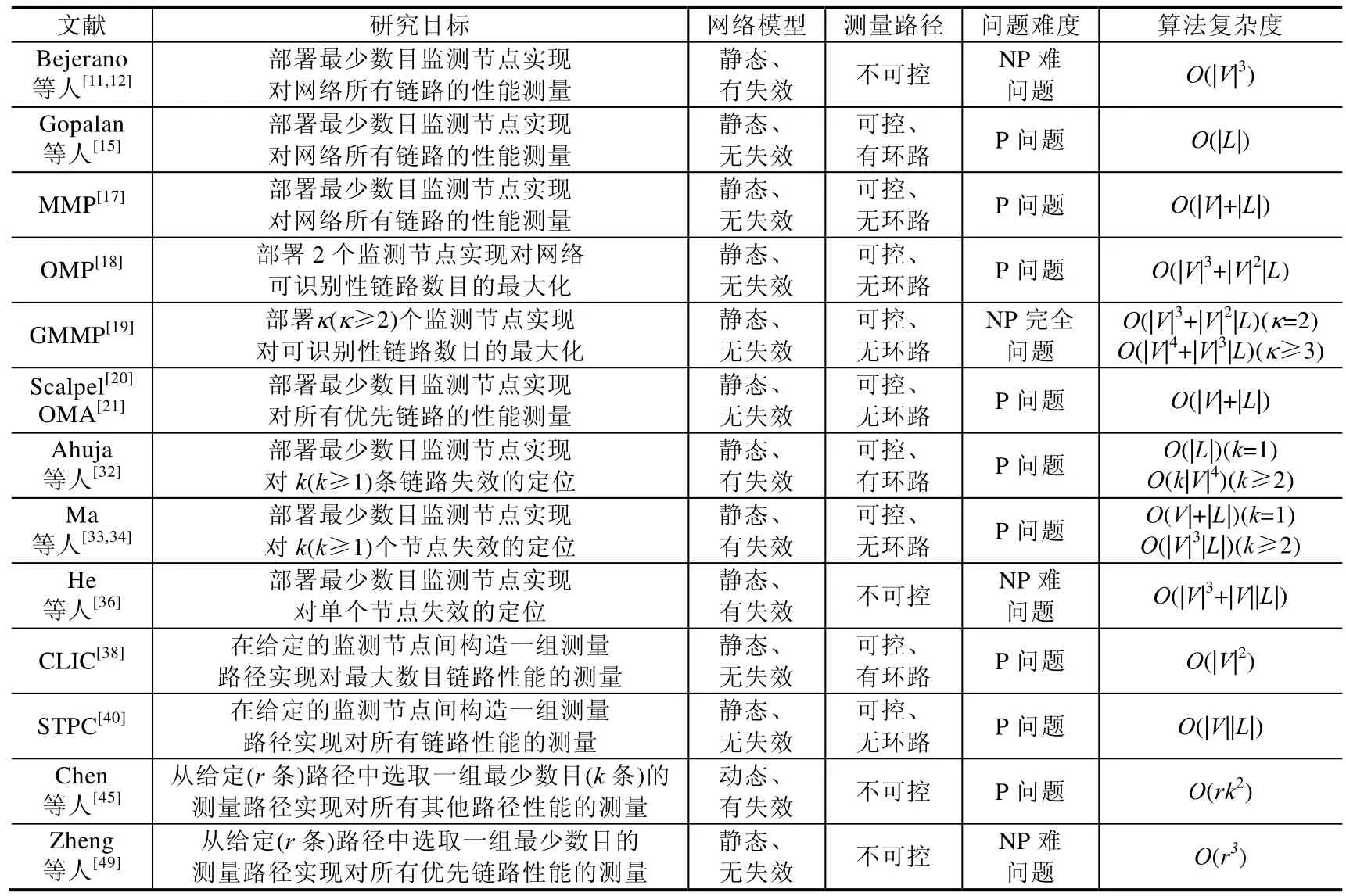
Table 1 Summary of network tomography methods表1 网络断层扫描方法总结

Table 2 Research status and key application challenges表2 现状及应用挑战

3.1 粒度可调网络断层扫描理论与技术

· 挑战

现有的网络断层扫描方法大多着重于实现对网络中所有链路性能指标确切值的测量,即测量粒度(及精度)单一且固定.这些方法存在两个主要缺陷:一是受网络拓扑和路由策略等的限制,测量网络所有链路性能的目标在很多应用场景中难以实现;二是测量链路性能指标的确切值往往会带来很大的开销,例如需要部署很多监测节点和发送大量探测数据包.为此,提出粒度(及精度)可调的网络断层扫描理论,并设计一种粒度(及精度)可调的网络断层扫描算法以有效平衡性能指标测量的精度与测量的开销,显得很有必要.

· 关键技术

在很多实际应用中,服务提供商与网络管理员通常关注的是网络内部性能是否符合与用户签订的服务水平协议(service level agreement,简称SLA)的要求,如网络丢包率是否处在SLA 规定的范围内[59].因此,链路性能指标的界限值将足以满足服务提供商与网络管理员的性能测量需求.鉴于此,Feng 等人[60]提出了一种有效的网络断层扫描方法,基于给定的监测节点和端到端路径测量数据,推算出网络中所有链路性能指标的界限值(包括性能上界和性能下界).简单地说,对于可识别的链路,其性能指标值可由与端到端测量数据对应的线性方程组唯一确定,所以可识别链路的界限值为同一个数,即,其性能界限的上界值等于下界值.对于不可识别的链路,已有网络断层扫描方法不会提供任何关于其性能指标的信息,而文献[60]的方法可以求解出其性能指标的界限值,且此时其上界值不等于下界值.

以图6 为例,网络中有两个节点(v2和v3)部署为了监测节点.假设网络中10 条链路(l1～l10)上的时延分别为{x1=7,x2=1,x3=5,x4=4,x5=6,x6=8,x7=13,x8=10,x9=3,x10=3}.需要说明的是,服务提供商与网络管理员一开始并不知道这些链路的时延,只有通过收集两个监测节点间端到端路径的时延数据,才能推算出单条链路的时延.因为网络中只有v2和v3为监测节点,基于链路可识别性条件[16,18],已有的网络断层扫描方法只能测量出链路l1和l6的时延,即只有链路l1和l6是可识别的.而对于网络中不可识别链路(l2～l5和l7～l10)的时延,已有的网络断层扫描方法不能提供任何信息.不同的是,通过使用文献[60]的网络断层扫描方法,网络管理员可以计算出不可识别链路上的时延范围:B(x2)=[0,7],B(x3)=[2,9],B(x4)=[3,10],B(x7)=[0,27],B(x8)=[0,27],B(x9)=[0,7],B(x10)=[0,7].

Fig.6 Illustrative example of network tomography for inferring performance metric bounds图6 测量性能指标界限值的网络断层扫描说明示例

通过对推算的链路性能指标界限值区间长度(bound interval length)赋上不同的约束,我们可以实现一种粒度可调的网络断层扫描.特别地,当要求链路性能指标界限值的区间长度为0 时(即要获得链路性能指标的确切值),文献[60]的方法转化为已有网络断层扫描方法.因此,文献[60]中的网络断层扫描方法是已有的网络断层扫描方法在测量目标上的一种推广演变.相比已有的旨在实现对网络所有链路性能指标确切值的方法,虽然文献[60]的网络断层扫描方法通过推算链路性能指标界限值的方式能够在很大程度上减少测量的开销,但推算网络所有链路性能指标界限值的复杂度与网络规模有很大关系,在大规模网络中容易造成指数级时间复杂度.

然而有些场景并不需要测量所有链路性能指标界限值,相反,服务提供商与网络管理员只需要获取一部分网络链路的性能指标界限值.比如在因特网中,被用户反映通信不正常的链路要比其他链路重要得多[61];在无线传感网中,位于基站(或网关)附近的链路由于承载的数据流量更大,通常成为限制整个网路系统性能的瓶颈[62].通过测量网络中这些优先链路(或目标链路)的性能指标界限值,可以进一步减少测量开销.更重要的是,还可以降低测量复杂度,有利于提高方法在大规模网络中的有效性.为此,我们研究了基于断层扫描的网络优先链路(preferential link 或interesting link)性能指标界限值的计算理论及测量技术[63].不同于文献[60]需推算网络所有链路性能指标界限值的要求,我们的方法关注于对服务提供商和网络管理员在网络中任意指定的一组优先链路性能指标界限值的高效测量.当指定网络所有链路为优先链路时,优先链路性能指标界限值的求解问题将转化为网络所有链路性能指标界限值的求解问题.因此,我们提出的网络断层扫描算法[63]相比文献[60]的网络断层扫描方法更加灵活和普适,具有更大的应用范围.下面我们简要介绍实现对优先链路性能测量粒度可调的网络断层扫描理论及技术[63]的核心思想.

考虑到服务提供商与网络管理员在不同阶段可能具有不同的测量需求,如:在网络运行阶段,关注的是如何通过已有监测节点有效地计算出网络中优先链路性能的界限值;在网络扩建或升级阶段,关注的是如何部署更多数目的监测节点以缩小计算的优先链路性能界限的距离.为此,我们在文献[63]中同时解决了以下两个关键问题.

· 优先链路性能指标界限值计算:在一个给定监测节点和优先链路的网络中,如何有效地推算出这些优先链路性能指标的最紧界限值,即最紧的上界值和最紧的下界值?

· 监测节点部署:在一个给定初始监测节点和优先链路的网络中,如何通过部署额外的监测节点以进一步缩小优先链路性能界限区间的长度(即上界值和下界值的差值)?

对于优先链路性能指标界限值的计算问题,基于对由端到端测量构造的线性方程组的可解情况及解空间分析,我们提出了网络优先链路性能指标界限值的计算理论,其中包含多种降低优先链路性能界限值计算复杂度的策略.由线性代数理论可知:方程组中不可解的变量可以分为自由变量和非自由变量两种类型,其中每个非自由变量可以表示成若干个自由变量的线性表达形式.然而,在一个没有唯一解的方差组中,通常有非常多种自由变量的组合方式.而每种自由变量组合方式都对应着一种方程组解的形式,在每种方程组解的形式中,都可以获得一个优先链路性能指标界限值.因此,在优先链路性能指标界限值的计算问题中,一个关键的挑战是如何确定出可以导致优先链路性能指标界限值最紧的一种自由变量组合方式.通过枚举所有自由变量组合方式并比较每种组合方式下优先链路性能指标界限值的方法,容易造成指数级的时间复杂度.注意到:在线性方程组中,对于一个特定变量(即目标变量),只有与其线性相关的变量才能影响到目标变量的求解.为此,在优先链路性能指标界限值的求解过程中,我们只选择与优先链路性能变量线性相关的变量作为自由变量,从而可以很大程度上缩小自由变量的选取范围,降低优先链路性能界限值计算的时间复杂度.

对于监测节点部署问题,基于对链路可识别性与优先链路性能界限值松紧程度关系的分析,我们设计了一个高效的监测节点部署算法NMPI[63].在网络原有监测节点的基础上,部署一个新的监测节点,从而最大程度上减小优先链路性能界限区间的长度.首先,NMPI 的设计基于一个重要的观察:在一个包含一组优先链路的网络中,对于新监测节点的部署,不可识别的优先链路性能指标界限区间长度只会受由新监测节点部署增加的可识别链路的影响,从而相同的链路可识别性也会造成相同的优先链路性能指标界限区间长度.因此,在监测节点部署过程中,对网络链路可识别性变化的分析成为了一个关键的问题.

由于网络可能部署有多个监测节点,而链路可识别性与单个监测节点之间存在着复杂的关系,为了简化监测节点部署对网络链路可识别性变化的分析,NMPI 对网络拓扑进行扩展操作.具体地,对于一个已有κ(κ≥2)个监测节点的网络G,引入两个虚拟监测节点(virtual monitor)1m′和m2′,同时,在实际监测节点(actual monitor)和虚拟监测节点间增加2κ条虚拟链路,在两个虚拟监测节点之间也增加一条虚拟链路(virtual link),将新生成的拓扑称为网络扩展图Gex(如图7 所示).由于原网络拓扑实际监测节点之间的端到端测量都可以转化为虚拟监测节点1m′和m2′之间的端到端测量,并且对于网络链路的测量,1m′和m2′之间的端到端测量相比实际监测节点之间的端到端测量不会提供额外的信息,所以原网络拓扑G的链路可识别性与扩展图Gex的链路可识别性是一样的,从而NMPI 可以关注于仅包含两个监测节点的扩展图Gex链路可识别性的变化.随后,NMPI 通过对新监测节点部署与网络扩展图Gex结构变化关系的分析,实现了新监测节点在网络扩展图Gex及原拓扑G中的最优部署.

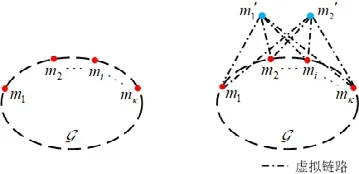
Fig.7 Illustration of topology extension operation图7 拓扑图扩展操作示例

此外,还有一些工作从测量对象的角度研究了粒度可调的网络断层扫描理论与技术.注意到在实际应用中,网络用户通常关心的是所用网络服务的性能,例如从客户端向服务器发送请求到客户端收到回应的时延,Yang等人[64]解决了网络任意节点间端到端通信路径性能的测量问题,并提出了一种最优的监测节点部署算法MPIP,通过收集监测节点间一组端到端测量数据,以实现对任意指定路径(即优先路径,interested path)性能指标的推算.为便于网络监测节点的部署,文献[64]首先研究了基于断层扫描的网络优先路径性能的可识别性理论,形式化表述了拓扑结构、监测节点和路径可识别性这三者的关系,并解决了给定监测节点部署时,网络可识别路径的判断问题.基于网络路径可识别性条件,MPIP 将网络拓扑划分成多个2-点连通和3-点连通分支,根据各连通分支中优先路径特性,迭代地在各连通分支中部署必要的监测节点,从而用最少的监测节点实现对所有优先路径性能指标的计算.需要说明的是,上述这些粒度(及精度)可调网络断层扫描方法[60,63,64]在实现过程中,使用的是不含环路的端到端测量路径,这有利于提高方法在实际网络中的可用性.

3.2 动态拓扑网络断层扫描理论与技术

· 挑战

随着物联网、软件定义网络等新型网络形态与网络技术的兴起,动态的网络路由拓扑越来越成为这些新型网络的重要特点[65].例如在典型的物联网场景中,动态路由协议(如RPL[66]、低功耗蓝牙mesh 网络路由等)被广泛用于应对无线信道、节点位置等的动态性,从而使得网络路由拓扑不断发生变化.而在软件定义数据中心网络中,流量分割(traffic splitting)[67]技术及重路由(re-routing)[68]技术被广泛用于负载均衡,使得同一个数据流的数据包可以通过不同的路由到达接收端,从而导致了网络路由拓扑的动态性.现有网络断层扫描技术[16,17,19,21]的典型工作模式是基于已知的静态网络拓扑,部署一定数量的监测节点并获取监测节点间探测包的测量数据,然后结合网络拓扑信息建立关于内部运行状态的方程组,最后通过求解方程组完成网络测量的目标.然而,当网络路由拓扑动态变化时,某一时刻存在的路由路径下一时刻可能就不存在了,而某一时刻必要的监测节点在另一时刻可能是冗余的.因此,如何在动态拓扑的条件下进行精确、高效的网络断层扫描,是一个非常重要的问题.

· 关键技术

在动态拓扑网络中,由于链路(或节点)的动态性,在某一个时刻的拓扑中部署的监测节点可能并不适用于另一个时刻拓扑中链路的性能测量.一种简捷的动态拓扑网络测量方法是:当网络拓扑变化后,利用基于静态拓扑的网络断层扫描方法[21,25]在新生成的网络拓扑中重新部署一遍监测节点.这种应急式(reactively)的部署方法虽然可以实现对多个网络拓扑的性能测量,但频繁地更换监测节点部署位置一方面给网络管理员带来了不小的成本开销,另一方面也不利于网络测量任务的平稳进行.因此,在网络拓扑变化前,先验式(proactively)地实现对链路性能的测量显得尤为重要.

He 等人[69]首次研究了动态拓扑网络链路性能的测量问题,并提出了一种有效的网络断层扫描方法,通过在网络规划初期,一次性部署一定数目的监测节点,以实现对网络所有可能拓扑中所有链路的性能测量.然而,要想获得动态拓扑网络中所有链路的性能,即使最优的监测节点部署算法也可能需要使用大量监测节点(如网络90%以上的节点需为监测节点[69]),这将会造成很大的测量成本.另一方面,很多时候,服务提供商与网络管理员只关注网络某些链路的性能指标,例如处在网络关键位置上的链路性能指标.通过测量网络中优先链路的性能指标,在满足应用需求的同时,也可以很大程度上降低测量成本.为此,我们研究了面向动态拓扑的优先链路测量理论及技术,其中包含多种高效及鲁棒的网络断层扫描方法[70],通过在动态拓扑网络中部署尽量少的监测节点,以实现对所有可能拓扑中优先链路的性能测量.不同于文献[69]计算网络所有链路性能指标的要求,我们的方法旨在用更少的成本计算出网络中任意指定的一组优先链路的性能指标.当指定网络所有链路为优先链路时,对优先链路性能指标的测量问题将转化为对网络所有链路性能指标的测量问题.因此,我们提出的网络断层扫描方法[70]是文献[69]中网络断层扫描方法的泛化,具有更好的测量灵活性.下面我们简要介绍实现对动态拓扑网络中优先链路性能有效测量的网络断层扫描方法[70]的核心思想.

网络断层扫描方法的设计需要网络拓扑信息作为基础,而尽早地获取动态网络在各个时刻的拓扑信息,有助于监测节点的部署.因此,我们首先研究了基于网络拓扑预测的优先链路可识别性理论,从而为动态拓扑网络监测节点的部署提供指导.由于动态网络拓扑结构的周期性和可预测性(例如行车路线和运行时刻固定的公交车网络、睡眠/工作模式周期性交替的低功耗传感网),可以利用拓扑时空相关性及过去一段时间的网络拓扑,预测未来一段时间内的网络拓扑.另一方面,我们设计了一种通用及简洁的时变网络模型来刻画动态拓扑网络的在各个时刻的拓扑结构.简单地说,我们将网络测量周期(或生命周期)划分成若干个等长的时隙,然后将网络在各个时隙上的拓扑结构用如下序列的形式来表述:

其中Gt表示网络在第t个时隙上的拓扑.

图8 所示为一个具有4 个节点(A～D)的动态拓扑网络在3 个不同时隙上的拓扑结构.

Fig.8 Illustrative example for topologies in different slots of a dynamic network图8 动态网络在不同时隙的拓扑结构示例

确定了动态网络在各个不同时刻上的拓扑后,我们提出了动态拓扑网络中优先链路的可识别性理论,解决如何一次性部署尽量少的监测节点以保证对网络所有拓扑中优先链路的性能测量问题.具体地,考虑到监测节点可能部署位置的数目将随着网络规模呈指数增长,我们分析优先链路的可识别性与监测节点部署位置的关系,通过裁剪掉对优先链路性能测量无影响的部分节点,缩小监测节点部署的选择范围,从而加快网络断层扫描的实现过程.

随后,我们解决了动态拓扑网络的监测节点部署问题.注意到现有工作[20,21]已实现对静态拓扑网络中优先链路性能测量的监测节点部署算法,存在一种比较直接的动态拓扑网络监测节点部署方式:在网络拓扑序列(如公式(4)所示)中依次应用静态拓扑的监测节点部署算法,获得网络各时隙上的监测节点部署,再将所有时隙上监测节点部署的并集作为动态拓扑网络最终的监测节点部署结果.这种监测节点部署方式虽然可以保证各网络拓扑中优先链路的可识别性,但可能会部署上冗余的监测节点,给服务提供商与网络管理员造成了不必要的开销.以图9 所示的动态网络为例,在该网络中,节点v2和节点v6在时隙1 的拓扑G1中连通,在时隙2 的拓扑G2中断开.在网络两个时隙的拓扑中,假设网络管理员只需要测量链路v1v4和链路v1v5的性能.在拓扑G1中,为了获得这两条优先链路的性能,基于文献[21]中的部署算法,我们可以从{v2,v3,v6,v7,v8}中任选两个节点部署监测节点,所以M1={v6,v7}为一种可行的部署方式;而在拓扑G2中,选v2和v3作为监测节点,可以测量出优先链路v1v4和v1v5的性能,即M2={v2,v3}.因此,最终我们在该动态网络中部署的监测节点为M1∪M2={v2,v3,v6,v7},即需要4个监测节点.由于M2本身也适用于拓扑G1中优先链路性能的测量,这种对不同时隙网络拓扑单独处理的方式部署了两个冗余的监测节点,即v6和v7.

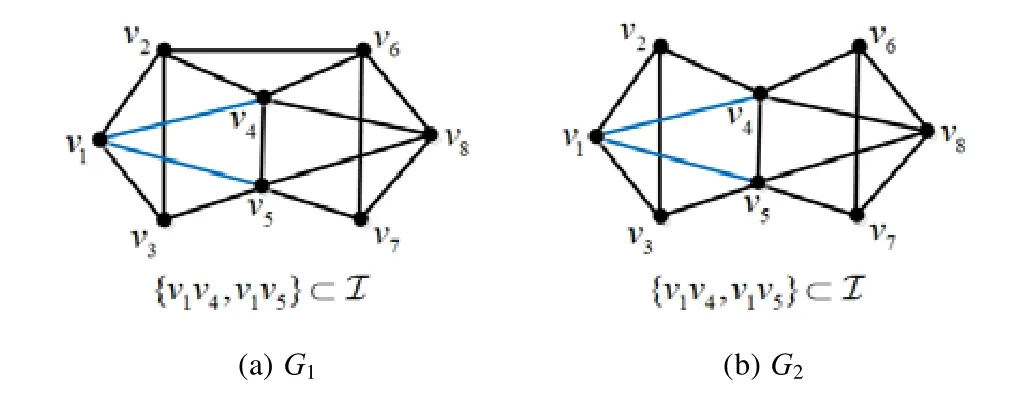
Fig.9 Illustrative example for monitoring node placement in a dynamic network图9 动态拓扑网络中监测节点的部署示例

为此,在监测节点的部署过程中,我们综合考虑了动态网络各时隙拓扑中监测节点的部署需求,并用如下约束条件的方式刻画单个拓扑的监测节点部署:

其中,Si为网络节点集合,表示在单个拓扑中可供选择的监测节点部署位置;ni表示从Si中至少需要选择的节点数目.

得到动态网络每个拓扑中监测节点部署的约束条件后,我们将监测节点的部署问题规划成最小碰撞集问题(minimum hitting set problem,简称min-HSP).利用最优化理论,可以从整个网络中选取出最少数目的节点作为监测节点,以满足各约束条件.相应地,我们能够用最少的监测节点来保证动态网络中优先链路的可识别性.

3.3 通信失效网络断层扫描理论与技术

· 挑战

现有的很多关于网络断层扫描技术的研究工作尝试回答网络拓扑与链路可识别性具有何种关系这一问题[15,16,18,19],想要了解对于给定拓扑,如何部署监测节点测量出网络中所有(或部分)链路的性能指标.但是这些工作假设在测量过程中网络通信都是完全可靠的,未考虑到网络通信失效的情况.然而在实际应用中,通信失效在多种形式的网络中是较为常见的[71],如链路故障、节点变更和信道冲突等.因此,提出通信失效网络断层扫描理论并设计鲁棒的网络断层扫描算法,以保障在网络发生通信失效时测量任务的顺利进行,也是一个亟待解决的问题.

· 关键技术

对于特定的监测节点部署,当发生通信失效(如链路失效)时,其能观测到的路径是不同的,包含失效链路的路径将不能被观测到,从而可能使原来可识别的链路变得不可识别.以图10 中链路l6的测量为例,在该网络拓扑中,节点v2被部署为监测节点,通过测量3 条起止于v2的路径性能数据(p1:l2l1l6,p2:l3l4l6,p3:l2l1l4l3),可以推算出链路l6的性能(如时延).用xi表示链路li的性能,ci表示路径pi的性能,则3 条测量路径的性能与链路性能可以用图10 中的线性方程组关联起来,其中每条测量路径分别对应于方程组中的一个线性方程.通过求解该线性方程组,可以计算出链路l6的性能指标值c6=(c1+c2-c3)/2,即链路l6在监测节点v2下是可识别的.然而,当链路l2发生通信失效时,测量路径p1:l2l1l6和p3:l2l1l4l3由于包含l2将变得不可用,方程组将只包含方程②的信息,此时链路l6将变得不可识别.因此,现有的监测节点部署方法无法有效应对链路失效对网络性能测量的影响.值得注意的是,有些链路在网络中任意其他k条链路失效的情况下仍然是可识别的.例如图10 中l3在网络其他任意1 条链路失效时,仍可以通过其他测量路径的端到端数据推算出其性能指标值.如果我们能够了解怎样的拓扑特征可以使得链路具有这种性质,将有助于指导监测节点的部署以及网络拓扑的设计,实现鲁棒的网络测量.此外,不同的监测节点部署也可能导致不同的链路可识别性.如果将监测节点部署在v5,那么无论有无链路失效发生,网络中所有的链路都将变得不可识别.

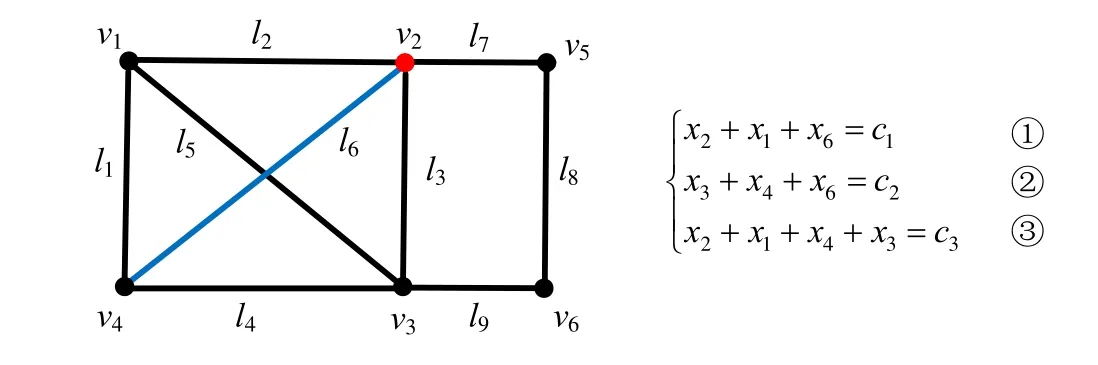
?Fig.10 Example to illustrate the impact of link failures on network tomography图10 链路失效对网络断层扫描的影响示例

针对这种情况,我们在文献[72,73]中研究了网络失效下的链路可识别性理论,包含一条链路在其他任意k(k≥0)条链路失效情况下仍然可以识别的充分必要条件,并根据链路可识别性理论设计了监测节点的部署算法,解决了如何在有链路失效的情况下部署监测节点,以进行鲁棒的网络断层扫描.首先,为了量化链路失效对链路性能识别性的影响,我们提出了k-可识别性(k-identifiability)的概念.

· 一条链路(非失效链路)被称为k-可识别的(k-identifiable),当且仅当该链路在网络中任意k条链路失效时仍是可识别的;

· 一个网络被称为k-可识别的,当且仅当网络中所有链路都是k-可识别的.

需要说明的是:当k=0 时,k-可识别表示当网络无通信失效时链路是可识别的(即已有网络断层扫描方法的可识别性),此时也记为0-可识别.k-可识别的链路一定是(k-1)可识别的,k越大,表示该链路对于其他链路失效的容忍度越大.可以看出:如果我们能得到链路k-可识别和网络拓扑结构的关系,将帮助网络管理者有效地部署监测节点,以使得网络中k-可识别的链路数目尽可能多.同时,这也能帮助网络设计者了解如何设计网络能够使得网络链路为k-可识别的,实现鲁棒的网络断层扫描[74].

具体地,我们在文献[72,73]中通过回答以下两个密切相关的问题,来帮助网络设计者和网络管理员达到上述目标.

· 对于一个给定监测节点部署的网络,哪些链路是k-可识别的?

· 对于一个给定监测节点数目的网络,如何部署这些监测节点,以使网络中k-可识别的链路数目最大?

针对k-可识别性链路的判断问题,对于一个有n条链路的网络来说,网络中k条链路失效的场景有种,通过枚举每一种失效场景去判断一条链路是否是k-可识别的是不可行的.为此,我们选择通过对网络拓扑进行适当划分来研究链路k-可识别性在监测节点部署和拓扑结构方面的判定理论.具体地,我们给出并证明了在不考虑链路失效(k=0)时,链路可识别(0-可识别)的充分必要条件(见表3).在此基础上,进一步给出并证明了在考虑链路失效(k>0)时,链路可识别(k-可识别)的充分必要条件(见表3).基于这些证明的链路k-可识别性条件,我们可以基于网络拓扑结构和监测节点部署位置,在多项式时间内判断出一条链路是否是k-可识别的,而不需要枚举所有链路失效情况,显著降低了k-可识别性链路判定的复杂度.

Table 3 Necessary and sufficient conditions for k-identifiability of links[72,73]表3 链路k-可识别性的充要条件[72,73]

对于特定数目(κ个)监测节点的部署问题,一种比较直接的方法是:根据链路k可识别性的判定条件,在网络中枚举所有监测节点部署位置,并比较每种部署情形下k可识别链路的数目,最后输出使得k可识别链路数目最大的监测节点部署方式.考虑到网络中存在种可能的监测节点部署方式,这种枚举方法的复杂度将随着网络规模呈指数级增长,不具有可扩展性.相反,我们在文献[72,73]中形式化地表述了特定数目监测节点的部署问题,并说明了这是一个NP 完全问题.随后,我们提出了一种贪心算法MPK 来解决这个问题.MPK 的核心思想是:因为在网络的(k+3)-边连通分支中部署一个监测节点必然能使其中的链路都是k-可识别的(见表3),所以MPK首先在(网络的每个(k+3)-边连通分支中随机地选择一个节点,构成监测节点部署的候选集合.接着,MPK 枚举了第1 个监测节点部署的所有位置,这是因为第1 个监测节点不同的部署往往会给算法最后的结果带来较大的影响.当第1 个监测节点的位置选定后,MPK 将一个一个地从候选集合中选定剩余的κ-1 个监测节点.每次选择中,MPK 都将选择使得当前k-可识别的链路数目最多的位置部署监测节点.需要说明的是:通过此算法,我们可以逐步增加监测节点的数目,直到网络中所有链路都为k-可识别时,此时的监测节点部署为开销最小的部署方式.

虽然文献[72,73]中的监测节点部署能够确保链路在网络失效情况下的k-可识别性,但k-可识别性概念针对的是网络随机(或任意的)链路失效场景,同时,监测节点部署过程也将网络链路失效刻画为不可预测的.这种悲观式链路失效刻画方式容易生成次优的监测节点部署结果,即部署冗余的监测节点.然而在很多网络场景中,基于网络通信模式特征和现有拓扑预测模型[75,76],服务提供商和网络管理员能够一定程度上预测出未来一段时间内的网络失效情况,即存在一部分可预测的网络失效.为此,我们在文献[77]中进一步提出了一种能够同时应对可预测和不可预测链路失效的网络断层扫描方法,基于对网络链路失效的预测,在保证链路k-可识别性的同时,进一步减少监测节点部署数量,降低测量的成本.为了满足网络管理员在测量成本与实现复杂性上的不同需求,我们还提出了多种监测节点部署算法[77](如简单取并集法、增量部署法和综合部署法等),以达到监测节点部署成本和时间复杂度之间的平衡.

4 总结和未来工作

与传统网络内部测量方法不同,网络断层扫描作为一种新型的网络外部测量方法,能够在没有中间节点协作的条件下,根据网络边缘的测量数据推测出网络内部性能指标和运行状态,从而实现与网络组成及协议无关的网络测量.本文首先给出了网络断层扫描的基本概念和形式化表述,并指出了影响网络断层扫描性能的3 个重要因素:监测节点部署、测量路径构建和测量数据分析.接着,对近年来学术界在这3 个影响因素方面的代表性研究工作进行了归纳分析.其中,针对网络状态识别问题,本文还介绍了布尔形式网络断层扫描在监测节点部署方面的研究成果.随后,本文分析了已有网络断层扫描工作在实际应用中的核心缺陷,并总结了针对这些核心缺陷近年来提出的最新理论及算法.

目前,网络断层扫描的发展和应用仍然是网络测量领域研究的热点,存在大量开放性问题有待更加深入的研究.以下列举出几个未来可能的发展方向.

(1) 通用有效的网络断层扫描性能模型.当前,学术界已经提出了很多网络断层扫描算法,如MMP[16],OMA[21],MPIP[64]和MAPLink[70]等.这些网络断层扫描算法依赖于不同的网络模型,具有不同的数据收集和数据分析方式.此外,这些算法在测量开销、测量精度(及粒度)、实现复杂度等方面也有不同的表现.因此,设计一个通用有效的网络断层扫描性能模型,以准确刻画测量可用资源(带宽资源、计算资源、存储资源)与测量算法性能之间的关系,将有助于服务提供商与网络管理员在相同条件下(如给定测量开销)对比不同方法的优劣,从而便于根据当前网络的特性和测量的需求选择最合适的网络断层扫描算法,实现测量开销和测量精度之间的平衡.

(2) 更鲁棒的测量算法和分析方法.网络断层扫描技术的应用,离不开测量数据的收集和分析.测量数据收集的质量,直接影响测量结果的性能.由于采用间接测量的方式,网络断层扫描测量数据的收集容易受到许多实际因素的影响,如链路拥塞状况、节点存储状况和网络路由等.而其中任意一个因素的变化,将很可能使得传统网络断层扫描方法变得不可用.虽然近几年已有部分工作[69,70,72,77]考虑了鲁棒断层扫描问题,但大多针对的是特定因素的影响,如节点位置更新和链路失效等.如何考虑更加全面及实际的网络设置,根据其特征进一步扩展和改进网络断层扫描算法,仍然是一个需要思考的问题.此外,受环境干扰、网络流量等影响,监测节点上收集的测量数据可能带有一些误差.虽然已有统计学习方法可以在一定程度上规避测量数据的噪声,但其往往具有较大的复杂度,难以保证测量的实时性.因此,未来需要在目前研究基础上探索更加鲁棒的网络测量算法和更加通用的数据分析方法.

(3) 网络测量信息挖掘和智能分析.针对大规模网络的性能测量,是近年来网络测量领域的研究热点之一[74].目前,实现对大规模网络的性能评估,需要长时间持续不断地测量才能获取全面而准确的数据.因此,网络断层扫描还要面对大规模测量可能带来的海量数据和数据时效性的问题[3].另外,通过对网络断层扫描测量信息的跟踪与统计分析,有助于服务提供商与网络管理员迅速、直观地判断网络性能的变化趋势,并及时定位网络瓶颈和故障的位置,在网络性能恶化之前予以解决,保证网络服务的可用性和有效性.因此,实现网络测量信息的智能分析和预测将有助于网络的管理及优化,具有广泛的研究意义和应用价值.可以预见:一种高效、鲁棒及智能的网络断层扫描技术将可以提升我们了解网络运行机理的能力,支撑网络性能的持续优化.