利用灰色残差GM(1,1)-Markov模型预测水工混凝土的劣化
2021-03-06康春涛王忠慧杨轶群
康春涛,贡 力, ,王忠慧,杨轶群,王 鸿
(1. 兰州交通大学 土木工程学院,甘肃 兰州 730070;2. 兰州交通大学 调水工程及输水安全研究所,甘肃 兰州730070)
我国西北干寒地区具有冬长暑短、雨热同季、日照时间长、年降水少、蒸发量、昼夜温差大和年季温差较大的高寒半干旱气候特点。据水利部资料统计,我国西北地区混凝土水工建筑物70%的破坏受损都与地区的严寒气候有关[1-2]。大多数水工混凝土建筑物出现剥蚀甚至脱落现象。因此,对水工混凝土建筑物劣化预测模型的研究,对于水工建筑物的结构安全和寿命维护具有重要的意义。
目前,对于混凝土劣化预测的方式有很多种。肖前慧等[3]提出了冻融循环下混凝土抗压强度指数衰减规律预测模型和寿命预测模型;冯忠居等[4]基于灰色系统理论,建立了不同工况下混凝土相对动弹性模量GM(1,1)预测模型;邬晓光等[5]利用可拓评价模型实现对混凝土梁式桥耐久性的预测;胡宸瑞[6]采用Wiener分布模型对其在不同环境因素下的服役寿命进行预测;马俊军等[7]在Fick第二定律的基础上,建立了考虑氯离子随机扩散效应的元胞自动机模型等。刘荣桂等[8-10]诸多专家在理论上对混凝土耐久性的预测提出了创新方法。近年来,众多专家在灰色理论的基础上,提出了残差模型和马尔科夫(Markov)理论相结合的预测方法[11-12]。张克中等[13]在灰色残差基础上提出马尔科夫残差修正灰色模型,并将其应用于公路网规划中运输量的预测;陈佳琪等[14]采用传统GM(1,1)模型和改进后的残差修正GM(1,1)模型分别对房屋建筑面积统计数据进行预测;杜永强等[15]以最大延伸率作为性能变化表征参数,根据老化反应速率常数随温度的变化关系,建立了马尔科夫灰色残差GM(1,1)模型,对常温条件下推进剂的老化反应速率常数进行了预测。通过结合灰色残差和马尔科夫模型,不仅让两个模型能体现各自的优点,而且能弥补数据信息波动性大的不足,能更好地提高预测模型精度[16]。目前,针对混凝土劣化的预测模型,大多数集中在公路、桥梁及房建等混凝土建筑物,对于西北干寒地区水工建筑物的研究较少;另外,基于灰色残差GM(1,1)-Markov模型在水工混凝土劣化预测方面的研究较少。
本文将灰色残差GM(1,1)的马尔科夫模型应用于水工混凝土建筑物劣化试验预测,通过实验室方法来验证预测模型的适用性。首先对混凝土试件进行耐久性劣化试验,以质量和抗压强度的原始值作为初始数据,通过一系列数据处理,得到灰色GM(1,1)模型和残差GM(1,1)模型。然后利用马尔科夫过程的符号修正,对灰色残差GM(1,1)模型进行马尔科夫修正,以此来预估混凝土试件在盐冻作用下的寿命。
1 利用GM(1,1)模型预测强度或质量损失
1.1 灰色GM(1,1)模型
参考郭鹏等[17-18]的理论,本文对灰色GM(1,1)模型的建立过程是将混凝土劣化的质量损失和抗压强度损失过程累加生成数列模型,再将数列模型进行处理,最终得到预测值。用X(0)(k)表示劣化试验寿命的原始数据序列,设原始数据为:

对X(0)(k)做一次累加生成算法,生成一阶累加生成数列:

由式(2),计算得到x(1)(k)的紧邻均值系列Z(1),Z(1)={z(1)(2), z(1)(3),···, z(1)(n)},其中:

构建微分方程dx(1)/dt+αx(1)=β,其中,参数α、β可由下式得到:

求解上述微分方程,得到如下GM(1,1)模型:

用如下累减公式还原,即可计算出预测值:
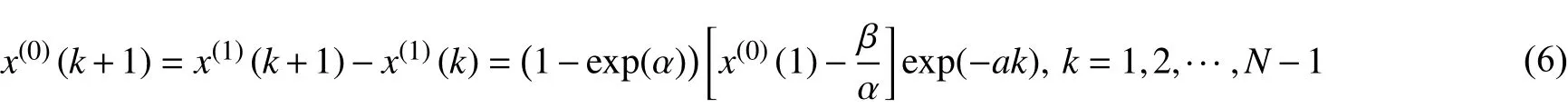
式中:x(0)(k+1)为第(k+1)项的预测值;x(0)(1)为原始数据序列的首项;α、β分别为GM(1,1)模型的系数和常数项,由最小二乘法(回归)求得。
1.2 灰色残差GM(1,1)模型
为了修正预测值与混凝土劣化试验初始值结果的差异,建立残差序列ε1(0),ε1(0)={ε1(0)(2), ε1(0)(3),···,ε1(0)(n)},其中:


对得到的ε(0)按式(2)~(6)的步骤建立灰色GM(1,1)模型,可得:

其中,参数aε、bε按照式(4)求解,则残差修正值为:

用得到的残差修正值 修正还原值x(0),得到:

1.3 马尔科夫过程的符号修正
由于预测模型仅是对原始数据的规律总结,可能会导致原始数据与预测数据的相对误差较大,因而有必要对模型进行改进。故本文将灰色残差GM(1,1)和马尔科夫模型应用于水工混凝土劣化试验的预测中,以提高预测模型的精度[19]。
统计残差序列的频数,规定状态:残差正值为状态1,残差负值为状态2。根据其状态的正负,得到状态转移概率矩阵如下:

把残差从状态i转移到状态j的概率记为Pij,例如,P12代表从状态1转移到状态2的概率,Pij≥0,且可由下式确定:

式中:sij为状态i转移到状态j的次数;si为状态i出现的次数。
其余计算过程参考文献[18],此处不再赘述。
由下式计算相对误差:

2 试验数据处理及寿命预估
2.1 数据来源与试验设计
参考《普通混凝土长期性能和耐久性能试验方法标准》,试验采用慢冻法。采用100 mm×100 mm×100 mm立方体标准试件,试件设计抗冻标号为D200,试件规格强度为C30的试件,共120块,其中水泥型号为甘肃省祁连山水泥集团股份有限公司生产的P·O 32.5水泥。另外,考虑细骨料和粗骨料中的含水量(分别为2.4%和1.0%),混凝土材料组成见表1。

表 1 混凝土材料组成Tab. 1 Concrete mix proportion
试件成型后拆模,在养护箱中养护至28 d龄期。试件分为4个部分,每部分为30块。参考普通混凝土长期性能和耐久性能试验方法标准,在试验前4 d把试件从养护地点取出,分别置于清水及质量浓度为3、5和7 g/L的Na2SO4溶液中进行浸泡,对应试件分类编号为:1-0、1-3、1-5和1-7。
将经过浸泡的试件按照其分类,进行盐冻试验,每25次小循环之后,清理试件上的碎渣,并及时称量,用轴心抗压试验仪进行抗压试验,计算质量损失率及抗压强度损失率。当质量损失率达到5%,或抗压强度损失率达到25%或达到盐冻试验次数(根据设计抗冻标号,其次数为200~250次),可认定为达到破坏条件,结束试验。
2.2 数据处理
限于篇幅,本文抽取清水和3 g/L硫酸钠溶液侵蚀的试件质量和抗压强度损失统计数据进行计算。水工混凝土在盐冻作用下,试件质量和抗压强度随着次数的提高而减小,具体数据见表2。

表 2 盐冻作用下混凝土试件质量和抗压强度原始统计值Tab. 2 Original statistical values of the quality and pressure strength of concrete specimens under the action of salt freezing
以清水浸泡过的混凝土试件为例,计算原始质量的灰色模拟值和残差模拟值如下。本文0~125次盐冻试验的质量作为原始值,预测150~200次的数据。原始数据及预测结果见表3。

表 3 混凝土试件质量的模拟结果Tab. 3 Simulation results of the quality of concrete specimens
由表3可知,基于马尔科夫的GM(1,1)模型的模拟结果中,经过清水浸泡和盐冻试验的混凝土试件质量的最大误差为0.29%,最小误差为0.01%,平均误差为0.10%;经过3 g/L硫酸钠溶液浸泡和盐冻试验的混凝土试件质量的最大误差为0.20%,最小误差为0.000 9%,平均误差为0.03%。
由模拟结果可见,灰色GM(1,1)模型的质量模拟结果误差较大(1-0和1-3的最大相对误差分别为0.37%和0.21%),但是灰色残差GM(1,1)模型经过残差修正之后,相对误差明显降低(1-0和1-3的最大相对误差分别为0.33%和0.06%)。
相应地,可计算出经过清水浸泡和盐冻试验的混凝土试件抗压强度模拟结果见表4。

表 4 混凝土试件抗压强度的模拟结果Tab. 4 Simulation results of the pressure strength of concrete test pieces
由表4可知,基于马尔科夫的GM(1,1)模型的模拟结果中,经过清水浸泡和盐冻试验的混凝土试件抗压强度的最大误差为1.16%,最小误差为0.05%,平均误差为0.51%;经过3 g/L硫酸钠溶液浸泡和盐冻试验的混凝土试件抗压强度的最大误差为0.33%,最小误差为0.05%,平均误差为0.165%。
在不同浓度下,灰色GM(1,1)模型的抗压强度模拟得出:1-0和1-3系列最大相对误差分别为2.53%和1.30%。经过灰色残差GM(1,1)模型修正之后,1-0和1-3系列最大相对误差分别降为1.16 %和0.33%。相对误差的变化,可以证明经过修正的灰色残差GM(1,1)模型对抗压强度的模拟效果要比灰色GM(1,1)模型好。
通过以上计算分析得出:相对于灰色GM(1,1)模型,残差修正GM(1,1)模型能更好地贴合原始数据的质量损失和抗压强度损失过程。所以,此模型可用于现有的数据预测,并对现有数据的规律得出预测模型经验公式。
2.3 符号修正
由于第225次盐冻试验的试件抗压强度已失效,故本文应用灰色残差GM(1,1)模型,仅对清水及浓度为3 g/L的硫酸钠溶液侵蚀的混凝土试件的150、175、200次盐冻试验的质量和抗压强度进行预测,并确定残差修正值的符号。
根据表3混凝土试件质量的模拟结果,对150次盐冻试验的质量预测如下:
根据马尔科夫过程的符号修正,残差由正数向正数转移的次数是1,正值出现的次数是2,因此,其概率P11=1/2,同理可得P12=1/2、P21=1/3、P22=2/3。由此可得马尔科夫状态转移矩阵P为:

将盐冻试验125次的混凝土质量作为初始状态,由表3知其残差值为负,因而初始向量s(0)=(0,1)。由式(13)得到第150次盐冻试验的结果为:

即第150次盐冻试验的混凝土质量残差修正值为正的概率为1/3,为负的概率为2/3,因此取正号。预测150次盐冻试验的质量见表5。以150次盐冻试验的质量残差修正值为初始值,同理可得出175、200次质量的预测值。同理可得3 g/L硫酸钠溶液侵蚀的混凝土试件的质量(表5)。
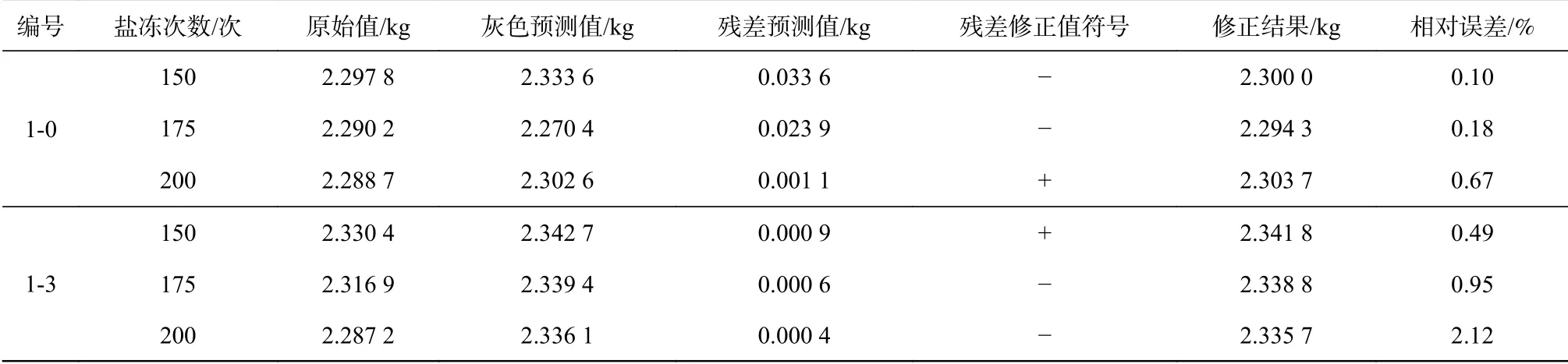
表 5 混凝土试件质量预测结果Tab. 5 Prediction results for the quality of concrete test pieces
由表5可知,通过Markov模型的符号修正,在不同硫酸钠溶液浓度下水工混凝土试件150~200次盐冻试验的质量原始值与预测值,最大误差为2.12%,最小误差为0.10%,且相对误差随着盐冻试验次数的增加而变大。
同理,可得清水和3%硫酸钠溶液浸泡侵蚀的混凝土试件的抗压强度预测值,见表6。

表 6 混凝土试件抗压强度预测结果Tab. 6 Prediction results for the strength of resistance of concrete test pieces
由表6可知,混凝土试件在盐冻试验下,抗压强度预测值的最大误差为1.91%,最小误差为0.13%。由于马尔克夫符号修正预测序列较长,相对误差略有偏大,但总体来看属于正常误差范围,符合预测模型对于误差的要求。这表明该模型对于混凝土劣化过程预测具有较好的适用性。
对比质量和抗压强度的初始值、灰色GM(1,1)模型计算值、灰色残差GM(1,1)模型计算值、马尔科夫过程符号修正计算值见图1。如图1所示,由于质量的单位基数较小,使得质量预测的相对误差较为明显。
根据最初的灰色GM(1,1)模型的预测,并对此模型进行残差修正,得到灰色残差GM(1,1)模型。通过与初始数据的对比,可以发现灰色残差GM(1,1)模型精度有了明显提高。最后,利用马尔科夫过程的符号修正,对混凝土试件150~200次盐冻试验的试件质量损失和抗压强度损失进行预测,使得预测结果更符合实际情况,为混凝土水工建筑物的劣化预测指标提供理论支撑和技术保障。

图 1 数据修正与模型预测对比Fig. 1 Data correction and model prediction comparison chart
3 结 语
(1)以灰色GM(1,1)模型为基础,经过数据累加生成数列模型,依次得到灰色GM(1,1)预测模型和灰色残差GM(1,1)预测模型。通过残差值的频数统计得到状态转移矩阵,并对预测数据的符号进行修正,得到了灰色残差GM(1,1)-Markov模型。
(2)借助灰色残差GM(1,1)-Markov模型对经过盐冻试验的水工混凝土试件的质量和抗压强度进行预测,结果表明:质量和抗压强度的预测值与原始值相比误差较小,最大误差为2.12%,最小误差仅为0.13%。验证了在一定的预测范围内,该模型对混凝土劣化的质量和抗压强度损失具有很好的预测效果。
