海域航空重力快速构建区域大地水准面
2021-03-05王晨阳骆遥熊盛青刘诗华刘祖鉴
王晨阳, 骆遥, 熊盛青, 刘诗华, 刘祖鉴
1 中国地质大学(北京) 地球物理与信息技术学院, 北京 100083 2 中国自然资源航空物探遥感中心, 北京 100083 3 国防科技大学智能科学学院, 长沙 410073
0 引言
航空重力以航空器为测量平台,综合利用重力传感器、惯性导航系统、全球卫星定位系统等测定空中重力加速度(孙中苗等,2004;熊盛青等,2010).航空重力测量始于20世纪 80年代(张永明等,2006),随着导航技术以及高精度重力传感器技术的应用,近年来航空重力测量技术获得了突破性进展,测量精度达1×10-5~2×10-5m·s-2(熊盛青,2009),空间分辨率3~5 km.航空重力测量不受作业区域限制,能够快速获得均匀分布的高精度重力场观测资料,同船测、地面重力测量相比作业效率更高.海域航空重力测量可以弥补卫星测高数据在近海及海陆交互带、浮冰区等目标区域观测精度较低的问题(Brozena et al.,1990;Hwang et al.,2006),是海洋地球物理探测的重要手段之一.
大地水准面是与全球无潮平均海平面重合并延伸至大陆内部的重力等位面,是空间高程的基准面(Grafarend,1994;吴晓平,2006;魏子卿,2009;林淼等,2012),其形状反映了地球内部物质密度结构、应力场、地球旋转和洋流等信息(Vanichek and Christou,1994).大地水准面与地球重力场模型关系密切,现代大地水准面的确定以地球重力场的位理论为基础(张利明和李斐,2005),近年来通过航空重力测量精化大地水准面成为研究热点(蒋涛,2013;孙中苗等,2014;刘金钊等,2020).目前,我国已在管辖海域开展了大规模的航空重力勘探,为海域基础地质调查和油气资源调查提供了重要基础性资料(李文勇等,2010;张玄杰等,2016).利用已有航空重力数据构建管辖海域大地水准面,对拓展航空重力勘探应用方向具有现实意义.本文针对海域航空重力勘探实际,利用高精度向下延拓等关键技术,实现了一种快速高效构建海域大地水准面的方法,可为确定海域大地水准面提供技术支撑.
1 大地水准面建模
大地水准面与重力场密切相关,Brun公式(Heiskanen and Moritz,1967)给出了二者的直接联系,即大地水准面起伏可以由重力扰动位除以正常重力值确定.大地水准面建模的关键在于将实测航空重力异常转换为重力扰动位.
1.1 位场转换近似
大地测量中通常通过斯托克斯积分计算水准面(许厚泽,2006),即
(1)
其中:N是地心纬度为φ、地心经度为λ处的水准面起伏,R是地球半径,S(ψ)是斯托克斯积分核,Δg是球面积分区域σ对应的重力异常.如果该积分区域有限,可将球面近似为平面,即斯托克斯积分将近似为
(2)
其中:N是(x,y)处的水准面起伏,γ是正常重力值,Δg是平面积分区域s上相应的重力异常.该积分是卷积形式,利用傅里叶变换可将其写成频率域形式,即
(3)
其中,F[·]表示傅里叶变换,u、v是Δg傅里叶变换后x、y方向对应的波数,F[·]-1表示傅里叶变换的逆变换.因此,大地水准面起伏N可以通过公式(3)表达的频率域位场转换确定.
对于航空重力勘探,测量高度通常高于积分面,需要将测量的重力异常向下延拓至积分面.陆域航空重力测量观测面多是随地形起伏的曲面,难以严格应用位场转换条件进行向下延拓.海域航空重力通常测量的是距海平面或椭球面等高的重力异常,具备平面位场转换的适应条件,可直接向下延拓至积分面,即
(4)
其中:Δgh是实测航空重力异常(空间重力异常),h>0是测量高度,u、v是Δgh傅里叶变换后x、y方向对应的波数.因此,海域水准面起伏可利用航空重力资料通过重力勘探中位场转换方法近似计算,即对航空重力进行向下延拓,再对其进行垂向积分并除以正常重力值获得.由于位场转换要求待转换的位场为平面网格数据,利用公式(3)和公式(4)确定大地水准面在一定范围内忽略了地球曲率影响,但频率域位场转换算法处理效率非常高,可用于航空重力测量成果快速构建局部海域大地水准面.
1.2 高精度向下延拓技术
海域航空重力采用固定飞行高度测量,可直接将航空重力异常从平均飞行高度(椭球高)向下延拓至椭球面.向下延拓可以从数学上拉近观测平面与场源间的距离,改善信噪比,增强地质信息,但重力异常向下延拓却是经典的不适定问题(Blakely et al.,1996;曾华霖,2005;黄谟涛等,2018),采用公式(4)进行向下延拓将强烈的表现出对数据高频部分的振荡,向下延拓后的数据通常无法直接使用.由于还需对向下延拓的重力异常进行垂向积分,也可将频率域向下延拓算子同垂向积分算子连乘进行位场转换,该算子为
(5)
由于公式(5)的位场转换算子隐含垂向积分操作,相比直接向下延拓,一定程度上会减少对异常高频部分放大的程度,略显稳定.Cooper(2004)曾应用类似(5)式的位场转换算子进行处理,再进行空间域求导得到相对稳定的向下延拓结果.尽管公式(5)表示的位场转换较直接向下延拓更稳定,但直接对实测航空重力数据进行处理,仍将出现高频振荡,特别是航测高度较高的情况下.目前,国内海域航空重力勘探测量高度为800 m或1000 m,通常的向下延拓处理仍难以获得椭球面上稳定的异常数据.
位场转换还存在假值填补与数据扩边问题.快速傅里叶变换(FFT)对网格数据的行、列数有一定要求,通常要求为2的自然数次幂.网格化后的航空重力异常数据一般不满足该条件,需要对网格数据进行扩边,扩边效果直接影响后续处理的精度,Nagy和Fury(1990)曾就数据扩边对重力异常转换大地水准面精度的影响进行过讨论.实际航空重力异常资料还因测网设计、偏离航线、测线掐线等限制,网格化后某些区域无法形成相应的内插数据进而存在网格格点空白,处理时要求对空白区进行填补,这也将影响处理的精度.为了解决上述问题并提高处理精度,本文采用位场向下延拓的最小曲率方法对航空重力异常进行向下延拓(骆遥和吴美平,2016).具体采用如下迭代形式进行向下延拓,即
(6)
其中:Δgk表示第k次迭代后的航空重力向下延拓结果;η是权重系数;downcα(h)表示正则化参数为α的最小曲率向下延拓算子,h>0是向下延拓距离;upc(h)是延拓距离为h的向上延拓算子.上述处理解决了实际非规则航空重力测量中空白区及网格扩边问题,提升了航空重力勘探向下延拓处理的实用性,可高精度的获取下延平面上观测异常对应的位函数.
1.3 移去与恢复
上述向下延拓获得的异常即为扩边后的下延重力异常,直接对其积分即可得到相应的位函数.对异常进行积分时,零频u=v=0处算子存在奇异,通常将奇异时算子设为0(Lourenco et al., 1973),加之存在积分误差,位函数的长波长部分无法准确确定.因此,位场转换所确定的位函数是相对的,而扰动位的基准直接关系到水准面,必须确定其起算基准.为解决该问题,这里采用移去-恢复法的思想(黄志洲等,2004),用EGM2008等重力场模型确定低频重力场,其最终确定的大地水准面包括局部航空重力异常计算部分和重力场模型计算部分,即
N=NΔg+NGM,
(7)
其中:N是大地水准面起伏,NΔg是局部航空重力异常确定的水准面起伏,NGM是重力场模型确定的大地水准面.
2 模拟计算
为了检验构建大地水准面的位场转换方法,我们采用EMG2008模型(阶次2159)模拟航空重力数据和大地水准面,检验方法的精度.按1∶1000000标准图幅范围,计算我国香港幅(114°E—120°E,20°N—24°N)海域高1 km(大地高)航空重力测量数据,图1给出了模拟的海域航空重力测量数据,其中网格距为1 km,对应陆域范围内的数据均设为空白.航空重力测量通过引入重力基点可以获取绝对重力场,图1a的海域航空重力场数据为EGM2008计算的绝对重力场.我们将EGM96模型(阶次360)对应的绝对重力场移去,图1b给出了移去后的航空重力异常.采用1.2节向下延拓方法将图1b重力异常向下延拓1 km归算至椭球面,并对延拓后的重力异常进行积分换算成位函数,计算相应的水准面起伏(图2a).图2b给出了通过(7)式最终确定的大地水准面,其中模型水准面部分采用EGM96.我们将计算的大地水准面同EGM2008模型进行比较,二者最大相差37 cm,标准差10.27 cm, EGM2008模型全球平均精度为13 cm(Pavlis et al.,2012),构建的水准面精度与此相当,说明该方法具有较高的计算精度.
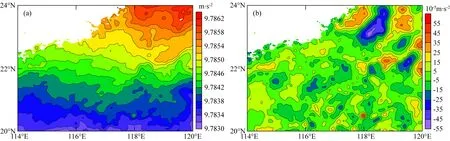
图1 模拟的海域航空重力场(a)及移去后航空重力异常(b)Fig.1 The simulated airborne gravity field of sea area (a) and airborne gravity anomaly after removal (b)
3 实际航空重力资料计算
为检验位场转换方法实际构建海域大地水准面效果,我们采用航空重力实测资料进行处理.使用的数据为美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)所属的国家大地测量局(National Geodetic Survey,NGS)在波多黎各附近加勒比海海域实测航空重力数据.该航空重力测量是美国构建下一代垂直基准GRAV-D计划的一部分,并利用地面绝对重力测量点将空中重力异常数据进行了归算,最终航空重力测量成果以测量高度上的绝对重力场表达.图3给出了实测的航空重力测线及航空重力数据.采用塞斯纳奖状喷气飞机(Cessna Citation II )搭载美国Micro-g LaCoste公司的TAGS航空重力系统进行测量,设计的飞行高度为10.668 km,实际平均飞行高度为11226.11 m,测线间距为10 km,切割线间距约40 km.图3b航空重力数据的网格距为2.0 km(航空地球物理测量中网格距通常为测线间距的1/5~1/4).由于测线边缘不整齐,网格化后的格网数据南北部边缘存在数据空白.此外,区内两条测线上部分存在问题的数据已被掐去,造成网格化后的格网数据开“天窗”.图3反映了实际航空重力测量的典型特征,目前一些通过模拟航空重力数据精化水准面的研究中通常回避了上述数据特征,直接用EGM2008等重力场模型来模拟不含数据空白的规则矩形格网数据.根据1.3节的技术路线,利用EGM2008重力场模型(阶次2159)计算重力场的模型部分,并将其从实测数据中移去,图4a给出了移去后的重力异常,异常幅度为-8.3×10-5~7.87×10-5m·s-2.利用1.2节的方法将图4a的重力异常向下延拓,图4b给出了下延后的重力异常.向下延拓的距离为11226.11 m(实测平均椭球高),图4b可视为图4a归算至WGS-84椭球面上的重力异常.图4b经向上延拓至原测量面并同图4a比较,误差的标准差为0.26×10-5m·s-2,99%的网格点误差幅度不高于0.91×10-5m·s-2,说明向下延拓具有很高的数值精度.
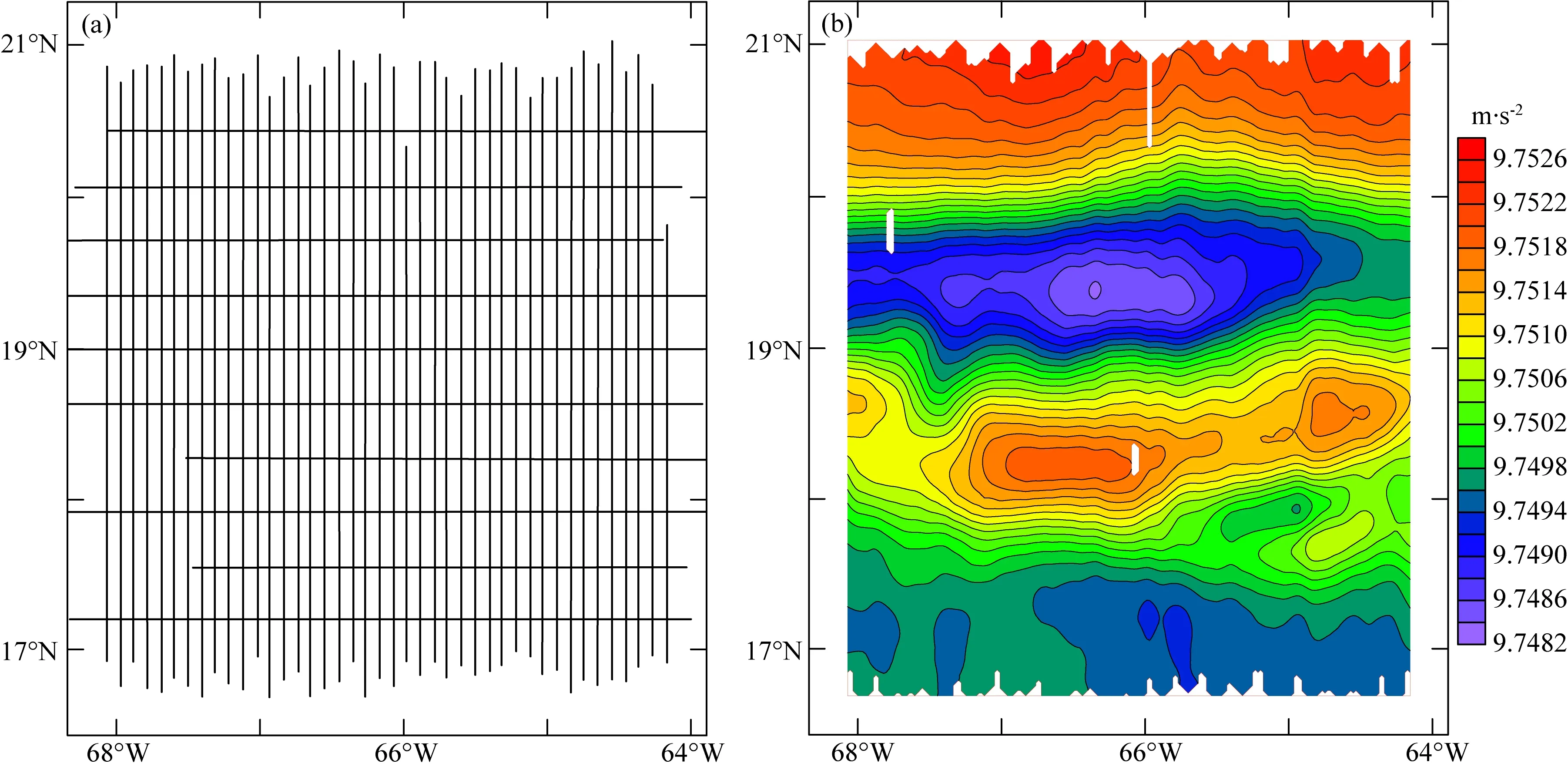
图3 航空重力测线(a)及实测航空重力数据(b)Fig.3 Airborne gravity survey lines (a) and airborne gravity field data (b)

图4 航空重力异常(a)及下延至WGS-84椭球面上的异常(b)Fig.4 Airborne gravity anomaly (a) and its downward continuation result on the WGS-84 ellipsoid (b)
将图4b归算至WGS-84椭球面上的重力异常转化为相应的扰动重力位,图5a给出了相应的计算结果.扰动位精度直接影响大地水准面精度,为了消除积分的水平误差,将图5a的位函数反算为航空重力异常,并将其同图4a进行比较,图5b给出了位函数转换重力异常的误差.图5b给出的误差分布表明计算的位具有很高的精度,误差呈正态分布,误差幅度约2×10-5m·s-2量级,标准差为0.27×10-5m·s-2,基本同向下延拓误差的标准差0.26×10-5m·s-2相当.尽管误差的标准差很小,但误差的平均值为2.11×10-5m·s-2,表明零频处理中存在相应系统差,需进一步消除.我们将图5a的位函数求导,转换为重力异常同图4b进行比较,二者误差的标准差为5×10-12m·s-2,几乎为0,误差的平均值为2.11×10-5m·s-2,这表明零频置0的处理中忽略了2.11×10-5m·s-2的重力场直流分量.因此,零频处理中引起的系统误差造成图5a扰动位比实际要大,其忽略的重力场常量在垂向的积分近似为0.2369 m2·s-2(即2.11×10-5m·s-2×11226.11 m).
补偿图5a资料中0.2369 m2·s-2的系统差后,计算剩余异常所引起水准面起伏,图6a给出了图4a对应的水准面起伏,其幅度最大约30 cm.最终,利用公式(7)将图6a同EGM2008水准面融合,图6b给出了该测区最终确定的大地水准面.
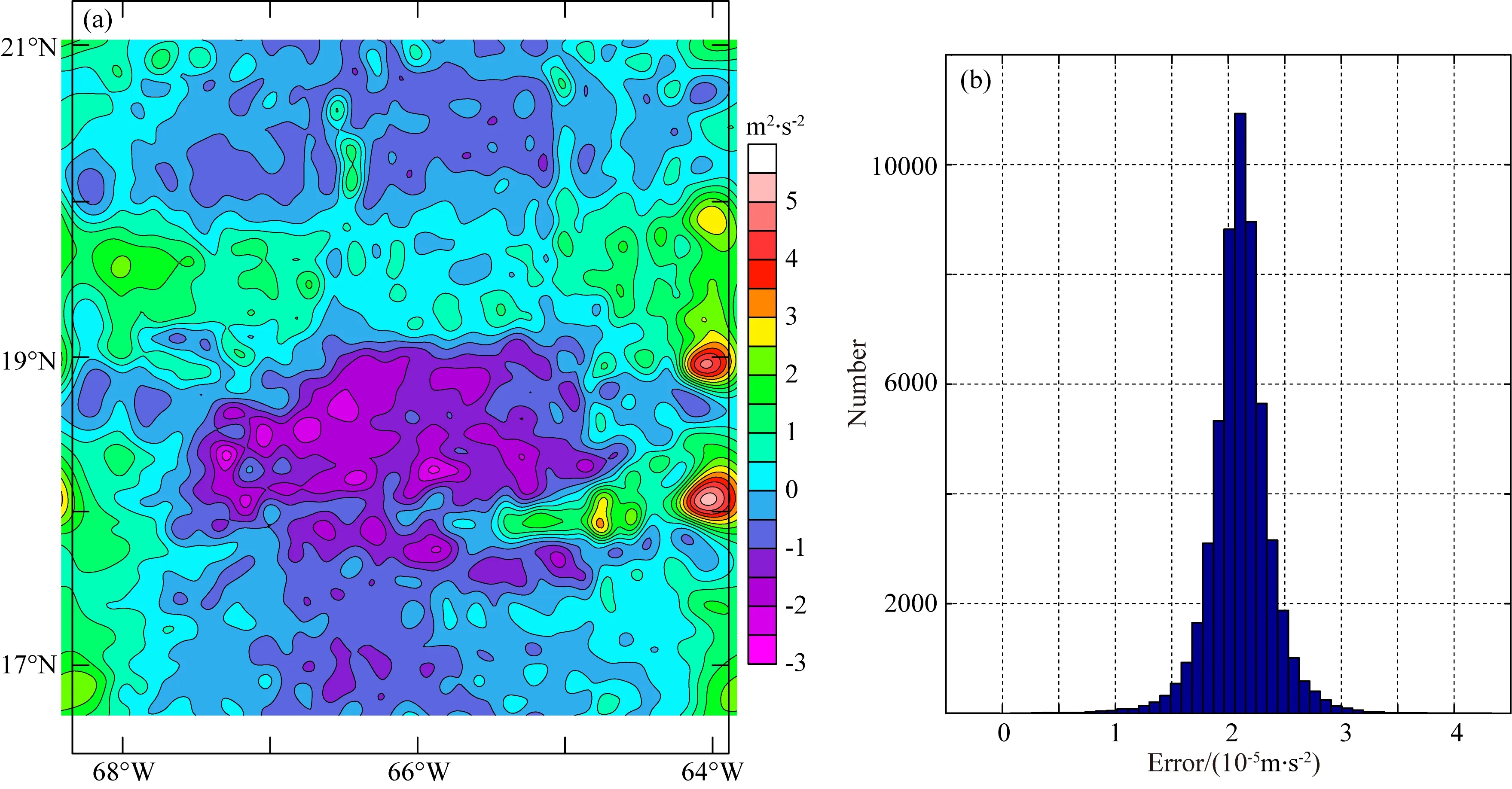
图5 由剩余异常计算的位函数(a)及误差(b)Fig.5 Gravity potential field calculated by residual anomaly (a) and error (b)
图6表明该区的大地水准面起伏在-70.84 m至-40.61 m之间,精化大地水准面起伏不超过38 cm,从位场转化误差分析其精度约为2×10-5m·s-2,与测区航空重力实测精度1.85×10-5m·s-2基本相当,这是从位场转换方法本身的精度去评价构建大地水准面的精度.为了进一步检验方法的精度,这里采用测区内美属维尔京群岛上的21个GPS/水准点进行检验(由于向下延拓存在过场源问题,该检验方法仅为近似评估),图7给出了GPS/水准点分布.将GPS/水准点的水准面同EGM2008模型大地水准面及通过航空重力测量精化的大地水准面进行比较,图8给出各点位的水准面及大地水准面对比情况.GPS/水准点给出的水准面同EGM2008大地水准面模型及本文给出的大地水准面趋势均较为一致,但GPS/水准测量采用了VIVD09垂直基准,同大地水准面间存在水平差.图8表明VIVD09的参考水准要高出EGM2008大地水准面2.5 m的量级,如果忽略二者间的水平差,以GPS/水准测量为标准,EGM2008模型的大地水准面精度可用二者差值的标准差代表,其精度为10.85 cm.本文给出的大地水准面同GPS/水准测量也存在类似水平差,以GPS/水准测量为标准,二者差值的标准差为6.36 cm,较EGM2008大地水准面的精度提高了约4 cm.上述检验使用的GPS/水准点均位于岛屿处,检验中假设了向下延拓过场源时将参考椭球外部的质量压缩至椭球面上,存在一定的近似.为此,我们采用美国xGEOID18B水准面模型进行了检验.图6b给出的水准面同xGEOID18B相比,最大相差18.9 cm,二者差值的标准差为5.08 cm,可见本文的海域航空重力测量快速精化大地水准面方法具有较高的精度.
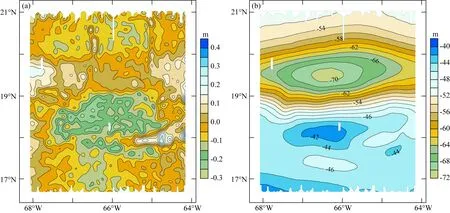
图6 大地水准面修正量(a)及修正后大地水准面(b)Fig.6 Correction of geoid (a) and final geoid determined (b)
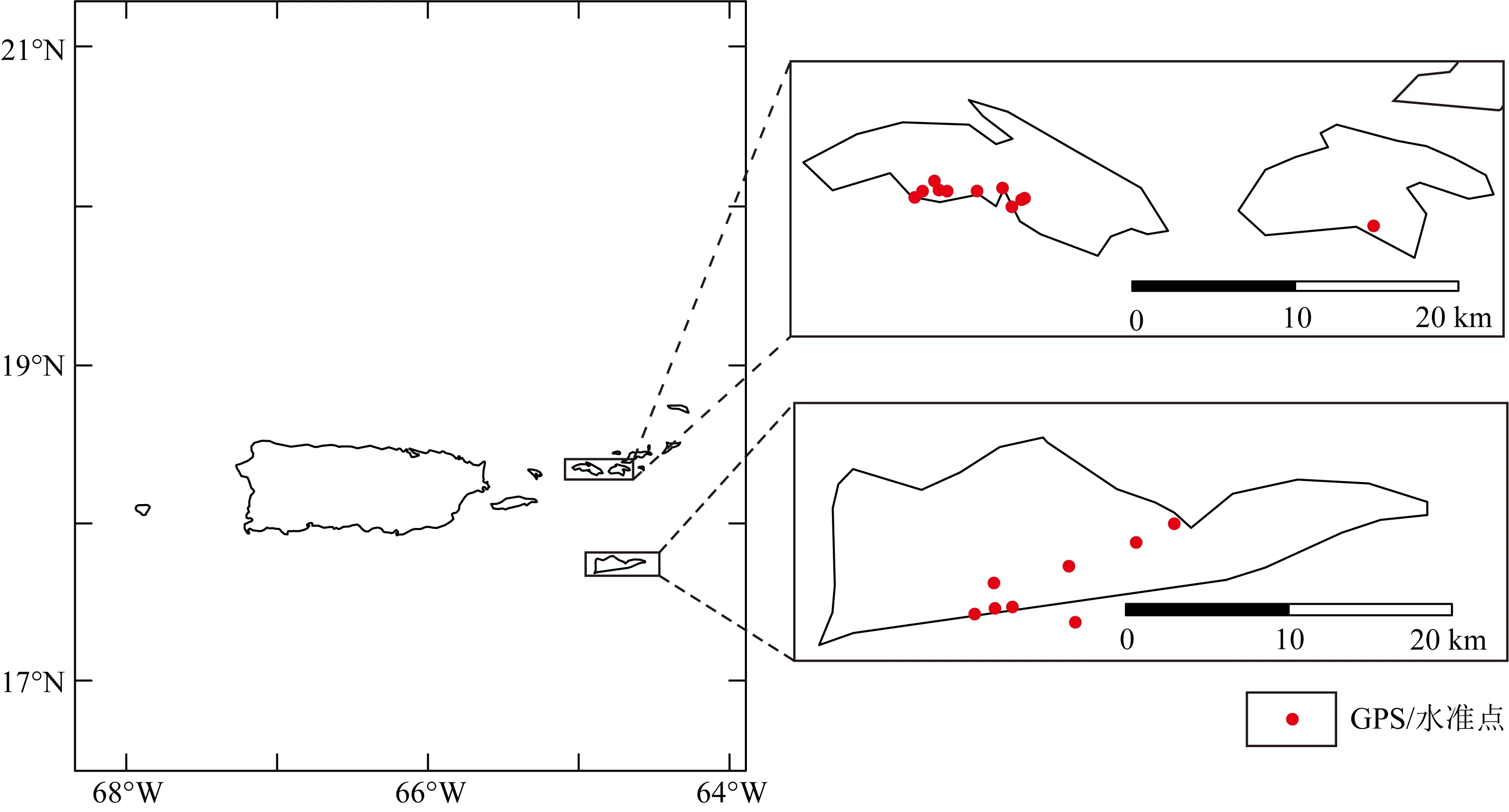
图7 GPS/水准点分布Fig.7 GPS/level point distribution
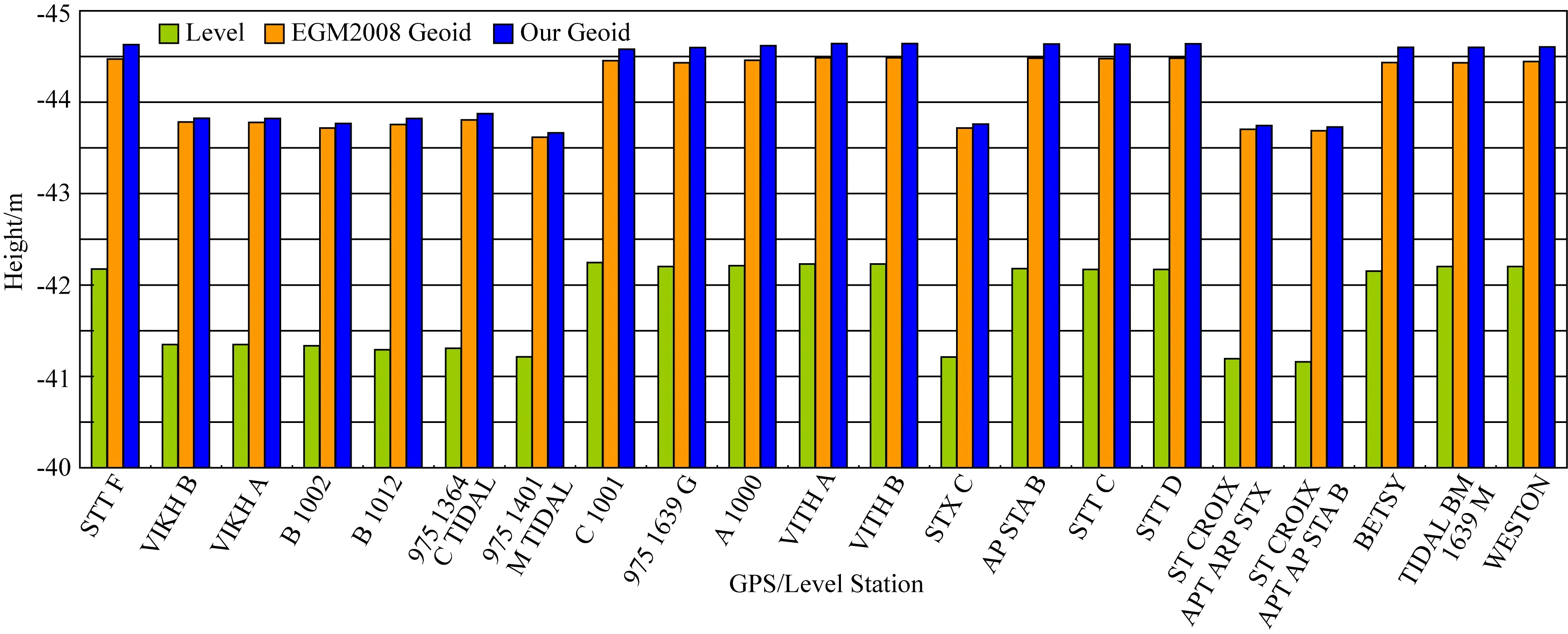
图8 水准面与EGM2008大地水准面及航空重力确定的大地水准面对比Fig.8 Geoid of GPS/level compared with the EGM2008 geoid and the geoid determined by airborne gravity data
4 结论
构建高精度大地水准面将是我国航空重力勘探下一步应用的重要方向,基于移去-恢复法思想,本文采用重力勘探中位场转换技术,特别是引入向下延拓的最小曲率方法,给出了一种快速构建海域大地水准面方法.方法通过移去EGM2008地球重力场,采用最小曲率法对移去后剩余的航空重力异常进行向下延拓并在频率域对其积分获取扰动位,最终通过结合EGM2008水准面模型实现对海域大地水准面精化.理论模拟和实际航空重力测量数据处理表明,尽管该方法在构建海域大地水准面存在位场转换近似,但具备较高的计算效率和精度,可为利用海域航空重力勘探成果快速构建大地水准面提供技术支撑.航空重力勘探属于相对重力测量,本方法需要结合地球重力场模型,使用的EGM2008等全球重力场模型在一定程度上限制了构建的海域大地水准面精度,我们希望同测绘学界进一步合作,共同构建我国自主的高精度全球重力场模型,进一步提升我国大地水准面的精度.
致谢本文图3使用了美国NOAA的数据,在此表示感谢.感谢两位匿名审稿专家对本文提出的批评和建议.
