奇异值趋势分解在燃油泵性能指数预测中的应用*

戴邵武，陈强强，戴浩然，孙玉玉

(1.海军航空大学 岸防兵学院，山东 烟台 264000；2.空军95596部队，河南 商丘 476000)

0 引 言

机载燃油泵在工作过程中为航空发动机提供规定的流量和压力燃油，是飞机燃油系统的核心构件之一[1]。机载燃油泵的工作状态直接程度的影响着飞行安全，因此对燃油泵进行可靠性分析及性能退化趋势预测具有重要的意义[2]。

在针对航空发动机参数进行准确预测的分析研究中，基于数据驱动的预测模型得到了充分的应用与发展。李晓白等人[3]采用经典的自回归滑动平均模型应用于航空发动机性能退化数据，并验证了该模型对提高短期预测精度的有效性。经典的数学模型具有严谨的理论推导，但针对复杂的时间序列存在着精度不足、模型不准确等劣势。刘永建[4]采用改进神经网络方法对发动机性能参数进行了预测研究，实现了航空发动机性能监控及趋势预测。但神经网络在使用过程中存在着参数选择无依据、训练时间较长等缺点。张建采用支持向量机对发动机排气温度裕度进行研究分析[5]，但支持向量机在使用过程中存在着易陷入局部极小化的缺陷。相比之下，最小二乘支持向量机(least square support vector machine，LSSVM)具有泛化能力强、精度高等优点，在航空发动机时间序列预测中具有更高的精度优势[6]。

随着航空发动机制造工艺趋于精密化、复杂化，同时工作环境也更加恶劣，航空发动机性能数据呈现出强烈的非线性、非平稳特征[7]。此时，单一的预测模型不足以完整概括其性能变化特征。

本文在研究过程中，采用奇异值分解(singular value decomposition，SVD)方法对原始数据进行处理以降低时间序列的复杂程度；同时在构建最小二乘支持向量回归(least square support vector regression,LSSVR)回归预测模型时，引入粒子群优化(particle swarm optimization,PSO)算法进行参数的自适应选择，增强了LSSVR预测模型的自适应性。将SVD-LSSVR算法应用于机载燃油泵性能指数退化数据，结果表明，该方法能够建立准确的预测模型并提高预测精度，是一种有效的预测方法。

1 基于SVD的趋势分析

机载燃油泵工作过程中，受到制造工艺、工作环境等多方面复杂因素影响，所采集到的压力信号具有多阶段与非线性的特点。燃油泵退化数据的非线性非平稳特征，体现了性能变化的实际情况[8]。如果对其性能退化数据进行直接预测，存在着预测模型建立不准确、预测精度不高等问题。因此可通过对原始性能退化数据进行分解以降低其时间序列复杂性。

SVD通过从时间序列中优化提取相关信息，从而实现原始数据的趋势项和去趋势项的分离[9]。SVD在使用过程中具有良好的数据稳定性，在数据分离、去噪声等方面具有广泛应用。设原始时间序列为

x=[x1,x2,…，xn]

(1)

步骤1对长度为n的时间序列x进行相空间重构，构建时间序列参数矩阵

(2)

式中m=[(n+1)/2]，[•]为取整运算。N=n-m+1。

步骤2对参数矩阵X进行奇异值分解

X=UΓVT

(3)

式中U∈RN×N,V∈Rm×m且均为正交矩阵。

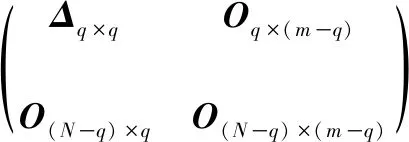
(4)

式中Δq×q=diag(δ1,δ2,…,δq),δ1≥δ2≥…≥δq>0为矩阵Γ的奇异值，q≤min(N,m)。

在SVD中，奇异值的大小反映了矩阵的能量分布。奇异值越大，其对应的信号占据矩阵的比重越大，越能够反映出信号的主要信息。根据需求不同，定义不同的信号成分。例如在去噪应用中，定义较大的奇异值对应信号的主要成分，较小的奇异值对应信号的噪声部分[10]；在本文的趋势分解中，定义较大的奇异值反映数据变化的主要成分(趋势项)，较小的奇异值反映数据变化的波动成分(去趋势项)。因此，通过确定趋势项的奇异值阈值，即可实现趋势项与去趋势项的分离。

步骤3确定阈值。在阈值确定过程中，根据奇异值的大小关系对奇异值分组，通过寻找奇异值的突变点即奇异值分布曲线的"肘部"实现趋势项分离[11]。取正整数为r，将取值较小的q-r个奇异值(对应去趋势项)置为0，则Γ可转换为

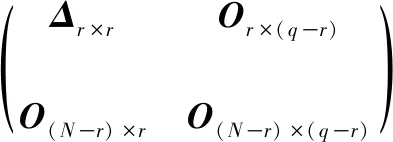
(5)

式中 Δr×r=diag(δ1,δ2,…,δr)。

步骤4输出趋势项与去趋势项。重构矩阵X′=UΓ′VT，即可得到原始序列对应的趋势项与去趋势项。

2 基于PSO算法的LSSVR

2.1 LSSVR

LSSVR是LSSVM的表现形式之一。LSSVR通过将二次规划问题转化为求解线性方程组问题，提高了求解问题的速度和收敛精度[12]。

设训练样本集为D={(xk,yk)|k=1,2,…,N}，其中xk∈Rn为输入数据，yk为输出数据。定义非线性回归函数[13]

f(x)=(w·φ(xk))+b

(6)

式中w为权向量，b为偏差量。可将函数估计问题转换为

(7)

式中ek为误差变量；r>0为规则化参数。

LSSVR的约束条件为

yk=(w·φ(xk))+b+ek,k=1,2，…,N

(8)

式中φ(·):Rn→Rnh为将原始空间映射到一个高维Hilbert特征空间的核空间映射函数。

定义拉格朗日函数如下

L(w,b,e,a)=J(w,e)-

(9)

式中ak≥0为拉格朗日乘子。

分别对w,b,e,a求偏导数，简化矩阵得到回归函数为

(10)

其中，惩罚因子控制对超过误差样本数据的惩罚程度，其大小直接影响模型的复杂性和稳定性；核函数参数反映了相关向量之间的相关程度，其大小与模型的精度和推广能力直接相关。

2.2 PSO算法

在惩罚因子和核函数参数的选择过程中，采用PSO算法完成其参数的自适应优化选择。PSO算法是智能领域算法中的一种基于群体智能的优化算法[14]。PSO算法于1995年由Kennedy和Eberhart提出，通过粒子在解空间追随最优粒子进行搜索。

3 组合预测算法

综上所述，本文提出的基于SVD和优化LSSVR的机载燃油泵性能指数组合预测方法流程为：1)采用SVD趋势分解方法，对采集到的机载燃油泵性能退化数据进行分解，得到趋势项和去趋势项；2)对步骤1中得到的趋势项和去趋势项序列分别构建LSSVR的预测模型，实现对分解序列的预测分析；3)采用PSO算法对LSSVR预测模型进行自适应参数寻优，以构建更加准确的预测模型；4)将趋势项与去趋势项的预测结果进行相加，得到最终预测结果。预测流程图如图1所示。

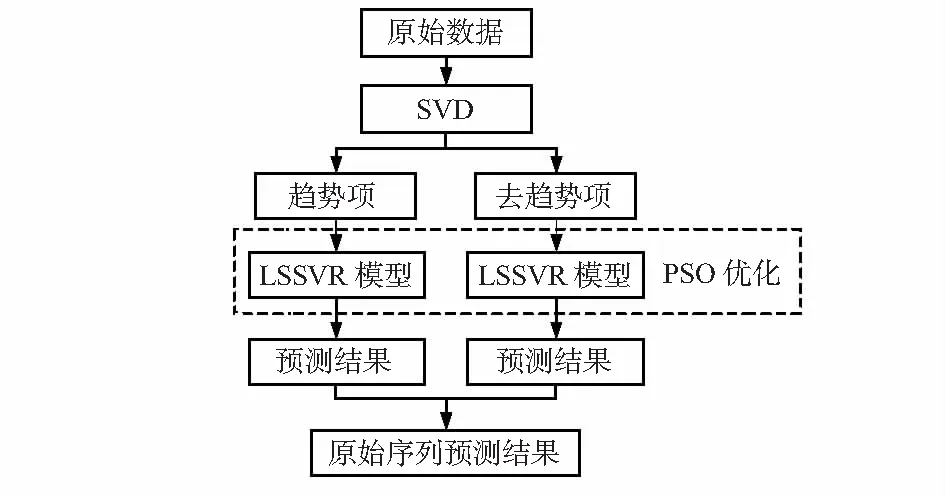
图1 预测流程图

4 实验分析

在实验室对某型机载燃油泵进行循环电压下的实验，在实验过程中，记录机载燃油泵出口压力传感器的输出值。选择设备开始工作后的195个循环中的压力值进行采集。得到压力信号随时间的退化曲线如图2所示。

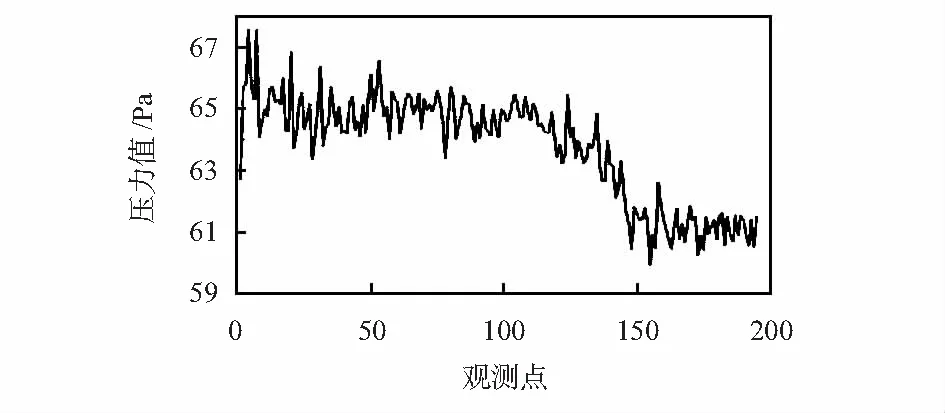
图2 机载燃油泵压力退化曲线

由图2可知，在观测过程中，机载燃油泵的压力信号呈现出多阶段的退化模式，在第1阶段平稳退化，之后有下降退化趋势，随后又趋于平稳状态。

根据SVD原理，确定奇异值矩阵Γ中的奇异值阶数如图3所示。

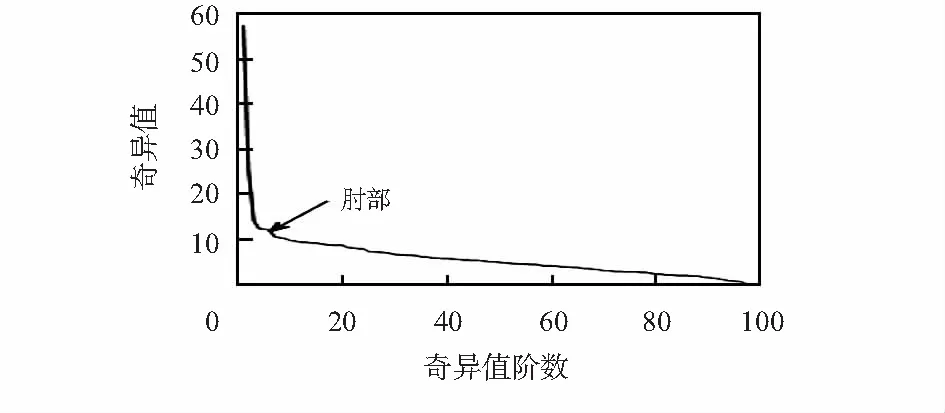
图3 确定SVD有效秩阶次

确定在SVD步骤3中的正整数r=7，得到SVD的趋势项和去趋势项结果如图4所示。

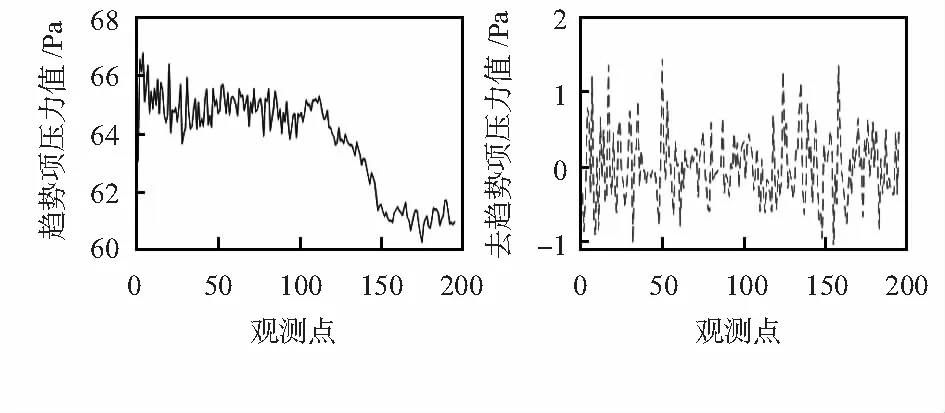
图4 SVD结果

如图4所示，经过SVD后，所得趋势项包含了原始时间序列的趋势信息，同时趋势项较为平稳，相比图4而言具有更小的非线性，因此可通过分解预测的思路提高预测精度。

为了验证基于SVD-LSSVR预测模型的准确性，选取样本数据的70 %作为训练集(约为140个数据)，余下30 %作为测试集(约为55个数据)，以均方根误差(root mean squared error，RMSE)和平均绝对误差(mean absolute error，MAE)为指标来衡量SVD-LSSVR算法对时间序列的预测能力，表达式如下[15]

(11)

(12)

式中Xreal,i为第i个数据的真实值，Xpre,i为第i个数据的预测值。

为了说明基于SVD的机载燃油泵趋势分解对提高时间序列预测精度的影响，采用直接对原始时间序列构造基于PSO参数优化的LSSVR预测模型进行对比验证。所得结果如图5所示。相比直接构建LSSVR预测模型而言，经过SVD后所构建的LSSVR预测模型具有更高的预测精度，预测误差更小，在预测结果上更接近于真实值。

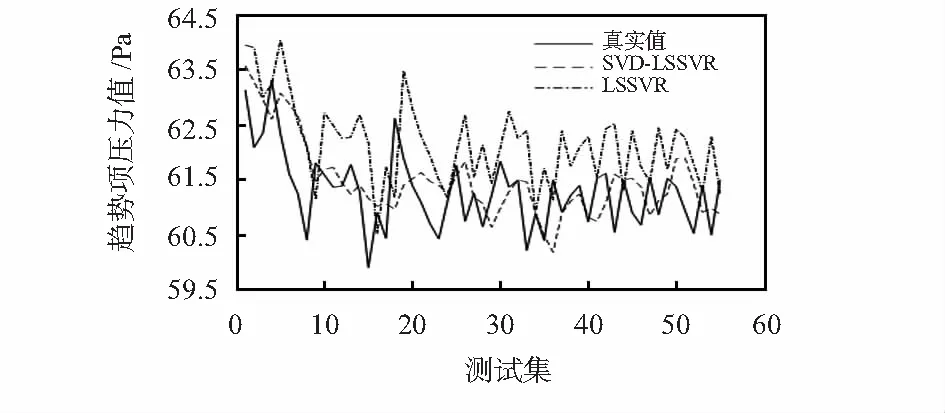
图5 预测结果对比

为了更直观展示预测结果并证明基于SVD趋势分解预测模型的优势，列出相应算法的预测指标如表1所示。

表1 预测误差

如表1所示，通过对预测误差进行分析可知:1) 由于原始机载燃油泵性能指数退化序列具有较强的非线性和非平稳性，直接构建LSSVR模型时存在着模型不准确、预测精度不足等缺点;2) 经过SVD趋势分解之后，所得趋势项的时间序列复杂程度降低，有助于构建准确的预测模型;3) 采用SVD-LSSVR算法进行预测，相比直接构建LSSVR模型而言，RMSE与MAE均具有明显的降低，证明了基于SVD-LSSVR算法的有效性。

5 结 论

本文采用趋势分解—预测的思想，针对机载燃油泵数据较为复杂、难以构建准确的预测模型问题，采用SVD方法对原始数据序列进行分解以得到趋势项及去趋势项，然后采用粒子群优化LSSVR的方法对分解得到的序列进行预测，最后将趋势项与去趋势项的预测结果进行汇总以得到预测结果，有效提高了预测精度。实验结果表明：1)采用SVD，能够有效降低原始时间序列的复杂程度，相比对时间序列直接进行分析，具有明显的精度优势；2)采用粒子群算法优化LSSVR模型，能够自适应的选择核函数参数及惩罚因子，提高预测结果的稳定性与精确性。