基于大尺度物理模型与2D数值网格的洪水淹没过程模拟

张 鹏

(河北省子牙河河务中心，河北 衡水 053000)

1 概述

在过去的几十年里，洪水造成了巨大的经济损失并且导致人们流离失所，因此防洪工作迫在眉睫。前人提出并实施了一些防洪方案，现行使用最多的方法是基于使用洪水淹没模型的洪水分析和预测，统称为实时洪水预报。

本文拟提出采用2D数值网格方法的来实现洪水预报。这种方法的原理是通过质量守恒在高分辨率地形中使用较粗的数值网格，由于自由水面比实际测深更平滑，故可以有效地用于计算自由水面高程的空间变异性，进一步利用子网格以提高地形信息的准确性。现有的文献中关于洪水淹没的大规模物理模型非常少，本文在实验室中建立了简化的河道及周边模型，共设有4个站点以研究洪水淹没的影响。为了量化网格数值方法的有效性和准确性，本文通过大型物理模型试验对2D洪水淹没模型进行了检验。

2 研究区域

滏阳新河归属于滏阳河流域，滏阳河是组成子牙河流域两大河系之一。子牙河流域是海河流域的重要组成部分，历史上海河流域发生特大洪水多以子牙河洪水为主。该流域历来是河北省防汛工作的重点。滏阳新河防护区人口密集，经济发达，地理位置和防洪地位非常重要。滏阳新河位于河北平原中东部地区，是“63.8”洪水后河北省1965年冬至1968年兴建的人工排洪河道，为治理海河的骨干工程之一，为滏阳河流域洪水的主要出路。主要任务是配合大陆泽、宁晋泊滞洪工程将滏阳河流域14877km2的洪水导入子牙新河。本文以艾辛庄下游河段形成的河漫滩平原区域为例，使用实地数据以25: 1的比例尺建立了物理模型，并使用缩略后的实地数据进行了2D洪水淹没数值模拟。

3 方法

3.1 物理模型

3.1.1模型的缩放

从水力学角度来看，缩放比例的物理模型和真实情况下的流动条件必须相似。五个表征流动的参数：弗劳德数、雷诺兹数、欧拉数、韦伯数和柯西数要满足真实流动情况。表面流动是一个受重力现象影响的自由表面过程，因此弗劳德显得至关重要，这要求重力和惯性力之间的比率(即弗劳德数)在模型和原型中相等。公式(1)为弗劳德数方程。

(1)

式中，v—水流的平均速度；g—重力加速度，L—深度。

3.1.2物理模型设置

物理模型与原型的比例为1∶25，总面积为23m×7m。表1显示了原型和物理模型的一些参数。

表1 原型和物理模型的参数

由于本文涉及到大规模的模型，需要合适的构造手段。构造步骤包括使用厚胶合板建立物理模型的下部基础、为物理模型边界建造墙，并设置通道和洪泛区(由横截面间隔为0.8 m的软胶合板制成)。在洪泛区横截面之间填充非黏性材料(沙子)，直至洪泛区横截面以下约2.5cm。沙层2.5cm以上的部分用混凝土混合物填充。最后将表面打磨光滑。经过一天的晾干护坡，用防水材料擦拭物理模型的表面。图1显示了物理模型的概况。

图1 物理模型的整体视图

3.1.3物理模型实验

在本研究中，4个站点分别对应4种不同的情形，情形1、情形2、情形3和情形4中对应4种不同的流量，分别为24、32、40、64 L/s(实际条件为75、100、125、150 m3/s)进行了物理实验模拟。然后，记录每个站的水面高度、流速剖面和洪水范围。使用无人机拍摄图像测量实地洪水面积，并利用ArcGIS软件进行分析。

3.2 数值模型

3.2.1HEC-RAS2D

使用由美国陆军工程公司水文工程中心开发的HEC-RAS建模系统。HEC-RAS广泛用于水力和洪水淹没建模，可以处理稳态和非稳态流动条件。对于稳定条件，它使用隐式有限差分格式，借助于从UNET模型改编的解算器来求解完整的圣维南方程。HEC-RAS的2D模型代码可以用于处理非恒定流条件的问题。该代码使用隐式有限体积格式来求解2D圣维南方程或2D扩散波。HEC-RAS基于网格测深方法实现子网格划分。该方法在建模过程中使用预先计算的手段来获取水力半径、体积和横截面积的最佳信息，用于洪泛区的模拟。

3.2.2模型模拟

以艾辛庄下游河段形成的河漫滩平原实地数据为基础，由无人机生成0.5 m分辨率的数字模型。在数值模拟中，根据实地河流的实际情况模拟了相同的入流。图2显示了数值模型的几何构造。使用的平均网格尺寸(黑线)为40m×40m(比数字高程模型分辨率大80倍)，使用的最小网格尺寸为23m×23m(比数字高程模型分辨率大46倍)。流出边界条件是自由流动，所有的模拟结果都是在水流处于稳定状态下1h后得到的。

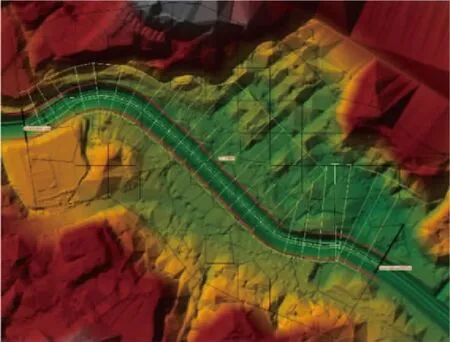
图2 模型的几何构造

河道中n(曼宁值)的取值范围为0.008至0.010，洪泛区的取值范围0.013～0.016。以1号站为参照站，使用平均绝对误差的拟合优度指数优化校准过程，平均绝对误差(MAE)和平均相对绝对误差(MRAE)定义如下：

(2)

(3)

式中，n—站点的总数；Xobs—1号站的实际观测值；Xmod—1号站的模型模拟值。

通过比较所有站点的洪水范围模拟结果和参照站实际观察到的洪水范围，对每个模型进行评估。图3将校准结果展示为两种曼宁值—MAE的等值线图，图中显示最佳值接近0。根据计算，曼宁渠道和洪泛区的最优值分别为0.0098和0.0153。

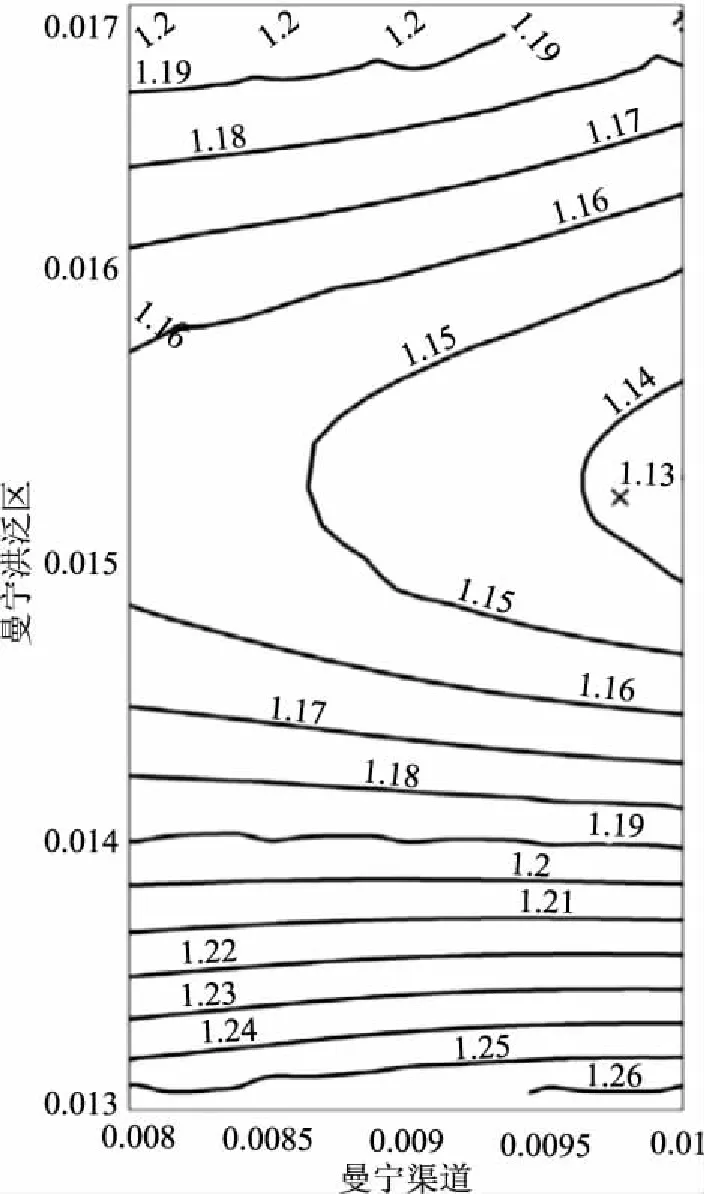
图3 参照站的平均绝对误差与两个模型参数的关系

4 结果和讨论

先从水面高程的角度研究数值模型的准确性，然后从洪水范围的角度讨论数值模型模拟物理模型实验的吻合度。

4.1 比较水面高程

图4—7显示了4个不同站点物理模型和数值模型沿河道水面高程剖面的比较情况。

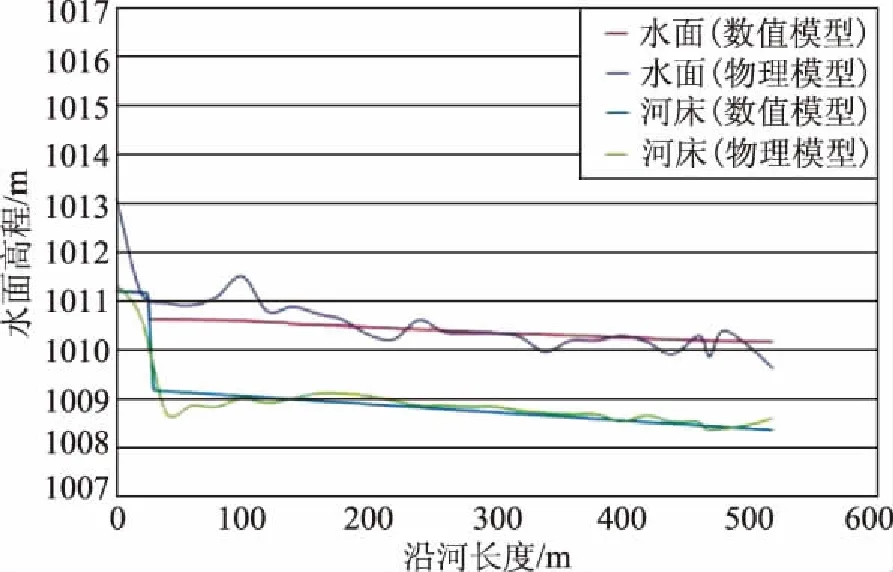
图4 流量为75m3/s的情况

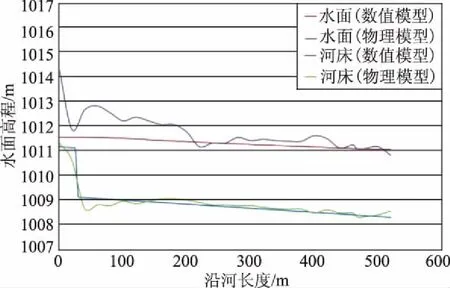
图5 流量为100m3/s的情况

图6 流量为125m3/s的情况

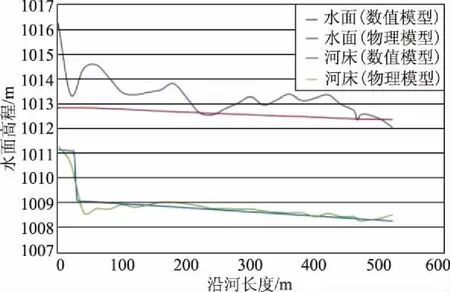
图7 流量为150m3/s的情况

4个站点的物理模型和数值模型的比较表明，物理模型由几个波动条件组成，这种波动随着流入值的增加而增加，波动发生的原因是1号站至4号站的河道坡度和宽度发生变化，其中4号站有一个水跃。由于直线通道导致流速开始增加，1号站处的流量急剧减少。在2号和3号站，弯道位置影响了WSE的波动。最终的结果表明物理模型和数值模型之间有良好的一致性，可见后文表2中对MAE和MRAE的分析。随着流入值的增加MAE的精度有略微降低的趋势，这是因为物理模型受到沿通道发生波动的影响。

4.2 比较洪水范围

图8—11展示了物理模型和数值模型的洪水范围结果比较。2、3、4三个站点的洪水范围模拟结果展现了与WSE的类似的趋势。

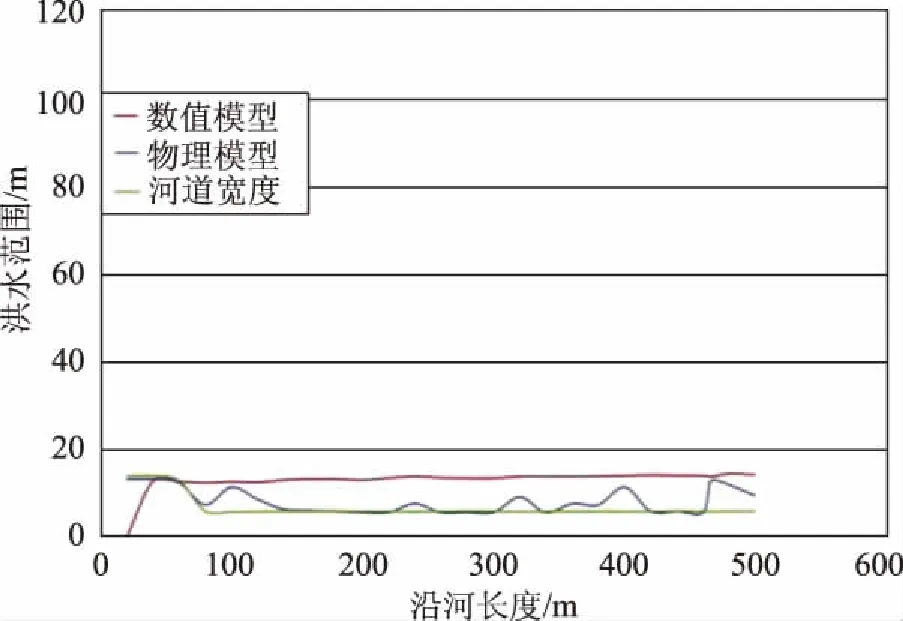
图8 流量为75m3/s的情况

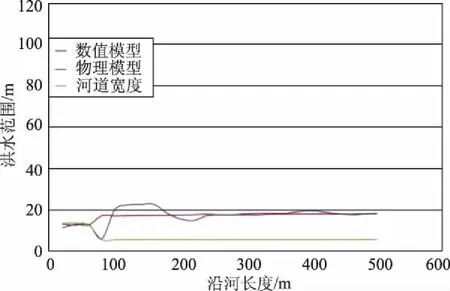
图9 流量为100m3/s的情况

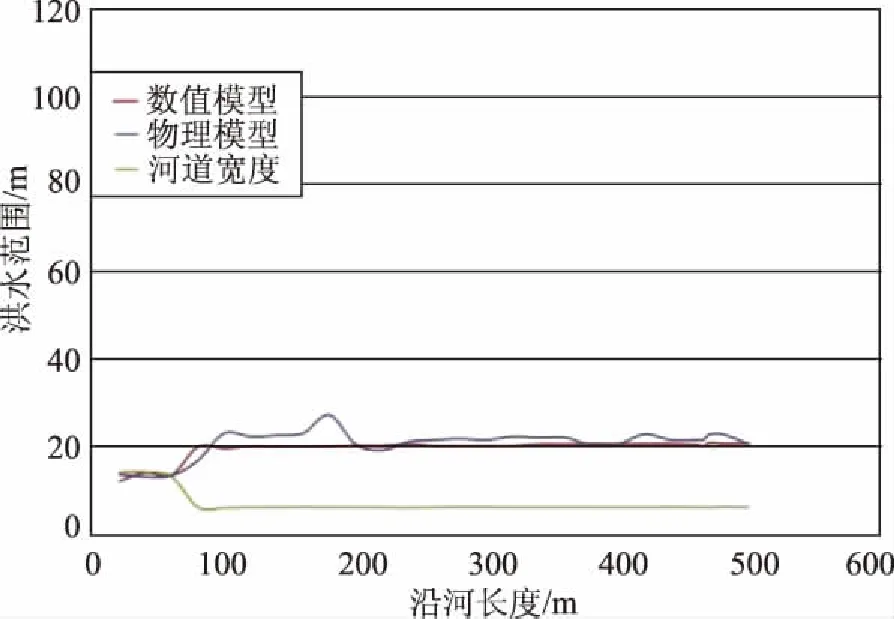
图10 流量为125m3/s的情况

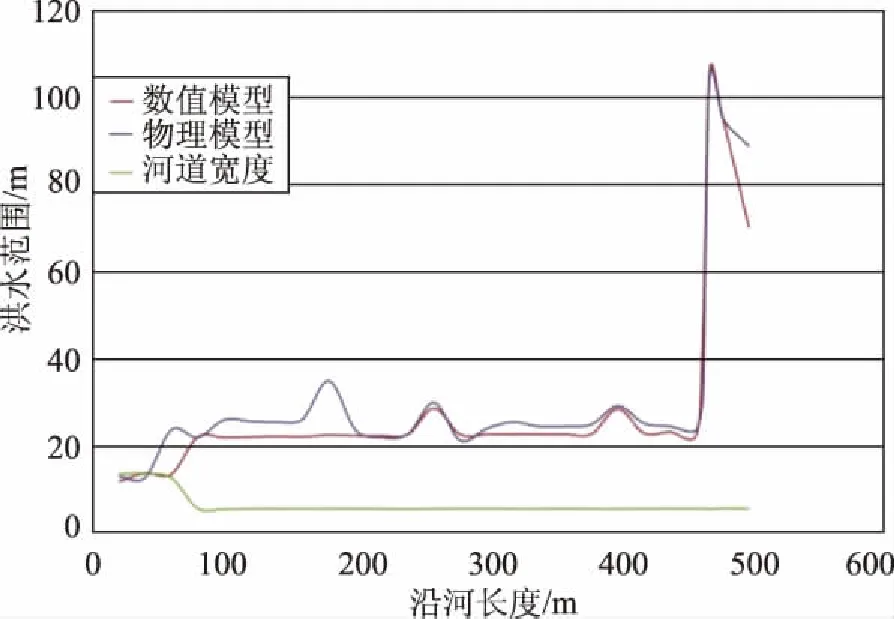
图11 流量为150m3/s的情况

对于站点1，结果与物理模型结果有显著差异。在20m处附近，没有洪水范围数据，这一结果与物理模型的WSE结果相反。虽然大网格尺寸可以用于模拟，但其精度将会失真，这一结果证实了模型模拟的网格设置还需要进一步的细化。

从沿河长度和洪泛区来看，物理模型和数值模型中都有4个发生溃决的位置，这种溃决是由于特定位置的地形高度造成的。沿河长度500m附近的溃决现象尤其明显，洪水范围可达到物理实验和数值模型的边界处(图11)。与其他位置相比，裂口的宽度也较大。这一结果表明，为了降低该河段范围内的洪水风险，需要在该地块修筑适当的排涝工程。

就数值模型模拟的准确性而言，站点1(最低流量)的MRAE最高误差值为0.832。这个差异与上述WSE的波动成因类似。表2展示了MAE与MRAE分析的细节。

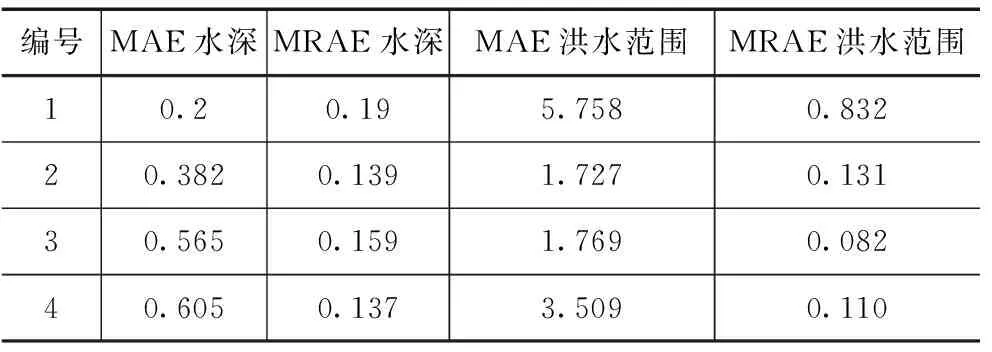
表2 MAE、MRAE水深和洪水范围比较结果

以上研究结果表明，数值模型的模拟结果与物理模型结果大致吻合，数值模型适合用于洪水淹没过程的模拟。

5 结论

通过设置不同的入流边界条件，采用与实地模型比值为1∶25的大型物理模型实验验证了2D数值网格模型的准确性。除最低入流边界条件下的洪水范围外，总体模拟结果表明物理模型与数值模型吻合度较好。出现的差异说明数值模型的网格设置还需要进一步的细化。研究证实了2D大网格模型具有模拟洪水的能力，体现了该数值模型具有良好的精度，且数值模型无论是从工作量还是经济性角度，均更适用，可以推广到实际工程的设计中。下一步的研究计划是如何将大网格细化为子网格，从而弥补在低来水量下模拟结果失真的缺点。