利用EXCEL绘制多规则功效函数图及操作过程规范图
2021-03-05张裕彭爱红余启华杨丽华
张裕,彭爱红,余启华,杨丽华
(湖南省第二人民医院 湖南省临床检验中心,长沙410007)
质控规则的选择和性能研究是目前临床实验室关心的问题,解决这一问题的主要途径是绘制功效函数图。目前绝大部分实验室不能自行绘制功效函数图和操作过程规范图,功效函数图软件的应用还不普遍[1]。电子表格具有方便易获取的特点,利用电子表格计算单规则的功效函数已有探讨[2]。本研究在基于单规则功效计算的基础上,分析多规则功效的计算原理并计算常用的几种多规则功效,绘制功效函数图和标准化操作过程规范图,在一定程度上帮助实验室人员进行手工实际操作。
1 多规则功效的计算
1.113s/22s、13s/22s/R4s规则的功效计算 质控规则的“功效”,即误差检出概率(probability for error detection,Ped),来源于标准正态分布,可以理解为不同误差条件下标准正态分布的概率变化[3]。Ped可理解为“失控”概率,未违背质控规则的情况则符合“在控”概率,1减去在控概率,即为该规则的Ped。以用2个水平质控物检测1次(N=2,R=1)时的13s/22s、13s/22s/R4s规则为例,首先分析质控数据的在控情况。根据质控规则的定义,质控数据将会落在5个区间中,分别为<-3s、-3s~-2s、-2s~2s、2s~3s、>3s,其中,落在<-3s和>3s区间的数据违背了13s规则,故可以排除这2个区间。因此,只需考虑2个质控数据(A和B)将落在剩下的3个区间中的情况。按照排列组合原则,将出现32(即9)种情况,其中可能出现的在控及失控情况见表1。Westgard指出[4-5],R4s规则可设定为1个质控数据>2s且另一个数据<-2s,还可设定为2个数据的差值>4s,因EXCEL自带功能有限,本研究只讨论前者,后者需用数学模拟软件进行模拟计算。
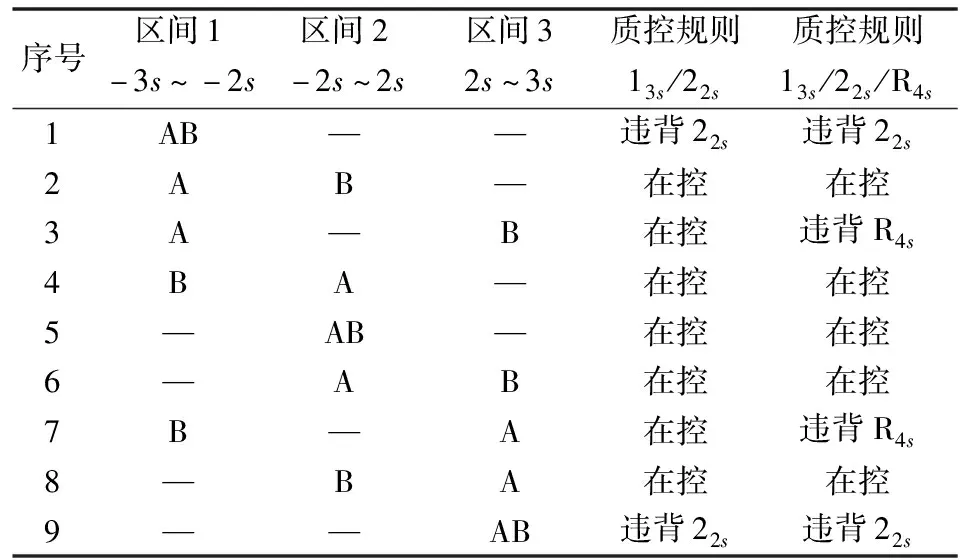
表1 13s/22s、13s/22s/R4s(N=2,R=1)可能的在控情况
通过观察表1中的在控情况,设定质控数据落在区间1的概率为a,区间2的概率为b,区间3的概率为c。计算13s/22s的在控概率算式为2*ab+2*ac+1*bb+2*bc,13s/22s/R4s的在控概率算式为2*ab+1*bb+2*bc。利用EXCEL中计算标准正态分布的累积分布函数NORMSDIST函数,可以算出上述规则发生不同系统误差时的功效,见表2。
表2为13s/22s、13s/22s/R4s(N=2,R=1)的EXCEL计算公式及功效值表,可以发现,13s/22s规则和13s/22s/R4s规则,除了假失控概率(probability for false rejection,Pfr)即系统误差为0时的Ped有0.000 9的差距外,其他系统误差时Ped几乎无差别。可见R4s规则在多规则组合中提升功效的作用极小。因为违背R4s规则的一部分情况已被13s规则排除,其次,随着系统误差的增加,违背R4s规则概率也越来越小。鉴于二者功效相近,因此使用13s/22s规则的实验室若增加R4s规则后并不用担心会导致失控情况明显增加。表2中最后一列为Parvin[6]利用一亿次数据模拟计算后得出的功效,可以发现,在系统误差<1时(西格玛度量值<2.65时),与EXCEL计算出的Ped仅有0.001 4~0.002 5的差距,归因于模拟计算时包括的R4s规则差值>4s的情况,随着系统误差的增加,这种情况发生的概率也越来越小,当系统误差>1.5时(西格玛度量值>3.15时),Ped几乎无差别。

表2 13s/22s、13s/22s/R4s(N=2,R=1)EXCEL计算公式及功效值
1.213s/2of32s、13s/2of32s/R4s规则的功效计算 利用上述原理,计算13s/2of32s、13s/2of32s/R4s规则(N=3,R=1)时的功效,需要先分析3个质控数据点(A、B、C)的在控分布情况,按照排列组合原则,将出现33(即27)种情况,其中13s/2of32s规则可能出现的在控情况有13种,13s/2of32s/R4s规则可能出现的在控情况有7种,见表3。

表3 13s/2of32s、13s/2of32s/R4s(N=3,R=1)可能的在控情况
通过观察表3中的在控情况,设定质控数据落在区间1的概率为a,区间2的概率为b,区间3的概率为c。计算13s/2of32s规则的在控概率算式为6*abc+3*abb+3*bbc+1*bbb,13s/2of32s/R4s规则的在控概率算式为3*abb+3*bbc+1*bbb。利用NORMSDIST函数,可以算出上述规则发生不同系统误差时的功效,见表4。
通过比较表4的功效数据可以发现和表3类似的特点,13s/2of32s规则与13s/2of32s/R4s规则有相似的功效。EXCEL与模拟计算出的Ped仅在极低西格玛度量值范围时有微小的差距,其他范围的功效几乎一致。

表4 13s/2of32s、13s/2of32s/R4s(N=3,R=1)EXCEL计算公式及功效值
1.313s/22s/R4s/41s规则的功效计算 利用上述原理,计算13s/22s/R4s/41s规则(N=4,R=1)的功效,需要先分析质控数据点的分布情况。与前面的多规则不同,4个质控数据点将会落在7个区间中,分别为<-3s、-3s~-2s、-2s~-1s、-1s~1s、1s~2s、2s~3s、>3s。其中,落在<-3s和>3s区间的数据违背了13s规则,故可以排除这2个区间。因此,需考虑4个质控数据(A、B、C、D)落在剩下的5个区间中的情况。按照排列组合原则,将出现54(即625)种情况。其中,违背22s规则的情况有220种,排除后剩下的情况中违背R4s规则的情况有108种,排除后剩下的情况中违背41s规则的情况有10种,最终在控的情况为287种,若在传统Westgard多规则需12s启动的情况下[7],则在控情况为289种(包括了A、B、C、D均在-2s~-1s和1s~2s的2种情况)。因数据较多,本文只列出最终计算出的功效与使用质控软件Westgard Advisor模拟的功效数据,见表5。
通过表5可以看出,存在289种在控情况下的功效比287种的功效要略低,但更接近于Westgard Advisor模拟的功效,两者的功效相差甚微。而287种在控情况的功效更高,因其判断失控情况更加严格。

表5 13s/22s/R4s/41s(N=4,R=1)2种情况下的功效
2 绘制多规则功效函数图及操作过程规范图
综合上述计算方法算出的功效,可以绘制出多规则的功效函数图,因13s/22s与13s/22s/R4s功效相近,13s/2of32s与13s/2of32s/R4s功效相近,故都只绘制后者,13s/22s/R4s/41s规则此处为289种在控情况时的功效。3种多规则功效函数图见图1,图形显示3种多规则的Pfr均很低,其中多规则13s/22s/R4s/41s因组合的规则和N最多,因此Pfr和Ped为三者中最高。

图1 3种多规则功效函数图
操作过程规范(operational process specifications,OPSpecs)图[8]显示的是测定方法的不精密度、偏倚和备选质控规则之间的一种线条图。绘制OPSpecs图的关键在于,计算出在指定Ped,如90%、50%时,备选质控规则的临界系统误差(ΔSE)。可利用EXCEL的单变量求解功能计算[2],或是在上述计算公式表格中SE处输入一个合适的可使Ped等于0.90或0.50的值。5种多规则的Pfr以及在具有90%Ped时的ΔSE、西格玛度量值和允许不精密度取值见表6。可以发现,13s/22s与13s/22s/R4s规则的ΔSE一致,13s/2of32s与13s/2of32s/R4s规则的ΔSE一致,故都只绘制后者,OPSpecs图见图2。图中可发现13s/22s/R4s和13s/2of32s/R4s规则可以完全保证5西格玛度量值水平检测系统的质量,13s/22s/R4s/41s可以完全保证4西格玛度量值水平检测系统的质量,符合Westgard六西格玛规则[9]设计的方案。

表6 具有90% Ped时5种多规则的ΔSE及允许不精密度

图2 3种多规则具有90%Ped的标准化操作过程规范图
3 小结
质控规则分为单规则和将多个单规则组合起来的多规则质控程序。常用的单规则如13s、13.5s在判断失控情况时非常方便,但单规则往往只对随机误差敏感,并且提供的Ped有限。而多规则尽管在判断失控时相对麻烦,但其优点是可以在保持较低的Prf的同时,提供更高的Ped[5],并且根据组合的规则不同,可以反映多种误差类型和趋势性变化。利用EXCEL计算多规则的功效,能帮助理解多规则功效的原理,方便手工应用,但随着组合的规则越多,N越大,质控数据的分布将越复杂,计算将变得繁琐。实验室在缺乏专业质控软件的情况下,可利用上述方法计算常用多规则的功效并绘制功效函数图和标准化OPSpecs图,结合单规则质控方案,进行更加丰富的个性化室内质控设计。
