轴流转桨式水轮机协联关闭规律选择及优化分析
2021-03-05张小莹周天驰张晓炜
王 苗,张小莹,周天驰,张晓炜
(1.新疆农业职业技术学院,新疆 昌吉 831100;2.新疆农业大学水利与土木工程学院,乌鲁木齐 830052;3.中国电建集团华东勘测设计研究院,杭州 310000)
0 引 言
由于地形地质条件的限制,很多水电站常常采用明渠结合有压管道的引水系统布置形式,这在中小型电站中尤为常见[1],此类电站又称无压引水式电站。为了满足上游河道的灌溉要求或者通航要求,无压引水式电站引水明渠的水位和流量变化往往较大,一般定桨式机组的高效区难以涵盖较大的水头区间,因此此类电站通常安装轴流转桨式水轮机,以利用不同水头和流量组合,提高发电效率[2]。
与混流式水轮机或者轴流定浆式水轮机相比,轴流转桨式水轮机的桨叶和导叶能随着水头和流量的变化而相应的开大或者关小,保证机组一直运行在高效率区,提高发电量。但是当电站发生甩负荷时,由于桨叶调节的存在,其关闭方式与定桨式水轮机有所不同:桨角开度变化的存在相当于关闭规律多了一个维度。所以无论是关闭规律选择还是优化方面,采用轴流转桨式机组的水电站水力过渡过程计算都较定桨式复杂。
近些年,国内许多学者在轴流转桨式水轮机过渡过程方面做了很多研究[3-5],在特性曲线处理方面,张蓉生[6]分析了传统几何方法处理综合特性曲线的二重性,引入德洛内三角网剖分方法对数据插值,该方法能够较好地处理转桨式机组的协联曲线。在轴向水推力方面,彭小东[7]给出了采用轴流式机组的水电站在过渡过程计算中应当注意的问题,讨论了轴流转桨式机组的蜗壳长度直径当量计算的方法以及轴流式机组的力矩、流量和轴向水推力的仿真计算方法。目前对其关闭规律的选择和优化方面研究较少,而在水电站调节保证计算中,合适的导叶-桨叶动作方式可以起到改善蜗壳压力、降低机组转速、减小轴向抬机力的作用,这是一种低成本而又高效的优化手段。
本文通过理论分析转桨式水轮机的协联飞逸曲线,结合实际工程实例,分别使用桨叶关闭、桨叶不动以及桨叶开启的动作规律(3种动作规律中导叶均一段直线关闭),计算甩负荷时蜗壳末端压力和机组转速上升率,据此选择合适的桨叶动作方式。在确定电站甩负荷时桨叶动作方式之后,采用可以用于多控制工况的导叶关闭规律优化非线性模型,运用模拟退火算法优化转桨式水轮机导叶的两段折线关闭规律,最后得到较优的导叶桨叶协联关闭规律。
1 协联关闭规律选择
1.1 理论分析
安装混流式机组的水电站发生甩负荷过渡过程时,导叶动作方式有一段直线关闭、两段直线关闭[8](先快后慢应用于低比转速水轮机,先慢关后快关应用于高比转速水轮机)、多段直线关闭[9]等;安装可逆式机组的抽水蓄能电站中,除了以上关闭规律之外,还有先延迟再直线关闭的关闭规律[10],其原因主要是考虑了可逆式机组S区的反水泵效应。总而言之,水电站导叶关闭规律的选择应该根据电站布置情况和水轮机特性进行综合考虑和具体分析。
转桨式水轮机的桨叶和导叶均可动作,由于桨叶调节的加入,转桨式水轮机的甩负荷过渡过程与常规定桨式差别较大,所以其关闭规律选择较为复杂。一般工程中发生甩负荷时,机组常用的关闭规律是在机组导叶快速关闭以快速削减水流,而桨叶也同时缓慢关闭。下面通过分析转桨式水轮机的协联飞逸曲线图,从理论上选择适合轴流转桨式机组的较优导叶-桨叶动作方式。
图1中为某轴流转桨式水轮机的协联飞逸曲线图,图1中实线为桨叶开度线,从左到右依次增大,而虚线为导叶开度线,从下到上依次增大。分析如下:对于同样的导叶开度,桨叶开启的越大时,水轮机的飞逸转速越低;对于同样的桨叶开度,导叶开启的越大时,水轮机的飞逸转速越高。所以在甩负荷过渡过程中,若导叶关闭的同时,桨叶快速开启,在导叶完全关闭之前,桨叶开度达到最大值,机组最大转速上升率将会降低。
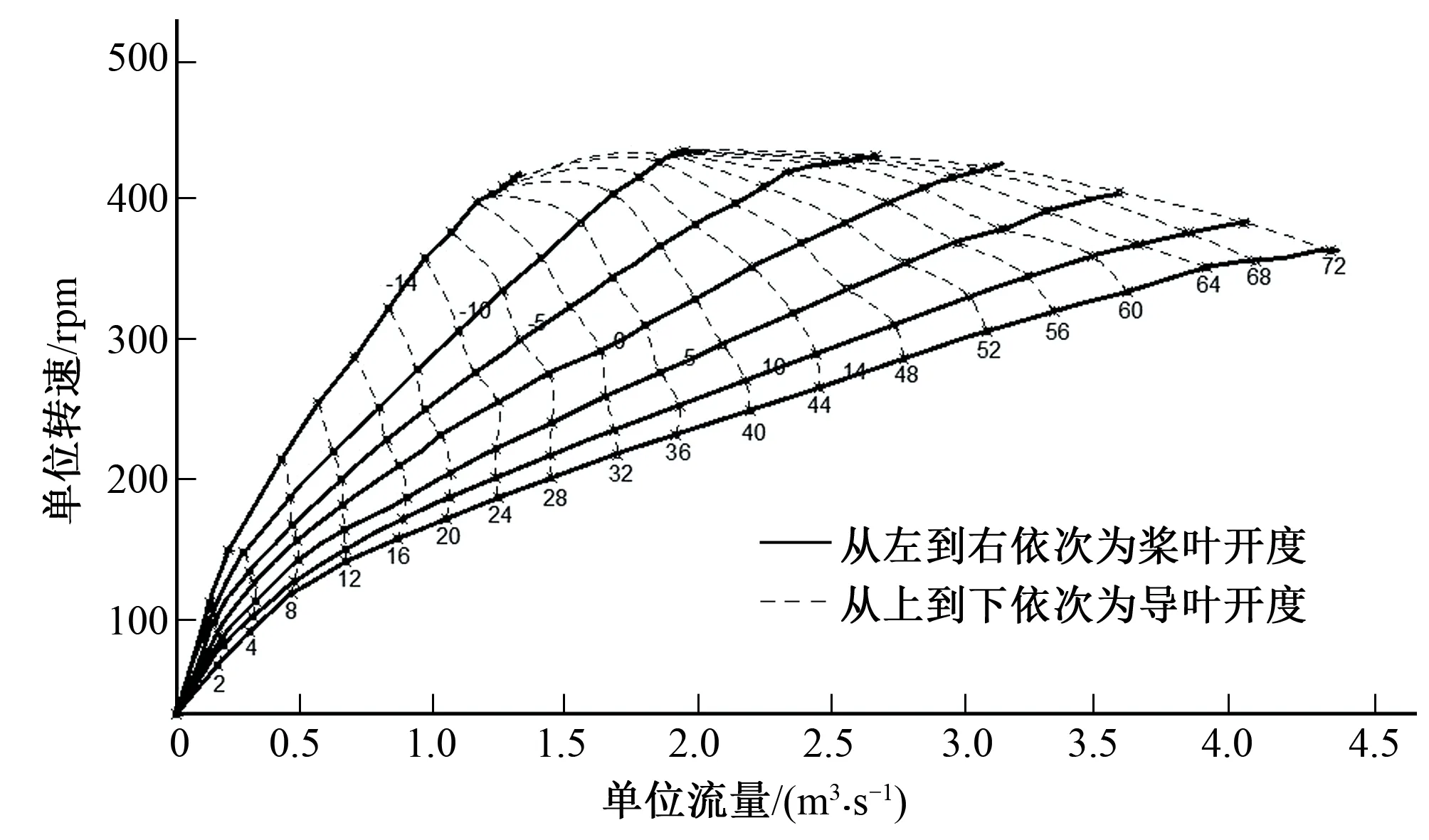
图1 某轴流转桨式水轮机的协联飞逸曲线图Fig.1 Runaway curve of a Kaplan turbine
根据上述分析,可以对转桨式水轮机提出一种新的关闭规律:当电站发生甩负荷时,导叶一段直线或者两段直线快速关闭,桨叶一段直线开速开启。由轴流转桨式水轮机的特点可知,这种关闭规律能够大大降低甩负荷过程中的机组转速和水锤压力。为了验证以上分析的正确性,采用特征线法[11],基于某一工程实例进行甩负荷过渡过程数值仿真计算。
1.2 实例验证
基本资料:某明渠引水式水电站装有3台卡普兰式(轴流转桨)水轮机,总装机140 MW,采用单管单机的布置形式,水轮机的额定水头22.5 m,额定流量227.5 m3/s,额定转速125 r/min,额定出力48.11 MW。输水系统包括引水明渠、前池、压力钢管、尾水管、尾水池、尾水明渠等。其中引水渠长约560 m,宽40~150 m,尾水渠长约382 m,宽90 m。
调保计算要求:蜗壳末端最大压力不超过55 m,机组转速最大上升率小于50%,尾水管进口最小压力不低于-8 m。电站运行控制工况如下:
工况一:上游水位为校核洪水位78.90 m,下游水位为校核洪水位60.30 m,3台机组以最大出力运转,某一时刻,所有机组同时甩全部负荷。该工况为蜗壳末端压力的控制工况。
工况二:上游水位为75.00 m,下游水位为全厂机组满发尾水位51.75 m,3台机组额定水头,额定流量,以额定出力运转,某一时刻,所有机组同时甩全部负荷。该工况为机组转速上升率的控制工况。
仿真计算模型中包含引水明渠、前池、压力钢管、机组、尾水管、尾水池、尾水明渠。本水电站发生甩负荷时导叶的关闭时间较短(10 s以内),在这个很短的时间内,前池水位升高,尾水池水位降低,但变化幅度均很小(经计算不到0.1 m)。导叶关闭之后,前池和尾水池中的水位呈现出周期性的波动并逐渐衰减,其中前池波动幅度约1.7 m,波动周期约270 s,尾水池波动幅度和周期略小于前池。由于前池和尾水池水位波动幅度远小于导叶关闭引起的水锤压力,且水位波动周期远大于水锤周期,所以前池和尾水池的水位波动对调节保证极值没有影响。
根据大量试算,水轮机导叶采用8 s一段直线关闭规律较为合适。在此基础之上,采用不同的桨叶动作规律对工况1和工况2进行过渡过程计算,工况1桨叶初始开度为4.14°,工况2桨叶初始开度为8.67°。
桨叶动作规律1:30 s一段直线关闭,关闭至-14°;
桨叶动作规律2:始终保持开度不变;
桨叶动作规律3:30 s一段直线开启,开启至14°。
不同桨叶动作规律的计算结果如表1及图2~5所示。
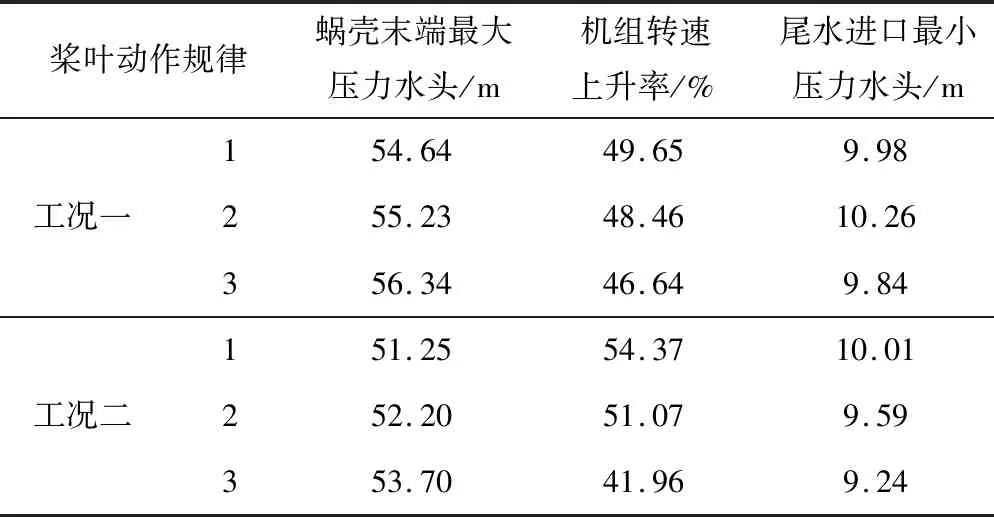
表1 不同桨叶动作情况下计算结果Tab.1 Calculation results under different blades actions
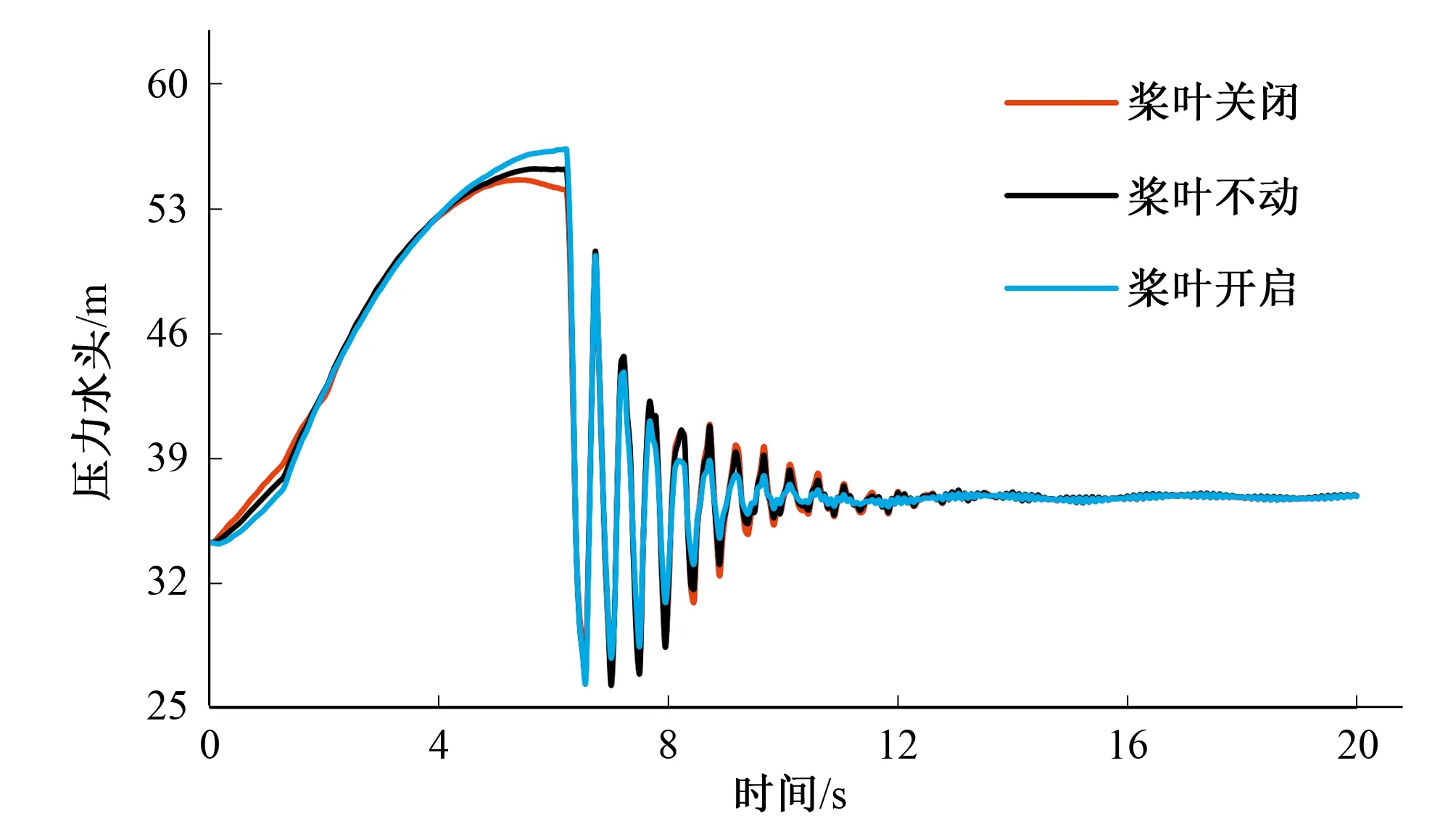
图2 蜗壳末端压力随时间变化图(工况一)Fig.2 Pressure change with time at the volute end (condition 1)
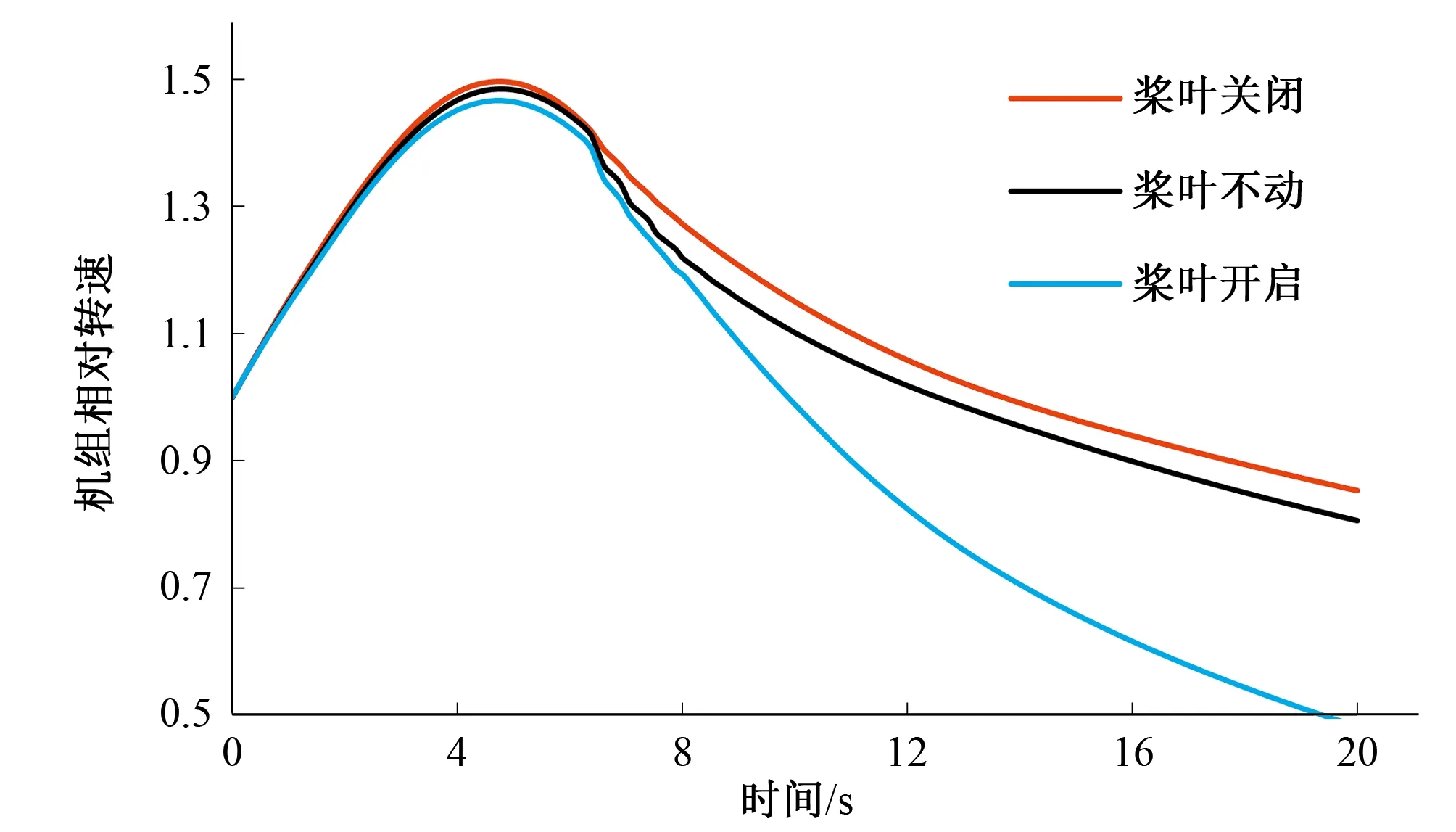
图3 机组相对转速随时间变化图(工况一)Fig.3 Relative speed change with time of the unit (condition 1)
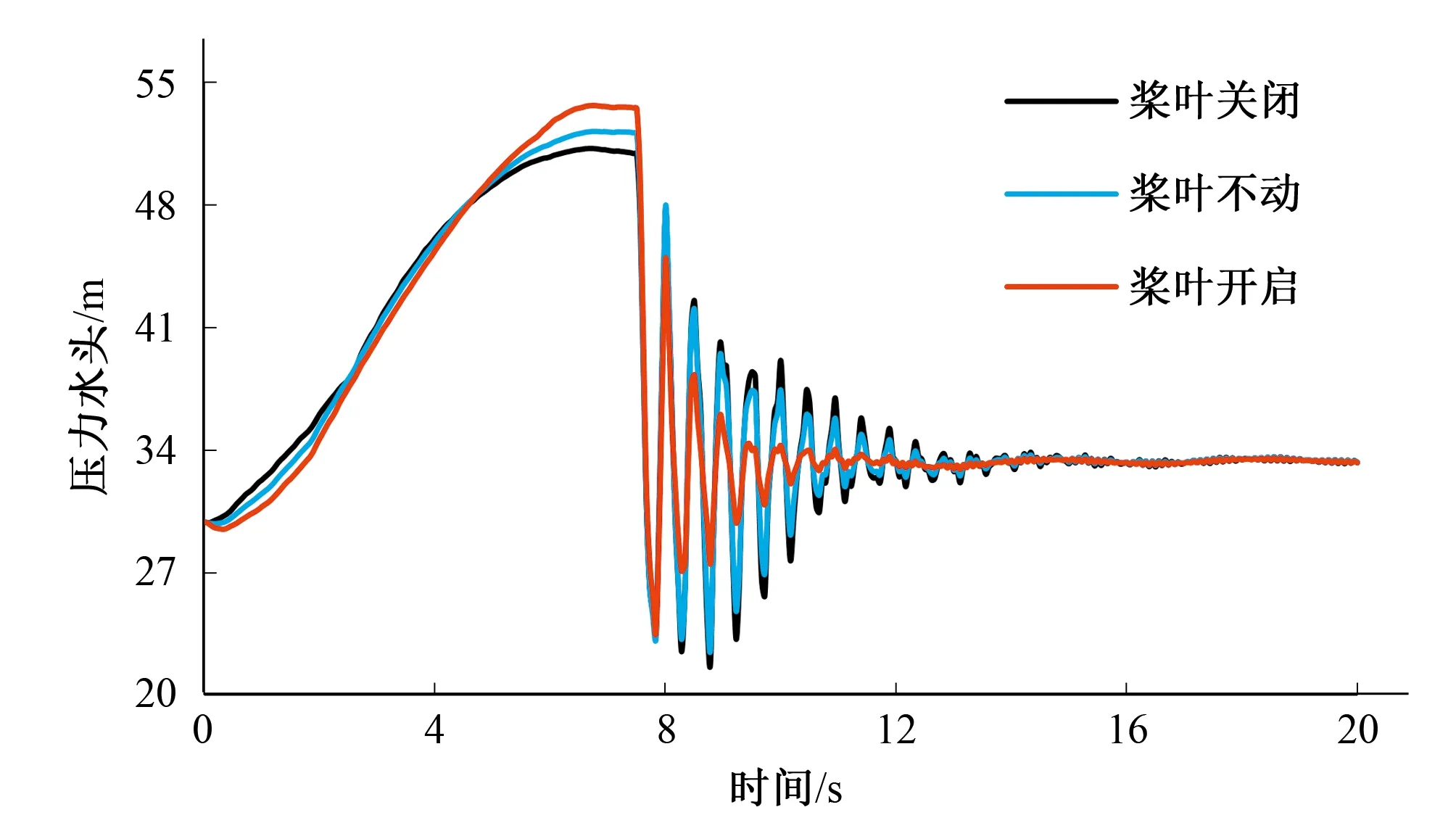
图4 蜗壳末端压力随时间变化图(工况二)Fig.4 Pressure change with time at the volute end (condition 2)
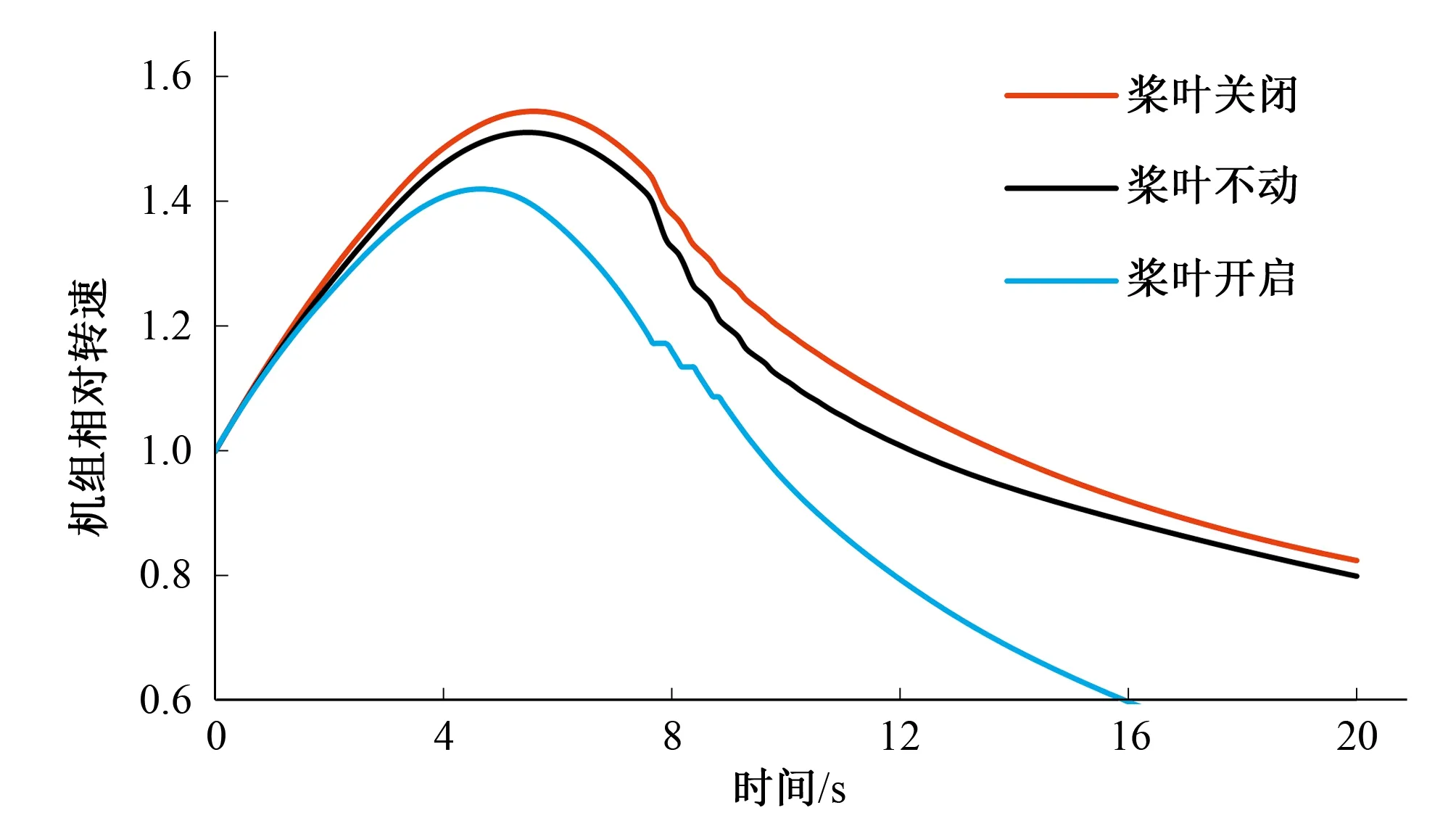
图5 机组相对转速随时间变化图(工况二)Fig.5 Relative speed change with time of the unit (condition 2)
由表和图可以看出:当水轮机导叶采用相同的一段直线关闭规律,桨叶依次采用开启、不动作、关闭的动作方式时,机组最大转速上升率有了明显的降低,而蜗壳末端最大压力有了微小的升高(桨叶30 s开启与30 s关闭相比,机组最大转速上升率从54.37%下降到46.64%,下降了14%;蜗壳末端最大压力从54.30 m上升到了56.20 m,仅仅上升了3.38%)。
机组最大转速上升率下降的原因是因为在桨叶开度较大情况下,机组的飞逸转速较小,由此可以推测:甩负荷过渡过程中,桨叶开启越快,机组转速上升率的降幅越大。所以采用桨叶开启的方式,虽然在一定程度上会造成蜗壳末端压力上升,但其增加值与机组转速最大上升率的降低值相比小了很多,若将导叶关闭时间缩短,可以达到同时改善两者的效果。因此该桨叶动作方式总体来说对水电站调保计算是有利的。
下面通过机组流量分析压力上升原因。图6为某一固定桨叶开度下的综合特性曲线图,图7~8分别为两个工况下过渡过程计算中流量变化过程线。
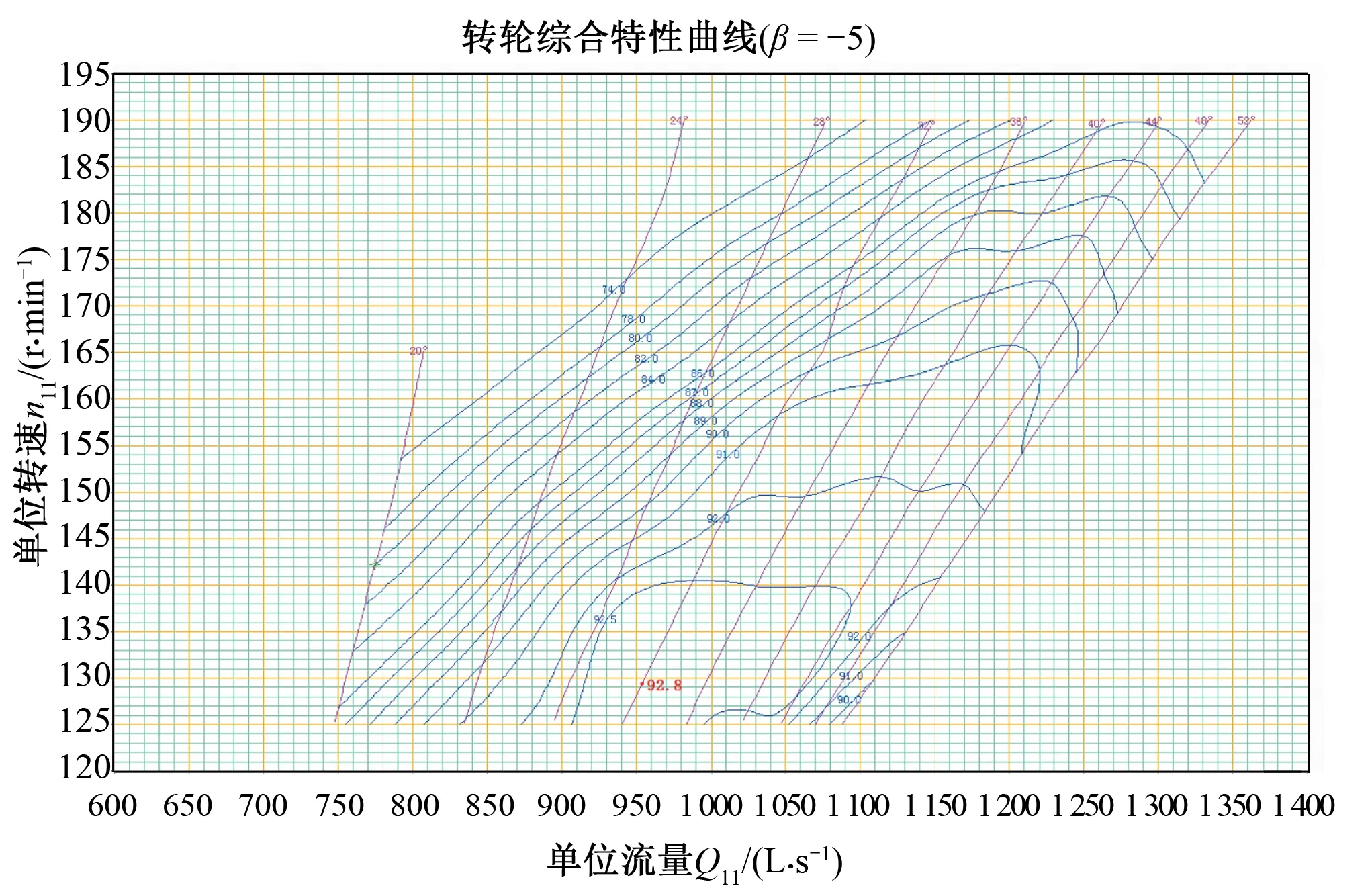
图6 某一固定桨叶开度下综合特性曲线Fig.6 Turbine synthetic characteristic curve in a fixed blade opening
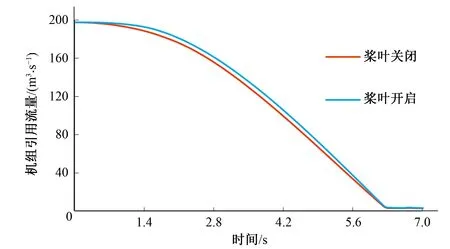
图7 机组流量变化图(工况一)Fig.7 Unit flow change with time (condition 1)
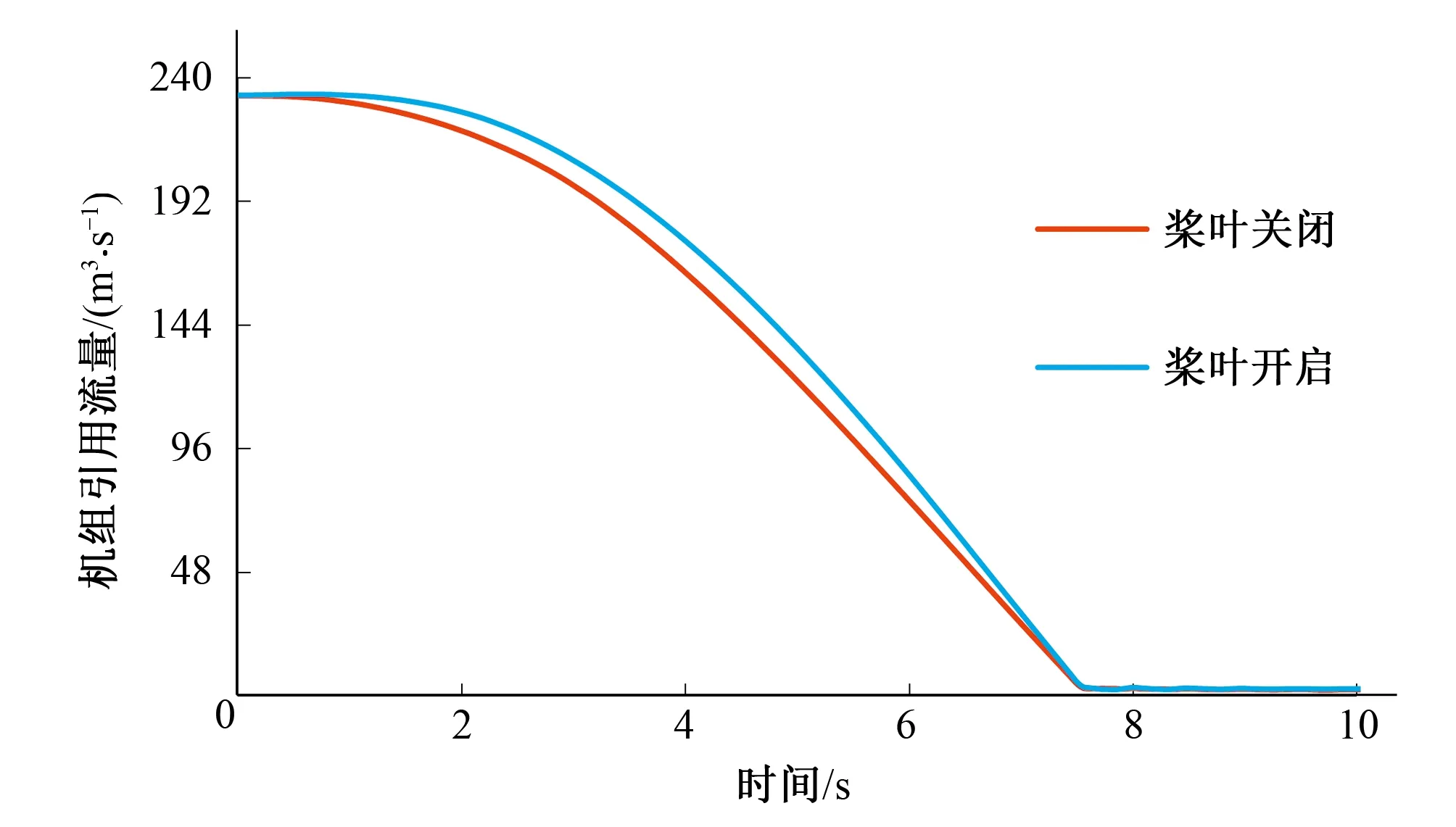
图8 机组流量变化图(工况二)Fig.8 Unit flow change with time (condition 2)
从综合特性曲线图中可以看出,该水轮机的比转速较高,对于相同导叶开度,单位转速越大,单位流量越大,因此理论上适合采用先快后慢的关闭规律。而由两个工况的流量变化图可以看出,桨叶开启与桨叶关闭相比,其流量减小规律略微呈现出先慢后快的特点,这对蜗壳末端最大压力不利。
综上所述,在甩负荷过渡过程中,在导叶关闭的同时桨叶快速开启可以明显降低机组转速上升,而蜗壳末端最大压力略微增加。通过选用合理的导叶关闭与桨叶开启规律,可以有效地平衡蜗壳末端最大压力和机组最大转速上升率,使两者均有较大的安全裕量。
2 导叶关闭规律优化
机组导叶采用两段折线关闭规律通常能够同时降低甩负荷过程中的蜗壳末端最大压力和机组最大转速,但两段折线关闭规律涉及的变量多,变量取值范围广。常规的优化方法是随机选择几组不同的关闭规律进行仿真计算,然后选择计算结果较好的那组关闭规律作为实际工程使用,这种方式无疑具有很大盲目性,选择结果的优良主要依赖于设计人员的经验。为了解决这一问题,本节采用一种非线性的导叶关闭规律的优化模型,通过一种智能优化方法----模拟退火优化算法,对上一节中初步计算得到的导叶-桨叶协联动作规律进行优化计算,得出符合调保计算的较优动作规律。
2.1 优化模型
评价函数:
(1)
式中:Hv,con、Nt,con、Ht,con分别是机组蜗壳最大内水压力、机组转速最大上升率、尾水管最小内水压力的控制值;Hmax、Nmax、Hmin分别是蜗壳最大内水压力、机组转速最大上升率、尾水管最小内水压力的计算值;a,b,c分别3个调保参数的权重系数;k为评价值放大系数;E为关闭规律的评价值。
由于蜗壳末端最大压力和机组转速最大上升率可能发生在不同的工况中,所以优化计算应该采用可以进行多工况计算的优化模型:
Hmax=(Hmax,1,Hmax,2,…,Hmax,n)
Nmax=(Nmax,1,Nmax,2,…,Nmax,n)
Hmin=(Hmin,1,Hmin,2,…,Hmin,n)
(2)
式中:n是参与优化计算的工况个数;Hmax,i,Nmax,i,Hmin,i分别是各个工况下计算出来调节保证计算指标值(i的取值范围为1~n);Hmax,Nmax,Hmin分别是所有工况中相应调节保证计算指标的最大值[12]。
2.2 模拟退火算法
模拟退火算法是一种新型的多目标优化计算方法,在诸多领域均有广泛的应用,其中水利领域中的水资源优化配置[13]、梯级水电站调度[14]等复杂问题的优化计算有较好应用效果。由于篇幅限制,算法的具体优化原理和计算步骤可见参考文献[12],这里不再详述。
2.3 优化计算
下面基于水轮机导叶关闭规律优化模型和模拟退火算法,对两段直线导叶关闭规律进行优化(桨叶均采用30 s一段直线开启的动作规律)。
优化算法的参数设定为:初始温度设置为1 000 ℃,每个温度值下优化3次,结束温度设置为5 ℃。即初始状态温度设定为1 000 ℃,在该温度下随机给定一个两段折线关闭规律,进行过渡过程计算,并采用评价函数计算评价值,作为初始条件。接着在当前关闭规律的基础之上,在一定范围内随机产生一个新的两段折线关闭规律,并进行过渡过程计算,根据计算结果计算评价值,若新评价值比原评价值好,则接受新的两段折线关闭规律为当前温度下的最优解,否则按照一定概率拒绝接受新的两段则先关闭规律(此概率与状态温度有关,温度越高,此概率越大)。在该温度下进行3次优化计算,然后根据预先设置好的冷却进度表降低状态温度。在新状态温度下进行3次以上优化过程,然后继续降低状态温度,最终停止优化的条件是状态温度降低至5 ℃。
根据2.2节的计算可知,由于该电站尾水管比较短,尾水管进口最小压力在导叶采用直线关闭规律时已经满足调节保证计算要求,所以优化函数中可以剔除尾水管进口最小压力这一项。而此电站中的蜗壳末端最大压力和机组最大转速上升率均是比较重要的控制指标,所以两者的权重系数给相同大小。
为了保证优化计算结果的可靠,分别采用3个不同的初始关闭规律U01=(7,8,0.4)、U02=(9,8,0.4)、U03=(8,8,0.7)进行多次计算,优化结果如图9所示。

图9 3次优化计算得到的关闭规律示意图Fig.9 Three closing laws obtained by optimization calculation
根据示意图可知3个不同初始关闭规律优化计算得到的结果基本一致:Ub1=(4.40,17.41,0.57)、Ub2=(4.71,16.28,0.57)、Ub3=(4.60,17.47,0.58),说明优化计算是可靠和稳定的。对比3个优化计算结果,无论初始关闭规律给定的是一段直线关闭还是分段直线关闭,无论给定的初始折点开度是多少,通过模拟退火算法计算,都可以优化得到相近似的结果,这说明优化计算的过程是稳定的。将Ub1、Ub2、Ub33种折线关闭规律分别带入工况一和工况二中进行数值仿真计算,计算得到的结果如表2所示:
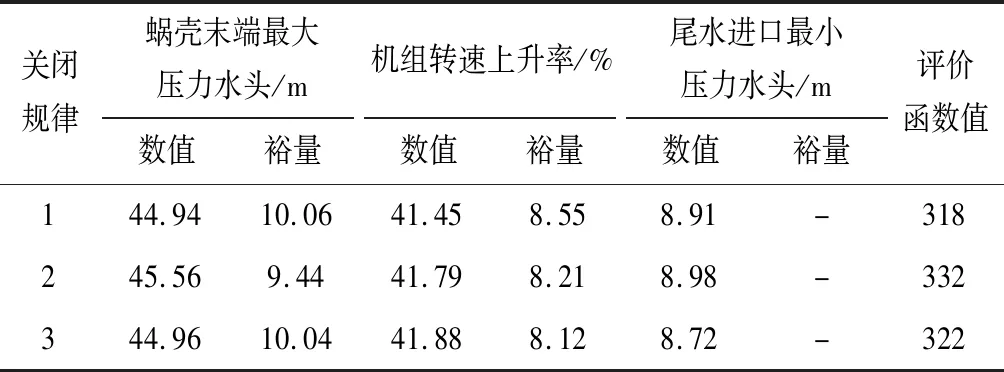
表2 不同关闭规律情况下的计算结果Tab.2 Calculation results under different closing laws
对比表2和表1可以看出,使用模拟退火算法优化得到的导叶-桨叶协联关闭规律,两个控制工况下的蜗壳末端最大压力与机组转速最大上升率均有明显下降,且安全裕量分配较为合理。从图10中可以看出,导叶快关造成的第一波水锤压力最大值和导叶慢关造成的第二波水锤压力最大值基本接近,进一步说明优化得到的关闭规律是合理的,能够将整个导叶关闭期间的蜗壳水锤压力控制的较为平均。
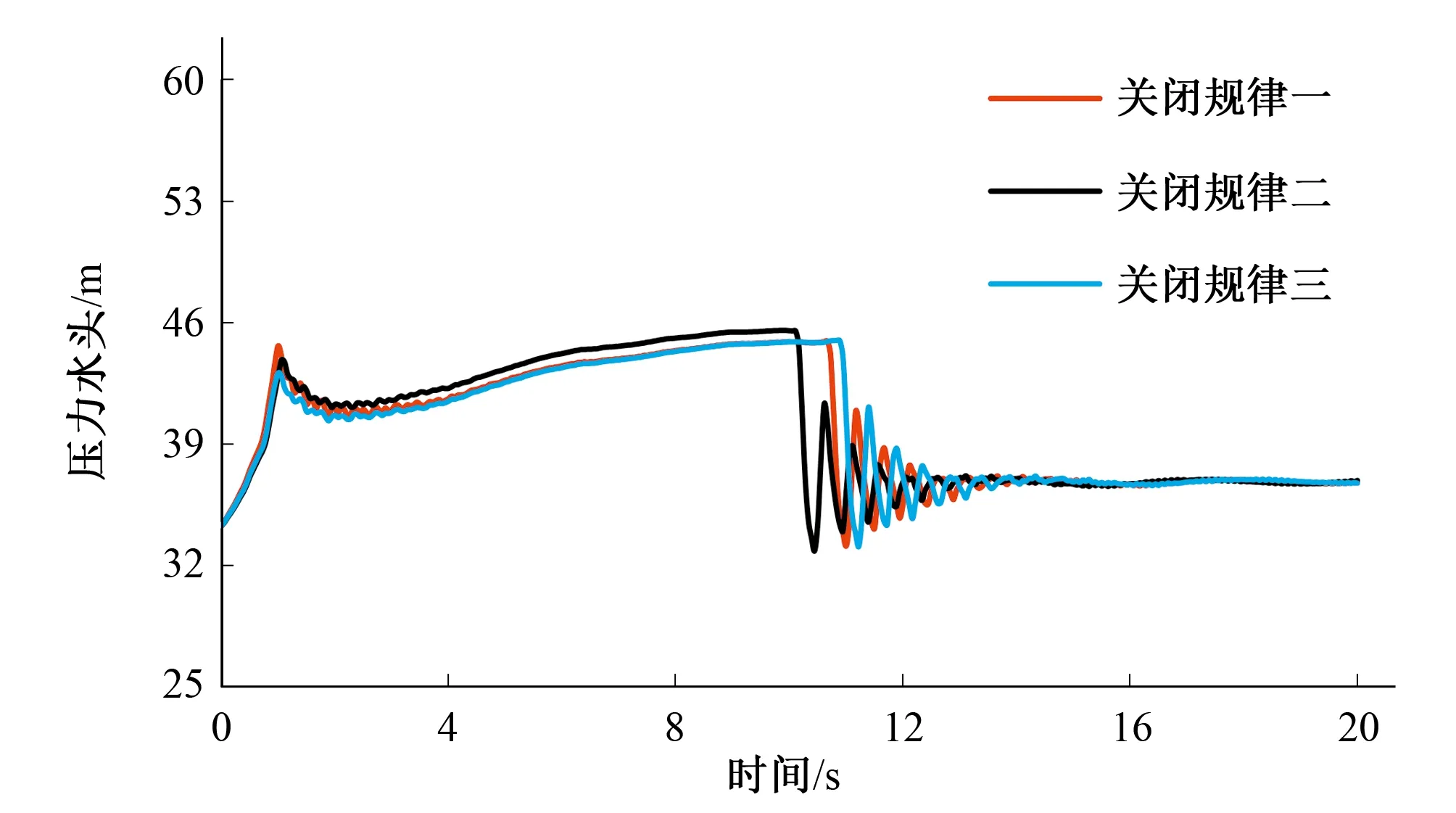
图10 蜗壳进口压力随时间变化图(工况一)Fig.10 Pressure change with time at the volute end (condition 1)
根据以上优化计算过程可以得到适合该轴流转桨式机组的甩负荷协联关闭规律,采用这种关闭规律,调保计算指标能够满足设计要求。
3 结 语
本文通过分析轴流转桨式水轮机飞逸曲线的特点,提出一种适合转桨式机组的协联关闭规律,并结合工程实例,采用数值模拟手段,证明了该关闭规律的可行性。最后,采用多工况非线性优化模型和模拟退火智能算法对提出的协联关闭规律进行优化,得到调节保证计算参数安全裕量分配较为合理协联关闭规律。结果表明:
(1)转桨式机组发生甩负荷时,桨叶开启、导叶关闭的协联动作方式可以大大降低机组转速最大上升率,而蜗壳末端压力会有略微上升,但上升幅度很小。
(2)通过非线性优化模型,采用模拟退火算法可以对新型协联关闭规律进行优化计算,优化结果能够很好地满足调节保证计算的控制要求,且安全裕量分配较为合理。
此外,本文提出此种关闭规律仅考虑了蜗壳末端最大压力、机组转速最大上升率以及尾水管进口最小压力三项调保计算指标,实际上,转桨式机组的轴向水推力问题也很重要,关于该关闭规律会对机组轴向水推力产生何种影响将会进一步研究。
□
