基于复杂网络的北京管制区航路网络特性分析*

任广建 朱金福 卢朝阳

(北京交通大学交通运输学院1) 北京 100044) (南京航空航天大学民航学院2) 南京 211106)

0 引 言

航路网中的主要元素有航路点和航路，每个元素都具有经纬度和高度特性.这里忽略各要素的空间特性，建立航路交通复杂网络模型，并用复杂网络理论对航路拓扑特性进行分析.

运输网络的不断发展构成了一类复杂网络体系.同时，国内外学者针对复杂网络理论在交通运输领域的应用也有居多研究.刘宏鲲等[1]分析了中国城市之间的航空运输数据，以城市为节点，节点之间航线为边建立了网络模型，结果表明，该网络具有小世界特性，其节点度服从幂律分布.Mo等[2]分析了中国航空运输网络的演化结构，为航空网络理论演化模型的设计提供了实验基础.Cai等[3-4]运用复杂网络理论分析中国航路网络，将航路模型与机场网络模型进行对比研究发现，中国航路网络的度分布、聚类系数、最短路径长度等特性明显不同于中国机场网络.党亚茹等[5]以七大空管区域网络为数据基础，建立复杂网络模型，研究了各个管制区域的复杂网络拓扑特性.徐良杰等[6]在分析中小城市的公交运行网络基础上,针对其缺陷提出了运行网络的改进措施.Du等[7]以中国省级行政区为单位建立中国省级航空运输网络，并分析其拓扑特性.同时，城市轨道交通网络作为一种典型的复杂交通运行网络也得到了深化研究[8-9].武喜萍等[10]以复杂网络理论为基础，分析了空中交通的复杂性，利用传播模型研究了航空延误传播规律.Dai等[11]统计分析了1979—2012年的东北南亚航空运行网络数据，并对其演化和结构特性进行了研究.王兴隆等[12]建立了一种包含机场网络、航路网络和管制网络的综合网络模型,并研究了各层网络的相关性.

基于此，文中在研究北京管制区航路网络基本数据的基础上，建立航路网络模型，并利用复杂网络理论对该模型进行分析，进而得出北京航路运行网络的拓扑特性.

1 航路网络特性参数

为了研究机场网路的特性，建立无向赋权机场网络模型，该网络表示为G=(V,E).其中：N为网络的节点数；E为网络的边集合.此外，其邻接矩阵为A={aij}.其中：aij=1时为节点i与节点j相连接；aij=0时两节点不相连.同时，该模型的加权邻接矩阵B={bij}，其定义为

(1)

式中：wij为节点i与节点j边上的权值.

1.1 度分布

网络中各节点度数具有差异性，各节点的度是服从一定概率分布的.这里P(k)为网络的度分布，它表示度为k的节点数占整个网络节点数的比率.同时，相应节点的累积度分布为

(2)

式中：Pk为度不小于k的概率分布.

1.2 度相关性

度相关性是网络的一个重要统计特征，它描述了网络中具有度大的节点与度小的节点之间的相关关系.对于节点i，其最近邻平均度值为

(3)

式中：ki为节点i的度；aij为邻接矩阵元素.

同时，具有度值k的节点的最近邻平均度值的平均值为

(4)

式中：P(k′/k)为度为k的节点与度为k′的节点邻接的条件概率.

1.3 Pearson度相关性系数

度-度相关性系数(Pearson相关系数)为节点度之间的相关性关系.边两端节点度的Pearson相关系数r为

(5)

式中：ki和kj分别为边eij两端节点的度；M为网络边的数量.该相关系数的范围为-1≤r≤1，当r>0时，网络为正相关，r<0时，网络为负相关，r=0表示网络不相关.

1.4 节点强度

点强度也称为点权是无权网络节点度的推广.节点i的点强度定义为

(6)

式中：Ni为节点i的邻居节点集合；wij为节点i和j之间边的权重.针对无向赋权网络，其节点强度为

(7)

式中：aij为邻接矩阵元素.

1.5 点强度相关性

对于无向赋权网络，其加权平均最近邻权为

(8)

式中：S为点强度.则具有点强度为S的所有节点，其加权平均近邻权的平均值为

(9)

式中：N为网络节点数量；P(s)为点强度分布函数.

1.6 聚类系数

聚类系数可以定量的反映复杂网络的集聚性，平均聚类系数表示在网络中和同一个节点连接的两个节点之间也互相相连的平均概率.设节点i与ki个节点相连，则这ki个节点之间存在的最大边数量为ki(ki-1)/2，其中实际有的边数为Mi，可得节点i的聚类系数为

(10)

式中：Ci为节点i的聚类系数；ki为节点i的节点度.

2 航路网络中心性度量

2.1 度中心性

度中心性是较简单的一种中心性测量方法.则节点i的度中心性为

(11)

式中：N为网络的节点总数.

2.2 紧密度中心性

紧密度中心性是基于节点i和节点j之间的最短路长度而计算的.一般情况下，当节点i与其它节点的平均最短路径长度较小时，该节点的紧密度中心性往往比较大.根据以上分析，节点i的紧密度中心性为

(12)

式中：dij为节点i和节点j之间的最短路长度.当网络中存在孤立的点时，运用式(12)难以准确的计算节点的紧密度，这时需要假设一个连通的网络来获得节点紧密度中心性.

对于不连通的网络，其节点紧密度中心性定义为

(13)

当两个节点不连通时，dij=∞，2-dij=0.

2.3 介数中心性

节点介数是一个全局性的复杂网络特征量，它反映节点在整个网络中的重要性.网络中不相邻的节点i和j之间的最短路会经过一些节点，当某个节点被许多最短路径经过时，该点就具有较大的影响力，其影响性或重要性用介数中心性表示.

对于节点i其介数中心性为

(14)

式中：σst为节点s和节点t之间的最短路径条数；σst(i)为节点s和节点t之间的最短路径中过节点i的条数.

2.4 特征向量中心性

特征向量中心性是节点重要性指标之一.通过特征向量网络中每个都得到一个相对的得分，对于每个节点分值的贡献来说，高分值节点的连接数比低分值节点的连接数多.基于网络邻接矩阵，节点i的特征向量中心性为

(15)

式中：λm为网络邻接矩阵A的最大特征值，e=[e1,e2,…,eN]T为相应的特征向量；aij为邻接矩阵A中的元素.

3 航路网络模型

3.1 北京管制区航路网络数据

北京管制区是中国最繁忙的航空区域之一，因此其特性研究具有代表性和典型性.航路网路是空中航空器运行的载体，它构成了空域的基本骨架.其中，航路点(导航点)是构成航路的主要因素之一，同时航路点可以引导航空器的运行航迹；航路点之间具有一定宽度的空域是具体运行航路，它们构成了航空器空中运行轨迹.通过对中国空中交通管理局的数据统计分析可知，北京区域航路网络主要航路点有约69个，航路254条.

3.2 航路网络模型建立

基于以上对北京区域航路网络数据的分析，本节从复杂网络理论的角度建立航路网络复杂网络模型.具体模型构建过程如下.

1) 假设各航路点无高度差异，航路点构成网络模型的节点，当两个节点之间有航路联系时，则加上一条边.

2) 两个航路点之间可能存在多条航路，多条航路缩减为一条边.

3) 该航路网络模型为双向赋权网络，各边是双向的，且节点之间的平均日航班量为边的权重.

通过以上分析，北京管制区航路复杂网络模型见图1.

图1 北京区域航路网络模型

图1中，实心圆圈为航路模型的节点，节点间实线是该网络的边.各个航路点通过航路相互联系，相互影响构成了一个复杂网络系统.根据复杂网络理论，北京区域航路网络模型的基本拓扑特性见表1.

表1 北京航路网络模型基本参数

由表1可知，北京区域航路网络的节点数为69，边数为254，因此，可知该网络的密度约为0.11，与完全网络(密度为1)有一定差距,该网络比较稀疏，还有较大的发展空间.平均度为3.68，说明北京管制空域中每个航路点平均与4个航路点通过航路相联系.该模型的系数为0.17，同时平均最短路径为3.69，这一定程度上反映出，该网络具有小世界网络的一些特性.

4 航路网络拓扑特性分析

拓扑是复杂网络系统最重要的特征之一.航路网络系统可以简化为复杂网络模型，分析北京航路网络的拓扑特征，结果见图2.

图2 北京管制区航路网络拓扑特性分析图

由图2a)可知，北京航路网络节点度最大值为11，最小值为1，平均度值为3.68.同时，北京航路网络模型节点度分布呈现两个阶段，第一阶段度分布下降较为缓慢，且集中于平均度之前，这时累积度分布到达55%.第二阶段，当节点度值大于平均度时，节点度值下降较快，这时累积度分布为45%.总体上，该模型累积度分布服从双段幂律分布，因此北京航路网络接近于无标度网络且在一定程度上具有非均匀网络的特性.

由图2b)可知，该模型节点强度服从指数分布规律.因此，北京管制区航路点之间的流量分布不均衡，流量集中现象比较明显；这也反映出空域中局部的流量拥挤情况.为了减少航班延误，应重点关注流量集中的航路区域，采取措施降低相关区域的管制压力，提高运行效率.由图3c)可知，北京航路网络模型中，节点度与其邻居节点平均度呈现负相关关系这说明度大的节点倾向于和度小的节点相连.同时，度相关系数r为负数，因此该航路网络具有异配特性.由图3d)可知，北京航路网络中节点强度与其邻居节点平均强度呈现正相关关系.由此，该航路网络中流量强度大的航路点一般和流量大的航路点进行相互联系.也就是说，流量具有一定集聚效应，交通压力大的航路点，其周围邻居节点的交通压力也较大.

5 度与中心性统计量关系

统计分析北京航路网络的节点度与介数、紧密度、向量中心性和节点强度的关系，描述网络中各航路点的中心特性，见图3.

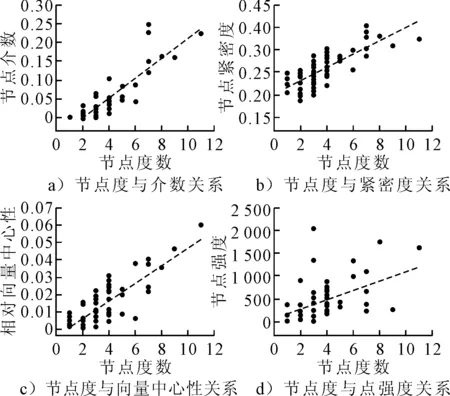
图3 节点度与介数，紧密度，向量中心性和节点强度的关系

由图3a)可知，北京航路网络中节点度与介数具有较高的相关性，且表现为正相关关系.度大的航路点在网络中其介数也比较大，这说明，一般情况下在整个北京区域航路网络中，航路连接较多的航路点，其枢纽中心性也较大.在实际管制运行中，度大的节点也往往是运行压力大的航路点，因此要加强相关航路点的空中管制.

由图3b)可知，节点度大的航路点，倾向于具有较大的紧密度，由此，北京航路网络中具有节点度大的航路点在空域运行中具有重要影响力.

由图3c)可知，节点度与特征向量中心性具有正相关关系.特征向量中心性反映了航路点之间的相互影响，即，航路点的重要性不仅与其所连接的边数有关，还与其相连接的邻居节点的重要性有关；特性向量中心性高的航路点其直接相连的航路点往往也比较重要.

航路网络中，航路流量的集中性由点强度来表示.由图3d)可知，节点度与点强度的关系，可知两者有明显的正相关性，但同时，两者之间的关系波动也较大.该航路网络中存在节点度较小，而具有较大流量强度的航路点.总体上，具有较大节点度航路点，同时，也具有较大的流量强度.

总之，该航路模型中，各个航路点中心性度量值具有一致的正相关性.实际运行中，度大的航路点不仅是航路交汇较多的点，也是整个航路网络中交通流量相对集中的区域(即枢纽性航路点).因此，在进行空中交通管制时应重点调控节点度较大的航路点，适时分流，从而优化空中运行态势，提高航路运行效率.

6 结 束 语

文中以北京管制区航路网络数据为基础，通过对数据的分析建立航路复杂网络模型，然后根据复杂网络理论分析该航路网络的拓扑特性.该模型是赋权复杂网络，其节点为空域中的航路点(导航点)，节点之间的航路为网络的边，边的权重为日平均航班流量.结果表明，北京区域航路网络具有一定的小世界特性，同时该模型为异配性网络.此外，航路间的航班流分布具有非均匀性，局部流量有明显的集中现象.航路点的度值与介数、紧密度、特征向量中心值以及点流量强度具有明显的正相关关系，这说明该航路网络中，航路点的重要性具有相对的一致性，度大的点同时也具有较大的其他中心性度量值，同时，结构上处于中心性的航路点也是航空交通流比较集中的区域.利用复杂网络理论来分析航路网络可以较好反映航路中各元素的特性，并且能较为形象的解释航路的整体结构分布.