基于Laplace先验和稀疏块相关性的旋转机械振动信号贝叶斯压缩重构
2021-03-05马云飞白华军温亮郭驰名贾希胜
马云飞, 白华军, 温亮, 郭驰名, 贾希胜
(1.武警士官学校 军械系, 浙江 杭州 310023; 2.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003)
0 引言
为了实时监控装备运行状态,利用分布式无线传感技术实现机械信号传输、监测,具有一定的应用价值和发展潜力。相对于有线的故障预测与健康管理系统,无线监测系统能够大大增加灵活性、可维护性和可扩展性[1]。而受无线传输带宽限制,想要实时监控必须对信号进行压缩传输。此前,有学者对结构健康监测领域的振动信号压缩进行了研究[2-3],但在该领域中进行振动信号监测的采样频率较低,信号压缩实现相对较为容易。例如在桥梁结构监测中仅需要240 Hz的采样频率[4],而要想实现机械振动信号监测,则至少需要5~20 kHz的采样频率[5]。由于机械振动信号具有非平稳、非线性等特征,且设备运转过程中会产生大量噪音,给信号压缩带来极大困难。
压缩感知(CS)理论[6-8]近年来引起学者广泛关注,其基本原理是利用与压缩信号线性无关的观测矩阵对稀疏信号进行采样,降低采样信号维数,并在接收端利用重构算法估计原始信号。目前,基于CS的重构算法可以归为三类:凸优化算法[9]、贪婪算法[10]、贝叶斯CS(BCS)算法[11]。BCS算法将贝叶斯估计原理与CS结合,利用稀疏贝叶斯模型中的相关向量机(RVM)[12]学习估计原始信号的最大后验概率。BCS算法的优点是充分考虑了信号传输中产生的噪音,且并不要求原始信号符合稀疏的性质。此外,Babacan等[13]在BCS框架下,利用Laplace先验代替高斯先验约束未知信号,该先验能够在对数凹时最大程度地消除局部极小值,从而优选接近于零的信号系数。Ji等[14]将单任务BCS扩展为多任务BCS,通过挖掘多任务之间稀疏信号的统计相关性来实现多个稀疏信号联合重构。
对机械振动信号CS,文献[15]提出对变分模态分解分量进行CS,并通过循环模式矩阵定义新的观测矩阵;文献[16]将以往频域稀疏化方法改为相空间稀疏化,并利用主成分分析提取特征,更有效促进信号稀疏性;文献[17]利用改进m序列原理设计观测矩阵电路实现,并通过滚珠丝杠动态测试中的振动信号验证了系统可行性。尽管上述研究取得了较好的效果,但是已有文献缺乏机械振动信号的BCS相关研究,且没有考虑到机械信号的内部相关性。
本文提出一种基于Laplace先验和稀疏块相关性的BCS(Lap-CBCS)算法。由于Laplace先验具有更好的稀疏促进作用,特别适合于机械振动信号这一类复杂信号。建立基于该先验的多任务BCS框架,并通过对模型中各信号块共享的超参数进行估计,实现信号重构。改进算法充分利用Laplace先验的稀疏促进作用和类周期信号的内部相关性,以提高重构的准确性,为机械设备无线状态监测提供技术支撑。
1 CS与贝叶斯重构
1.1 CS原理
CS[8]利用一个低维信号近似表达原始信号。假设原始信号为x(x∈RN,N为原始信号长度),稀疏变换为Ψ,观测矩阵Φ∈RM×N(M≪N,M为观测矩阵行数或称观测次数)。则信号x在该矩阵上的线性投影y∈RM可以作为压缩信号,
y=Φx=ΦΨθ=Θθ,
(1)
式中:θ表示稀疏信号;Θ为传感矩阵,Θ=ΦΨ.
由此,给出压缩率定义:
(2)
由(2)式可知,原始信号越长,观测次数越小,则压缩率越高,也越难实现精确重构。在y和Θ已知情况下,求解θ,可根据信号的稀疏性质,将信号重构问题转化为0-范数最优化问题,即
min ‖θ‖0,
s.t.y=Θθ=ΦΨx.
(3)
该问题可利用基追踪(BP)算法[8]、正交匹配追踪(OMP)算法[10]求解。
1.2 贝叶斯重构
1.2.1 问题转化
BCS算法[11]从概率角度出发,求解原始信号的最大后验估计值,以恢复信号。令θs表示保留θ的M个最大分量、剩余分量置0的向量,θe表示保留剩余N-M个分量、其余分量置0的向量,则y可拆分成
y=Θθ=Θθs+Θθe=Θθs+ne,
(4)
式中:ne表示信号次要信息。
信号y传输过程中,可能存在噪音nm,则y表示为
y=Θθs+ne+nm=Θθs+n,
(5)
式中:n表示方差为σ2的零均值高斯噪声。
1.2.2 构造先验分布
构造y关于参数θs和σ2的先验密度函数:
(6)
RVM[12]是一个通用的贝叶斯框架,该框架使用参数中的线性模型来获得回归和分类任务的稀疏解。传统模型采用分层先验模型,并假设θs的先验分布为高斯分布。与该分布相比,Laplace先验通过在轴上更多地使用后验分布来严格约束稀疏性,因此信号系数更接近于0,本文假设其服从Laplace分布。
1.2.3 参数迭代求解
在RVM框架下如果y和超参数的先验分布已知,可以得到θs的均值和方差表达式。进一步,令超参数的边缘分布最大,利用极大似然估计得到超参数更新表达式。通过反复迭代可估算出所有参数值,最后用θs的均值估计表示θs.
2 Laplace先验和稀疏块相关的BCS
2.1 基于Laplace分布的贝叶斯先验模型
在BCS领域应用较多的是估计值服从高斯先验的模型。研究表明,在实数域应用高斯分布和指数分布共轭的Laplace先验模型比高斯先验具有更好的稀疏促进作用[13]。由于机械振动信号也是实数信号,可以用Laplace先验约束。假设振动信号θs服从Laplace先验,参数集γ=[γ1,γ2,…,γj,…,γN]。如图1所示,Laplace分布可表示为高斯分布和指数分布的混合形式,结合对超参数γj的指数约束,得到θs关于λ的Laplace分布表达式为

图1 Laplace贝叶斯分级先验模型Fig.1 Laplace priors-based architectural model
(7)
式中:λ为Laplace模型中描述γj的超参数;p(θs|γ)表示θs关于γ的先验分布;p(γ|λ)表示γ关于λ的先验分布;p(θs|λ)表示分层先验分布。
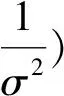
有关噪声n的超参数α0=1/σ2仍服从Gamma分布。若给定γ、λ和σ2,则在已知观测值y下的后验概率分布可表示为p(θs,γ,λ,σ2|y)=p(θs|y,γ,λ,σ2)p(γ,λ,σ2|y)。其中p(θs|y,γ,λ,σ2)服从关于均值为μ、协方差为Σ的高斯分布,且有
μ=σ-2ΣΘTy,
(8)
Σ=(σ-2ΘTΘ+Λn-λ)-1,
(9)
式中:μ为θs的均值;Σ为θs的方差;Λn-λ=diag(1/γ1, 1/γ2,…,1/γj,…,1/γN)=diag{1/γj},该矩阵的估计依赖于超参数λ.由于p(γ,λ,σ2|y)∝p(γ,λ,σ2,y),求p(γ,λ,σ2,y)的解析式如下:

(10)
式中:p(y|θs,σ2)为y关于参数θs和σ2的先验密度函数;p(θs|γ)为θs关于参数γ的先验密度函数;p(γ|λ)为γ关于超参数λ的先验密度函数;p(λ|v)为λ关于超参数v的先验密度函数;p(σ-2)为σ2的先验分布函数。
(10)式取对数并略去常数项后,分别对其求γj、λ、σ2偏导并令偏导等于0,根据超参数为正且v=0,解得γj的更新公式为

(11)

2.2 对多稀疏块的Laplace BCS

(12)

(13)
λn=2(N-1)/(Σjrj),
(14)
式中:μi,j表示第i块数据中第j个参数γj的估计均值;Σi,jj表示第i块数据的方差Σi的第j个对角线元素,其表达式见(9)式。利用(13)式、(14)式迭代计算复杂度较高,本文采用文献[14]的快速RVM算法。
3 基于Lap-CBCS算法的机械振动信号压缩重构
类似于机器学习中每次训练样本都会对模型参数进行优化,对于多数据块的压缩重构也是如此。Lap-CBCS算法参考多任务贝叶斯估计,将多块数据看作多任务贝叶斯中的任务,构建稀疏块Laplace先验分布模型,使得每块数据都能够对先验分布参数进行改进,就可以促进各块的稀疏重构,大大提高贝叶斯参数估计的准确性。但想要将Lap-CBCS算法应用到实际机械振动信号的压缩重构中,还需要解决信号分块和稀疏域选取两个问题。
3.1 机械振动信号的周期性分块
由于齿轮箱振动信号具有非线性、非平稳性,其周期性表现得并不明显,可称其为类周期性。机械振动信号的类周期确定主要有如下3种方法:
1)根据转速和采样频率计算类周期。假设转速n=600 r/min,采样频率Fs=5 kHz,即采样点数为5 000个/s,周期T=Fs/n=5 000/10=500个,由此可得每500个采样点为一个类周期。
2)通过频谱分析确定。可以利用傅里叶变换得到信号频谱图,分析信号频谱图,得出信号类周期。
3)通过包络线确定。首先对信号作自相关分析,并求得自相关信号包络线。然后取包络线上相邻两峰值之间的距离作为类周期。
对机械振动信号进行傅里叶变换后会出现大量的频谱峰值,难以识别类周期。而通过求包络线计算误差也较大,还需要对多个候选值求平均。因此,本文采用通过转速和采样频率计算类周期的方法,转速信息可通过转速传感器测得。
3.2 稀疏域选取
常见稀疏变换方法有离散余弦变换、小波变换等,稀疏域选取可根据信号稀疏度和相似度确定。
定义1稀疏度。假设原始信号x(x∈RN)在某变换域Ψ上是稀疏的,则稀疏信号θ与原始信号关系为x=Ψθ,变换后信号的0-范式‖Ψ-1x‖0,且Ψ-1x∈RM,则稀疏度可表示为K=‖Ψ-1x‖0/M.
定义2相似度。假设函数R(s,t)={δ|如果|si-ti|>ε则δi=1,否则δi=0,i=0,1,2,…,N},其中ε为阈值,则两组信号x1,x2∈RN的相似度可表示为D=1-‖R(Ψ-1x1,Ψ-1x2)‖0/M.
3.3 机械振动信号压缩重构流程
本文提出了基于Laplace先验和稀疏块相关性的机械振动信号压缩重构方法(见图2),具体包括以下步骤:

图2 基于Laplace-CBCS算法的机械振动信号压缩重构流程Fig.2 Compression and reconstruction processes of mechanical vibration signal based on Laplace-CBCS algorithm
步骤1周期性分块。根据类周期对采集到的振动信号进行周期性分块。利用转速n和采样频率Fs计算类周期,计算公式为T=Fs/n.
步骤2信号压缩。由于机械振动信号是一类非平稳复杂信号,为了提高其稀疏度,首先利用稀疏基Ψ将该信号投影到稀疏域,令原始信号x=Ψθ,得到稀疏域信号θ.利用传感矩阵Θ=ΦΨ对稀疏信号进行状态压缩,得到压缩后信号y=Θθ.
步骤3信号分块传输。分别传输并接收分块处理后的信号y1,…,yL.
步骤4x信号重构。利用本文Lap-CBCS重构算法以及从前端采集节点传回的传感矩阵Θ1,…,ΘL(如果观测矩阵是确定性矩阵则无需传回,如果是随机性矩阵则需要传回)对y1,…,yL联合重构,得到稀疏信号θ1,…,θL.对稀疏信号进行逆稀疏变换,得到原始分块信号x1,…,xL,将原始信号块按顺序拼接在一起,得到完整重构信号x′.重构信号与原始信号相比相位不发生变化。
4 齿轮箱数据实验验证
4.1 实验准备
如图3所示,实验齿轮箱型号为JZQ175,三相电磁调速电动机功率4 kW,风冷磁粉制动器为齿轮箱提供载荷。数据采集由美国DYTRAN公司生产的4个3056B4型压电传感器组成。利用上述设备进行齿轮箱预制故障实验,转速800 r/min,输入端负载10 N·m,采样频率20 kHz,采样时间为6 s. 将上述实验环境下采集到的数据进行信号压缩、传输,重构仿真实验。仿真环境为:MATLAB 2017b,Win10操作系统,i5-8250 CPU.

图3 实验台示意图Fig.3 Test-rig of gearbox
预置故障实验主要包括两种:齿根裂纹故障实验和断齿故障实验。齿根裂纹故障加工在输出轴大齿轮齿根上,断齿故障加工在中间轴大齿轮上。本文进行4种预置故障实验:正常状态、1 mm齿根裂纹故障、2 mm齿轮断齿故障、2 mm齿根裂纹故障(1 mm、2 mm表示裂纹深度),采样时间为6 s,采样点数120 000,采集到的数据如图4所示。
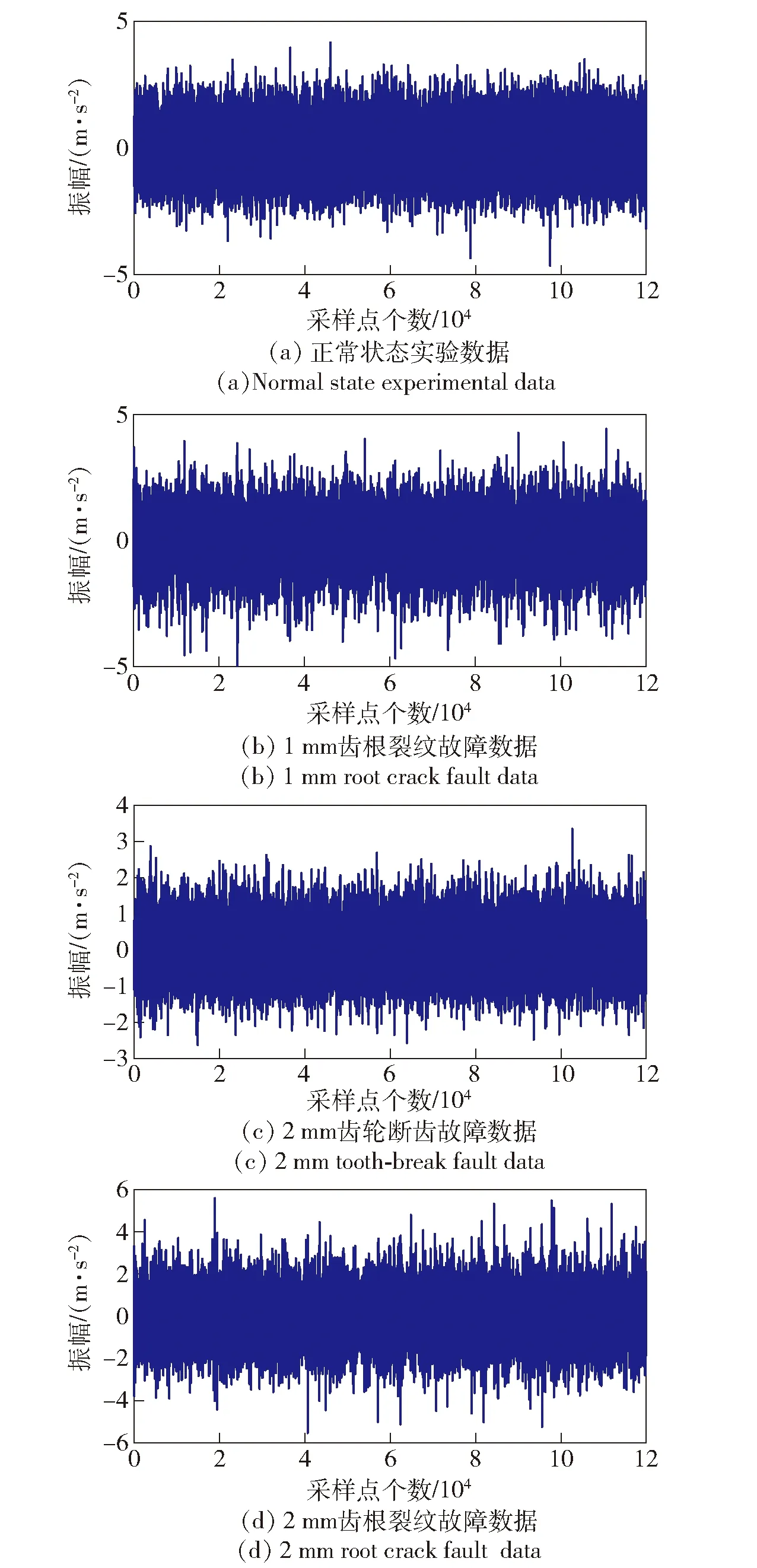
图4 齿轮箱实测振动信号Fig.4 Measured vibration signals of gearbox
4.2 1 mm齿根裂纹故障仿真实验
4.2.1 根据转速和采样频率计算类周期
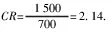
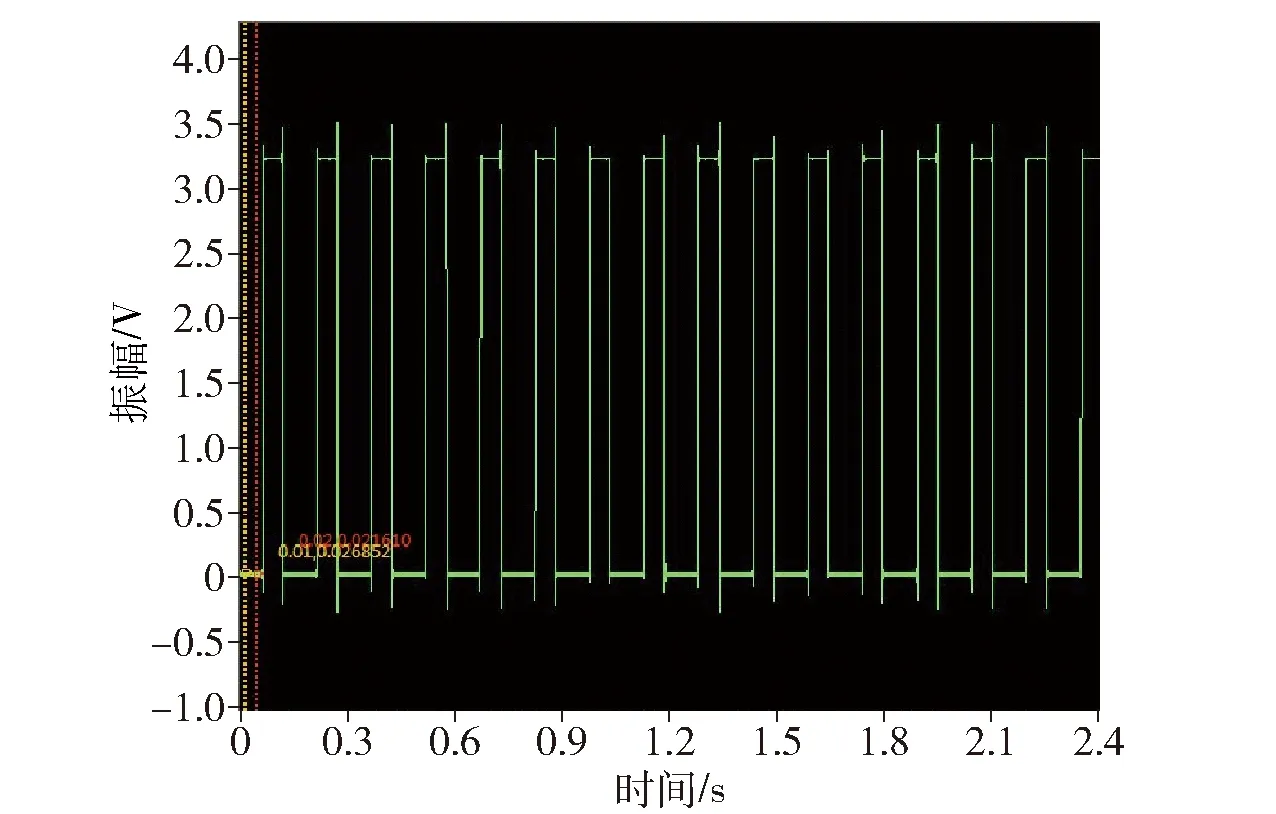
图5 转速信号Fig.5 Tachometer signal
4.2.2 稀疏域选择
针对实测数据,分析离散余弦变换以及小波变换处理后稀疏信号的稀疏度与相似度。观察处理数据发现,小波分解层数对于变换后信号的稀疏性、相似性影响都不大。而对于稀疏信号,稀疏度越小,相似度越高,越容易进行信号恢复。仿真实验结果表明:离散余弦变换作为稀疏变换的处理效果是最好的。
4.2.3 利用Lap-CBCS算法对1 mm齿根裂纹故障数据进行仿真实验
为对比分析,先利用BCS算法对80块信号分别压缩重构,再利用Lap-CBCS算法对80块信号联合压缩重构,对比两次重构。此外,本文拟采用标准均方根误差(MSE)作为重构效果评价指标,其计算公式如(15)式所示:
MSE=‖u-u′‖2/‖u‖2,
(15)
式中:u表示原始信号;u′表示重构信号。
如图6所示,随机选取第1、15、22、36、61块数据进行比较分析,发现BCS方法对每块信号单独压缩重构MSE大于0.8,而利用Lap-CBCS算法重构可将MSE降低到0.3左右。

图6 实测齿轮箱1 mm裂纹数据压缩重构效果对比(80块信号联合重构)Fig.6 Comparison results of reconstructing signal blocks for measured 1 mm crack on root of tooth (simultaneous construction of 80 signal blocks)
将Lap-CBCS算法重构的80块信号拼接起来,可以得到完整重构信号。由于实验采样点数较多,无法看出重构细节,选择采样点1×104~2×104的数据观察细节。如图7所示,Lap-CBCS重构数据点基本能够覆盖原数据点。在该范围内,进一步选择出1.1×104~1.2×104的数据观察,发现Lap-CBCS算法重构只有在局部极值点处与原数据略有偏差,其余数据点基本重构成功。

图7 实测齿轮箱1 mm裂纹局部数据重构细节Fig.7 Details of local data reconstruction for measured 1 mm crack
4.2.4 与其他算法对比
本文利用BP、OMP算法针对上述齿轮箱1 mm齿根裂纹故障数据进行重构实验。实验结果表明BP、OMP、BCS算法的标准MSE都在0.5以上,而Lap-CBCS算法的MSE能保持在0.3左右。此外,分析4种算法运行时间发现OMP算法所需时间最少,其次是BP算法,而Lap-CBCS算法运行时间最长。
4.3 齿轮不同故障状态实验
选取另外3种状态:正常运行、2 mm齿轮断齿故障、2 mm齿根裂纹故障下的实验数据,由于转速和采样频率不变,分块周期仍为1 500数据点。对每种状态数据分别利用BCS、Lap-CBCS、BP、OMP 4种算法进行压缩重构分析。
选取观测次数400、700、1 000(对应压缩率3.75、2.14、1.50),对每种不同状态数据计算出MSE和运行时间平均值,得到表1所示结果。
由表1可见4种算法的标准MSE存在如下关系:MSELap-CBCS 表1 不同齿轮箱状态下重构算法MSE与运行时间对比Tab.1 Calculated MSEs and running times of different algorithms under different gearbox conditions 1)随着压缩率降低,CS算法MSE降低,且算法运行时间增加。其中MSELap-CBCS最低,在压缩率为2.14和1.5时可基本实现重构(MSE不大于0.3),而BP、BCS算法只有在压缩率1.5时才能实现重构(齿根裂纹故障状态下仍不能实现重构)。另外,如果使用OMP算法则MSEOMP较大,表明该算法对于复杂机械振动信号这类非稀疏信号较为敏感,不适用于复杂齿轮箱数据的重构。 2)Lap-CBCS算法运行时间较长,对计算资源要求高。尽管如此,考虑到振动信号传输到上位机后后台可利用的计算资源较多,且在某些特定场景下需要高精度的信号重构技术,因此Lap-CBCS算法具有较好的应用价值。 本文将Laplace先验模型和振动信号周期性稀疏块相结合,提出一种改进的BCS方法。针对机械振动信号,提出利用转速和采样频率计算类周期进行周期性分块,并给出振动信号压缩重构流程。所得主要结论如下: 1)齿轮箱实测信号验证结果表明,尽管Lap-CBCS运行时间较长,但在标准MSE方面优于BCS、BP、OMP 3种典型算法。 2)Lap-CBCS方法较好地解决了复杂非平稳信号的压缩重构问题,对于机械设备的无线监测具有一定的促进意义。 但是,Lap-CBCS算法虽然重构精度较高,却需要较长的运行时间。如何改进算法、提高计算效率,将是下一步可能的研究方向。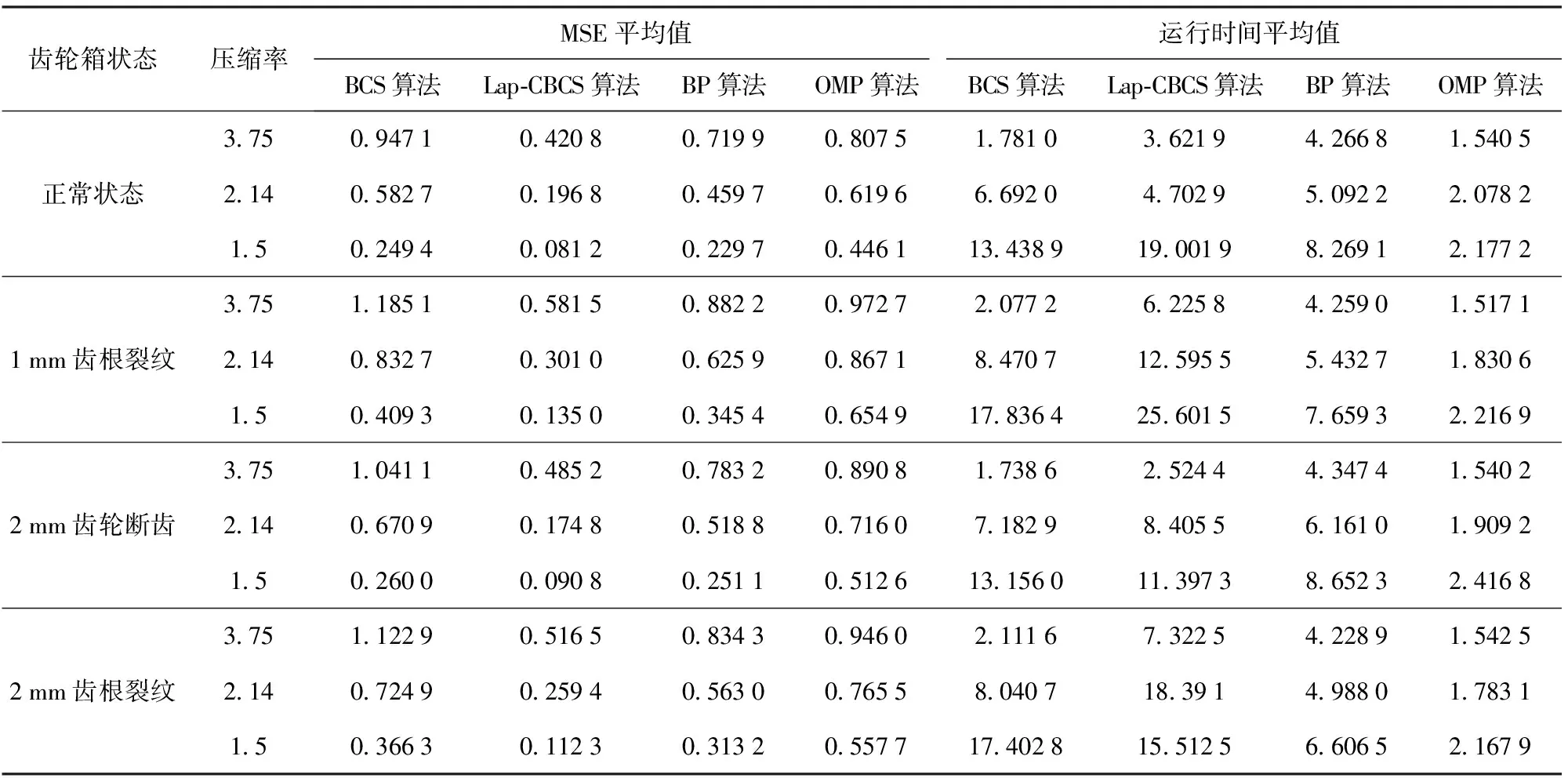
5 结论
